选择性必修第二册苏教版第8章单元测试卷(含解析)
文档属性
| 名称 | 选择性必修第二册苏教版第8章单元测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 109.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-07 11:07:28 | ||
图片预览




文档简介
第8章 概率 单元测试卷
附:若随机变量X服从正态分布N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.683,P(μ-2σ≤X≤μ+2σ)≈0.954,P(μ-3σ≤X≤μ+3σ)≈0.997.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知离散型随机变量ξ的分布列为则均值E(ξ)等于 ( )
ξ 1 3 5
P 0.5 m 0.2
A.1 B.0.6 C.2+3m D.2.4
2.设随机变量ξ服从正态分布N(1,4),则P(ξ<3)的值约为 ( )
A.0.173 7 B.0.347 4 C.0.683 7 D.0.841 5
3.甲、乙两人参加青年志愿者的选拔,选拔以现场答题的方式进行.已知在备选的10道试题中,甲能答对其中的6道题,乙能答对其中的8道题.规定每次考试都从备选题中随机抽出3道题进行测试,设甲答对的试题数为X,则X=2的概率为 ( )
A. B. C. D.
4.小林从A地出发去往B地,1小时内到达的概率为0.4,1小时10分到达的概率为0.3,1小时20分到达的概率为0.3.现规定1小时内到达的奖励为200元,若超过1小时到达,则每超过1分钟奖励少2元.设小林最后获得的奖励为X元,则E(X)= ( )
A.176 B.182 C.184 D.186
5.随机变量X的分布列如表所示,若E(X)=,则D(3X-2)= ( )
X -1 0 1
P A B
A.3 B. C.5 D.9
6.若随机变量X~B(3,p),Y~N(2,σ2),若P(X≥1)=0.657,P(04)= ( )
A.0.2 B.0.3 C.0.7 D.0.8
7.长时间玩手机可能影响视力,据调查,某校学生大约30%的人近视,而该校大约有40%的学生每天玩手机超过2 h,这些人的近视率约为60%.现从每天玩手机不超过2 h的学生中任意调查一名学生,则他近视的概率为 ( )
A. B. C. D.
8.体育课的排球发球项目考试的规则是:每位学生最多可发球3次,一旦发球成功,则停止发球,否则一直发到3次为止.设学生一次发球成功的概率为p(p≠0),发球次数为X,若X的数学期望E(X)>1.75,则p的取值范围是 ( )
A.(0,) B.(,1) C.(0,) D.(,1)
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列说法正确的是 ( )
A.设随机变量X服从二项分布B(6,),则P(X=2)=
B.设离散型随机变量X等可能取1,2,3,…,n,若P(X<4)=0.3,则n=10
C.设离散型随机变量η服从两点分布,若P(η=1)=2P(η=0),则P(η=0)=
D.设随机变量x服从正态分布N(2,σ2)且P(X<4)=0.9,则P(010.某计算机程序每运行一次都随机出现一个五位二进制数A=a1a2a3a4a5,其中A的各数位中ak(k=2,3,4,5)出现0的概率为,出现1的概率为,记X=a2+a3+a4+a5,则当程序运行一次时 ( )
A.X服从两点分布 B.X服从二项分布
C.X的均值E(X)= D.X的方差D(X)=
11.已知随机变量X的取值为不大于n(n∈N*)的非负整数,它的概率分布列为:
X 0 1 2 3 … n
P p0 p1 p2 p3 … pn
其中pi(i=0,1,2,3,…,n)满足pi∈[0,1],且p0+p1+p2+…+pn=1.定义由X生成的函数f(x)=p0+p1x+p2x2+p3x3+…+pixi+…+pnxn,g(x)为函数f(x)的导函数,E(X)为随机变量X的期望.现有一枚质地均匀的正四面体骰子,四个面的点数分别为1,2,3,4,将这枚骰子连续抛掷两次,记向下点数之和为X,此时由X生成的函数为f1(x),则 ( )
A.E(X)=g(2) B.f1(2)= C.E(X)=g(1) D.f1(2)=
三、填空题:本题共3小题,每小题5分,共15分.
12.由1,2组成的有重复数字的三位数中,若用A表示事件“十位数字为1”,用B表示事件“百位数字为1”,则P(A|B)= .
13.一个病人服用某种新药后被治愈的概率为0.9,则服用这种新药的4个病人中至少3人被治愈的概率为_________.(用数字作答)
14.某高校进行招生面试,评分规则是:共设3道题,每道题答对给20分、答错倒扣10分(每道题都必须回答,但相互不影响).设某学生每道题答对的概率都为,则该学生在面试时恰好答对2道题的概率是 ,该学生在面试时得分的期望值为 分.(本题第一空2分,第二空3分)
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)某班包括男生甲和女生乙在内共有6名班干部,其中男生4人,女生2人,从中任选3人参加义务劳动.
(1)求男生甲或女生乙被选中的概率;
(2)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(A)和P(A|B).
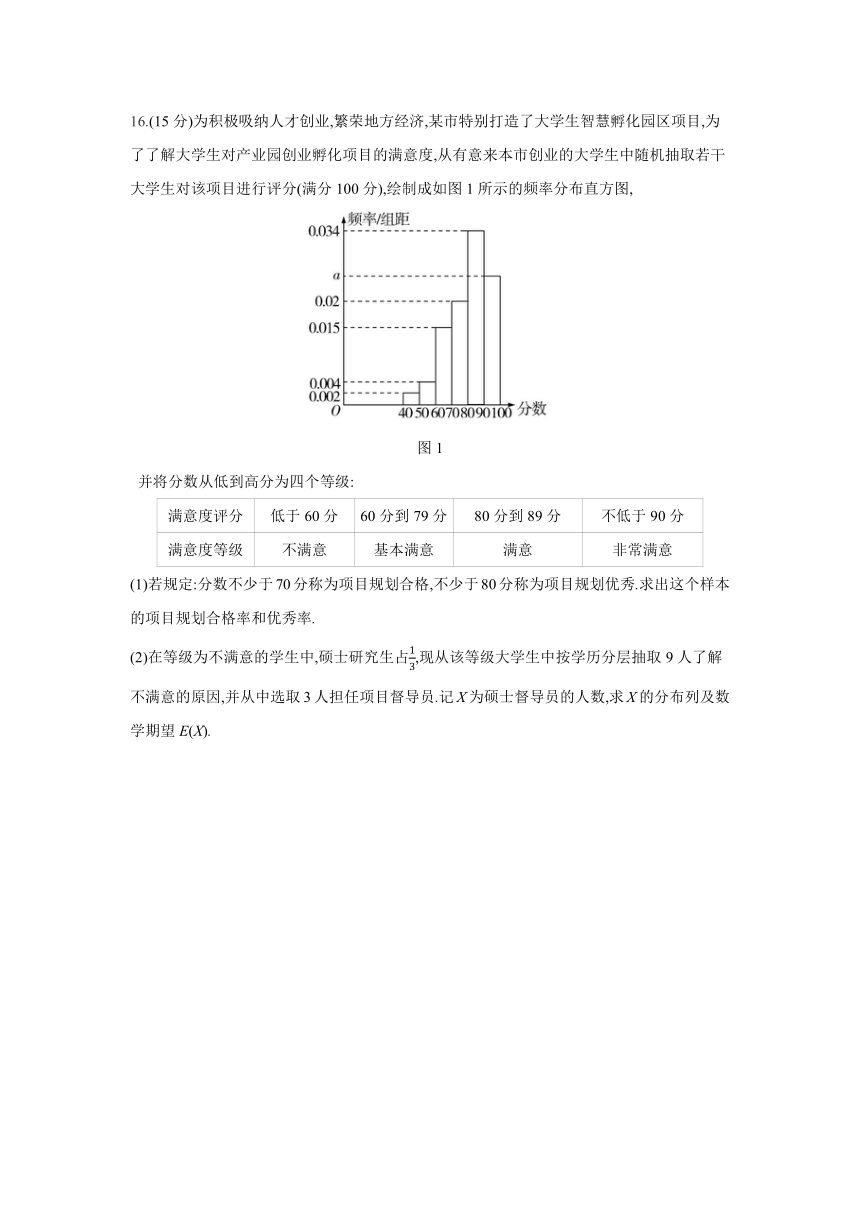
16.(15分)为积极吸纳人才创业,繁荣地方经济,某市特别打造了大学生智慧孵化园区项目,为了了解大学生对产业园创业孵化项目的满意度,从有意来本市创业的大学生中随机抽取若干大学生对该项目进行评分(满分100分),绘制成如图1所示的频率分布直方图,
图1
并将分数从低到高分为四个等级:
满意度评分 低于60分 60分到79分 80分到89分 不低于90分
满意度等级 不满意 基本满意 满意 非常满意
(1)若规定:分数不少于70分称为项目规划合格,不少于80分称为项目规划优秀.求出这个样本的项目规划合格率和优秀率.
(2)在等级为不满意的学生中,硕士研究生占,现从该等级大学生中按学历分层抽取9人了解不满意的原因,并从中选取3人担任项目督导员.记X为硕士督导员的人数,求X的分布列及数学期望E(X).
17.(15分)为了评估某大米包装生产设备的性能,从该设备包装的大米中随机抽取100袋作为样本,称其质量为
质量/kg 9.5 9.6 9.7 9.8 9.9 10.0 10.1 10.2 10.3 10.4 10.5 10.6 10.7 10.8 合计
袋数 1 1 3 5 6 19 34 18 3 4 2 1 2 1 100
经计算:样本的平均值μ≈10.10,标准差σ≈0.21.
(1)为评判该生产线的性能,从该生产线中任意抽取一袋,设其质量为X(单位:kg),并根据以下不等式进行评判.
①P(μ-σ②P(μ-2σ③P(μ-3σ若同时满足三个不等式,则生产设备为甲级;满足其中两个,则为乙级;仅满足其中一个,则为丙级;若全不满足,则为丁级.请判断该设备的等级.
(2)将质量小于或等于μ-2σ与质量大于μ+2σ的产品的包装认为是不合格的包装,从生产线上随机抽取5袋大米,求其中不合格包装袋数Y的均值E(Y).
18.(17分)如图2,李先生家住H小区,他工作在C科技园区,从家开车到公司上班,有L1,L2两条路线可供选择.L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为,.
图2
(1)若走L1路线,求最多遇到1次红灯的概率;
(2)若走L2路线,求遇到红灯次数X的数学期望;
(3)按照“平均遇到红灯次数最少”的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由.
19.(17分)已知某精密制造企业根据长期检测结果,得到生产的产品的质量差服从正态分布N(μ,σ2),并把质量差在(μ-σ,μ+σ)内的产品称为优等品,质量差在(μ+σ,μ+2σ)内的产品称为一等品,优等品与一等品统称为正品,其余范围内的产品作为废品处理.现从该企业生产的正品中随机抽取1 000件,测得产品质量差的样本数据统计如图3.
(1)根据大量的产品检测数据,检查样本数据的方差的近似值为100,用样本平均数作为μ的近似值,用样本标准差s作为σ的估计值,记质量差X~N(μ,σ2),求该企业生产的产品为正品的概率P(同一组中的数据用该组区间的中点值代表);
(2)假如企业包装时要求把2件优等品和n(n≥2,且n∈N*)件一等品装在同一个箱子中,质检员从某箱子中摸出2件产品进行检验,若抽取到的2件产品等级相同,则该箱产品记为A,否则该箱产品记为B.
①试用含n的代数式表示某箱产品抽检被记为B的概率p;
②设抽检5箱产品恰有3箱被记为B的概率为f(p),求当n为何值时,f(p)取得最大值,并求出最大值.
图3
第8章 概率 单元测试卷 参考答案
1.D 因为m=1-0.5-0.2=0.3,所以E(ξ)=1×0.5+3×0.3+5×0.2=2.4.
2.D 因为随机变量ξ服从正态分布N(1,4),所以μ=1,σ=2,由正态分布的对称性可得,P(ξ<3)=0.5+P(1-2<ξ<1+2)≈0.5+×0.683=0.841 5.故选D.
3.D 随机变量X服从超几何分布,其中N=10,M=6,n=3,则P(X=2)==.
4.B 依题意可得X的可能值为200,180,160,
P(X=200)=0.4,P(X=180)=0.3,P(X=160) =0.3,
则E(X)=200×0.4+(180+160)×0.3=182.
5.C 根据随机变量X的分布列可得到E(X)=-1×+0×A+1×B=-+B=,∴B=,
∵+A+B=1,∴A=,D(X)=(-1-)2×+(0-)2×+(1-)2×=,
则D(3X-2)=9×D(X)=9×=5.
6.A ∵P(X≥1)=0.657,∴1-(1-p)3=0.657,即(1-p)3=0.343,解得p=0.3.
∴P(04)===0.2,故选A.
7.A 令A1=“玩手机时间超过2 h的学生”,
A2=“玩手机时间不超过2 h的学生”,
B=“任意调查一人,此人近视”,则Ω=A1∪A2,且A1,A2互斥,
P(A1)=0.4,P(A2)=0.6,P(B|A1)=0.6,P(B)=0.3,
依题意,P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)=0.4×0.6+0.6×P(B|A2)=0.3,
解得P(B|A2)=,所以所求近视的概率为.
8.C 根据题意,学生发球次数为1,即一次发球成功的概率P(X=1)=p;发球次数为2,即第一次发球不成功第二次发球成功的概率P(X=2)=p(1-p);发球次数为3,即前两次发球都不成功的概率P(X=3)=(1-p)2.则E(X)=p+2p(1-p)+3(1-p)2=p2-3p+3.依题意有E(X)>1.75,则p2-3p+3>1.75,解得p>或p<.结合p的实际意义,可得09.BC A中,P(X=2)=()4()2=,所以A错;
B中,因为P(X<4)=0.3,所以=0.3,所以n=10,所以B对;
C中,P(η=1)+P(η=0)=3P(η=0)=1,所以P(η=0)=,所以C对;
D中,因为随机变量x服从正态分布N(2,σ2),所以该正态分布曲线关于直线x=2对称,
又P(X<4)=0.9,所以P(010.BC 由二进制数A的特点知每一个数位上的数字只能填0,1,且每个数位上的数字再填时互不影响,故以后的5位数中后4位的所有结果有4类:
①后4个数出现4个0,X=0,记其概率为P(X=0)=()4=;
②后4个数位只出现1个1,X=1,记其概率为P(X=1)=()1()3=;
③后4位数位出现2个1,X=2,记其概率为P(X=2)=()2·()2=;
④后4个数位上出现3个1,X=3,记其概率为P(X=3)=()3·()1=;
⑤后4个数位都出现1,X=4,记其概率为P(X=4)=()4=.
故X~B(4,),故A错误,B正确.
∵X~B(4,),∴E(X)=4×=,故C正确.
∵X~B(4,),∴X的方差D(X)=4××=,故D错误.
故选BC.
11.CD X的可能取值为2,3,4,5,6,7,8,则X的分布列为
X 2 3 4 5 6 7 8
P
则E(X)=2×+3×+4×+5×+6×+7×+8×=5,
f1(x)=x2+x3+x4+x5+x6+x7+x8,
∴g(x)=f '1(x)=x+x2+x3+x4+x5+x6+x7,
g(1)=++++++=5,
g(2)=×2+×22+×23+×24+×25+×26+×27=,
f1(2)=×22+×23+×24+×25+×26+×27+×28=.故选CD.
12. ∵P(B)==,P(AB)==,
∴P(A|B)==.
13.0.947 7 4个病人服用新药相当于做了4重伯努利试验,设服用新药的4个病人中被治愈的人数为X,则X~B(4,0.9),所求概率为P(X≥3)=P(X=3)+P(X=4)=×0.93×0.11+×0.94×0.10=0.291 6+0.656 1=0.947 7.
14. 30 因为每道题相互不影响,且每道题答对的概率都为,所以该学生在面试时恰好答对2道题的概率是P=()2·()1=.
设该学生在面试时答对题目数为X,则随机变量X~B(3,),则E(X)=3×=2.
设该同学面试的得分为Y,则Y=20X-10(3-X)=30X-30,则E(Y)=E(30X-30)=30E(X)-30=30×2-30=30.
15.(1)从6人中任选3人,选法共有=20(种),
其中男生甲和女生乙都不被选中的概率为=.
故男生甲或女生乙被选中的概率为1-=.
(2)由题知,P(A)==.又P(B)=P(A)=,P(AB)==,所以P(A|B)==.
16.(1)由题意可得10×(0.002+0.004+0.015+0.02+0.034+a)=1,解得a=0.025,
∴这个样本的项目规划合格率为10×(0.02+0.034+0.025)×100%=79%,
这个样本的项目规划优秀率为10×(0.034+0.025)×100%=59%.
(2)由题意可得等级不满意的学生中,硕士研究生有×9=3(人),则X的取值可能为0,1,2,3.
P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==.
∴X的分布列为
X 0 1 2 3
P
∴E(X)=0×+1×+2×+3×=1.
17.(1)由题意得,
P(μ-σ0.683,
P(μ-2σP(μ-3σ所以仅满足其中一个,则该生产设备为丙级.
(2)由题中表知,不合格的包装共有6袋,则从生产线上随机抽一袋,其不合格的概率为=,
由题意知Y~B(5,),
所以E(Y)=5×=0.3.
18.(1)设“走L1路线最多遇到1次红灯”为事件A,则A包括没有遇到红灯和只遇到1次红灯两种情况,则P(A)=×(1-)3+××(1-)2=,则走L1路线最多遇到1次红灯的概率为.
(2)依题意得,X的可能取值为0,1,2.
P(X=0)=(1-)×(1-)=,
P(X=1)=×(1-)+(1-)×=,
P(X=2)=×=.
X的分布列为
X 0 1 2
P
所以E(X)=×0+×1+×2=.
(3)设选择L1路线遇到红灯次数为Y,则Y~B(3,),
所以E(Y)=3×=.因为E(X)19.(1)由题意估计从该企业生产的正品中随机抽取1 000件的平均数为=0.010×10×+0.020×10×+0.045×10×+0.020×10×+0.005×10×=70,∴μ==70,
样本方差s2=100,∴σ≈=10,∴X~N(70,100),
则优等品为质量差在(μ-σ,μ+σ)内,即(60,80),
一等品质量差在(μ+σ,μ+2σ)内,即(80,90),
∴正品为质量差在(60,80)和(80,90)内,即(60,90),
∴P=P(60(2)①从n+2件正品中任选2个,有种选法,其中等级相同的有+种选法,
∴某箱产品抽检被记录为B的概率为
p=1-=1-=.
②由题意,一箱产品抽检被记为B的概率为p,则5箱产品恰有3箱被记录为B的概率为:
f(p)=p3(1-p)2=10p3(1-2p+p2)=10(p3-2p4+p5),
∴f '(p)=10(3p2-8p3+5p4)=10p2(3-8p+5p2)=10p2(p-1)(5p-3),
∴当p∈(0,)时,f '(p)>0,函数f(p)单调递增,
当p∈(,1)时,f '(p)<0,函数f(p)单调递减,
∴当p=时,f(p)取得最大值,
f()=×()3×(1-)2=,
此时,p==,解得n=3.
∴n=3时,f(p)最大,最大值为.
附:若随机变量X服从正态分布N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.683,P(μ-2σ≤X≤μ+2σ)≈0.954,P(μ-3σ≤X≤μ+3σ)≈0.997.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知离散型随机变量ξ的分布列为则均值E(ξ)等于 ( )
ξ 1 3 5
P 0.5 m 0.2
A.1 B.0.6 C.2+3m D.2.4
2.设随机变量ξ服从正态分布N(1,4),则P(ξ<3)的值约为 ( )
A.0.173 7 B.0.347 4 C.0.683 7 D.0.841 5
3.甲、乙两人参加青年志愿者的选拔,选拔以现场答题的方式进行.已知在备选的10道试题中,甲能答对其中的6道题,乙能答对其中的8道题.规定每次考试都从备选题中随机抽出3道题进行测试,设甲答对的试题数为X,则X=2的概率为 ( )
A. B. C. D.
4.小林从A地出发去往B地,1小时内到达的概率为0.4,1小时10分到达的概率为0.3,1小时20分到达的概率为0.3.现规定1小时内到达的奖励为200元,若超过1小时到达,则每超过1分钟奖励少2元.设小林最后获得的奖励为X元,则E(X)= ( )
A.176 B.182 C.184 D.186
5.随机变量X的分布列如表所示,若E(X)=,则D(3X-2)= ( )
X -1 0 1
P A B
A.3 B. C.5 D.9
6.若随机变量X~B(3,p),Y~N(2,σ2),若P(X≥1)=0.657,P(0
A.0.2 B.0.3 C.0.7 D.0.8
7.长时间玩手机可能影响视力,据调查,某校学生大约30%的人近视,而该校大约有40%的学生每天玩手机超过2 h,这些人的近视率约为60%.现从每天玩手机不超过2 h的学生中任意调查一名学生,则他近视的概率为 ( )
A. B. C. D.
8.体育课的排球发球项目考试的规则是:每位学生最多可发球3次,一旦发球成功,则停止发球,否则一直发到3次为止.设学生一次发球成功的概率为p(p≠0),发球次数为X,若X的数学期望E(X)>1.75,则p的取值范围是 ( )
A.(0,) B.(,1) C.(0,) D.(,1)
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列说法正确的是 ( )
A.设随机变量X服从二项分布B(6,),则P(X=2)=
B.设离散型随机变量X等可能取1,2,3,…,n,若P(X<4)=0.3,则n=10
C.设离散型随机变量η服从两点分布,若P(η=1)=2P(η=0),则P(η=0)=
D.设随机变量x服从正态分布N(2,σ2)且P(X<4)=0.9,则P(0
A.X服从两点分布 B.X服从二项分布
C.X的均值E(X)= D.X的方差D(X)=
11.已知随机变量X的取值为不大于n(n∈N*)的非负整数,它的概率分布列为:
X 0 1 2 3 … n
P p0 p1 p2 p3 … pn
其中pi(i=0,1,2,3,…,n)满足pi∈[0,1],且p0+p1+p2+…+pn=1.定义由X生成的函数f(x)=p0+p1x+p2x2+p3x3+…+pixi+…+pnxn,g(x)为函数f(x)的导函数,E(X)为随机变量X的期望.现有一枚质地均匀的正四面体骰子,四个面的点数分别为1,2,3,4,将这枚骰子连续抛掷两次,记向下点数之和为X,此时由X生成的函数为f1(x),则 ( )
A.E(X)=g(2) B.f1(2)= C.E(X)=g(1) D.f1(2)=
三、填空题:本题共3小题,每小题5分,共15分.
12.由1,2组成的有重复数字的三位数中,若用A表示事件“十位数字为1”,用B表示事件“百位数字为1”,则P(A|B)= .
13.一个病人服用某种新药后被治愈的概率为0.9,则服用这种新药的4个病人中至少3人被治愈的概率为_________.(用数字作答)
14.某高校进行招生面试,评分规则是:共设3道题,每道题答对给20分、答错倒扣10分(每道题都必须回答,但相互不影响).设某学生每道题答对的概率都为,则该学生在面试时恰好答对2道题的概率是 ,该学生在面试时得分的期望值为 分.(本题第一空2分,第二空3分)
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)某班包括男生甲和女生乙在内共有6名班干部,其中男生4人,女生2人,从中任选3人参加义务劳动.
(1)求男生甲或女生乙被选中的概率;
(2)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(A)和P(A|B).
16.(15分)为积极吸纳人才创业,繁荣地方经济,某市特别打造了大学生智慧孵化园区项目,为了了解大学生对产业园创业孵化项目的满意度,从有意来本市创业的大学生中随机抽取若干大学生对该项目进行评分(满分100分),绘制成如图1所示的频率分布直方图,
图1
并将分数从低到高分为四个等级:
满意度评分 低于60分 60分到79分 80分到89分 不低于90分
满意度等级 不满意 基本满意 满意 非常满意
(1)若规定:分数不少于70分称为项目规划合格,不少于80分称为项目规划优秀.求出这个样本的项目规划合格率和优秀率.
(2)在等级为不满意的学生中,硕士研究生占,现从该等级大学生中按学历分层抽取9人了解不满意的原因,并从中选取3人担任项目督导员.记X为硕士督导员的人数,求X的分布列及数学期望E(X).
17.(15分)为了评估某大米包装生产设备的性能,从该设备包装的大米中随机抽取100袋作为样本,称其质量为
质量/kg 9.5 9.6 9.7 9.8 9.9 10.0 10.1 10.2 10.3 10.4 10.5 10.6 10.7 10.8 合计
袋数 1 1 3 5 6 19 34 18 3 4 2 1 2 1 100
经计算:样本的平均值μ≈10.10,标准差σ≈0.21.
(1)为评判该生产线的性能,从该生产线中任意抽取一袋,设其质量为X(单位:kg),并根据以下不等式进行评判.
①P(μ-σ
(2)将质量小于或等于μ-2σ与质量大于μ+2σ的产品的包装认为是不合格的包装,从生产线上随机抽取5袋大米,求其中不合格包装袋数Y的均值E(Y).
18.(17分)如图2,李先生家住H小区,他工作在C科技园区,从家开车到公司上班,有L1,L2两条路线可供选择.L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为,.
图2
(1)若走L1路线,求最多遇到1次红灯的概率;
(2)若走L2路线,求遇到红灯次数X的数学期望;
(3)按照“平均遇到红灯次数最少”的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由.
19.(17分)已知某精密制造企业根据长期检测结果,得到生产的产品的质量差服从正态分布N(μ,σ2),并把质量差在(μ-σ,μ+σ)内的产品称为优等品,质量差在(μ+σ,μ+2σ)内的产品称为一等品,优等品与一等品统称为正品,其余范围内的产品作为废品处理.现从该企业生产的正品中随机抽取1 000件,测得产品质量差的样本数据统计如图3.
(1)根据大量的产品检测数据,检查样本数据的方差的近似值为100,用样本平均数作为μ的近似值,用样本标准差s作为σ的估计值,记质量差X~N(μ,σ2),求该企业生产的产品为正品的概率P(同一组中的数据用该组区间的中点值代表);
(2)假如企业包装时要求把2件优等品和n(n≥2,且n∈N*)件一等品装在同一个箱子中,质检员从某箱子中摸出2件产品进行检验,若抽取到的2件产品等级相同,则该箱产品记为A,否则该箱产品记为B.
①试用含n的代数式表示某箱产品抽检被记为B的概率p;
②设抽检5箱产品恰有3箱被记为B的概率为f(p),求当n为何值时,f(p)取得最大值,并求出最大值.
图3
第8章 概率 单元测试卷 参考答案
1.D 因为m=1-0.5-0.2=0.3,所以E(ξ)=1×0.5+3×0.3+5×0.2=2.4.
2.D 因为随机变量ξ服从正态分布N(1,4),所以μ=1,σ=2,由正态分布的对称性可得,P(ξ<3)=0.5+P(1-2<ξ<1+2)≈0.5+×0.683=0.841 5.故选D.
3.D 随机变量X服从超几何分布,其中N=10,M=6,n=3,则P(X=2)==.
4.B 依题意可得X的可能值为200,180,160,
P(X=200)=0.4,P(X=180)=0.3,P(X=160) =0.3,
则E(X)=200×0.4+(180+160)×0.3=182.
5.C 根据随机变量X的分布列可得到E(X)=-1×+0×A+1×B=-+B=,∴B=,
∵+A+B=1,∴A=,D(X)=(-1-)2×+(0-)2×+(1-)2×=,
则D(3X-2)=9×D(X)=9×=5.
6.A ∵P(X≥1)=0.657,∴1-(1-p)3=0.657,即(1-p)3=0.343,解得p=0.3.
∴P(0
7.A 令A1=“玩手机时间超过2 h的学生”,
A2=“玩手机时间不超过2 h的学生”,
B=“任意调查一人,此人近视”,则Ω=A1∪A2,且A1,A2互斥,
P(A1)=0.4,P(A2)=0.6,P(B|A1)=0.6,P(B)=0.3,
依题意,P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)=0.4×0.6+0.6×P(B|A2)=0.3,
解得P(B|A2)=,所以所求近视的概率为.
8.C 根据题意,学生发球次数为1,即一次发球成功的概率P(X=1)=p;发球次数为2,即第一次发球不成功第二次发球成功的概率P(X=2)=p(1-p);发球次数为3,即前两次发球都不成功的概率P(X=3)=(1-p)2.则E(X)=p+2p(1-p)+3(1-p)2=p2-3p+3.依题意有E(X)>1.75,则p2-3p+3>1.75,解得p>或p<.结合p的实际意义,可得0
B中,因为P(X<4)=0.3,所以=0.3,所以n=10,所以B对;
C中,P(η=1)+P(η=0)=3P(η=0)=1,所以P(η=0)=,所以C对;
D中,因为随机变量x服从正态分布N(2,σ2),所以该正态分布曲线关于直线x=2对称,
又P(X<4)=0.9,所以P(0
①后4个数出现4个0,X=0,记其概率为P(X=0)=()4=;
②后4个数位只出现1个1,X=1,记其概率为P(X=1)=()1()3=;
③后4位数位出现2个1,X=2,记其概率为P(X=2)=()2·()2=;
④后4个数位上出现3个1,X=3,记其概率为P(X=3)=()3·()1=;
⑤后4个数位都出现1,X=4,记其概率为P(X=4)=()4=.
故X~B(4,),故A错误,B正确.
∵X~B(4,),∴E(X)=4×=,故C正确.
∵X~B(4,),∴X的方差D(X)=4××=,故D错误.
故选BC.
11.CD X的可能取值为2,3,4,5,6,7,8,则X的分布列为
X 2 3 4 5 6 7 8
P
则E(X)=2×+3×+4×+5×+6×+7×+8×=5,
f1(x)=x2+x3+x4+x5+x6+x7+x8,
∴g(x)=f '1(x)=x+x2+x3+x4+x5+x6+x7,
g(1)=++++++=5,
g(2)=×2+×22+×23+×24+×25+×26+×27=,
f1(2)=×22+×23+×24+×25+×26+×27+×28=.故选CD.
12. ∵P(B)==,P(AB)==,
∴P(A|B)==.
13.0.947 7 4个病人服用新药相当于做了4重伯努利试验,设服用新药的4个病人中被治愈的人数为X,则X~B(4,0.9),所求概率为P(X≥3)=P(X=3)+P(X=4)=×0.93×0.11+×0.94×0.10=0.291 6+0.656 1=0.947 7.
14. 30 因为每道题相互不影响,且每道题答对的概率都为,所以该学生在面试时恰好答对2道题的概率是P=()2·()1=.
设该学生在面试时答对题目数为X,则随机变量X~B(3,),则E(X)=3×=2.
设该同学面试的得分为Y,则Y=20X-10(3-X)=30X-30,则E(Y)=E(30X-30)=30E(X)-30=30×2-30=30.
15.(1)从6人中任选3人,选法共有=20(种),
其中男生甲和女生乙都不被选中的概率为=.
故男生甲或女生乙被选中的概率为1-=.
(2)由题知,P(A)==.又P(B)=P(A)=,P(AB)==,所以P(A|B)==.
16.(1)由题意可得10×(0.002+0.004+0.015+0.02+0.034+a)=1,解得a=0.025,
∴这个样本的项目规划合格率为10×(0.02+0.034+0.025)×100%=79%,
这个样本的项目规划优秀率为10×(0.034+0.025)×100%=59%.
(2)由题意可得等级不满意的学生中,硕士研究生有×9=3(人),则X的取值可能为0,1,2,3.
P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==.
∴X的分布列为
X 0 1 2 3
P
∴E(X)=0×+1×+2×+3×=1.
17.(1)由题意得,
P(μ-σ
P(μ-2σ
(2)由题中表知,不合格的包装共有6袋,则从生产线上随机抽一袋,其不合格的概率为=,
由题意知Y~B(5,),
所以E(Y)=5×=0.3.
18.(1)设“走L1路线最多遇到1次红灯”为事件A,则A包括没有遇到红灯和只遇到1次红灯两种情况,则P(A)=×(1-)3+××(1-)2=,则走L1路线最多遇到1次红灯的概率为.
(2)依题意得,X的可能取值为0,1,2.
P(X=0)=(1-)×(1-)=,
P(X=1)=×(1-)+(1-)×=,
P(X=2)=×=.
X的分布列为
X 0 1 2
P
所以E(X)=×0+×1+×2=.
(3)设选择L1路线遇到红灯次数为Y,则Y~B(3,),
所以E(Y)=3×=.因为E(X)
样本方差s2=100,∴σ≈=10,∴X~N(70,100),
则优等品为质量差在(μ-σ,μ+σ)内,即(60,80),
一等品质量差在(μ+σ,μ+2σ)内,即(80,90),
∴正品为质量差在(60,80)和(80,90)内,即(60,90),
∴P=P(60
∴某箱产品抽检被记录为B的概率为
p=1-=1-=.
②由题意,一箱产品抽检被记为B的概率为p,则5箱产品恰有3箱被记录为B的概率为:
f(p)=p3(1-p)2=10p3(1-2p+p2)=10(p3-2p4+p5),
∴f '(p)=10(3p2-8p3+5p4)=10p2(3-8p+5p2)=10p2(p-1)(5p-3),
∴当p∈(0,)时,f '(p)>0,函数f(p)单调递增,
当p∈(,1)时,f '(p)<0,函数f(p)单调递减,
∴当p=时,f(p)取得最大值,
f()=×()3×(1-)2=,
此时,p==,解得n=3.
∴n=3时,f(p)最大,最大值为.
