选择性必修第一册人教B版-第一章-单元测试卷(含解析)
文档属性
| 名称 | 选择性必修第一册人教B版-第一章-单元测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 335.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-07 00:00:00 | ||
图片预览




文档简介
第一章 空间向量与立体几何
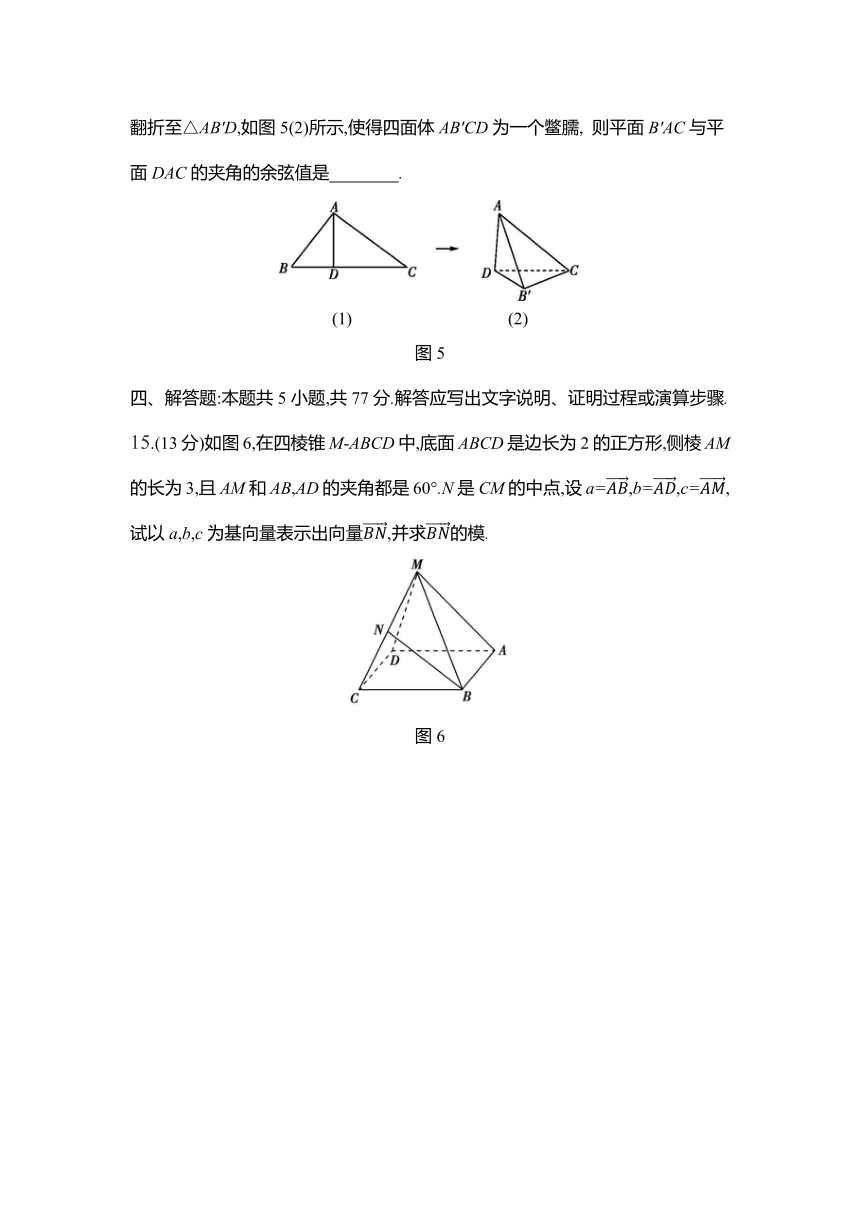
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知a=(-3,2,5),b=(1,5,-1),则a·(a+3b)= ( )
A.(0,34,10) B.(-3,19,7) C.44 D.23
2.空间中,与向量a=(3,0,4)同向共线的单位向量e= ( )
A.(1,0,1) B.(1,0,1)或(-1,0,-1)
C.(,0,) D.(,0,)或(-,0,-)
3.已知正方体ABCD-A1B1C1D1中,点E为上底面A1B1C1D1的中心,若=+x+y,则x,y的值分别为 ( )
A.1,1 B.1, C., D.,
4.直三棱柱ABC-A1B1C1中,若∠BAC=90°,AB=AC=AA1,则异面直线BA1与AC1所成角为 ( )
A.30° B.45° C.60° D.90°
5.已知空间三点O(0,0,0), A(-1,1,0), B(0,1,1), 在直线OA上有一点H满足BH⊥OA,则点H的坐标为 ( )
A.(-2, 2, 0) B.(2, -2, 0) C.(-,,0) D.(,-,0)
6.在正四棱柱ABCD-A'B'C'D'中,底面边长为2,侧棱长为4,E,F分别是棱AB,BC的中点,则点D'到平面B'EF的距离为 ( )
A. B. C. D.
7.如图1,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,PA=AB,则直线PC与平面PBD所成角的正弦值为 ( )
A. B. C. D.
图1
8.在正方体ABCD-A1B1C1D1中,O是BD的中点,点P在线段B1D1上,直线OP与平面A1BD所成的角为α,则sin α的取值范围是 ( )
A.[,] B.[,] C.[,] D.[,]
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列命题为真命题的是 ( )
A.直线l的方向向量a=(1,-1,2),直线m的方向向量b=(2,1,-),则l与m垂直
B.直线l的方向向量a=(0,1,-1),平面α的一个法向量为n=(1,-1,-1),则l⊥α
C.平面α,β的一个法向量分别为n1=(0,1,3),n2=(1,0,2),则α∥β
D.平面α经过三点A(1,0,-1),B(0,1,0),C(-1,2,0),向量n=(1,u,t)是平面α的一个法向量,则u+t=1
10.如图2,正三棱柱ABC-A1B1C1的侧面是边长为2的正方形,D,E分别是BB1,AC的中点,则下列结论成立的是 ( )
图2
A.直线A1D与直线BC是异面直线
B.直线BE与平面A1CD不平行
C.直线AC与直线A1D所成角的余弦值等于
D.直线CD与平面AA1C1C所成角的正弦值等于
11.如图3,在正方形ABCD中,点E,F分别是线段AD,BC上的动点,且AE=BF,AC与EF交于G,EF在AB与CD之间从AB向CD滑动,但与AB和CD均不重合.在EF任一确定位置,将四边形EFCD沿直线EF折起,使平面EFCD⊥平面ABFE,如图4所示,则下列选项中正确的是 ( )
图3 图4
A.∠AGC的角度不会发生变化
B.二面角G-AC-B先变大后变小
C.AC与平面ABFG所成的角变小
D.AC与EF所成的角先变小后变大
三、填空题:本题共3小题,每小题5分,共15分.
12.已知边长为4的正方形ABCD所在平面外一点P与正方形的中心O的连线PO垂直于平面ABCD,且PO=6,则PO的中点M到△PBC的重心N的距离为 .
13.已知A(0,0,-x),B(1,,2),C(x,,2)三点,点M在平面ABC内,O是平面ABC外一点,且=x+2x+4,则x= ,与的夹角为______.(本题第一空2分,第二空3分)
14.在中国古代数学著作《九章算术》中,鳖臑是指四个面都是直角三角形的四面体.如图5(1),在Rt△ABC中,AD为斜边BC上的高,AB=3,AC=4,现将△ABD沿AD翻折至△AB'D,如图5(2)所示,使得四面体AB'CD为一个鳖臑, 则平面B'AC与平面DAC的夹角的余弦值是 .
(1) (2)
图5
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)如图6,在四棱锥M-ABCD中,底面ABCD是边长为2的正方形,侧棱AM的长为3,且AM和AB,AD的夹角都是60°.N是CM的中点,设a=,b=,c=,试以a,b,c为基向量表示出向量,并求的模.
图6
16.(15分)如图7,在四棱锥P-ABCD中,PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=,PA=AD=2,AB=BC=1.
(1)求平面PAB与平面PCD夹角的余弦值.
(2)定义:两条异面直线之间的距离是其中一条直线上任意一点到另一条直线距离的最小值.利用此定义求异面直线PB与CD之间的距离.
图7
17.(15分)如图8,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,侧面PAD⊥底面ABCD,∠BCD=60°,PA=PD=,E是BC的中点,点Q在侧棱PC上.
(1)求证:AD⊥PB;
(2)若=λ,当PA∥平面DEQ时,求λ的值.
图8
18.(17分)中国是风筝的故乡,南方称“鹞”,北方称“鸢”.如图9,某种风筝的骨架模型是四棱锥P-ABCD,其中AC⊥BD于点O,OA=OB=OD=4,OC=8,PO⊥平面ABCD.
图9
(1)求证:PD⊥AC;
(2)试验表明,当PO=OA时,风筝表现最好,求此时直线PD与平面PBC所成角的正弦值.
19.(17分)条件①:图10(1)中tan 2B=-.
条件②:图 10(1)中=+.
条件③:图10(2)中三棱锥A-BCD的体积为.
从以上三个条件中任选一个,补充在问题(2)中的横线上,并加以解答.
图10
如图10(1)所示,在△ABC中,∠ACB=45°,BC=3,过点A作AD⊥BC,垂足D在线段BC上,沿AD将△ABD折起,使∠BDC=90°(如图10(2)),点E,M分别为棱BC,AC的中点.
(1)求证:CD⊥ME;
(2)已知 ,试在棱CD上确定一点N,使得EN⊥BM,并求二面角M-BN-C的余弦值.
注:如果选择多个条件分别解答,按第一个解答计分.
第一章 空间向量与立体几何
1.C a+3b=(-3,2,5)+3(1,5,-1)=(0,17,2),则a·(a+3b)=(-3,2,5)·(0,17,2)=0+34+10=44.
2.C ∵|a|==5,∴与a同向共线的单位向量e==(,0,).
3.C 连接A1E,=+=+(+)=++,故x=y=.
4.C 方法一 建立如图D 1所示的空间直角坐标系,设AB=1,则A(0,0,0),B(1,0,0),A1(0,0,1),C1(0,1,1),∴=(-1,0,1),=(0,1,1),
∴cos<,>===.
∴<,>=60°,即异面直线BA1与AC1所成角为60°.
图D 1
方法二 ∵∠BAC=90°,AB=AC=AA1,
∴可将直三棱柱ABC-A1B1C1补形成为正方体,
再将BA1平移至A1与C1重合,连接此时的AB,则此时的△ABC1为正三角形,
∴此时∠AC1B为异面直线BA1与AC1所成的角,则所求角为60°.
5.C 由=(-1,1,0),且点H在直线OA上,可设H(-λ,λ,0),则=(-λ,λ-1,-1).
又BH⊥OA,∴·=0,即(-λ,λ-1,-1)·(-1,1,0)=0,即λ+λ-1=0,解得λ=,∴H(-,,0).
6.D 建立如图D 2所示的空间直角坐标系,
图D 2
则E(2,,0),F(,2,0),B'(2,2,4),D'(0,0,4),所以=(-,,0),=(0,,4).
设平面B'EF的一个法向量为n=(x,y,z),则即
令y=1,得n=(1,1,-).
连接B'D',则=(-2,-2,0),所以点D'到平面B'EF的距离为||=.
7.C 如图D 3,以A为坐标原点,分别以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系.
图D 3
设AB=1,则B(1,0,0),D(0,1,0),P(0,0,1),C(1,1,0),
所以=(1,0,-1),=(0,1,-1),=(1,1,-1).
设平面PBD的法向量为n=(x,y,z),
由令x=1,则y=z=1,
所以n=(1,1,1).
设直线PC与平面PBD所成的角为θ,
sin θ=|cos<,n>|===,
所以直线PC与平面PBD所成角的正弦值为.
8.A 设正方体的棱长为1,=λ(0≤λ≤1),以B1为坐标原点,分别以B1A1,B1C1,B1B所在直线为x轴、y轴、z轴建立空间直角坐标系,如图D 4所示,
图D 4
则O(,,1),P(λ,λ,0),∴=(λ-,λ-,-1).
连接AB1,AC1,∵B1C1⊥平面AB1,∴B1C1⊥A1B,又A1B⊥AB1,AB1∩B1C1=B1,∴A1B⊥平面AB1C1,
∴AC1⊥A1B,
同理可得AC1⊥A1D,又A1D∩A1B=A1,则AC1⊥平面A1BD.
又A(1,0,1),C1(0,1,0),
∴=(-1,1,-1)是平面A1BD的一个法向量,
∴sin α=|cos<,>|=.
故当λ=时,sin α取得最大值,当λ=0或λ=1时,sin α取得最小值,即sin α的取值范围是[,].
9.AD 对于A,∵a=(1,-1,2),b=(2,1,-),∴a·b=1×2+(-1)×1+2×(-)=0,∴a⊥b,
∴直线l与m垂直,A正确.
对B,∵a=(0,1,-1),n=(1,-1,-1),∴a·n=0×1+1×(-1)+(-1)×(-1)=0,∴a⊥n,∴l∥α或l α,B错误.
对于C,∵n1=(0,1,3),n2=(1,0,2),∴n1与n2不共线,∴α∥β不成立,C错误.
对于D,∵A(1,0,-1),B(0,1,0),C(-1,2,0),∴=(-1,1,1),=(-1,1,0),又向量n =(1,u,t)是平面α的一个法向量,∴
即则u+t=1,D正确.
10.AC 对于A,∵BC 平面BCC1B1,A1D∩平面BCC1B1=D,D BC,∴直线A1D与直线BC是异面直线,故A正确.
对于B,由题意知正三棱柱ABC-A1B1C1的所有棱长都为2,
则△ABC是边长为2的正三角形,且AE=EC,
∴BE⊥AC,且BE=.
∵平面ABC⊥平面ACC1A1,平面ABC∩平面ACC1A1=AC,
∴BE⊥平面ACC1A1.
取A1C1中点F,连接EF,则在正方形ACC1A1中,EF⊥AC.以E为坐标原点,直线EA,EF,EB分别为x轴、y轴、z轴,建立空间直角坐标系,如图D 5,
图D 5
则E(0,0,0),B(0,0,),C(-1,0,0),A(1,0,0),A1(1,2,0),D(0,1,),
则=(0,0,),=(-2,-2,0),=(1,1,).∴=+,
根据共面向量定理,可知与,共面.
∵∩=C,EB 平面A1CD,∴BE∥平面A1CD,故B错误.
对于C,=(-2,0,0),=(-1,-1,),
∴直线AC与直线A1D所成角的余弦值为
|cos<,>|=||==,故C正确.
对于D,由题意得,=(1,1,),平面AA1C1C的一个法向量为m=(0,0,1).
设直线CD与平面AA1C1C所成角为θ,
则直线CD与平面AA1C1C所成角的正弦值为
sin θ=||==,故D错误.
故选AC.
11.ACD 以E为坐标原点,EA,EF,ED所在直线分别为x轴、y轴、z轴建立如图D 6所示的空间直角坐标系,
图D 6
设正方形的边长为1,AE=a(0对于A选项,=(-a,a,0),=(0,a-1,a-1),
∴cos∠AGC===-,即∠AGC=120°,
∴∠AGC的角度不会发生变化,故选项A正确.
对于B选项,=(-a,a,0),=(-a,1,1-a),=(0,1,0),=(a,0,a-1),设平面AGC的一个法向量为n=(x1,y1,z1),则
则可取n=(1,1,-1),
设平面ACB的一个法向量为p=(x2,y2,z2),则
则可取p=(1-a,0,a),
设二面角G-AC-B的大小为β,则由图D 1-6并结合n与p的方向可得,
cos β=cos===,
当0而y=2a2-2a+1的对称轴为直线a=,
∴当a∈(0,]时,cos β随着a的增大而减小,
又cos β>0,β在此时为锐角.
故二面角G-AC-B随着a的增大而增大.
同理,当故二面角G-AC-B一直增大,选项B错误.
对于C选项,易知平面ABFG的一个法向量为m=(0,0,1),设AC与平面ABFG所成的角为α,
显然与m的夹角为锐角,则sin α=cos<,m>=====,
∵a∈(0,1),∴y=a+单调递减,则sin α随着a的增大而减小,∴AC与平面ABFG所成角变小,故选项C正确.
对于D选项,设与所成的角为θ,=(-a,1,1-a),=(0,1,0),
∴cos θ===,显然θ为锐角,
而y=2a2-2a+2的对称轴为直线a=,且a∈(0,1),
∴随着a的增大y=2a2-2a+2先减小后增大,则随着a的增大cos θ先增大后减小,即AC与EF所成的角先变小后变大,故选项D正确.
12. 依题意建立如图D 7所示的空间直角坐标系,则B (2,2,0),C (-2,2,0),P (0,0,6).
图D 7
由题意得M (0,0,3),N (0,,2),则=(0,,-1).
于是||==.
故M到△PBC的重心N的距离为.
13.-1 由A,B,C,M四点共面可知x+2x+4=1,∴x=-1.∴A(0,0,1),C(-1,,2),∴=(1,,1),=(-1,,1),∴cos<,>==,即与的夹角为.
14. 在Rt△ABC中,由题意知,BC=5,AD=,BD=,CD=,即在四面体AB'C D中,AD=,=,CD=,=3,AC=4,在△中,由三角形的三边关系可知,<<5,
在△中,若∠=90°,则==5,矛盾,
故∠=90°,此时==,
在△中,2+2=DC2,所以∠=90°.
此时∠AD,∠ADC,∠DC,∠AC为直角,满足四面体ACD为一个鳖臑.
如图D 8,在长、宽、高分别为,,的长方体中作出四面体ADC,以D为坐标原点建立空间直角坐标系,
图D 8
则D(0,0,0),A(0,0,),C(,,0),(,0,0),=(0,0,),=(,,0),=(,0,-),
=(0,-,0).
设向量m=(x1,y1,z1)为平面DAC的法向量,向量n=(x2,y2,z2)为平面AC的法向量,
则取x1=,可得平面DAC的一个法向量为m=(,-,0),同理可得平面AC的一个法向量为n=(1,0,),
所以cos===.
所以平面AC与平面DAC夹角的余弦值是.
15.连接AC,∵=+=+=+(-)=+[-(+)]=-++,
∴=-a+b+c.
∵||2=(-a+b+c)2=(|a|2+|b|2+|c|2-2a·b-2a·c+2b·c)=×(22+22+32-0-2×
2×3×cos 60°+2×2×3×cos 60°)=,∴||=.
16.由题意知,PA,AB,AD两两垂直,以{,,}为正交基底建立如图D 9所示的空间直角坐标系Axyz,
图D 9
则A(0,0,0),B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,2).
(1)易知是平面PAB的一个法向量,=(0,2,0).
易得=(1,1,-2),=(0,2,-2).
设平面PCD的一个法向量为m=(x,y,z),
则即令y=1,得z=1,x=1,所以m=(1,1,1)是平面PCD的一个法向量.
因为cos<,m>==,
所以平面PAB与平面PCD夹角的余弦值为.
(2)=(-1,0,2),设Q为直线PB上一点,且=λ=(-λ,0,2λ).连接QC,易得=(-1,1,0),=(0,-1,0),则=+=(-λ,-1,2λ),
则点Q到直线CD的距离d==,因为λ2+λ+=(λ+)2+≥,所以d≥,所以异面直线PB与CD之间的距离为.
17.取AD的中点O,连接PO,BO,∵PA=PD,∴PO⊥AD.∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴PO⊥平面ABCD.∵四边形ABCD为菱形,∠BCD=60°,∴OB⊥AD.以O为坐标原点,建立如图D 10所示的空间直角坐标系Oxyz,
图D 10
则A(1,0,0),B(0,,0),D(-1,0,0),E(-1,,0),P(0,0,1),C(-2,,0).
(1)=(-2,0,0),=(0,,-1),
∴·=(-2,0,0)·(0,,-1)=0,
∴⊥,∴AD⊥PB.
(2)设Q(x,y,z),则=(x,y,z-1).
∵=λ,∴=λ.
∵=(-2,,-1),∴
在平面DEQ中,=(0,,0),=(x+1,y,z)=(1-2λ,λ,1-λ).
设平面DEQ的一个法向量为n=(x1,y1,z1),
由得
令x1=1-λ,可得n=(1-λ,0,2λ-1)是平面DEQ的一个法向量.又PA∥平面DEQ,=(1,0,-1),∴·n=0,即1-λ-(2λ-1)=0,解得λ=.∴当λ=时,PA∥平面DEQ.
18.(1)∵PO⊥平面ABCD,AC 平面ABCD,
∴PO⊥AC,又AC⊥BD,PO∩BD=O,∴AC⊥平面POD,又PD 平面POD,∴PD⊥AC.
(2)如图D 11,以O为坐标原点,分别以,,为x,y,z轴正方向,建立空间直角坐标系Oxyz,
图D 11
则B(4,0,0),C(0,8,0),D(-4,0,0),P(0,0,2),∴=(4,0,-2),=(0,8,-2),=(-4,0,-2).
设m=(a,b,c)为平面PBC的法向量,则即
令c=4,则平面PBC的一个法向量为m=(2,1,4),设直线PD与平面PBC所成角为θ,则sin θ=|cos<,m>|=||==.
19.(1)如题图(2),∵CD⊥AD,CD⊥BD,AD∩BD=D,AD,BD 平面ABD,∴CD⊥平面ABD.
∵AB 平面ABD,∴CD⊥AB.
又M,E分别为AC,BC的中点,∴ME∥AB,∴CD⊥ME.
(2)方案一 选①,在题图(1)所示的△ABC中,由tan 2B=-=,解得tan B=2或tan B=-(舍去).
设AD=CD=x,在Rt△ABD中,tan B===2,
解得x=2,∴BD=1.
以点D为坐标原点,直线DB,DC,DA分别为x轴、y轴、z轴建立如图D 12 所示的空间直角坐标系,
图D 12
则B(1,0,0),C(0,2,0),A(0,0,2),M(0,1,1),E(,1,0),则=(-1,1,1).
设N(0,a,0),0≤a≤2,则=(-,a-1,0).
∵EN⊥BM,∴·=0,
即(-,a-1,0)·(-1,1,1)=0,∴a=,∴N(0,,0),
∴当DN=(即N是CD上靠近点D的一个四等分点)时,EN⊥BM.
设平面BNM的一个法向量为n=(x,y,z),=(-1,,0),
由得令x=1,则n=(1,2,-1).
取平面BNC的一个法向量m=(0,0,1),则cos===-,
又二面角M-BN-C的平面角为锐角,
∴二面角M-BN-C的余弦值为.
方案二 选②,在题图(1)所示的△ABC中,设=λ,则=+=+λ(-)=(1-λ)+λ,又=+,故λ=,即BD=1.
下同选条件①.
方案三 选③,在题图(1)所示的△ABC中,设BD=x(0∵AD⊥CD,∠ACD=45°,∴△ADC为等腰直角三角形,∴AD=CD=3-x.在题图(2)中,AD⊥DC,AD⊥BD,且BD∩DC=D,BD,DC 平面BCD,∴AD⊥平面BCD,
又∠BDC=90°,∴S△BCD=x(3-x),
∴VA-BCD=AD·S△BCD=(3-x)·x(3-x)=,化简得(x-1)2(x-4)=0,解得x=1或x=4(舍去),故BD=1.
下同选条件①.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知a=(-3,2,5),b=(1,5,-1),则a·(a+3b)= ( )
A.(0,34,10) B.(-3,19,7) C.44 D.23
2.空间中,与向量a=(3,0,4)同向共线的单位向量e= ( )
A.(1,0,1) B.(1,0,1)或(-1,0,-1)
C.(,0,) D.(,0,)或(-,0,-)
3.已知正方体ABCD-A1B1C1D1中,点E为上底面A1B1C1D1的中心,若=+x+y,则x,y的值分别为 ( )
A.1,1 B.1, C., D.,
4.直三棱柱ABC-A1B1C1中,若∠BAC=90°,AB=AC=AA1,则异面直线BA1与AC1所成角为 ( )
A.30° B.45° C.60° D.90°
5.已知空间三点O(0,0,0), A(-1,1,0), B(0,1,1), 在直线OA上有一点H满足BH⊥OA,则点H的坐标为 ( )
A.(-2, 2, 0) B.(2, -2, 0) C.(-,,0) D.(,-,0)
6.在正四棱柱ABCD-A'B'C'D'中,底面边长为2,侧棱长为4,E,F分别是棱AB,BC的中点,则点D'到平面B'EF的距离为 ( )
A. B. C. D.
7.如图1,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,PA=AB,则直线PC与平面PBD所成角的正弦值为 ( )
A. B. C. D.
图1
8.在正方体ABCD-A1B1C1D1中,O是BD的中点,点P在线段B1D1上,直线OP与平面A1BD所成的角为α,则sin α的取值范围是 ( )
A.[,] B.[,] C.[,] D.[,]
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列命题为真命题的是 ( )
A.直线l的方向向量a=(1,-1,2),直线m的方向向量b=(2,1,-),则l与m垂直
B.直线l的方向向量a=(0,1,-1),平面α的一个法向量为n=(1,-1,-1),则l⊥α
C.平面α,β的一个法向量分别为n1=(0,1,3),n2=(1,0,2),则α∥β
D.平面α经过三点A(1,0,-1),B(0,1,0),C(-1,2,0),向量n=(1,u,t)是平面α的一个法向量,则u+t=1
10.如图2,正三棱柱ABC-A1B1C1的侧面是边长为2的正方形,D,E分别是BB1,AC的中点,则下列结论成立的是 ( )
图2
A.直线A1D与直线BC是异面直线
B.直线BE与平面A1CD不平行
C.直线AC与直线A1D所成角的余弦值等于
D.直线CD与平面AA1C1C所成角的正弦值等于
11.如图3,在正方形ABCD中,点E,F分别是线段AD,BC上的动点,且AE=BF,AC与EF交于G,EF在AB与CD之间从AB向CD滑动,但与AB和CD均不重合.在EF任一确定位置,将四边形EFCD沿直线EF折起,使平面EFCD⊥平面ABFE,如图4所示,则下列选项中正确的是 ( )
图3 图4
A.∠AGC的角度不会发生变化
B.二面角G-AC-B先变大后变小
C.AC与平面ABFG所成的角变小
D.AC与EF所成的角先变小后变大
三、填空题:本题共3小题,每小题5分,共15分.
12.已知边长为4的正方形ABCD所在平面外一点P与正方形的中心O的连线PO垂直于平面ABCD,且PO=6,则PO的中点M到△PBC的重心N的距离为 .
13.已知A(0,0,-x),B(1,,2),C(x,,2)三点,点M在平面ABC内,O是平面ABC外一点,且=x+2x+4,则x= ,与的夹角为______.(本题第一空2分,第二空3分)
14.在中国古代数学著作《九章算术》中,鳖臑是指四个面都是直角三角形的四面体.如图5(1),在Rt△ABC中,AD为斜边BC上的高,AB=3,AC=4,现将△ABD沿AD翻折至△AB'D,如图5(2)所示,使得四面体AB'CD为一个鳖臑, 则平面B'AC与平面DAC的夹角的余弦值是 .
(1) (2)
图5
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)如图6,在四棱锥M-ABCD中,底面ABCD是边长为2的正方形,侧棱AM的长为3,且AM和AB,AD的夹角都是60°.N是CM的中点,设a=,b=,c=,试以a,b,c为基向量表示出向量,并求的模.
图6
16.(15分)如图7,在四棱锥P-ABCD中,PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=,PA=AD=2,AB=BC=1.
(1)求平面PAB与平面PCD夹角的余弦值.
(2)定义:两条异面直线之间的距离是其中一条直线上任意一点到另一条直线距离的最小值.利用此定义求异面直线PB与CD之间的距离.
图7
17.(15分)如图8,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,侧面PAD⊥底面ABCD,∠BCD=60°,PA=PD=,E是BC的中点,点Q在侧棱PC上.
(1)求证:AD⊥PB;
(2)若=λ,当PA∥平面DEQ时,求λ的值.
图8
18.(17分)中国是风筝的故乡,南方称“鹞”,北方称“鸢”.如图9,某种风筝的骨架模型是四棱锥P-ABCD,其中AC⊥BD于点O,OA=OB=OD=4,OC=8,PO⊥平面ABCD.
图9
(1)求证:PD⊥AC;
(2)试验表明,当PO=OA时,风筝表现最好,求此时直线PD与平面PBC所成角的正弦值.
19.(17分)条件①:图10(1)中tan 2B=-.
条件②:图 10(1)中=+.
条件③:图10(2)中三棱锥A-BCD的体积为.
从以上三个条件中任选一个,补充在问题(2)中的横线上,并加以解答.
图10
如图10(1)所示,在△ABC中,∠ACB=45°,BC=3,过点A作AD⊥BC,垂足D在线段BC上,沿AD将△ABD折起,使∠BDC=90°(如图10(2)),点E,M分别为棱BC,AC的中点.
(1)求证:CD⊥ME;
(2)已知 ,试在棱CD上确定一点N,使得EN⊥BM,并求二面角M-BN-C的余弦值.
注:如果选择多个条件分别解答,按第一个解答计分.
第一章 空间向量与立体几何
1.C a+3b=(-3,2,5)+3(1,5,-1)=(0,17,2),则a·(a+3b)=(-3,2,5)·(0,17,2)=0+34+10=44.
2.C ∵|a|==5,∴与a同向共线的单位向量e==(,0,).
3.C 连接A1E,=+=+(+)=++,故x=y=.
4.C 方法一 建立如图D 1所示的空间直角坐标系,设AB=1,则A(0,0,0),B(1,0,0),A1(0,0,1),C1(0,1,1),∴=(-1,0,1),=(0,1,1),
∴cos<,>===.
∴<,>=60°,即异面直线BA1与AC1所成角为60°.
图D 1
方法二 ∵∠BAC=90°,AB=AC=AA1,
∴可将直三棱柱ABC-A1B1C1补形成为正方体,
再将BA1平移至A1与C1重合,连接此时的AB,则此时的△ABC1为正三角形,
∴此时∠AC1B为异面直线BA1与AC1所成的角,则所求角为60°.
5.C 由=(-1,1,0),且点H在直线OA上,可设H(-λ,λ,0),则=(-λ,λ-1,-1).
又BH⊥OA,∴·=0,即(-λ,λ-1,-1)·(-1,1,0)=0,即λ+λ-1=0,解得λ=,∴H(-,,0).
6.D 建立如图D 2所示的空间直角坐标系,
图D 2
则E(2,,0),F(,2,0),B'(2,2,4),D'(0,0,4),所以=(-,,0),=(0,,4).
设平面B'EF的一个法向量为n=(x,y,z),则即
令y=1,得n=(1,1,-).
连接B'D',则=(-2,-2,0),所以点D'到平面B'EF的距离为||=.
7.C 如图D 3,以A为坐标原点,分别以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系.
图D 3
设AB=1,则B(1,0,0),D(0,1,0),P(0,0,1),C(1,1,0),
所以=(1,0,-1),=(0,1,-1),=(1,1,-1).
设平面PBD的法向量为n=(x,y,z),
由令x=1,则y=z=1,
所以n=(1,1,1).
设直线PC与平面PBD所成的角为θ,
sin θ=|cos<,n>|===,
所以直线PC与平面PBD所成角的正弦值为.
8.A 设正方体的棱长为1,=λ(0≤λ≤1),以B1为坐标原点,分别以B1A1,B1C1,B1B所在直线为x轴、y轴、z轴建立空间直角坐标系,如图D 4所示,
图D 4
则O(,,1),P(λ,λ,0),∴=(λ-,λ-,-1).
连接AB1,AC1,∵B1C1⊥平面AB1,∴B1C1⊥A1B,又A1B⊥AB1,AB1∩B1C1=B1,∴A1B⊥平面AB1C1,
∴AC1⊥A1B,
同理可得AC1⊥A1D,又A1D∩A1B=A1,则AC1⊥平面A1BD.
又A(1,0,1),C1(0,1,0),
∴=(-1,1,-1)是平面A1BD的一个法向量,
∴sin α=|cos<,>|=.
故当λ=时,sin α取得最大值,当λ=0或λ=1时,sin α取得最小值,即sin α的取值范围是[,].
9.AD 对于A,∵a=(1,-1,2),b=(2,1,-),∴a·b=1×2+(-1)×1+2×(-)=0,∴a⊥b,
∴直线l与m垂直,A正确.
对B,∵a=(0,1,-1),n=(1,-1,-1),∴a·n=0×1+1×(-1)+(-1)×(-1)=0,∴a⊥n,∴l∥α或l α,B错误.
对于C,∵n1=(0,1,3),n2=(1,0,2),∴n1与n2不共线,∴α∥β不成立,C错误.
对于D,∵A(1,0,-1),B(0,1,0),C(-1,2,0),∴=(-1,1,1),=(-1,1,0),又向量n =(1,u,t)是平面α的一个法向量,∴
即则u+t=1,D正确.
10.AC 对于A,∵BC 平面BCC1B1,A1D∩平面BCC1B1=D,D BC,∴直线A1D与直线BC是异面直线,故A正确.
对于B,由题意知正三棱柱ABC-A1B1C1的所有棱长都为2,
则△ABC是边长为2的正三角形,且AE=EC,
∴BE⊥AC,且BE=.
∵平面ABC⊥平面ACC1A1,平面ABC∩平面ACC1A1=AC,
∴BE⊥平面ACC1A1.
取A1C1中点F,连接EF,则在正方形ACC1A1中,EF⊥AC.以E为坐标原点,直线EA,EF,EB分别为x轴、y轴、z轴,建立空间直角坐标系,如图D 5,
图D 5
则E(0,0,0),B(0,0,),C(-1,0,0),A(1,0,0),A1(1,2,0),D(0,1,),
则=(0,0,),=(-2,-2,0),=(1,1,).∴=+,
根据共面向量定理,可知与,共面.
∵∩=C,EB 平面A1CD,∴BE∥平面A1CD,故B错误.
对于C,=(-2,0,0),=(-1,-1,),
∴直线AC与直线A1D所成角的余弦值为
|cos<,>|=||==,故C正确.
对于D,由题意得,=(1,1,),平面AA1C1C的一个法向量为m=(0,0,1).
设直线CD与平面AA1C1C所成角为θ,
则直线CD与平面AA1C1C所成角的正弦值为
sin θ=||==,故D错误.
故选AC.
11.ACD 以E为坐标原点,EA,EF,ED所在直线分别为x轴、y轴、z轴建立如图D 6所示的空间直角坐标系,
图D 6
设正方形的边长为1,AE=a(0
∴cos∠AGC===-,即∠AGC=120°,
∴∠AGC的角度不会发生变化,故选项A正确.
对于B选项,=(-a,a,0),=(-a,1,1-a),=(0,1,0),=(a,0,a-1),设平面AGC的一个法向量为n=(x1,y1,z1),则
则可取n=(1,1,-1),
设平面ACB的一个法向量为p=(x2,y2,z2),则
则可取p=(1-a,0,a),
设二面角G-AC-B的大小为β,则由图D 1-6并结合n与p的方向可得,
cos β=cos
当0
∴当a∈(0,]时,cos β随着a的增大而减小,
又cos β>0,β在此时为锐角.
故二面角G-AC-B随着a的增大而增大.
同理,当
对于C选项,易知平面ABFG的一个法向量为m=(0,0,1),设AC与平面ABFG所成的角为α,
显然与m的夹角为锐角,则sin α=cos<,m>=====,
∵a∈(0,1),∴y=a+单调递减,则sin α随着a的增大而减小,∴AC与平面ABFG所成角变小,故选项C正确.
对于D选项,设与所成的角为θ,=(-a,1,1-a),=(0,1,0),
∴cos θ===,显然θ为锐角,
而y=2a2-2a+2的对称轴为直线a=,且a∈(0,1),
∴随着a的增大y=2a2-2a+2先减小后增大,则随着a的增大cos θ先增大后减小,即AC与EF所成的角先变小后变大,故选项D正确.
12. 依题意建立如图D 7所示的空间直角坐标系,则B (2,2,0),C (-2,2,0),P (0,0,6).
图D 7
由题意得M (0,0,3),N (0,,2),则=(0,,-1).
于是||==.
故M到△PBC的重心N的距离为.
13.-1 由A,B,C,M四点共面可知x+2x+4=1,∴x=-1.∴A(0,0,1),C(-1,,2),∴=(1,,1),=(-1,,1),∴cos<,>==,即与的夹角为.
14. 在Rt△ABC中,由题意知,BC=5,AD=,BD=,CD=,即在四面体AB'C D中,AD=,=,CD=,=3,AC=4,在△中,由三角形的三边关系可知,<<5,
在△中,若∠=90°,则==5,矛盾,
故∠=90°,此时==,
在△中,2+2=DC2,所以∠=90°.
此时∠AD,∠ADC,∠DC,∠AC为直角,满足四面体ACD为一个鳖臑.
如图D 8,在长、宽、高分别为,,的长方体中作出四面体ADC,以D为坐标原点建立空间直角坐标系,
图D 8
则D(0,0,0),A(0,0,),C(,,0),(,0,0),=(0,0,),=(,,0),=(,0,-),
=(0,-,0).
设向量m=(x1,y1,z1)为平面DAC的法向量,向量n=(x2,y2,z2)为平面AC的法向量,
则取x1=,可得平面DAC的一个法向量为m=(,-,0),同理可得平面AC的一个法向量为n=(1,0,),
所以cos
所以平面AC与平面DAC夹角的余弦值是.
15.连接AC,∵=+=+=+(-)=+[-(+)]=-++,
∴=-a+b+c.
∵||2=(-a+b+c)2=(|a|2+|b|2+|c|2-2a·b-2a·c+2b·c)=×(22+22+32-0-2×
2×3×cos 60°+2×2×3×cos 60°)=,∴||=.
16.由题意知,PA,AB,AD两两垂直,以{,,}为正交基底建立如图D 9所示的空间直角坐标系Axyz,
图D 9
则A(0,0,0),B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,2).
(1)易知是平面PAB的一个法向量,=(0,2,0).
易得=(1,1,-2),=(0,2,-2).
设平面PCD的一个法向量为m=(x,y,z),
则即令y=1,得z=1,x=1,所以m=(1,1,1)是平面PCD的一个法向量.
因为cos<,m>==,
所以平面PAB与平面PCD夹角的余弦值为.
(2)=(-1,0,2),设Q为直线PB上一点,且=λ=(-λ,0,2λ).连接QC,易得=(-1,1,0),=(0,-1,0),则=+=(-λ,-1,2λ),
则点Q到直线CD的距离d==,因为λ2+λ+=(λ+)2+≥,所以d≥,所以异面直线PB与CD之间的距离为.
17.取AD的中点O,连接PO,BO,∵PA=PD,∴PO⊥AD.∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴PO⊥平面ABCD.∵四边形ABCD为菱形,∠BCD=60°,∴OB⊥AD.以O为坐标原点,建立如图D 10所示的空间直角坐标系Oxyz,
图D 10
则A(1,0,0),B(0,,0),D(-1,0,0),E(-1,,0),P(0,0,1),C(-2,,0).
(1)=(-2,0,0),=(0,,-1),
∴·=(-2,0,0)·(0,,-1)=0,
∴⊥,∴AD⊥PB.
(2)设Q(x,y,z),则=(x,y,z-1).
∵=λ,∴=λ.
∵=(-2,,-1),∴
在平面DEQ中,=(0,,0),=(x+1,y,z)=(1-2λ,λ,1-λ).
设平面DEQ的一个法向量为n=(x1,y1,z1),
由得
令x1=1-λ,可得n=(1-λ,0,2λ-1)是平面DEQ的一个法向量.又PA∥平面DEQ,=(1,0,-1),∴·n=0,即1-λ-(2λ-1)=0,解得λ=.∴当λ=时,PA∥平面DEQ.
18.(1)∵PO⊥平面ABCD,AC 平面ABCD,
∴PO⊥AC,又AC⊥BD,PO∩BD=O,∴AC⊥平面POD,又PD 平面POD,∴PD⊥AC.
(2)如图D 11,以O为坐标原点,分别以,,为x,y,z轴正方向,建立空间直角坐标系Oxyz,
图D 11
则B(4,0,0),C(0,8,0),D(-4,0,0),P(0,0,2),∴=(4,0,-2),=(0,8,-2),=(-4,0,-2).
设m=(a,b,c)为平面PBC的法向量,则即
令c=4,则平面PBC的一个法向量为m=(2,1,4),设直线PD与平面PBC所成角为θ,则sin θ=|cos<,m>|=||==.
19.(1)如题图(2),∵CD⊥AD,CD⊥BD,AD∩BD=D,AD,BD 平面ABD,∴CD⊥平面ABD.
∵AB 平面ABD,∴CD⊥AB.
又M,E分别为AC,BC的中点,∴ME∥AB,∴CD⊥ME.
(2)方案一 选①,在题图(1)所示的△ABC中,由tan 2B=-=,解得tan B=2或tan B=-(舍去).
设AD=CD=x,在Rt△ABD中,tan B===2,
解得x=2,∴BD=1.
以点D为坐标原点,直线DB,DC,DA分别为x轴、y轴、z轴建立如图D 12 所示的空间直角坐标系,
图D 12
则B(1,0,0),C(0,2,0),A(0,0,2),M(0,1,1),E(,1,0),则=(-1,1,1).
设N(0,a,0),0≤a≤2,则=(-,a-1,0).
∵EN⊥BM,∴·=0,
即(-,a-1,0)·(-1,1,1)=0,∴a=,∴N(0,,0),
∴当DN=(即N是CD上靠近点D的一个四等分点)时,EN⊥BM.
设平面BNM的一个法向量为n=(x,y,z),=(-1,,0),
由得令x=1,则n=(1,2,-1).
取平面BNC的一个法向量m=(0,0,1),则cos
又二面角M-BN-C的平面角为锐角,
∴二面角M-BN-C的余弦值为.
方案二 选②,在题图(1)所示的△ABC中,设=λ,则=+=+λ(-)=(1-λ)+λ,又=+,故λ=,即BD=1.
下同选条件①.
方案三 选③,在题图(1)所示的△ABC中,设BD=x(0
又∠BDC=90°,∴S△BCD=x(3-x),
∴VA-BCD=AD·S△BCD=(3-x)·x(3-x)=,化简得(x-1)2(x-4)=0,解得x=1或x=4(舍去),故BD=1.
下同选条件①.
