选择性必修第一册苏教版-第3章-单元测试卷(含解析)
文档属性
| 名称 | 选择性必修第一册苏教版-第3章-单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 154.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-07 11:14:15 | ||
图片预览




文档简介
第3章 圆锥曲线与方程
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若点P到直线x=-1的距离比到点(2,0)的距离小1,则点P的轨迹是 ( )
A.圆 B.椭圆 C.双曲线 D.抛物线
2.若双曲线-=1的一条渐近线经过点(3,-4),则此双曲线的离心率为 ( )
A. B. C. D.
3.双曲线-=1(mn≠0)的离心率为2,有一个焦点与抛物线y2=4x的焦点重合,则mn的值为 ( )
A. B. C. D.
4.过抛物线y2=8x的焦点,作倾斜角为45°的直线,则被抛物线截得的弦长为 ( )
A.8 B.16 C.32 D.64
5.已知F1,F2为椭圆+=1(a>b>0)的两个焦点,过点F2作椭圆的弦AB,若△AF1B的周长为16,椭圆的离心率e=,则椭圆的方程是 ( )
A.+=1 B.+=1
C.+=1 D.+=1
6.已知F是抛物线y=x2的焦点,P是该抛物线上的动点,则线段PF中点的轨迹方程是 ( )
A.x2=2y-1 B.x2=2y-
C.x2=y- D.x2=2y-2
7.已知A,B为双曲线E的左、右顶点,点M在E上,△ABM为等腰三角形,且顶角为120°,则E的离心率为 ( )
A. B.2 C. D.
8.画法几何的创始人——法国数学家加斯帕尔·蒙日发现:与椭圆相切的两条垂直切线的交点的轨迹是以椭圆中心为圆心的圆.我们通常把这个圆称为该椭圆的蒙日圆.如图1,已知椭圆C:+=1(a>b>0)的蒙日圆方程为x2+y2=a2+b2,椭圆C的离心率为,M为蒙日圆上的一个动点,过点M作椭圆C的两条切线,与蒙日圆分别交于P,Q两点,则△MPQ面积的最大值为 ( )
图1
A.3b2 B.2b2 C. D.6b2
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知双曲线C过点(3,)且渐近线为y=±x,则下列结论正确的是 ( )
A.C的方程为-y2=1 B.C的离心率为
C.曲线y=ex-2-1经过C的一个焦点 D.直线x-y-1=0与C有两个公共点
10.已知双曲线C:-y2=1(a>0),若圆(x-2)2+y2=1与双曲线C的渐近线相切,则 ( )
A.双曲线C的实轴长为6
B.双曲线C的离心率e=
C.点P为双曲线上任意一点,若点P到C的两条渐近线的距离分别为d1,d2,则d1d2=
D.直线y=k1x+m与C交于A,B两点,点D为弦AB的中点,若OD(O为坐标原点)的斜率为k2,则k1k2=
11.设椭圆的方程为+=1,斜率为k的直线不经过原点O,而且与椭圆相交于A,B两点,M为线段AB的中点,下列结论正确的是 ( )
A.直线AB与OM垂直
B.若点M坐标为(1,1),则直线方程为2x+y-3=0
C.若直线方程为y=x+1,则点M坐标为(,)
D.若直线方程为y=x+2,则AB=
三、填空题:本题共3小题,每小题5分,共15分.
12.已知F为抛物线C:y2=x的焦点,点A,B在抛物线上,且分别位于x轴的上、下两侧,若△BFO的面积是(O为坐标原点),且·=12,则直线AB的斜率是 .
13.双曲线E:-=1(a>0,b>0)的一条渐近线的方程为y=x,则该双曲线的离心率为 ,若E上的点A满足AF2⊥F1F2,其中F1,F2分别是E的左、右焦点,则sin∠AF1F2= .
14.国家体育场(鸟巢)的钢结构鸟瞰结构图如图2所示,内外两圈的钢骨架是离心率相同的椭圆,将其平面图放入适当的平面直角坐标系中,如图3,若由外层椭圆长轴一端点A和短轴一端点B分别向内层椭圆引切线AC,BD,且两切线斜率之积等于-,则椭圆的离心率为 .
图2 图3
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)已知抛物线C:y2=2px(p>0)的焦点F的坐标为(1,0),过焦点F的直线l交抛物线C于A,B两点.
(1)求抛物线C的方程;
(2)记抛物线的准线与x轴交于点E,若·=40,求直线l的方程.
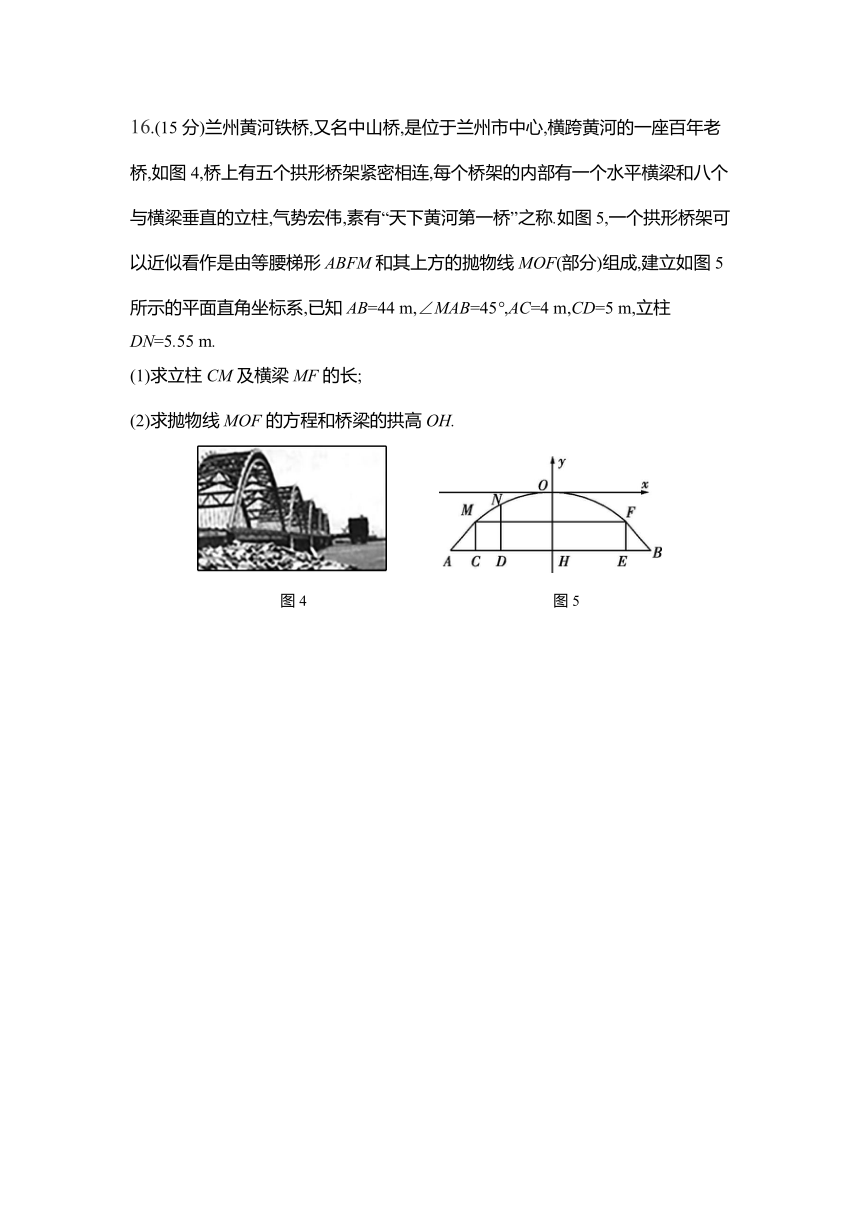
16.(15分)兰州黄河铁桥,又名中山桥,是位于兰州市中心,横跨黄河的一座百年老桥,如图4,桥上有五个拱形桥架紧密相连,每个桥架的内部有一个水平横梁和八个与横梁垂直的立柱,气势宏伟,素有“天下黄河第一桥”之称.如图5,一个拱形桥架可以近似看作是由等腰梯形ABFM和其上方的抛物线MOF(部分)组成,建立如图5所示的平面直角坐标系,已知AB=44 m,∠MAB=45°,AC=4 m,CD=5 m,立柱DN=5.55 m.
(1)求立柱CM及横梁MF的长;
(2)求抛物线MOF的方程和桥梁的拱高OH.
图4 图5
17.(15分)在①点M为椭圆C的上顶点时,△MF1F2面积为4,②椭圆C过点(,),③离心率e=这三个条件中任选一个,补充在下面问题的横线处,并解决下面两个问题.
设椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,直线l:y=x+m与椭圆C交于A,B两点,以AB为底边作等腰三角形,顶点为P(-3,2).已知椭圆C的短轴长为4, .
(1)求椭圆C的方程;
(2)求m的值和△PAB的面积.
注:若选择多个条件分别解答,则按第一个解答计分.
18.(17分)已知双曲线的方程为2x2-y2=2.
(1)求以点A(2,2)为中点的双曲线的弦所在的直线方程.
(2)过点B(1,1)能否作直线l,使l与所给双曲线交于Q1,Q2两点,且点B是弦Q1Q2的中点 如果存在,求出直线l的方程;如果不存在,请说明理由.
19.(17分)已知椭圆E: +=1(a>b>0)的左、右焦点分别为F1(-1,0),F2(1,0),过F1且斜率为的直线与椭圆的一个交点在x轴上的射影恰好为F2,
(1)求椭圆E的方程.
(2)如图6,下顶点为A,过点B(0,2)作一条与y轴不重合的直线,该直线交椭圆E于C,D两点,直线AD,AC分别交x轴于点H,G.求证:△ABG与△AOH的面积之积为定值,并求出该定值.
图6
第3章 圆锥曲线与方程
1.D 点P到直线x=-1的距离比到点(2,0)的距离小1,即点P到直线x=-2的距离与到点(2,0)的距离相等,根据抛物线的定义可知,点P的轨迹是抛物线.
2.D 由已知可得双曲线的渐近线方程为y=±x,点(3,-4)在渐近线上,
∴=,又a2+b2=c2,∴c2=a2+a2=a2,∴e==.
3.A 抛物线y2=4x的焦点为F(1,0),
故双曲线-=1中,m>0,n>0且m+n=c2=1 ①,e===2 ②,
联立①②,解得m=,n=.故mn=.
4.B 抛物线中2p=8,p=4,则焦点坐标为(2,0),过焦点且倾斜角为45°的直线方程为y=x-2,由得x2-12x+4=0,则x1+x2=12(x1,x2为直线与抛物线两个交点的横坐标).从而弦长为x1+x2+p=12+4=16.
5.D 由椭圆的定义知AF1+BF1+AB=4a=16,∴a=4.
又e==,∴c=2,∴b2=42-(2)2=4,
∴椭圆的方程为+=1.
6.A 焦点为F(0,1),设点P(p,q),则p2=4q.设点Q(x,y)是线段PF的中点,则x=,y=,即p=2x,q=2y-1,代入p2=4q得,(2x)2=4(2y-1),即x2=2y-1.
7.D 设双曲线方程为-=1(a>0,b>0),不妨设点M在双曲线的右支上,
图D 1
如图D 1所示,AB=BM=2a,∠MBA=120°,过点M作MH⊥x轴于点H,
则∠MBH=60°,BH=a,MH=a,所以M(2a,a).
将点M的坐标代入双曲线方程-=1,得a=b,所以e=.
8.A 由“蒙日圆”的定义可知,MP⊥MQ,则PQ为蒙日圆的直径,连接OM,∴OM=,则PQ=2OM=2,
设MP=m,MQ=n,∴m2+n2=PQ2=4(a2+b2),
又m2+n2≥2mn(当且仅当m=n时取等号),
∴4(a2+b2)≥2mn,即mn≤2(a2+b2),
∴S△MPQ=mn≤·2(a2+b2)=a2+b2.
∵e==,∴a2=2c2=2(a2-b2),即a2=2b2,∴a2+b2=3b2,故△MPQ面积的最大值为3b2.
9.AC ∵双曲线的渐近线为y=±x,∴设双曲线C的方程为-y2=λ(λ≠0),又该双曲线过点(3,),代入方程得λ=1,故选项A正确.易知双曲线C的离心率e为,故选项B错误.y=ex-2-1经过双曲线C的右焦点(2,0),故选项C正确.联立直线和双曲线C的方程,消去x得y2-2y+2=0,∵Δ=0,故该直线与双曲线C有一个公共点,所以选项D错误.
10.BCD 由题意知C的渐近线方程为x±ay=0,因为圆与渐近线相切,所以=1,解得a=,所以实轴长为2,c=2,所以e==,故A错误,B正确;设P(x0,y0),
所以d1=,d2=,所以d1d2=·==,故C正确;
设A(x1,y1),B(x2,y2),则D(,),联立直线与双曲线C的方程,消去y得(1-3)x2-6k1mx-(3m2+3)=0,所以x1+x2=,y1+y2=,则k2==,即k1k2=,
故D正确.故选BCD.
11.BD 假设直线与椭圆交于椭圆的左端点A(-,0)和上顶点B(0,2),显然△ABO不是等腰直角三角形,AB与OM显然是不垂直的.故A错误.
设直线方程为y=kx+b(b≠0).联立直线与椭圆的方程,消去y得,(2+k2)x2+2kbx+b2-4=0.
设点A(x1,y1),B(x2,y2),则x1+x2=-,y1+y2=k(x1+x2)+2b=-+2b=.
故点M的坐标为(-,).
对于B,点M(1,1),则解得即所求直线方程为2x+y-3=0.故B正确.
对于C,若直线方程为y=x+1,即k=1,b=1,则M点坐标为(-,),故C错误.
对于D,若直线方程为y=x+2,即k=1,b=2,
AB=|x1-x2|==×=.故D正确.
12.- 设A(x1,y1),B(x2,y2),由抛物线y2=x得F(,0),而S△BFO=××(-y2)=,得y2=-4,则x2=16,由·=x1x2+y1y2=16x1-4y1=12,得4x1-y1=3,又=x1,结合y1>0,解得y1=1,x1=1,所以直线AB的斜率为=-.
13. 由题意得=,则b=a,c2=a2+b2=3a2,所以c=a,所以双曲线的离心率e==.在-=1中,令x=c,得y=±=±2a,所以不妨设A(a,2a),则AF2=2a,由AF1-AF2=2a,得AF1=4a,所以sin∠AF1F2==.
14. 设内层椭圆方程为+=1(a>b>0).
∵内外层椭圆的离心率相同,∴外层椭圆可设成+=1(m>1).
设切线AC的方程为y=k1(x+ma),
与+=1联立得,(b2+a2)x2+2ma3x+m2a4-a2b2=0,
由Δ=0,得=·,同理=(m2-1),
∴·==(-)2,即=,
因此e====.
15.(1)由题意得=1,即p=2,
所以抛物线C的方程为y2=4x.
(2)由题意,知E(-1,0),直线l的斜率一定不为0,所以可设直线l的方程为x=my+1,点A(x1,y1),B(x2,y2).
联立直线l和抛物线C的方程得消元得y2-4my-4=0,则y1+y2=4m,y1y2=-4,所以x1x2=(my1+1)(my2+1)=1,x1+x2=m(y1+y2)+2=4m2+2,
所以·=(x1+1,y1)·(x2+1,y2)=x1x2+1+x1+x2+y1y2=1+1+4m2+2-4=4m2=40,
解得m=或m=-.
故直线l的方程为x+y-1=0或x-y-1=0.
16.(1)由题意知,∠MAB=45°,AC=4 m,则CM=4 m,因为四边形ABFM是等腰梯形,由对称性可知,AH=HB=AB=22 m,AC=BE=4 m,CH=AH-AC=18 m,
所以MF=2CH=36 m.
(2)由(1)知点M的横坐标为-18,N的横坐标为-(18-5)=-13.
设M,N的纵坐标分别为y1,y2,
由题图可知|y1-y2|=|5.55-4|=1.55.
设抛物线MOF的方程为x2=-2py,p>0,x∈[-18,18].
将点M,N的坐标代入抛物线方程,得
两式相减得2p(y2-y1)=182-132=155,
解得2p=100,故抛物线方程为x2=-100y,x∈[-18,18].
因此当x=-18时,y=-×(-18)2=-3.24,
故|y1|=3.24 m,
所以桥梁的拱高OH=3.24+4=7.24 m.
17.(1)由已知可得2b=4,解得b=2,故椭圆C的方程为+=1.
若选择①,则×2c×b=bc=2c=4,解得c=2,故a2=b2+c2=12,
故椭圆C的方程为+=1.
若选择②,则+=1,解得a2=12,
故椭圆C的方程为+=1.
若选择③,则e=====,解得a2=12,
故椭圆C的方程为+=1.
(2)设A(x1,y1),B(x2,y2),
由可得4x2+6mx+3m2-12=0 (*),
由Δ=(6m)2-4×4×(3m2-12)>0,可得-4且x1+x2=-,x1x2=.
设线段AB的中点为H(x0,y0),
则x0==-,y0=x0+m=,即H(-,),
因为-4因为△PAB是以AB为底边的等腰三角形,
所以PH⊥AB,即PH⊥l,
又直线l的斜率k=1,所以kPH=-1,即=-1,
解得m=2∈(-4,4),
此时方程(*)化为4x2+12x=0,解得x1=0,x2=-3,
AB=|x1-x2|=×|0-(-3)|=3,
此时H(-,),
故PH==,
故S△PAB=×AB×PH=×3×=.
综上,m=2,△PAB的面积为.
18.(1)设以点A(2,2)为中点的弦的两端点分别为P1(x1,y1),P2(x2,y2),则有x1+x2=4,y1+y2=4,x1≠x2.由P1,P2在双曲线上,得2-=2,2-=2,两式相减,得2(x1+x2)(x1-x2)-(y1+y2)(y1-y2)=0.
则2×4(x1-x2)-4(y1-y2)=0,即=2,
故中点弦所在的直线方程为y-2=2(x-2),即2x-y-2=0.
(2)假设直线l存在,可利用(1)中的方法求出直线l的方程为y-1=2(x-1),即2x-y-1=0.
联立方程消去y,得2x2-4x+3=0.
因为Δ=(-4)2-4×2×3=-8<0,所以方程无实数根,因此直线l与双曲线无交点.
故满足条件的直线l不存在.
19.(1)过F1(-1,0)且斜率为的直线方程为y=(x+1),
令x=1,得y=,由题意可得解得
所以椭圆E的方程为+y2=1.
(2)由题意知,直线BC的斜率存在,设直线BC的方程为y=kx+2,D(x1,y1),C(x2,y2),
将y=kx+2代入+y2=1,消去y得(1+2k2)x2+8kx+6=0,
所以x1+x2=,x1x2=,
由Δ=16k2-24>0,得k2>,
所以y1+y2=k(x1+x2)+4=,
y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=.
直线AD的方程为y=x-1,令y=0,解得x=,
则H(,0);
直线AC的方程为y=x-1,令y=0,解得x=,则G(,0).
所以S△ABG·S△AOH=×3×||××1×||=||=||=||=×||=×=.
所以△ABG与△AOH的面积之积为定值,该定值为.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若点P到直线x=-1的距离比到点(2,0)的距离小1,则点P的轨迹是 ( )
A.圆 B.椭圆 C.双曲线 D.抛物线
2.若双曲线-=1的一条渐近线经过点(3,-4),则此双曲线的离心率为 ( )
A. B. C. D.
3.双曲线-=1(mn≠0)的离心率为2,有一个焦点与抛物线y2=4x的焦点重合,则mn的值为 ( )
A. B. C. D.
4.过抛物线y2=8x的焦点,作倾斜角为45°的直线,则被抛物线截得的弦长为 ( )
A.8 B.16 C.32 D.64
5.已知F1,F2为椭圆+=1(a>b>0)的两个焦点,过点F2作椭圆的弦AB,若△AF1B的周长为16,椭圆的离心率e=,则椭圆的方程是 ( )
A.+=1 B.+=1
C.+=1 D.+=1
6.已知F是抛物线y=x2的焦点,P是该抛物线上的动点,则线段PF中点的轨迹方程是 ( )
A.x2=2y-1 B.x2=2y-
C.x2=y- D.x2=2y-2
7.已知A,B为双曲线E的左、右顶点,点M在E上,△ABM为等腰三角形,且顶角为120°,则E的离心率为 ( )
A. B.2 C. D.
8.画法几何的创始人——法国数学家加斯帕尔·蒙日发现:与椭圆相切的两条垂直切线的交点的轨迹是以椭圆中心为圆心的圆.我们通常把这个圆称为该椭圆的蒙日圆.如图1,已知椭圆C:+=1(a>b>0)的蒙日圆方程为x2+y2=a2+b2,椭圆C的离心率为,M为蒙日圆上的一个动点,过点M作椭圆C的两条切线,与蒙日圆分别交于P,Q两点,则△MPQ面积的最大值为 ( )
图1
A.3b2 B.2b2 C. D.6b2
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知双曲线C过点(3,)且渐近线为y=±x,则下列结论正确的是 ( )
A.C的方程为-y2=1 B.C的离心率为
C.曲线y=ex-2-1经过C的一个焦点 D.直线x-y-1=0与C有两个公共点
10.已知双曲线C:-y2=1(a>0),若圆(x-2)2+y2=1与双曲线C的渐近线相切,则 ( )
A.双曲线C的实轴长为6
B.双曲线C的离心率e=
C.点P为双曲线上任意一点,若点P到C的两条渐近线的距离分别为d1,d2,则d1d2=
D.直线y=k1x+m与C交于A,B两点,点D为弦AB的中点,若OD(O为坐标原点)的斜率为k2,则k1k2=
11.设椭圆的方程为+=1,斜率为k的直线不经过原点O,而且与椭圆相交于A,B两点,M为线段AB的中点,下列结论正确的是 ( )
A.直线AB与OM垂直
B.若点M坐标为(1,1),则直线方程为2x+y-3=0
C.若直线方程为y=x+1,则点M坐标为(,)
D.若直线方程为y=x+2,则AB=
三、填空题:本题共3小题,每小题5分,共15分.
12.已知F为抛物线C:y2=x的焦点,点A,B在抛物线上,且分别位于x轴的上、下两侧,若△BFO的面积是(O为坐标原点),且·=12,则直线AB的斜率是 .
13.双曲线E:-=1(a>0,b>0)的一条渐近线的方程为y=x,则该双曲线的离心率为 ,若E上的点A满足AF2⊥F1F2,其中F1,F2分别是E的左、右焦点,则sin∠AF1F2= .
14.国家体育场(鸟巢)的钢结构鸟瞰结构图如图2所示,内外两圈的钢骨架是离心率相同的椭圆,将其平面图放入适当的平面直角坐标系中,如图3,若由外层椭圆长轴一端点A和短轴一端点B分别向内层椭圆引切线AC,BD,且两切线斜率之积等于-,则椭圆的离心率为 .
图2 图3
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)已知抛物线C:y2=2px(p>0)的焦点F的坐标为(1,0),过焦点F的直线l交抛物线C于A,B两点.
(1)求抛物线C的方程;
(2)记抛物线的准线与x轴交于点E,若·=40,求直线l的方程.
16.(15分)兰州黄河铁桥,又名中山桥,是位于兰州市中心,横跨黄河的一座百年老桥,如图4,桥上有五个拱形桥架紧密相连,每个桥架的内部有一个水平横梁和八个与横梁垂直的立柱,气势宏伟,素有“天下黄河第一桥”之称.如图5,一个拱形桥架可以近似看作是由等腰梯形ABFM和其上方的抛物线MOF(部分)组成,建立如图5所示的平面直角坐标系,已知AB=44 m,∠MAB=45°,AC=4 m,CD=5 m,立柱DN=5.55 m.
(1)求立柱CM及横梁MF的长;
(2)求抛物线MOF的方程和桥梁的拱高OH.
图4 图5
17.(15分)在①点M为椭圆C的上顶点时,△MF1F2面积为4,②椭圆C过点(,),③离心率e=这三个条件中任选一个,补充在下面问题的横线处,并解决下面两个问题.
设椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,直线l:y=x+m与椭圆C交于A,B两点,以AB为底边作等腰三角形,顶点为P(-3,2).已知椭圆C的短轴长为4, .
(1)求椭圆C的方程;
(2)求m的值和△PAB的面积.
注:若选择多个条件分别解答,则按第一个解答计分.
18.(17分)已知双曲线的方程为2x2-y2=2.
(1)求以点A(2,2)为中点的双曲线的弦所在的直线方程.
(2)过点B(1,1)能否作直线l,使l与所给双曲线交于Q1,Q2两点,且点B是弦Q1Q2的中点 如果存在,求出直线l的方程;如果不存在,请说明理由.
19.(17分)已知椭圆E: +=1(a>b>0)的左、右焦点分别为F1(-1,0),F2(1,0),过F1且斜率为的直线与椭圆的一个交点在x轴上的射影恰好为F2,
(1)求椭圆E的方程.
(2)如图6,下顶点为A,过点B(0,2)作一条与y轴不重合的直线,该直线交椭圆E于C,D两点,直线AD,AC分别交x轴于点H,G.求证:△ABG与△AOH的面积之积为定值,并求出该定值.
图6
第3章 圆锥曲线与方程
1.D 点P到直线x=-1的距离比到点(2,0)的距离小1,即点P到直线x=-2的距离与到点(2,0)的距离相等,根据抛物线的定义可知,点P的轨迹是抛物线.
2.D 由已知可得双曲线的渐近线方程为y=±x,点(3,-4)在渐近线上,
∴=,又a2+b2=c2,∴c2=a2+a2=a2,∴e==.
3.A 抛物线y2=4x的焦点为F(1,0),
故双曲线-=1中,m>0,n>0且m+n=c2=1 ①,e===2 ②,
联立①②,解得m=,n=.故mn=.
4.B 抛物线中2p=8,p=4,则焦点坐标为(2,0),过焦点且倾斜角为45°的直线方程为y=x-2,由得x2-12x+4=0,则x1+x2=12(x1,x2为直线与抛物线两个交点的横坐标).从而弦长为x1+x2+p=12+4=16.
5.D 由椭圆的定义知AF1+BF1+AB=4a=16,∴a=4.
又e==,∴c=2,∴b2=42-(2)2=4,
∴椭圆的方程为+=1.
6.A 焦点为F(0,1),设点P(p,q),则p2=4q.设点Q(x,y)是线段PF的中点,则x=,y=,即p=2x,q=2y-1,代入p2=4q得,(2x)2=4(2y-1),即x2=2y-1.
7.D 设双曲线方程为-=1(a>0,b>0),不妨设点M在双曲线的右支上,
图D 1
如图D 1所示,AB=BM=2a,∠MBA=120°,过点M作MH⊥x轴于点H,
则∠MBH=60°,BH=a,MH=a,所以M(2a,a).
将点M的坐标代入双曲线方程-=1,得a=b,所以e=.
8.A 由“蒙日圆”的定义可知,MP⊥MQ,则PQ为蒙日圆的直径,连接OM,∴OM=,则PQ=2OM=2,
设MP=m,MQ=n,∴m2+n2=PQ2=4(a2+b2),
又m2+n2≥2mn(当且仅当m=n时取等号),
∴4(a2+b2)≥2mn,即mn≤2(a2+b2),
∴S△MPQ=mn≤·2(a2+b2)=a2+b2.
∵e==,∴a2=2c2=2(a2-b2),即a2=2b2,∴a2+b2=3b2,故△MPQ面积的最大值为3b2.
9.AC ∵双曲线的渐近线为y=±x,∴设双曲线C的方程为-y2=λ(λ≠0),又该双曲线过点(3,),代入方程得λ=1,故选项A正确.易知双曲线C的离心率e为,故选项B错误.y=ex-2-1经过双曲线C的右焦点(2,0),故选项C正确.联立直线和双曲线C的方程,消去x得y2-2y+2=0,∵Δ=0,故该直线与双曲线C有一个公共点,所以选项D错误.
10.BCD 由题意知C的渐近线方程为x±ay=0,因为圆与渐近线相切,所以=1,解得a=,所以实轴长为2,c=2,所以e==,故A错误,B正确;设P(x0,y0),
所以d1=,d2=,所以d1d2=·==,故C正确;
设A(x1,y1),B(x2,y2),则D(,),联立直线与双曲线C的方程,消去y得(1-3)x2-6k1mx-(3m2+3)=0,所以x1+x2=,y1+y2=,则k2==,即k1k2=,
故D正确.故选BCD.
11.BD 假设直线与椭圆交于椭圆的左端点A(-,0)和上顶点B(0,2),显然△ABO不是等腰直角三角形,AB与OM显然是不垂直的.故A错误.
设直线方程为y=kx+b(b≠0).联立直线与椭圆的方程,消去y得,(2+k2)x2+2kbx+b2-4=0.
设点A(x1,y1),B(x2,y2),则x1+x2=-,y1+y2=k(x1+x2)+2b=-+2b=.
故点M的坐标为(-,).
对于B,点M(1,1),则解得即所求直线方程为2x+y-3=0.故B正确.
对于C,若直线方程为y=x+1,即k=1,b=1,则M点坐标为(-,),故C错误.
对于D,若直线方程为y=x+2,即k=1,b=2,
AB=|x1-x2|==×=.故D正确.
12.- 设A(x1,y1),B(x2,y2),由抛物线y2=x得F(,0),而S△BFO=××(-y2)=,得y2=-4,则x2=16,由·=x1x2+y1y2=16x1-4y1=12,得4x1-y1=3,又=x1,结合y1>0,解得y1=1,x1=1,所以直线AB的斜率为=-.
13. 由题意得=,则b=a,c2=a2+b2=3a2,所以c=a,所以双曲线的离心率e==.在-=1中,令x=c,得y=±=±2a,所以不妨设A(a,2a),则AF2=2a,由AF1-AF2=2a,得AF1=4a,所以sin∠AF1F2==.
14. 设内层椭圆方程为+=1(a>b>0).
∵内外层椭圆的离心率相同,∴外层椭圆可设成+=1(m>1).
设切线AC的方程为y=k1(x+ma),
与+=1联立得,(b2+a2)x2+2ma3x+m2a4-a2b2=0,
由Δ=0,得=·,同理=(m2-1),
∴·==(-)2,即=,
因此e====.
15.(1)由题意得=1,即p=2,
所以抛物线C的方程为y2=4x.
(2)由题意,知E(-1,0),直线l的斜率一定不为0,所以可设直线l的方程为x=my+1,点A(x1,y1),B(x2,y2).
联立直线l和抛物线C的方程得消元得y2-4my-4=0,则y1+y2=4m,y1y2=-4,所以x1x2=(my1+1)(my2+1)=1,x1+x2=m(y1+y2)+2=4m2+2,
所以·=(x1+1,y1)·(x2+1,y2)=x1x2+1+x1+x2+y1y2=1+1+4m2+2-4=4m2=40,
解得m=或m=-.
故直线l的方程为x+y-1=0或x-y-1=0.
16.(1)由题意知,∠MAB=45°,AC=4 m,则CM=4 m,因为四边形ABFM是等腰梯形,由对称性可知,AH=HB=AB=22 m,AC=BE=4 m,CH=AH-AC=18 m,
所以MF=2CH=36 m.
(2)由(1)知点M的横坐标为-18,N的横坐标为-(18-5)=-13.
设M,N的纵坐标分别为y1,y2,
由题图可知|y1-y2|=|5.55-4|=1.55.
设抛物线MOF的方程为x2=-2py,p>0,x∈[-18,18].
将点M,N的坐标代入抛物线方程,得
两式相减得2p(y2-y1)=182-132=155,
解得2p=100,故抛物线方程为x2=-100y,x∈[-18,18].
因此当x=-18时,y=-×(-18)2=-3.24,
故|y1|=3.24 m,
所以桥梁的拱高OH=3.24+4=7.24 m.
17.(1)由已知可得2b=4,解得b=2,故椭圆C的方程为+=1.
若选择①,则×2c×b=bc=2c=4,解得c=2,故a2=b2+c2=12,
故椭圆C的方程为+=1.
若选择②,则+=1,解得a2=12,
故椭圆C的方程为+=1.
若选择③,则e=====,解得a2=12,
故椭圆C的方程为+=1.
(2)设A(x1,y1),B(x2,y2),
由可得4x2+6mx+3m2-12=0 (*),
由Δ=(6m)2-4×4×(3m2-12)>0,可得-4
设线段AB的中点为H(x0,y0),
则x0==-,y0=x0+m=,即H(-,),
因为-4
所以PH⊥AB,即PH⊥l,
又直线l的斜率k=1,所以kPH=-1,即=-1,
解得m=2∈(-4,4),
此时方程(*)化为4x2+12x=0,解得x1=0,x2=-3,
AB=|x1-x2|=×|0-(-3)|=3,
此时H(-,),
故PH==,
故S△PAB=×AB×PH=×3×=.
综上,m=2,△PAB的面积为.
18.(1)设以点A(2,2)为中点的弦的两端点分别为P1(x1,y1),P2(x2,y2),则有x1+x2=4,y1+y2=4,x1≠x2.由P1,P2在双曲线上,得2-=2,2-=2,两式相减,得2(x1+x2)(x1-x2)-(y1+y2)(y1-y2)=0.
则2×4(x1-x2)-4(y1-y2)=0,即=2,
故中点弦所在的直线方程为y-2=2(x-2),即2x-y-2=0.
(2)假设直线l存在,可利用(1)中的方法求出直线l的方程为y-1=2(x-1),即2x-y-1=0.
联立方程消去y,得2x2-4x+3=0.
因为Δ=(-4)2-4×2×3=-8<0,所以方程无实数根,因此直线l与双曲线无交点.
故满足条件的直线l不存在.
19.(1)过F1(-1,0)且斜率为的直线方程为y=(x+1),
令x=1,得y=,由题意可得解得
所以椭圆E的方程为+y2=1.
(2)由题意知,直线BC的斜率存在,设直线BC的方程为y=kx+2,D(x1,y1),C(x2,y2),
将y=kx+2代入+y2=1,消去y得(1+2k2)x2+8kx+6=0,
所以x1+x2=,x1x2=,
由Δ=16k2-24>0,得k2>,
所以y1+y2=k(x1+x2)+4=,
y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=.
直线AD的方程为y=x-1,令y=0,解得x=,
则H(,0);
直线AC的方程为y=x-1,令y=0,解得x=,则G(,0).
所以S△ABG·S△AOH=×3×||××1×||=||=||=||=×||=×=.
所以△ABG与△AOH的面积之积为定值,该定值为.
