湘教版数学八年级下册(新) 课件:2.6.2《菱形的判定》(共28张PPT)
文档属性
| 名称 | 湘教版数学八年级下册(新) 课件:2.6.2《菱形的判定》(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 418.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-14 00:00:00 | ||
图片预览






文档简介
课件28张PPT。 菱形的判定菱形 复习与回顾:1.菱形的定义:2.菱形的性质:有一组邻边相等的平行四边形叫做菱形。?
?对边平行
四边相等对角相等对角线互相平分、互相垂直且平分每一组对角
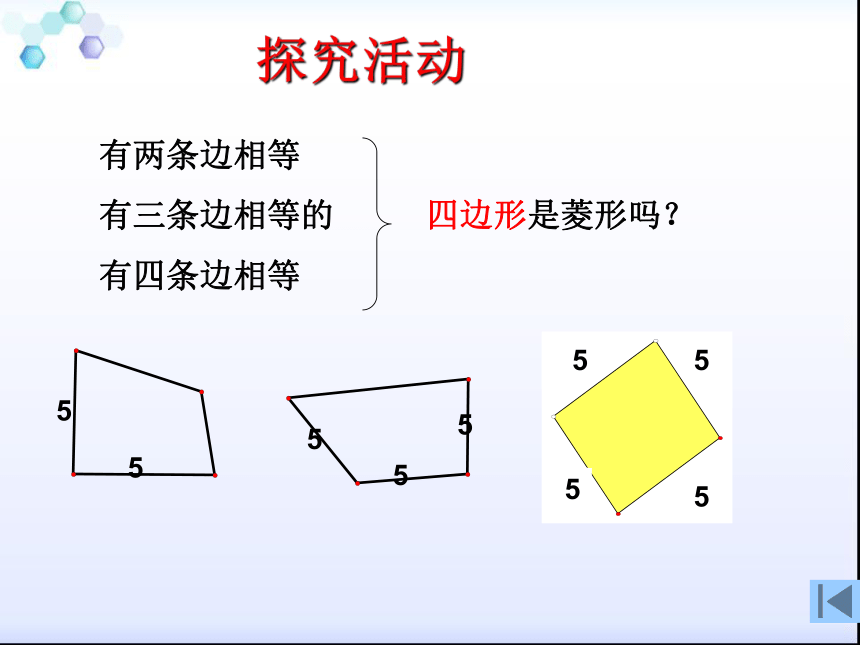
想一想如果一个四边形是平行四边形,则只要再有什么条件就可以判定它是一个菱形?根据什么?有一组邻边相等的平行四边形叫做菱形.根据定义得:探究活动有两条边相等
有三条边相等的 四边形是菱形吗?
有四条边相等
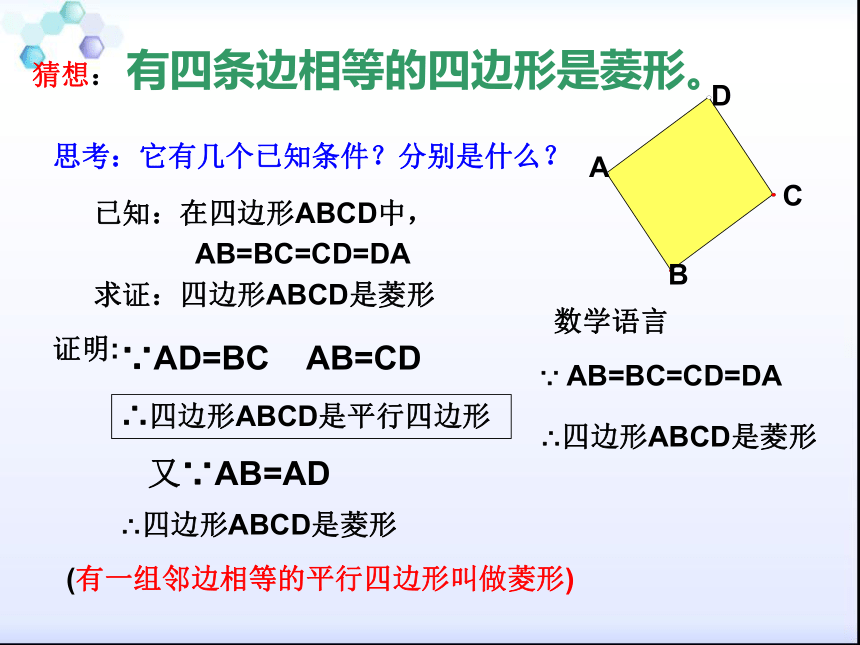
思考:它有几个已知条件?分别是什么?猜想: 有四条边相等的四边形是菱形。数学语言∴四边形ABCD是平行四边形已知:在四边形ABCD中,AB=BC=CD=DA求证:四边形ABCD是菱形证明:∴四边形ABCD是菱形(有一组邻边相等的平行四边形叫做菱形)∵ AB=BC=CD=DA∴四边形ABCD是菱形∵AD=BC AB=CD又∵AB=AD画一画先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?你根据什么方法能判定是菱形吗?有四条边相等的四边形是菱形。O∵在四边形ABCD中,
AB=BC=CD=DA
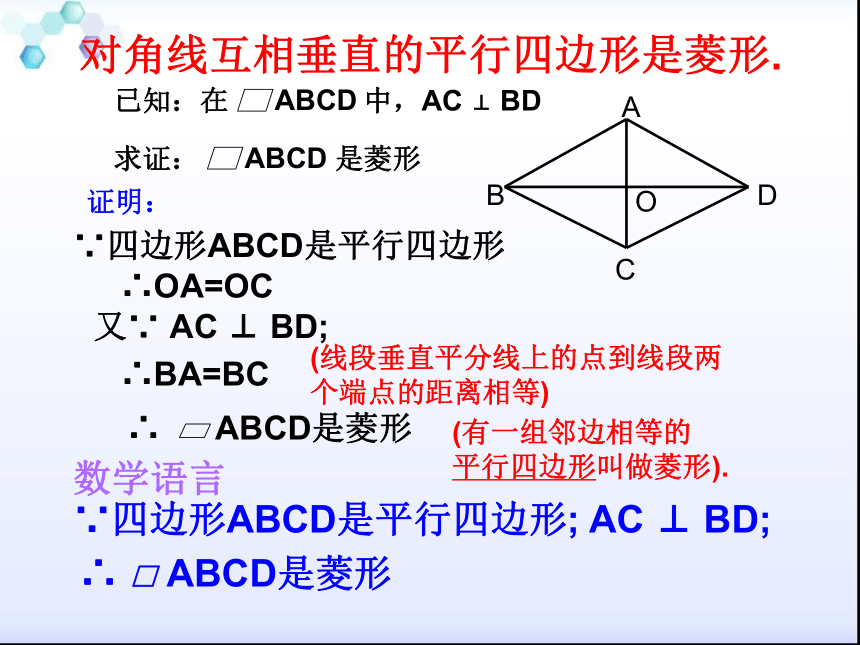
∴四边形ABCD是菱形.思考 用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?猜想对角线互相垂直的平行四边形是菱形.对角线互相垂直的平行四边形是菱形.证明:∴ ABCD是菱形又∵ AC ⊥ BD;∵四边形ABCD是平行四边形∴OA=OC∴BA=BC数学语言∵四边形ABCD是平行四边形; AC ⊥ BD;∴ □ ABCD是菱形O(线段垂直平分线上的点到线段两个端点的距离相等)(有一组邻边相等的
平行四边形叫做菱形).归纳菱形常用的判定方法:有一组邻边相等的平行四边形是菱形.对角线互相垂直的平行四边形是菱形.有四条边相等的四边形是菱形.如图, ABCD的两条对角线AC、BD相交于点O,AB= 5 ,AC=8,DB=6
求证:四边形ABCD是菱形.∴四边形ABCD是菱形.∴OA=OC=4
OB=OD=3证明:∵ AB=5 ∴AC⊥BD∴ ∠AOB=(1)∵ 四边形ABCD是平行四边形(平行四边形的对角线互相平分)(对角线互相垂直的平行四边形是菱形). 判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.√ ╳ ╳ ╳ □ABCD的对角线AC与BD相交于点O, (1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。菱矩矩菱请你动脑筋把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?ACDB思考:例题解析:已知: ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F 求证:四边形AFCE是菱形。分析: (1)利用定义判定
(2) 由已知可知
OA=OC,EF⊥AC.
(3)利用四边相等,你会吗? 分析:四边形AFCE是菱形AE=EC=CF=FAAE=ECAF=CFAE=AFEF 垂直平分AC∠1= ∠2∠1= ∠3∠2= ∠3AE∥FC四边形ABCD 是平行四边形AF=CF EF ⊥AC123 二.已知:如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD,PD、PC相交于点P。
(1)猜想:四边形PCOD是什么特殊的四边形? (2)试证明你的猜想。 (3)? PO与CD有怎样的关系?
四边形PCOD是菱形。PO与CD互相垂直且平分如图4-48,CD为Rt△ABC斜边AB上的高,∠BAC的平分线交CD于E,交BC于F,FG⊥AB于G.求证:四边形EGFC为菱形.
一组邻边相等对角线互相垂直四条边相等五种判定方法四边形小结:菱形的判定方法: 作 业5、6四边形1、26矩形与菱形有一角是直角的平行四边形叫做矩形.有一组邻边相等的平行四边形叫做菱形.平行四边形的性质性质边角对角线四个角都是直角相等互相垂直且平分每一组对角判定有一角是直角的平行四边形对角线相等的平行四边形三个角都是直角的四边形有一组邻边相等的平行四边形对角线互相垂直的平行四边形四条边都相等的四边形四条边都相等如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,
证明:CE⊥DF.例:如图,Rt△ABC中,∠ACB=900,∠BAC=600,DE垂直平分BC,垂足为D,交AB于E,又点F在DE的延长线上,且AF=CE,求证:四边形ACEF是菱形。例:如下图在△ABC中,∠BAC=90°,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于C,EF⊥BC于F,四边形AEFG是菱形吗?如图,AD∥BC,BD垂直平分AC,四边形ABCD一定是菱形吗?若是,请说明理由。思考题:┐) 12 (提示: △AOD≌△COB(角边角)AD=BC
如图,已知AD平分∠BAC,DE//AC,
DF//AB,AE=5.
(1)判断四边形AEDF的形状?
(2)它的周长为多少?
练习:如图在菱形ABCD中,CE⊥AB,CF⊥AD.
则CE与CF相等吗?说明理由。
BE与DF呢?已知,如图, ∠ ABC中, ∠ ACB= 900,BF平分∠ ABC,CD垂直于AB于D,和BF交于点G , GE ∥ CA.
求证:CE和FG互相垂直平分。
?对边平行
四边相等对角相等对角线互相平分、互相垂直且平分每一组对角
想一想如果一个四边形是平行四边形,则只要再有什么条件就可以判定它是一个菱形?根据什么?有一组邻边相等的平行四边形叫做菱形.根据定义得:探究活动有两条边相等
有三条边相等的 四边形是菱形吗?
有四条边相等
思考:它有几个已知条件?分别是什么?猜想: 有四条边相等的四边形是菱形。数学语言∴四边形ABCD是平行四边形已知:在四边形ABCD中,AB=BC=CD=DA求证:四边形ABCD是菱形证明:∴四边形ABCD是菱形(有一组邻边相等的平行四边形叫做菱形)∵ AB=BC=CD=DA∴四边形ABCD是菱形∵AD=BC AB=CD又∵AB=AD画一画先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?你根据什么方法能判定是菱形吗?有四条边相等的四边形是菱形。O∵在四边形ABCD中,
AB=BC=CD=DA
∴四边形ABCD是菱形.思考 用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?猜想对角线互相垂直的平行四边形是菱形.对角线互相垂直的平行四边形是菱形.证明:∴ ABCD是菱形又∵ AC ⊥ BD;∵四边形ABCD是平行四边形∴OA=OC∴BA=BC数学语言∵四边形ABCD是平行四边形; AC ⊥ BD;∴ □ ABCD是菱形O(线段垂直平分线上的点到线段两个端点的距离相等)(有一组邻边相等的
平行四边形叫做菱形).归纳菱形常用的判定方法:有一组邻边相等的平行四边形是菱形.对角线互相垂直的平行四边形是菱形.有四条边相等的四边形是菱形.如图, ABCD的两条对角线AC、BD相交于点O,AB= 5 ,AC=8,DB=6
求证:四边形ABCD是菱形.∴四边形ABCD是菱形.∴OA=OC=4
OB=OD=3证明:∵ AB=5 ∴AC⊥BD∴ ∠AOB=(1)∵ 四边形ABCD是平行四边形(平行四边形的对角线互相平分)(对角线互相垂直的平行四边形是菱形). 判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.√ ╳ ╳ ╳ □ABCD的对角线AC与BD相交于点O, (1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。菱矩矩菱请你动脑筋把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?ACDB思考:例题解析:已知: ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F 求证:四边形AFCE是菱形。分析: (1)利用定义判定
(2) 由已知可知
OA=OC,EF⊥AC.
(3)利用四边相等,你会吗? 分析:四边形AFCE是菱形AE=EC=CF=FAAE=ECAF=CFAE=AFEF 垂直平分AC∠1= ∠2∠1= ∠3∠2= ∠3AE∥FC四边形ABCD 是平行四边形AF=CF EF ⊥AC123 二.已知:如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD,PD、PC相交于点P。
(1)猜想:四边形PCOD是什么特殊的四边形? (2)试证明你的猜想。 (3)? PO与CD有怎样的关系?
四边形PCOD是菱形。PO与CD互相垂直且平分如图4-48,CD为Rt△ABC斜边AB上的高,∠BAC的平分线交CD于E,交BC于F,FG⊥AB于G.求证:四边形EGFC为菱形.
一组邻边相等对角线互相垂直四条边相等五种判定方法四边形小结:菱形的判定方法: 作 业5、6四边形1、26矩形与菱形有一角是直角的平行四边形叫做矩形.有一组邻边相等的平行四边形叫做菱形.平行四边形的性质性质边角对角线四个角都是直角相等互相垂直且平分每一组对角判定有一角是直角的平行四边形对角线相等的平行四边形三个角都是直角的四边形有一组邻边相等的平行四边形对角线互相垂直的平行四边形四条边都相等的四边形四条边都相等如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,
证明:CE⊥DF.例:如图,Rt△ABC中,∠ACB=900,∠BAC=600,DE垂直平分BC,垂足为D,交AB于E,又点F在DE的延长线上,且AF=CE,求证:四边形ACEF是菱形。例:如下图在△ABC中,∠BAC=90°,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于C,EF⊥BC于F,四边形AEFG是菱形吗?如图,AD∥BC,BD垂直平分AC,四边形ABCD一定是菱形吗?若是,请说明理由。思考题:┐) 12 (提示: △AOD≌△COB(角边角)AD=BC
如图,已知AD平分∠BAC,DE//AC,
DF//AB,AE=5.
(1)判断四边形AEDF的形状?
(2)它的周长为多少?
练习:如图在菱形ABCD中,CE⊥AB,CF⊥AD.
则CE与CF相等吗?说明理由。
BE与DF呢?已知,如图, ∠ ABC中, ∠ ACB= 900,BF平分∠ ABC,CD垂直于AB于D,和BF交于点G , GE ∥ CA.
求证:CE和FG互相垂直平分。
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
