湘教版数学八年级下册(新) 习题课课件:2.6.1 菱形的性质(共14张PPT)
文档属性
| 名称 | 湘教版数学八年级下册(新) 习题课课件:2.6.1 菱形的性质(共14张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 123.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-14 00:00:00 | ||
图片预览


文档简介
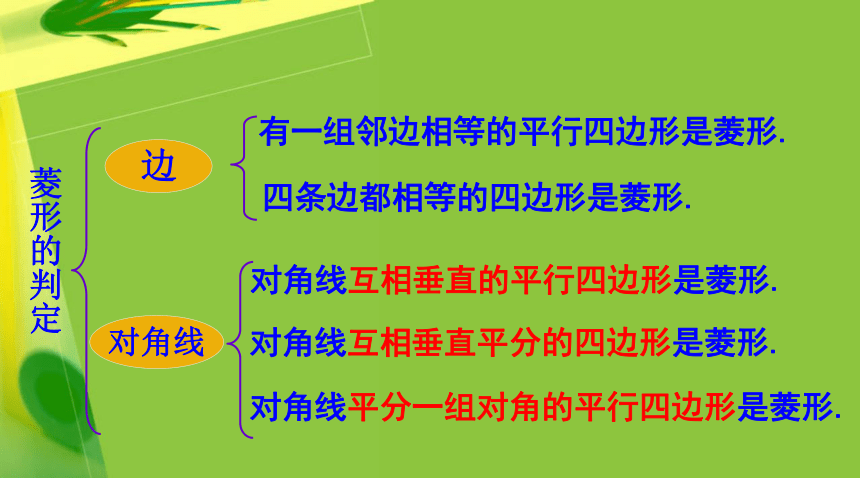
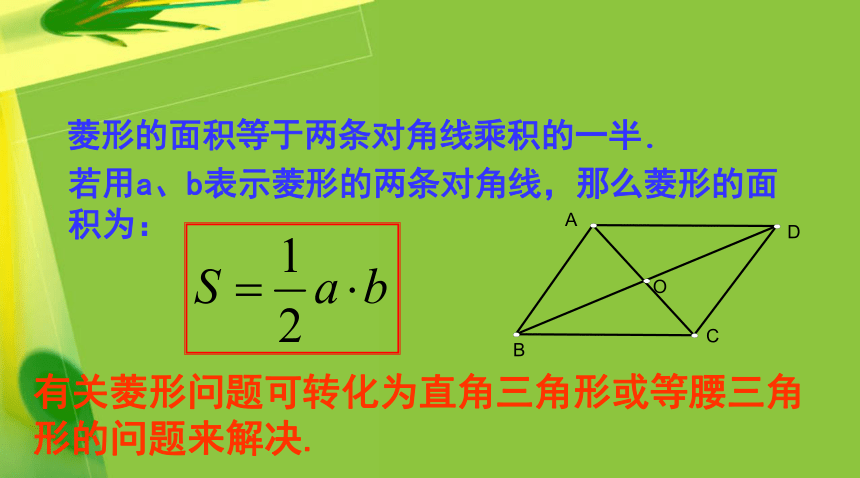
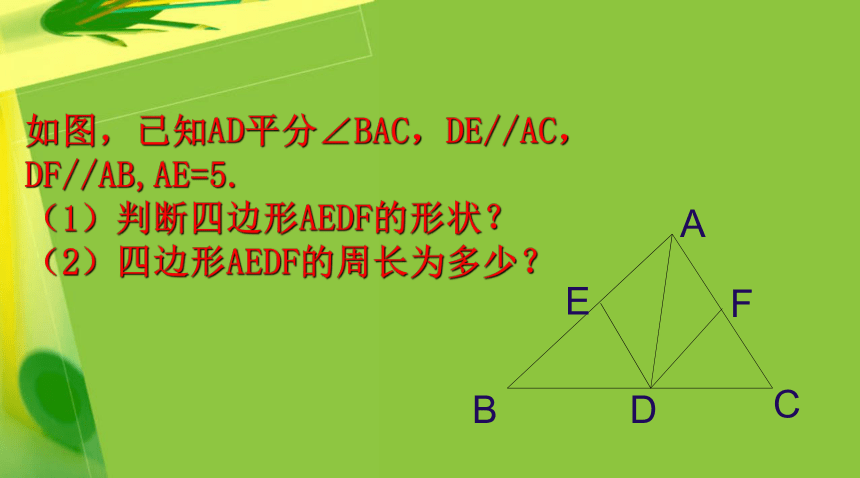
课件14张PPT。菱形的定义一组邻边相等的平行四边形叫做菱形.ABCD菱形的性质边对角线角菱形的性质菱形的两组对边分别平行.菱形的四条边相等.菱形的两组对角分别相等,邻角互补.菱形的两条对角线互相垂直平分.菱形的每一条对角线都平分一组对角.对称性菱形是轴对称图形.观察以下推理,说出语言叙述:∵ 在□ABCD中,AB =AD,∴ □ABCD是菱形.∴四边形ABCD是菱形.∵在四边形ABCD中,AB=BC=CD=DA,∵四边形ABCD是平行四边形,AC ⊥ BD,∴ □ABCD是菱形.有一组邻边相等的平行四边形是菱形.对角线互相垂直的平行四边形是菱形.对角线互相垂直平分的四边形是菱形.四条边都相等的四边形是菱形.边对角线菱形的判定对角线平分一组对角的平行四边形是菱形.菱形的面积等于两条对角线乘积的一半.若用a、b表示菱形的两条对角线,那么菱形的面积为:有关菱形问题可转化为直角三角形或等腰三角形的问题来解决.如图,已知AD平分∠BAC,DE//AC,
DF//AB,AE=5.
(1)判断四边形AEDF的形状?
(2)四边形AEDF的周长为多少?如图,CD为Rt△ABC斜边AB上的高,∠BAC的平分线交CD于E,交BC于F,FG⊥AB于G.
求证:四边形EGFC为菱形.∵ ∠3= 90°-∠1, ∠4= 90°-∠2,∴ CE=CF(等腰三角形的定义)∴ ∠3= ∠4∵ AF是∠BAC的平分线,(角平分线的定义)∴ ∠1= ∠2∵ FC⊥AC, FG⊥AB, AF是∠BAC的平分线,∵ FG⊥AB, CD⊥AB,∴ CD∥FG(垂直于同一条直线的两条直线平行)证明:∴ EC=FG(等量代换)∴四边形CEGF是平行四边形.又∵ FC=FG∴四边形CEGF是菱形.(有一组邻边相等的平行四边形是菱形)如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,CE与AD交与点M, DF与CB交与点N,且AE=AB=BF,
求证:CE⊥DF.
DF//AB,AE=5.
(1)判断四边形AEDF的形状?
(2)四边形AEDF的周长为多少?如图,CD为Rt△ABC斜边AB上的高,∠BAC的平分线交CD于E,交BC于F,FG⊥AB于G.
求证:四边形EGFC为菱形.∵ ∠3= 90°-∠1, ∠4= 90°-∠2,∴ CE=CF(等腰三角形的定义)∴ ∠3= ∠4∵ AF是∠BAC的平分线,(角平分线的定义)∴ ∠1= ∠2∵ FC⊥AC, FG⊥AB, AF是∠BAC的平分线,∵ FG⊥AB, CD⊥AB,∴ CD∥FG(垂直于同一条直线的两条直线平行)证明:∴ EC=FG(等量代换)∴四边形CEGF是平行四边形.又∵ FC=FG∴四边形CEGF是菱形.(有一组邻边相等的平行四边形是菱形)如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,CE与AD交与点M, DF与CB交与点N,且AE=AB=BF,
求证:CE⊥DF.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
