浙江省2024年九年级上册第1次月考模拟考试卷 含解析
文档属性
| 名称 | 浙江省2024年九年级上册第1次月考模拟考试卷 含解析 |  | |
| 格式 | doc | ||
| 文件大小 | 926.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-06 11:32:56 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙江省2024年九年级上册第1次月考模拟考试卷
满分:120分 范围:第1-3章
一.选择题(共10小题,满分30分,每小题3分)
1.下列函数关系中,y是x的二次函数的是( )
A.y=50+x2 B.
C.y=3x+4 D.y=(x+2)(x﹣3)﹣x2
2.下列事件中属于必然事件的是( )
A.一个奇数与一个偶数的和为奇数
B.一个三角形三个内角的和小于180°
C.任意抛一枚均匀的硬币,正面朝上
D.有一匹马奔跑的速度是70米/秒
3.已知⊙O的半径为8cm,点P在⊙O上,则OP的长为( )
A.2cm B.4cm C.8cm D.16cm
4.如图四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转72°后,能与原图形完全重合的是( )
A. B.
C. D.
5.下列命题中,正确的是( )
A.任意三点确定一个圆
B.平分弦的直径垂直于弦
C.圆既是轴对称图形又是中心对称图形
D.垂直弦的直线必过圆心
6.对于y=﹣2(x﹣3)2+2的图象下列叙述正确的是( )
A.顶点坐标为(﹣3,2) B.对称轴为:直线x=﹣3
C.当x≥3时y随x增大而减小 D.函数的最小值是2
7.某校计划组织研学活动,现有四个地点可供选择:毛店、森山小镇、八都水库、德胜岩,若从中随机选择一个地点,则选中“八都水库”或“毛店”的概率为( )
A. B. C. D.
8.已知k是不为0的常数,则函数y=kx与y=kx2+k2的图象可能是( )
A. B. C. D.
9.如图,D是等边△ABC外接圆上的点,且∠DAC=20°,则∠ACD的度数为( )
A.20° B.30° C.40° D.45°
10.二位同学在研究函数y=a(x+3)(x﹣)(a为实数,且a≠0)时,甲发现当0<a<1时,函数图象的顶点在第四象限;乙发现方程a(x+3)(x﹣)+5=0必有两个不相等的实数根.则( )
A.甲、乙的结论都错误
B.甲的结论正确,乙的结论错误
C.甲、乙的结论都正确
D.甲的结论错误,乙的结论正确
二.填空题(共6小题,满分24分,每小题4分)
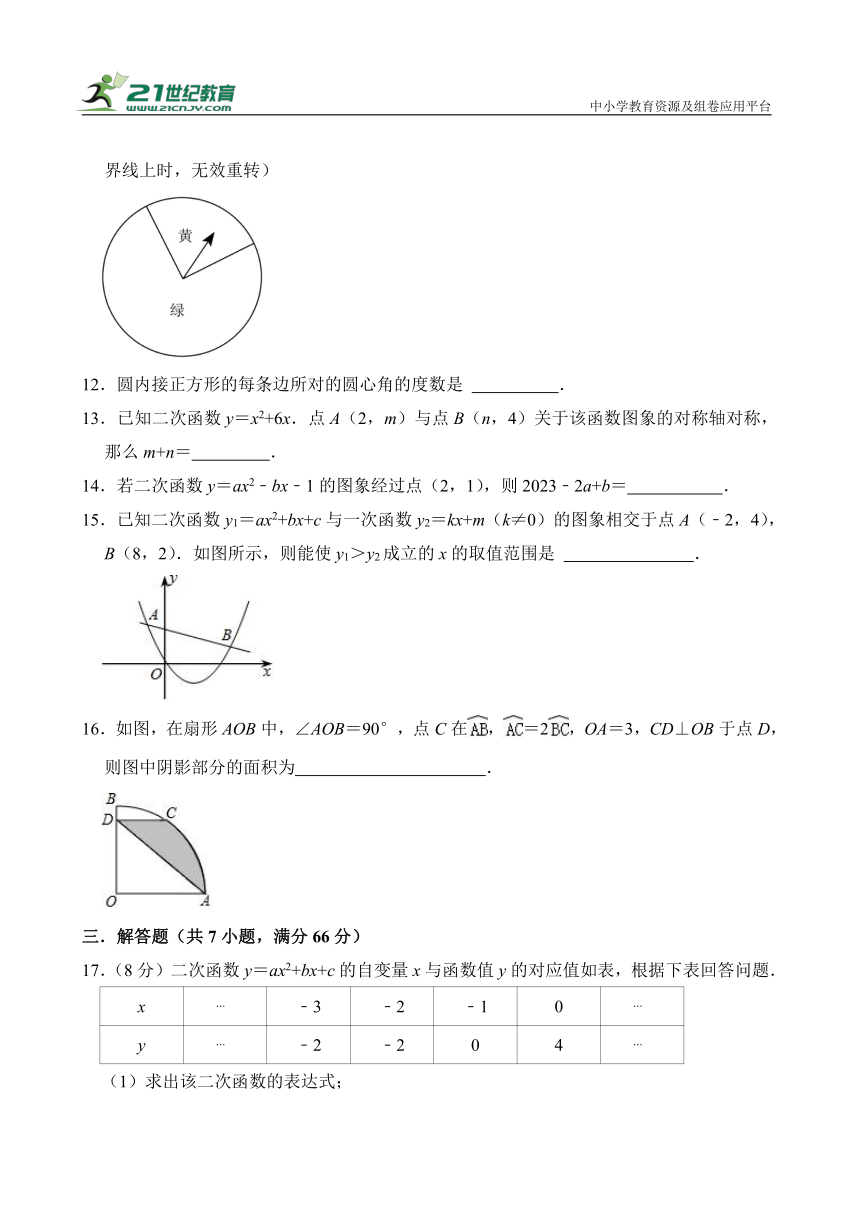
11.如图,转盘中黄色扇形的圆心角为90°,绿色扇形的圆心角为270°,现让转盘自由转动两次,则两次指针都落在绿色区域的概率为 .(注:当指针恰好指在分界线上时,无效重转)
12.圆内接正方形的每条边所对的圆心角的度数是 .
13.已知二次函数y=x2+6x.点A(2,m)与点B(n,4)关于该函数图象的对称轴对称,那么m+n= .
14.若二次函数y=ax2﹣bx﹣1的图象经过点(2,1),则2023﹣2a+b= .
15.已知二次函数y1=ax2+bx+c与一次函数y2=kx+m(k≠0)的图象相交于点A(﹣2,4),B(8,2).如图所示,则能使y1>y2成立的x的取值范围是 .
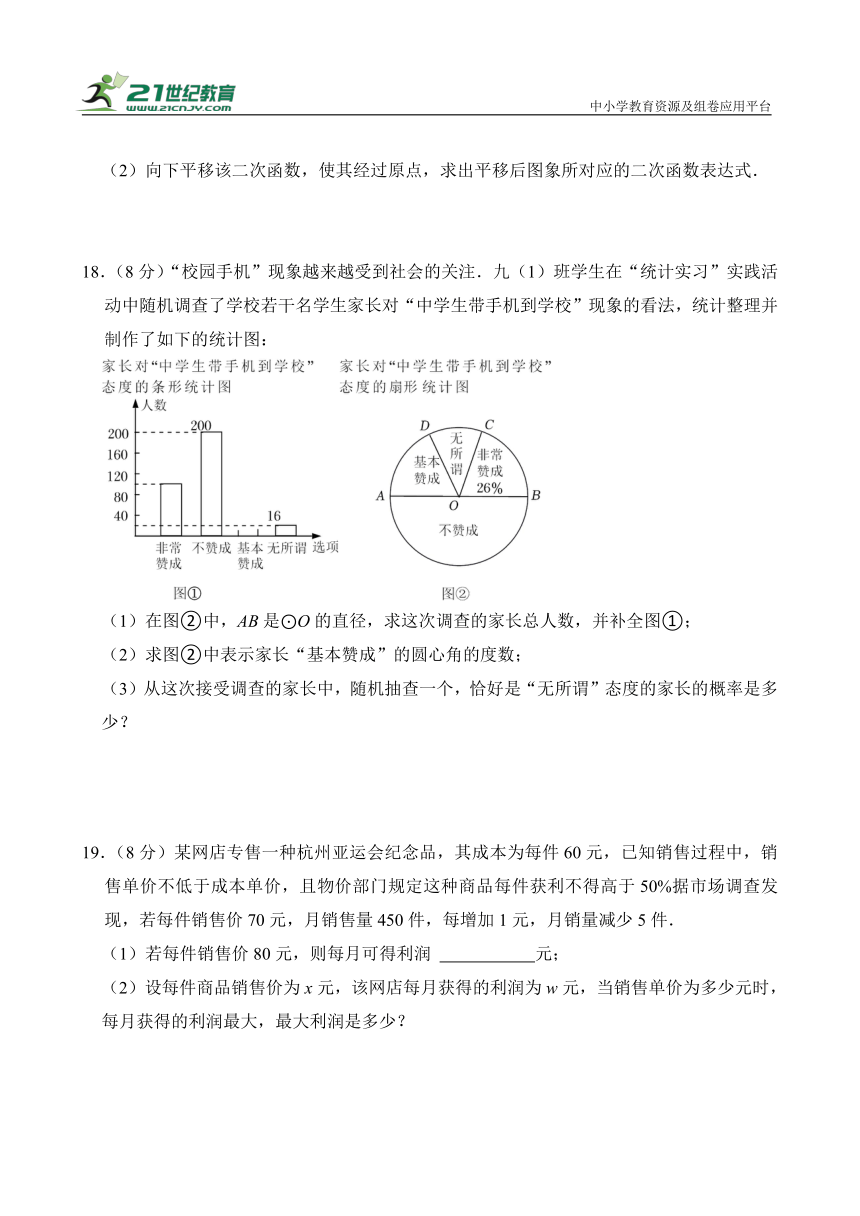
16.如图,在扇形AOB中,∠AOB=90°,点C在,=2,OA=3,CD⊥OB于点D,则图中阴影部分的面积为 .
三.解答题(共7小题,满分66分)
17.(8分)二次函数y=ax2+bx+c的自变量x与函数值y的对应值如表,根据下表回答问题.
x ﹣3 ﹣2 ﹣1 0
y ﹣2 ﹣2 0 4
(1)求出该二次函数的表达式;
(2)向下平移该二次函数,使其经过原点,求出平移后图象所对应的二次函数表达式.
18.(8分)“校园手机”现象越来越受到社会的关注.九(1)班学生在“统计实习”实践活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图:
(1)在图②中,AB是⊙O的直径,求这次调查的家长总人数,并补全图①;
(2)求图②中表示家长“基本赞成”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“无所谓”态度的家长的概率是多少?
19.(8分)某网店专售一种杭州亚运会纪念品,其成本为每件60元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品每件获利不得高于50%据市场调查发现,若每件销售价70元,月销售量450件,每增加1元,月销量减少5件.
(1)若每件销售价80元,则每月可得利润 元;
(2)设每件商品销售价为x元,该网店每月获得的利润为w元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
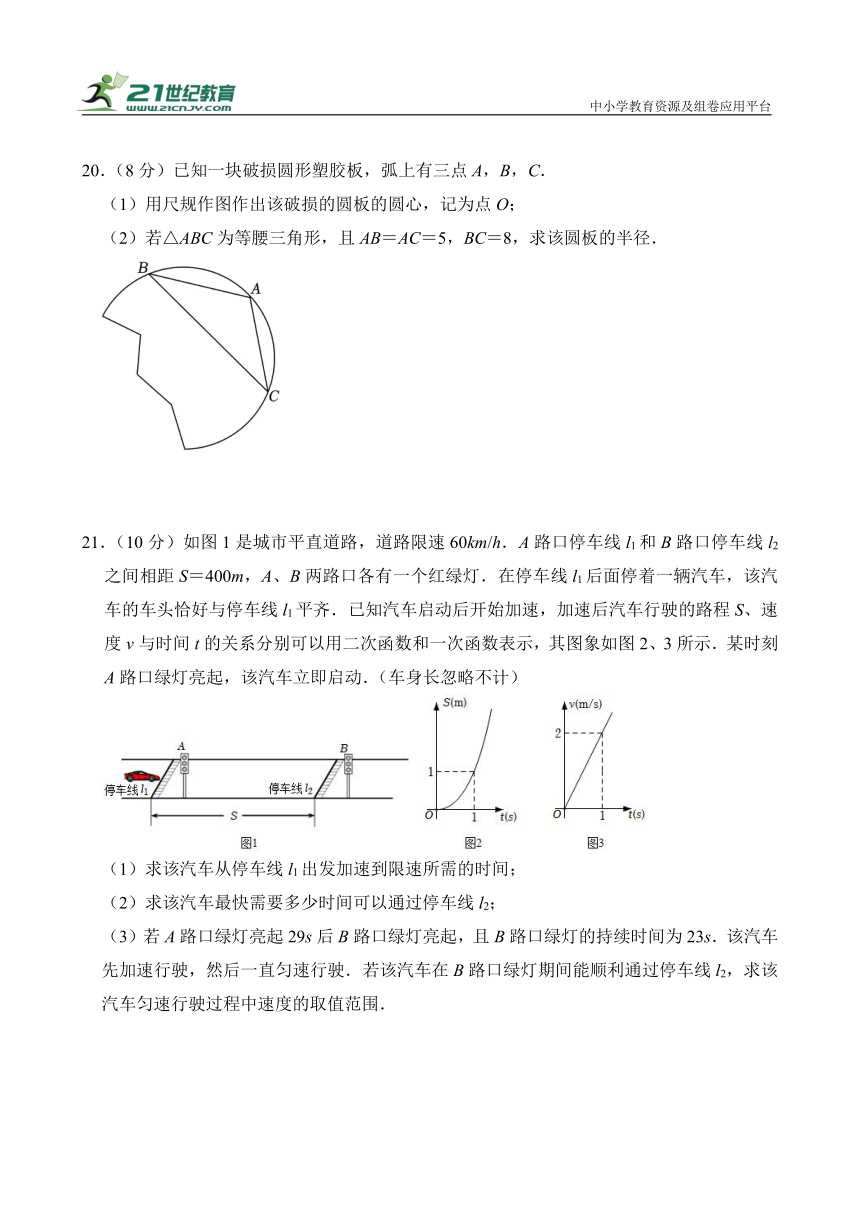
20.(8分)已知一块破损圆形塑胶板,弧上有三点A,B,C.
(1)用尺规作图作出该破损的圆板的圆心,记为点O;
(2)若△ABC为等腰三角形,且AB=AC=5,BC=8,求该圆板的半径.
21.(10分)如图1是城市平直道路,道路限速60km/h.A路口停车线l1和B路口停车线l2之间相距S=400m,A、B两路口各有一个红绿灯.在停车线l1后面停着一辆汽车,该汽车的车头恰好与停车线l1平齐.已知汽车启动后开始加速,加速后汽车行驶的路程S、速度v与时间t的关系分别可以用二次函数和一次函数表示,其图象如图2、3所示.某时刻A路口绿灯亮起,该汽车立即启动.(车身长忽略不计)
(1)求该汽车从停车线l1出发加速到限速所需的时间;
(2)求该汽车最快需要多少时间可以通过停车线l2;
(3)若A路口绿灯亮起29s后B路口绿灯亮起,且B路口绿灯的持续时间为23s.该汽车先加速行驶,然后一直匀速行驶.若该汽车在B路口绿灯期间能顺利通过停车线l2,求该汽车匀速行驶过程中速度的取值范围.
22.(12分)有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
(1)如图1,在半对角四边形ABCD中,,,求出∠B与∠C的度数之和;
(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO.∠OBA的平分线交OA于点E,连接DE并延长交AC于点F,若∠AFE=2∠EAF.求证:四边形DBCF是半对角四边形.
23.(12分)如图,二次函数y=(t﹣1)x2+(t+1)x+2(t≠1),x=0与x=3时的函数值相等,其图象与x轴交于A、B两点,与y轴正半轴交于C点.
(1)求二次函数的解析式.
(2)在第一象限的抛物线上求点P,使得S△PBC最大.
(3)点P是抛物线上x轴上方一点,若∠CAP=45°,求P点坐标.
浙江省2024年九年级上册第1次月考模拟考试卷
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.下列函数关系中,y是x的二次函数的是( )
A.y=50+x2 B.
C.y=3x+4 D.y=(x+2)(x﹣3)﹣x2
【分析】根据二次函数的定义:形如y=ax2+bx+c(a≠0),这样的函数叫做二次函数,进行判断即可.
【解答】解:A、y=50+x2是二次函数,符合题意;
B、,含有分式,不是二次函数,不符合题意;
C、y=3x+4,是一次函数,不符合题意;
D、y=(x+2)(x﹣3)﹣x2=﹣x﹣6,是一次函数,不符合题意;
故选:A.
2.下列事件中属于必然事件的是( )
A.一个奇数与一个偶数的和为奇数
B.一个三角形三个内角的和小于180°
C.任意抛一枚均匀的硬币,正面朝上
D.有一匹马奔跑的速度是70米/秒
【分析】根据事件发生的可能性大小判断即可.
【解答】解:A、一个奇数与一个偶数的和为奇数,是必然事件,符合题意;
B、一个三角形三个内角的和小于180°,是不可能事件,不符合题意;
C、任意抛一枚均匀的硬币,正面朝上,是随机事件,不符合题意;
D、有一匹马奔跑的速度是70米/秒,是不可能事件,不符合题意;
故选:A.
3.已知⊙O的半径为8cm,点P在⊙O上,则OP的长为( )
A.2cm B.4cm C.8cm D.16cm
【分析】根据点在圆上,点到圆心的距离等于圆的半径求解.
【解答】解:∵点P在⊙O上,
∴OP=8cm.
故选:C.
4.如图四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转72°后,能与原图形完全重合的是( )
A. B.
C. D.
【分析】观察图形,从图形的性质可以确定旋转角,然后进行判断即可得到答案.
【解答】解:A图形顺时针旋转120°后,能与原图形完全重合,A不正确;
B图形顺时针旋转90°后,能与原图形完全重合,B不正确;
C图形顺时针旋转180°后,能与原图形完全重合,C不正确;
D图形顺时针旋转72°后,能与原图形完全重合,D正确,
故选:D.
5.下列命题中,正确的是( )
A.任意三点确定一个圆
B.平分弦的直径垂直于弦
C.圆既是轴对称图形又是中心对称图形
D.垂直弦的直线必过圆心
【分析】根据不共线的三点确定一个圆、垂径定理的推论和圆的有关性质分别判断.
【解答】解:不共线的三点确定一个圆,所以A选项不正确;
平分(非直径)弦的直径垂直于弦,所以B选项不正确;
圆既是轴对称图形又是中心对称图形,过圆心的直线都是它的对称轴,圆心是它的对称中心,所以C选项正确;
弦的垂直平分线必过圆心,所以D选项不正确;
故选:C.
6.对于y=﹣2(x﹣3)2+2的图象下列叙述正确的是( )
A.顶点坐标为(﹣3,2)
B.对称轴为:直线x=﹣3
C.当x≥3时y随x增大而减小
D.函数的最小值是2
【分析】由抛物线解析式可求得其顶点坐标、对称轴、开口方向,进一步可求得其最值及增减性.
【解答】解:
∵y=﹣2(x﹣3)2+2,
∴抛物线开口向下,顶点坐标为(3,2),对称轴为x=3,当x=3时,函数有最大值2,
∴A、B、D不正确;
∵对称轴为x=3,且开口向下,
∴当x≥3时y随x的增大而减小,
故选:C.
7.某校计划组织研学活动,现有四个地点可供选择:毛店、森山小镇、八都水库、德胜岩,若从中随机选择一个地点,则选中“八都水库”或“毛店”的概率为( )
A. B. C. D.
【分析】根据概率公式可直接求解.
【解答】解:∵有四个地点可供选择:毛店、森山小镇、八都水库、德胜岩,
∴若从中随机选择一个地点,则选中“八都水库”或“毛店”的概率为;
故选:C.
8.已知k是不为0的常数,则函数y=kx与y=kx2+k2的图象可能是( )
A. B.
C. D.
【分析】分两种情况进行讨论:k>0与k<0进行讨论即可.
【解答】解:当k>0时,抛物线y=kx2+k2开口向上,与y轴正半轴相交,函数y=kx经过第一、三象限,选项中没有符合的;
当k<0时,抛物线y=kx2+k2开口向下,与y轴正半轴相交,函数y=kx经过第二、四象限,故A选项符合题意;
故选:A.
9.如图,D是等边△ABC外接圆上的点,且∠DAC=20°,则∠ACD的度数为( )
A.20° B.30° C.40° D.45°
【分析】根据圆内接四边形的性质得到∠D=180°﹣∠B=120°,根据三角形内角和定理计算即可.
【解答】解:∵△ABC是等边三角形,
∴∠B=60°,
∵四边形ABCD是圆内接四边形,
∴∠D=180°﹣∠B=120°,
∴∠ACD=180°﹣∠DAC﹣∠D=40°,
故选:C.
10.二位同学在研究函数y=a(x+3)(x﹣)(a为实数,且a≠0)时,甲发现当0<a<1时,函数图象的顶点在第四象限;乙发现方程a(x+3)(x﹣)+5=0必有两个不相等的实数根.则( )
A.甲、乙的结论都错误
B.甲的结论正确,乙的结论错误
C.甲、乙的结论都正确
D.甲的结论错误,乙的结论正确
【分析】由函数解析式确定函数与x轴的两个交点的横坐标分别是﹣3和,再由函数的对称性确定函数顶点的横坐标为,根据甲的说法求0<a<1时的范围,即可确定甲的说法错误;将方程a(x+3)(x﹣)+5=0化为一元二次方程ax2+(3a﹣2)x﹣1=0,求判别式Δ=9(a﹣)2+>0,即可确定方程的根的情况.
【解答】解:由函数y=a(x+3)(x﹣)可知,函数与x轴的两个交点的横坐标分别是﹣3和,
∴函数顶点的横坐标为,
∵0<a<1,
∴>﹣,
∴函数的顶点不一定在第四象限,故甲的结论错误;
∵a(x+3)(x﹣)+5=0可以化为ax2+(3a﹣2)x﹣1=0,
Δ=(3a﹣2)2+4a=9a2﹣8a+4=9(a﹣)2+>0,
∴a(x+3)(x﹣)+5=0必有两个不相等的实数根,
故乙的结论正确;
故选:D.
二.填空题(共6小题,满分24分,每小题4分)
11.如图,转盘中黄色扇形的圆心角为90°,绿色扇形的圆心角为270°,现让转盘自由转动两次,则两次指针都落在绿色区域的概率为 .(注:当指针恰好指在分界线上时,无效重转)
【分析】通过计算转盘的黄色扇形和绿色扇形的面积之比可得到2次指针都落在绿色区域的概率.
【解答】解:由图得:黄色扇形的圆心角为90°,绿色扇形的圆心角是270°,
∴黄色扇形的面积:绿色扇形的面积=,
如图,
故让转盘自由转动2次,2次指针都落在绿色区域的概率是.
故答案为:.
12.圆内接正方形的每条边所对的圆心角的度数是 90° .
【分析】根据圆内接正方形的中心角的概念计算即可.
【解答】解:圆内接正方形的一条边所对的圆心角的度数为:,
故答案为:90°.
13.已知二次函数y=x2+6x.点A(2,m)与点B(n,4)关于该函数图象的对称轴对称,那么m+n= ﹣4 .
【分析】首先求出抛物线y=x2+6x的对称轴,然后根据点A(2,m)与点B(n,4)关于该抛物线的对称轴对称,即可求出m+n的值.
【解答】解:∵抛物线解析式为y=x2+6x,
∴抛物线的对称轴x=﹣3,
∵点A(2,m)与点B(n,4)关于该抛物线的对称轴对称,
∴2+n=﹣6,m=4,
解得n=﹣8,
故m+n=4﹣8=﹣4,
故答案为:﹣4.
14.若二次函数y=ax2﹣bx﹣1的图象经过点(2,1),则2023﹣2a+b= 2022 .
【分析】把点(2,1)代入函数解析式求出2a﹣b=1,然后即可得解.
【解答】解:∵y=ax2﹣bx﹣1的图象经过点(2,1),
∴4a﹣2b﹣1=1,
∴2a﹣b=1,
∴2023﹣2a+b=2023﹣(2a﹣b)=2023﹣1=2022,
故答案为:2022.
15.已知二次函数y1=ax2+bx+c与一次函数y2=kx+m(k≠0)的图象相交于点A(﹣2,4),B(8,2).如图所示,则能使y1>y2成立的x的取值范围是 x<﹣2或x>8 .
【分析】直接根据函数的图象即可得出结论.
【解答】解:∵由函数图象可知,当x<﹣2或x>8时,一次函数的图象在二次函数的下方,
∴能使y1>y2成立的x的取值范围是x<﹣2或x>8.
故答案为:x<﹣2或x>8.
16.如图,在扇形AOB中,∠AOB=90°,点C在,=2,OA=3,CD⊥OB于点D,则图中阴影部分的面积为 π﹣ .
【分析】连接OC,AC,由点C为的三等分点,∠AOB=90°,得到∠COD=30°,∠AOC=60°,根据CD⊥OB,得到S△OCD=S△ACD,根据扇形和三角形的面积公式即可得到结论.
【解答】解:连接OC,AC,
∵点C为
的三等分点,∠AOB=90°,
∴∠COD=30°,∠AOC=60°,
∵CD⊥OB,
∴S△OCD=S△ACD,
∵∠CDO=90°,∠DOC=30°,OC=OA=3,
∴CD=,OD=,
∴图中阴影部分的面积=S△ACD+S弓形AC=+××+﹣×3×=﹣,
故答案为:π﹣.
三.解答题(共7小题,满分66分)
17.(8分)二次函数y=ax2+bx+c的自变量x与函数值y的对应值如表,根据下表回答问题.
x ﹣3 ﹣2 ﹣1 0
y ﹣2 ﹣2 0 4
(1)求出该二次函数的表达式;
(2)向下平移该二次函数,使其经过原点,求出平移后图象所对应的二次函数表达式.
【分析】(1)把(﹣2,﹣2),(﹣1,0),(0,4)代入二次函数y=ax2+bx+c,即可求出a、b、c的值,进而得出函数的解析式;
(2)结合(1)中求得的抛物线解析式即可得到平移后图象所对应的二次函数的表达式.
【解答】解:(1)∵(﹣2,﹣2),(﹣1,0),(0,4))均在抛物线y=ax2+bx+c上,
∴,
解得,
∴抛物线的解析式为:y=x2+5x+4;
(2)∵抛物线向下平移4个单位后经过原点.
∴平移后图象所对应的二次函数的表达式是y=x2+5x.
18.(8分)“校园手机”现象越来越受到社会的关注.九(1)班学生在“统计实习”实践活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图:
(1)在图②中,AB是⊙O的直径,求这次调查的家长总人数,并补全图①;
(2)求图②中表示家长“基本赞成”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“无所谓”态度的家长的概率是多少?
【分析】(1)根据两个统计图可知,“不赞成”的有200人,占调查人数的50%,可求出调查人数,再求出“基本赞成”的人数,补全统计图;
(2)求出“基本赞成”所占的百分比,进而求出相应圆心角的度数;
(3)根据概率的定义进行计算即可.
【解答】解:(1)由于AB是⊙O的直径,所以“不赞成”占调查总人数的50%,
200÷50%=400(人),
样本中“非常赞成”的人数:400×26%=104(人),
“基本赞成”的人数为:400﹣200﹣104﹣16=80(人),
补全的统计图如下:
(2)360°×=72°,
答:图②中表示家长“基本赞成”的圆心角的度数为72°;
(3)样本中,被调查的400名家长中,“无所谓”的有16名,
所以随机抽查一个,恰好是“无所谓”态度的家长的概率是=,
答:随机抽查一个,恰好是“无所谓”态度的家长的概率是.
19.(8分)某网店专售一种杭州亚运会纪念品,其成本为每件60元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品每件获利不得高于50%据市场调查发现,若每件销售价70元,月销售量450件,每增加1元,月销量减少5件.
(1)若每件销售价80元,则每月可得利润 8000 元;
(2)设每件商品销售价为x元,该网店每月获得的利润为w元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
【分析】(1)根据利润=每件利润×月销售量即可得出答案;
(2)设每件商品销售价为x元,则每件的利润为(x﹣60)元,销售量为450﹣5×(x﹣70)=800﹣5x(件),根据“月利润=每件利润×月销售量”列出函数解析式,配方成顶点式后依据二次函数的性质求解即可得出答案.
【解答】解:(1)若每件销售价80元,则每月可得利润(80﹣60)×(450﹣5×10)=8000(元),
故答案为:8000;
(2)设每件商品销售价为x元,
则每件的利润为(x﹣60)元,销售量为450﹣5×(x﹣70)=800﹣5x(件),
所以该网店每月获得的利润为w=(x﹣60)(800﹣5x)
=﹣5x2+1100x﹣48000
=﹣5(x﹣110)2+12500,
∵每件获利不得高于50%,
∴x≤60×(1+50%)=90,
∵﹣5<0,
∴当x<110时,w随x的增大而增大,
∴当x=90时,w取得最大值,最大值为10500元.
答:当销售单价为90元时,每月获得的利润最大,最大利润是10500元.
20.(8分)已知一块破损圆形塑胶板,弧上有三点A,B,C.
(1)用尺规作图作出该破损的圆板的圆心,记为点O;
(2)若△ABC为等腰三角形,且AB=AC=5,BC=8,求该圆板的半径.
【分析】(1)作BC、AB的垂直平分线,它们的交点即为圆心O;
(2)连接OA、OB,OA交BC于D点,如图,先利用AB=AC得到=,则根据垂径定理得到∠ADB=∠ODB=90°,BD=CD=BC=4,再利用勾股定理计算出AD=3,设⊙O的半径为r,则OB=r,OD=r﹣3,在Rt△BOD中利用勾股定理得到42+(r﹣3)2=r2,然后解方程即可.
【解答】解:(1)如图,点O为所作;
(2)连接OA、OB,OA交BC于D点,如图,
∵AB=AC,
∴=,
∴OA垂直平分BC,
∴∠ADB=∠ODB=90°,BD=CD=BC=4,
在Rt△ABD中,∵AB=5,BD=4,
∴AD==3,
设⊙O的半径为r,则OB=r,OD=r﹣3,
在Rt△BOD中,42+(r﹣3)2=r2,
解得r=,
即该圆板的半径为.
21.(10分)如图1是城市平直道路,道路限速60km/h.A路口停车线l1和B路口停车线l2之间相距S=400m,A、B两路口各有一个红绿灯.在停车线l1后面停着一辆汽车,该汽车的车头恰好与停车线l1平齐.已知汽车启动后开始加速,加速后汽车行驶的路程S、速度v与时间t的关系分别可以用二次函数和一次函数表示,其图象如图2、3所示.某时刻A路口绿灯亮起,该汽车立即启动.(车身长忽略不计)
(1)求该汽车从停车线l1出发加速到限速所需的时间;
(2)求该汽车最快需要多少时间可以通过停车线l2;
(3)若A路口绿灯亮起29s后B路口绿灯亮起,且B路口绿灯的持续时间为23s.该汽车先加速行驶,然后一直匀速行驶.若该汽车在B路口绿灯期间能顺利通过停车线l2,求该汽车匀速行驶过程中速度的取值范围.
【分析】(1)先将限速单位化为m/s,根据图3求得v=2t,代入求解即可;
(2)根据(1)的结论求得加速时间,根据题意求得运算时间,分别求得两段时间内的路程,进而即可求得答案;
(3)设该汽车匀速行驶过程中的速度为v m/s,根据题意根据(2)的方法求得两段路程所用时间,结合题意中绿灯等亮起期间所用时间,分别列出方程,即可该汽车匀速行驶过程中速度的取值范围.
【解答】解:∵限速为60km/h=m/s,
由图3可知,当t=1时,v=2,
设v=kt,解得k=2,
∴v=2t,
∴t==×=s.
(2)由图2可知,当t=1时,S=1,且x=0时,S=0,
设S=at2,
∴1=a×12,
解得a=1,
∴S=t2(t≥0),
由(1)可知汽车从停车线l1出发加速到限速所需的时间s.
则S=()2=m,
以m/s行驶时间为:=s,
∴+==28s,
∴该汽车最快需要28s可以通过停车线l2;
(3)设该汽车匀速行驶过程中的速度为v m/s,即求出加速到v,
由(1)可得汽车加速到v所用的时间为t=,
则汽车从停车线l1出发加速到v m/s的路程为S=()2,匀速所用的时间为s,
根据题意可得当B路口绿灯亮起时通过,则+=29,
解得v=16或v=100(舍),经检验v=16是原方程的解,
可得当B路口绿灯熄灭时候通过,则+=29+23,
解得v=8或v=200(舍),经检验v=8是原方程的解,
综上所述,该汽车匀速行驶过程中的速度v的范围为8≤v≤16.
22.(12分)有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
(1)如图1,在半对角四边形ABCD中,,,求出∠B与∠C的度数之和;
(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO.∠OBA的平分线交OA于点E,连接DE并延长交AC于点F,若∠AFE=2∠EAF.求证:四边形DBCF是半对角四边形.
【分析】(1)根据半对角四边形的定义和四边形的内角和为360°求解即可;
(2)证明△BDE≌△BOE得出∠BDE=∠BOE,进而可证得∠BDE=2∠C,连接OC,设∠OAC=∠OCA=x,可得∠AFE=2x,∠DFC=180°﹣2x,∠AOC=180°﹣2x=2∠ABC,即可证得结论;
【解答】(1)解:∵在半对角四边形ABCD中,∠B=∠D,∠C=∠A,
∴∠D=2∠B,∠A=2∠C,
∵∠A+2B+∠C+D=360°,
∴3∠B+3∠C=360°,
∴∠B+∠C=120°.
(2)证明:∵BE是∠OBA的平分线,
∴∠DBE=∠OBE,
∵DE=OE,BE=BE,
∴△BDE≌△BOE (SSS),
∴∠BDE=∠BOE,
又∵∠ACB=∠BOA,
∴∠ACB=BDE,
连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
设∠OAC=∠OCA=x,
∵∠AFE=2∠EAF,
∴∠AFE=2x,
∴∠DFC=180°﹣2x,
∵∠AOC=180°﹣2x=2∠ABC,
∴∠DFC=2∠ABC,
∴∠ABC=∠DFC,
∴四边形BCFD是半对角四边形.
23.(12分)如图,二次函数y=(t﹣1)x2+(t+1)x+2(t≠1),x=0与x=3时的函数值相等,其图象与x轴交于A、B两点,与y轴正半轴交于C点.
(1)求二次函数的解析式.
(2)在第一象限的抛物线上求点P,使得S△PBC最大.
(3)点P是抛物线上x轴上方一点,若∠CAP=45°,求P点坐标.
【分析】分析:(1)由x=0与x=3时的函数值相等,列方程求出t值即可求解;
(2)利用待定系数法先求出直线BC的解析式,然后过点P作y轴的平行线,交直线BC于点D,用未知数设出点P、D的坐标,即可得到线段PD的长度表达式,以PD为底、OB为高,即可得到△PBC的面积函数关系式,根据函数的性质即可求出△PBC的面积最大时,点P的坐标;
(3)如图,将AC绕点A顺时针旋转90°得到AC′,则C′(1,﹣1),取CC′的中点H,作直线AH交抛物线于P,则∠CAP=45°,求出直线AH的解析式,利用方程组即可即可求出点P坐标;
【解答】解:(1)∵x=0与x=3时的函数值相等,
∴(t﹣1)×02+(t+1)×0+2=(t﹣1)×32+(t+1)×3+2,
解方程,得t=,
把t=代入二次函数y=(t﹣1)x2+(t+1)x+2(t≠1),
∴二次函数的解析式为:y=.
(2)如图过点P作PD∥y轴,交BC于点D.
把y=0代入y=,得为:=0,
解,得x1=﹣1,x2=4,
∴点A(﹣1,0),B(4,0),
又∵C(0,2)
∴直线BC:y=x+2,
设点P(a,),
把x=a代入y=x+2,y=﹣a+2,
∴点D的坐标为(a,﹣a+2),
∴PD=﹣(﹣a+2)=,
∴S△PBC==×()×4=﹣a2+4a=﹣(a﹣2)2+4,
当a=2时,S△PBC有最大值,最大值为4,
所以点P的坐标(2,3),
(3)如图,将AC绕点A顺时针旋转90°得到AC′,则C′(1,﹣1),取CC′的中点H,作直线AH交抛物线于P,则∠CAP=45°,
∵A(﹣1,0),H(,),
∴直线AH的解析式为y=x+,
由,解得或,
∴P(,).
浙江省2024年九年级上册第1次月考模拟考试卷
满分:120分 范围:第1-3章
一.选择题(共10小题,满分30分,每小题3分)
1.下列函数关系中,y是x的二次函数的是( )
A.y=50+x2 B.
C.y=3x+4 D.y=(x+2)(x﹣3)﹣x2
2.下列事件中属于必然事件的是( )
A.一个奇数与一个偶数的和为奇数
B.一个三角形三个内角的和小于180°
C.任意抛一枚均匀的硬币,正面朝上
D.有一匹马奔跑的速度是70米/秒
3.已知⊙O的半径为8cm,点P在⊙O上,则OP的长为( )
A.2cm B.4cm C.8cm D.16cm
4.如图四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转72°后,能与原图形完全重合的是( )
A. B.
C. D.
5.下列命题中,正确的是( )
A.任意三点确定一个圆
B.平分弦的直径垂直于弦
C.圆既是轴对称图形又是中心对称图形
D.垂直弦的直线必过圆心
6.对于y=﹣2(x﹣3)2+2的图象下列叙述正确的是( )
A.顶点坐标为(﹣3,2) B.对称轴为:直线x=﹣3
C.当x≥3时y随x增大而减小 D.函数的最小值是2
7.某校计划组织研学活动,现有四个地点可供选择:毛店、森山小镇、八都水库、德胜岩,若从中随机选择一个地点,则选中“八都水库”或“毛店”的概率为( )
A. B. C. D.
8.已知k是不为0的常数,则函数y=kx与y=kx2+k2的图象可能是( )
A. B. C. D.
9.如图,D是等边△ABC外接圆上的点,且∠DAC=20°,则∠ACD的度数为( )
A.20° B.30° C.40° D.45°
10.二位同学在研究函数y=a(x+3)(x﹣)(a为实数,且a≠0)时,甲发现当0<a<1时,函数图象的顶点在第四象限;乙发现方程a(x+3)(x﹣)+5=0必有两个不相等的实数根.则( )
A.甲、乙的结论都错误
B.甲的结论正确,乙的结论错误
C.甲、乙的结论都正确
D.甲的结论错误,乙的结论正确
二.填空题(共6小题,满分24分,每小题4分)
11.如图,转盘中黄色扇形的圆心角为90°,绿色扇形的圆心角为270°,现让转盘自由转动两次,则两次指针都落在绿色区域的概率为 .(注:当指针恰好指在分界线上时,无效重转)
12.圆内接正方形的每条边所对的圆心角的度数是 .
13.已知二次函数y=x2+6x.点A(2,m)与点B(n,4)关于该函数图象的对称轴对称,那么m+n= .
14.若二次函数y=ax2﹣bx﹣1的图象经过点(2,1),则2023﹣2a+b= .
15.已知二次函数y1=ax2+bx+c与一次函数y2=kx+m(k≠0)的图象相交于点A(﹣2,4),B(8,2).如图所示,则能使y1>y2成立的x的取值范围是 .
16.如图,在扇形AOB中,∠AOB=90°,点C在,=2,OA=3,CD⊥OB于点D,则图中阴影部分的面积为 .
三.解答题(共7小题,满分66分)
17.(8分)二次函数y=ax2+bx+c的自变量x与函数值y的对应值如表,根据下表回答问题.
x ﹣3 ﹣2 ﹣1 0
y ﹣2 ﹣2 0 4
(1)求出该二次函数的表达式;
(2)向下平移该二次函数,使其经过原点,求出平移后图象所对应的二次函数表达式.
18.(8分)“校园手机”现象越来越受到社会的关注.九(1)班学生在“统计实习”实践活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图:
(1)在图②中,AB是⊙O的直径,求这次调查的家长总人数,并补全图①;
(2)求图②中表示家长“基本赞成”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“无所谓”态度的家长的概率是多少?
19.(8分)某网店专售一种杭州亚运会纪念品,其成本为每件60元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品每件获利不得高于50%据市场调查发现,若每件销售价70元,月销售量450件,每增加1元,月销量减少5件.
(1)若每件销售价80元,则每月可得利润 元;
(2)设每件商品销售价为x元,该网店每月获得的利润为w元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
20.(8分)已知一块破损圆形塑胶板,弧上有三点A,B,C.
(1)用尺规作图作出该破损的圆板的圆心,记为点O;
(2)若△ABC为等腰三角形,且AB=AC=5,BC=8,求该圆板的半径.
21.(10分)如图1是城市平直道路,道路限速60km/h.A路口停车线l1和B路口停车线l2之间相距S=400m,A、B两路口各有一个红绿灯.在停车线l1后面停着一辆汽车,该汽车的车头恰好与停车线l1平齐.已知汽车启动后开始加速,加速后汽车行驶的路程S、速度v与时间t的关系分别可以用二次函数和一次函数表示,其图象如图2、3所示.某时刻A路口绿灯亮起,该汽车立即启动.(车身长忽略不计)
(1)求该汽车从停车线l1出发加速到限速所需的时间;
(2)求该汽车最快需要多少时间可以通过停车线l2;
(3)若A路口绿灯亮起29s后B路口绿灯亮起,且B路口绿灯的持续时间为23s.该汽车先加速行驶,然后一直匀速行驶.若该汽车在B路口绿灯期间能顺利通过停车线l2,求该汽车匀速行驶过程中速度的取值范围.
22.(12分)有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
(1)如图1,在半对角四边形ABCD中,,,求出∠B与∠C的度数之和;
(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO.∠OBA的平分线交OA于点E,连接DE并延长交AC于点F,若∠AFE=2∠EAF.求证:四边形DBCF是半对角四边形.
23.(12分)如图,二次函数y=(t﹣1)x2+(t+1)x+2(t≠1),x=0与x=3时的函数值相等,其图象与x轴交于A、B两点,与y轴正半轴交于C点.
(1)求二次函数的解析式.
(2)在第一象限的抛物线上求点P,使得S△PBC最大.
(3)点P是抛物线上x轴上方一点,若∠CAP=45°,求P点坐标.
浙江省2024年九年级上册第1次月考模拟考试卷
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.下列函数关系中,y是x的二次函数的是( )
A.y=50+x2 B.
C.y=3x+4 D.y=(x+2)(x﹣3)﹣x2
【分析】根据二次函数的定义:形如y=ax2+bx+c(a≠0),这样的函数叫做二次函数,进行判断即可.
【解答】解:A、y=50+x2是二次函数,符合题意;
B、,含有分式,不是二次函数,不符合题意;
C、y=3x+4,是一次函数,不符合题意;
D、y=(x+2)(x﹣3)﹣x2=﹣x﹣6,是一次函数,不符合题意;
故选:A.
2.下列事件中属于必然事件的是( )
A.一个奇数与一个偶数的和为奇数
B.一个三角形三个内角的和小于180°
C.任意抛一枚均匀的硬币,正面朝上
D.有一匹马奔跑的速度是70米/秒
【分析】根据事件发生的可能性大小判断即可.
【解答】解:A、一个奇数与一个偶数的和为奇数,是必然事件,符合题意;
B、一个三角形三个内角的和小于180°,是不可能事件,不符合题意;
C、任意抛一枚均匀的硬币,正面朝上,是随机事件,不符合题意;
D、有一匹马奔跑的速度是70米/秒,是不可能事件,不符合题意;
故选:A.
3.已知⊙O的半径为8cm,点P在⊙O上,则OP的长为( )
A.2cm B.4cm C.8cm D.16cm
【分析】根据点在圆上,点到圆心的距离等于圆的半径求解.
【解答】解:∵点P在⊙O上,
∴OP=8cm.
故选:C.
4.如图四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转72°后,能与原图形完全重合的是( )
A. B.
C. D.
【分析】观察图形,从图形的性质可以确定旋转角,然后进行判断即可得到答案.
【解答】解:A图形顺时针旋转120°后,能与原图形完全重合,A不正确;
B图形顺时针旋转90°后,能与原图形完全重合,B不正确;
C图形顺时针旋转180°后,能与原图形完全重合,C不正确;
D图形顺时针旋转72°后,能与原图形完全重合,D正确,
故选:D.
5.下列命题中,正确的是( )
A.任意三点确定一个圆
B.平分弦的直径垂直于弦
C.圆既是轴对称图形又是中心对称图形
D.垂直弦的直线必过圆心
【分析】根据不共线的三点确定一个圆、垂径定理的推论和圆的有关性质分别判断.
【解答】解:不共线的三点确定一个圆,所以A选项不正确;
平分(非直径)弦的直径垂直于弦,所以B选项不正确;
圆既是轴对称图形又是中心对称图形,过圆心的直线都是它的对称轴,圆心是它的对称中心,所以C选项正确;
弦的垂直平分线必过圆心,所以D选项不正确;
故选:C.
6.对于y=﹣2(x﹣3)2+2的图象下列叙述正确的是( )
A.顶点坐标为(﹣3,2)
B.对称轴为:直线x=﹣3
C.当x≥3时y随x增大而减小
D.函数的最小值是2
【分析】由抛物线解析式可求得其顶点坐标、对称轴、开口方向,进一步可求得其最值及增减性.
【解答】解:
∵y=﹣2(x﹣3)2+2,
∴抛物线开口向下,顶点坐标为(3,2),对称轴为x=3,当x=3时,函数有最大值2,
∴A、B、D不正确;
∵对称轴为x=3,且开口向下,
∴当x≥3时y随x的增大而减小,
故选:C.
7.某校计划组织研学活动,现有四个地点可供选择:毛店、森山小镇、八都水库、德胜岩,若从中随机选择一个地点,则选中“八都水库”或“毛店”的概率为( )
A. B. C. D.
【分析】根据概率公式可直接求解.
【解答】解:∵有四个地点可供选择:毛店、森山小镇、八都水库、德胜岩,
∴若从中随机选择一个地点,则选中“八都水库”或“毛店”的概率为;
故选:C.
8.已知k是不为0的常数,则函数y=kx与y=kx2+k2的图象可能是( )
A. B.
C. D.
【分析】分两种情况进行讨论:k>0与k<0进行讨论即可.
【解答】解:当k>0时,抛物线y=kx2+k2开口向上,与y轴正半轴相交,函数y=kx经过第一、三象限,选项中没有符合的;
当k<0时,抛物线y=kx2+k2开口向下,与y轴正半轴相交,函数y=kx经过第二、四象限,故A选项符合题意;
故选:A.
9.如图,D是等边△ABC外接圆上的点,且∠DAC=20°,则∠ACD的度数为( )
A.20° B.30° C.40° D.45°
【分析】根据圆内接四边形的性质得到∠D=180°﹣∠B=120°,根据三角形内角和定理计算即可.
【解答】解:∵△ABC是等边三角形,
∴∠B=60°,
∵四边形ABCD是圆内接四边形,
∴∠D=180°﹣∠B=120°,
∴∠ACD=180°﹣∠DAC﹣∠D=40°,
故选:C.
10.二位同学在研究函数y=a(x+3)(x﹣)(a为实数,且a≠0)时,甲发现当0<a<1时,函数图象的顶点在第四象限;乙发现方程a(x+3)(x﹣)+5=0必有两个不相等的实数根.则( )
A.甲、乙的结论都错误
B.甲的结论正确,乙的结论错误
C.甲、乙的结论都正确
D.甲的结论错误,乙的结论正确
【分析】由函数解析式确定函数与x轴的两个交点的横坐标分别是﹣3和,再由函数的对称性确定函数顶点的横坐标为,根据甲的说法求0<a<1时的范围,即可确定甲的说法错误;将方程a(x+3)(x﹣)+5=0化为一元二次方程ax2+(3a﹣2)x﹣1=0,求判别式Δ=9(a﹣)2+>0,即可确定方程的根的情况.
【解答】解:由函数y=a(x+3)(x﹣)可知,函数与x轴的两个交点的横坐标分别是﹣3和,
∴函数顶点的横坐标为,
∵0<a<1,
∴>﹣,
∴函数的顶点不一定在第四象限,故甲的结论错误;
∵a(x+3)(x﹣)+5=0可以化为ax2+(3a﹣2)x﹣1=0,
Δ=(3a﹣2)2+4a=9a2﹣8a+4=9(a﹣)2+>0,
∴a(x+3)(x﹣)+5=0必有两个不相等的实数根,
故乙的结论正确;
故选:D.
二.填空题(共6小题,满分24分,每小题4分)
11.如图,转盘中黄色扇形的圆心角为90°,绿色扇形的圆心角为270°,现让转盘自由转动两次,则两次指针都落在绿色区域的概率为 .(注:当指针恰好指在分界线上时,无效重转)
【分析】通过计算转盘的黄色扇形和绿色扇形的面积之比可得到2次指针都落在绿色区域的概率.
【解答】解:由图得:黄色扇形的圆心角为90°,绿色扇形的圆心角是270°,
∴黄色扇形的面积:绿色扇形的面积=,
如图,
故让转盘自由转动2次,2次指针都落在绿色区域的概率是.
故答案为:.
12.圆内接正方形的每条边所对的圆心角的度数是 90° .
【分析】根据圆内接正方形的中心角的概念计算即可.
【解答】解:圆内接正方形的一条边所对的圆心角的度数为:,
故答案为:90°.
13.已知二次函数y=x2+6x.点A(2,m)与点B(n,4)关于该函数图象的对称轴对称,那么m+n= ﹣4 .
【分析】首先求出抛物线y=x2+6x的对称轴,然后根据点A(2,m)与点B(n,4)关于该抛物线的对称轴对称,即可求出m+n的值.
【解答】解:∵抛物线解析式为y=x2+6x,
∴抛物线的对称轴x=﹣3,
∵点A(2,m)与点B(n,4)关于该抛物线的对称轴对称,
∴2+n=﹣6,m=4,
解得n=﹣8,
故m+n=4﹣8=﹣4,
故答案为:﹣4.
14.若二次函数y=ax2﹣bx﹣1的图象经过点(2,1),则2023﹣2a+b= 2022 .
【分析】把点(2,1)代入函数解析式求出2a﹣b=1,然后即可得解.
【解答】解:∵y=ax2﹣bx﹣1的图象经过点(2,1),
∴4a﹣2b﹣1=1,
∴2a﹣b=1,
∴2023﹣2a+b=2023﹣(2a﹣b)=2023﹣1=2022,
故答案为:2022.
15.已知二次函数y1=ax2+bx+c与一次函数y2=kx+m(k≠0)的图象相交于点A(﹣2,4),B(8,2).如图所示,则能使y1>y2成立的x的取值范围是 x<﹣2或x>8 .
【分析】直接根据函数的图象即可得出结论.
【解答】解:∵由函数图象可知,当x<﹣2或x>8时,一次函数的图象在二次函数的下方,
∴能使y1>y2成立的x的取值范围是x<﹣2或x>8.
故答案为:x<﹣2或x>8.
16.如图,在扇形AOB中,∠AOB=90°,点C在,=2,OA=3,CD⊥OB于点D,则图中阴影部分的面积为 π﹣ .
【分析】连接OC,AC,由点C为的三等分点,∠AOB=90°,得到∠COD=30°,∠AOC=60°,根据CD⊥OB,得到S△OCD=S△ACD,根据扇形和三角形的面积公式即可得到结论.
【解答】解:连接OC,AC,
∵点C为
的三等分点,∠AOB=90°,
∴∠COD=30°,∠AOC=60°,
∵CD⊥OB,
∴S△OCD=S△ACD,
∵∠CDO=90°,∠DOC=30°,OC=OA=3,
∴CD=,OD=,
∴图中阴影部分的面积=S△ACD+S弓形AC=+××+﹣×3×=﹣,
故答案为:π﹣.
三.解答题(共7小题,满分66分)
17.(8分)二次函数y=ax2+bx+c的自变量x与函数值y的对应值如表,根据下表回答问题.
x ﹣3 ﹣2 ﹣1 0
y ﹣2 ﹣2 0 4
(1)求出该二次函数的表达式;
(2)向下平移该二次函数,使其经过原点,求出平移后图象所对应的二次函数表达式.
【分析】(1)把(﹣2,﹣2),(﹣1,0),(0,4)代入二次函数y=ax2+bx+c,即可求出a、b、c的值,进而得出函数的解析式;
(2)结合(1)中求得的抛物线解析式即可得到平移后图象所对应的二次函数的表达式.
【解答】解:(1)∵(﹣2,﹣2),(﹣1,0),(0,4))均在抛物线y=ax2+bx+c上,
∴,
解得,
∴抛物线的解析式为:y=x2+5x+4;
(2)∵抛物线向下平移4个单位后经过原点.
∴平移后图象所对应的二次函数的表达式是y=x2+5x.
18.(8分)“校园手机”现象越来越受到社会的关注.九(1)班学生在“统计实习”实践活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图:
(1)在图②中,AB是⊙O的直径,求这次调查的家长总人数,并补全图①;
(2)求图②中表示家长“基本赞成”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“无所谓”态度的家长的概率是多少?
【分析】(1)根据两个统计图可知,“不赞成”的有200人,占调查人数的50%,可求出调查人数,再求出“基本赞成”的人数,补全统计图;
(2)求出“基本赞成”所占的百分比,进而求出相应圆心角的度数;
(3)根据概率的定义进行计算即可.
【解答】解:(1)由于AB是⊙O的直径,所以“不赞成”占调查总人数的50%,
200÷50%=400(人),
样本中“非常赞成”的人数:400×26%=104(人),
“基本赞成”的人数为:400﹣200﹣104﹣16=80(人),
补全的统计图如下:
(2)360°×=72°,
答:图②中表示家长“基本赞成”的圆心角的度数为72°;
(3)样本中,被调查的400名家长中,“无所谓”的有16名,
所以随机抽查一个,恰好是“无所谓”态度的家长的概率是=,
答:随机抽查一个,恰好是“无所谓”态度的家长的概率是.
19.(8分)某网店专售一种杭州亚运会纪念品,其成本为每件60元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品每件获利不得高于50%据市场调查发现,若每件销售价70元,月销售量450件,每增加1元,月销量减少5件.
(1)若每件销售价80元,则每月可得利润 8000 元;
(2)设每件商品销售价为x元,该网店每月获得的利润为w元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
【分析】(1)根据利润=每件利润×月销售量即可得出答案;
(2)设每件商品销售价为x元,则每件的利润为(x﹣60)元,销售量为450﹣5×(x﹣70)=800﹣5x(件),根据“月利润=每件利润×月销售量”列出函数解析式,配方成顶点式后依据二次函数的性质求解即可得出答案.
【解答】解:(1)若每件销售价80元,则每月可得利润(80﹣60)×(450﹣5×10)=8000(元),
故答案为:8000;
(2)设每件商品销售价为x元,
则每件的利润为(x﹣60)元,销售量为450﹣5×(x﹣70)=800﹣5x(件),
所以该网店每月获得的利润为w=(x﹣60)(800﹣5x)
=﹣5x2+1100x﹣48000
=﹣5(x﹣110)2+12500,
∵每件获利不得高于50%,
∴x≤60×(1+50%)=90,
∵﹣5<0,
∴当x<110时,w随x的增大而增大,
∴当x=90时,w取得最大值,最大值为10500元.
答:当销售单价为90元时,每月获得的利润最大,最大利润是10500元.
20.(8分)已知一块破损圆形塑胶板,弧上有三点A,B,C.
(1)用尺规作图作出该破损的圆板的圆心,记为点O;
(2)若△ABC为等腰三角形,且AB=AC=5,BC=8,求该圆板的半径.
【分析】(1)作BC、AB的垂直平分线,它们的交点即为圆心O;
(2)连接OA、OB,OA交BC于D点,如图,先利用AB=AC得到=,则根据垂径定理得到∠ADB=∠ODB=90°,BD=CD=BC=4,再利用勾股定理计算出AD=3,设⊙O的半径为r,则OB=r,OD=r﹣3,在Rt△BOD中利用勾股定理得到42+(r﹣3)2=r2,然后解方程即可.
【解答】解:(1)如图,点O为所作;
(2)连接OA、OB,OA交BC于D点,如图,
∵AB=AC,
∴=,
∴OA垂直平分BC,
∴∠ADB=∠ODB=90°,BD=CD=BC=4,
在Rt△ABD中,∵AB=5,BD=4,
∴AD==3,
设⊙O的半径为r,则OB=r,OD=r﹣3,
在Rt△BOD中,42+(r﹣3)2=r2,
解得r=,
即该圆板的半径为.
21.(10分)如图1是城市平直道路,道路限速60km/h.A路口停车线l1和B路口停车线l2之间相距S=400m,A、B两路口各有一个红绿灯.在停车线l1后面停着一辆汽车,该汽车的车头恰好与停车线l1平齐.已知汽车启动后开始加速,加速后汽车行驶的路程S、速度v与时间t的关系分别可以用二次函数和一次函数表示,其图象如图2、3所示.某时刻A路口绿灯亮起,该汽车立即启动.(车身长忽略不计)
(1)求该汽车从停车线l1出发加速到限速所需的时间;
(2)求该汽车最快需要多少时间可以通过停车线l2;
(3)若A路口绿灯亮起29s后B路口绿灯亮起,且B路口绿灯的持续时间为23s.该汽车先加速行驶,然后一直匀速行驶.若该汽车在B路口绿灯期间能顺利通过停车线l2,求该汽车匀速行驶过程中速度的取值范围.
【分析】(1)先将限速单位化为m/s,根据图3求得v=2t,代入求解即可;
(2)根据(1)的结论求得加速时间,根据题意求得运算时间,分别求得两段时间内的路程,进而即可求得答案;
(3)设该汽车匀速行驶过程中的速度为v m/s,根据题意根据(2)的方法求得两段路程所用时间,结合题意中绿灯等亮起期间所用时间,分别列出方程,即可该汽车匀速行驶过程中速度的取值范围.
【解答】解:∵限速为60km/h=m/s,
由图3可知,当t=1时,v=2,
设v=kt,解得k=2,
∴v=2t,
∴t==×=s.
(2)由图2可知,当t=1时,S=1,且x=0时,S=0,
设S=at2,
∴1=a×12,
解得a=1,
∴S=t2(t≥0),
由(1)可知汽车从停车线l1出发加速到限速所需的时间s.
则S=()2=m,
以m/s行驶时间为:=s,
∴+==28s,
∴该汽车最快需要28s可以通过停车线l2;
(3)设该汽车匀速行驶过程中的速度为v m/s,即求出加速到v,
由(1)可得汽车加速到v所用的时间为t=,
则汽车从停车线l1出发加速到v m/s的路程为S=()2,匀速所用的时间为s,
根据题意可得当B路口绿灯亮起时通过,则+=29,
解得v=16或v=100(舍),经检验v=16是原方程的解,
可得当B路口绿灯熄灭时候通过,则+=29+23,
解得v=8或v=200(舍),经检验v=8是原方程的解,
综上所述,该汽车匀速行驶过程中的速度v的范围为8≤v≤16.
22.(12分)有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
(1)如图1,在半对角四边形ABCD中,,,求出∠B与∠C的度数之和;
(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO.∠OBA的平分线交OA于点E,连接DE并延长交AC于点F,若∠AFE=2∠EAF.求证:四边形DBCF是半对角四边形.
【分析】(1)根据半对角四边形的定义和四边形的内角和为360°求解即可;
(2)证明△BDE≌△BOE得出∠BDE=∠BOE,进而可证得∠BDE=2∠C,连接OC,设∠OAC=∠OCA=x,可得∠AFE=2x,∠DFC=180°﹣2x,∠AOC=180°﹣2x=2∠ABC,即可证得结论;
【解答】(1)解:∵在半对角四边形ABCD中,∠B=∠D,∠C=∠A,
∴∠D=2∠B,∠A=2∠C,
∵∠A+2B+∠C+D=360°,
∴3∠B+3∠C=360°,
∴∠B+∠C=120°.
(2)证明:∵BE是∠OBA的平分线,
∴∠DBE=∠OBE,
∵DE=OE,BE=BE,
∴△BDE≌△BOE (SSS),
∴∠BDE=∠BOE,
又∵∠ACB=∠BOA,
∴∠ACB=BDE,
连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
设∠OAC=∠OCA=x,
∵∠AFE=2∠EAF,
∴∠AFE=2x,
∴∠DFC=180°﹣2x,
∵∠AOC=180°﹣2x=2∠ABC,
∴∠DFC=2∠ABC,
∴∠ABC=∠DFC,
∴四边形BCFD是半对角四边形.
23.(12分)如图,二次函数y=(t﹣1)x2+(t+1)x+2(t≠1),x=0与x=3时的函数值相等,其图象与x轴交于A、B两点,与y轴正半轴交于C点.
(1)求二次函数的解析式.
(2)在第一象限的抛物线上求点P,使得S△PBC最大.
(3)点P是抛物线上x轴上方一点,若∠CAP=45°,求P点坐标.
【分析】分析:(1)由x=0与x=3时的函数值相等,列方程求出t值即可求解;
(2)利用待定系数法先求出直线BC的解析式,然后过点P作y轴的平行线,交直线BC于点D,用未知数设出点P、D的坐标,即可得到线段PD的长度表达式,以PD为底、OB为高,即可得到△PBC的面积函数关系式,根据函数的性质即可求出△PBC的面积最大时,点P的坐标;
(3)如图,将AC绕点A顺时针旋转90°得到AC′,则C′(1,﹣1),取CC′的中点H,作直线AH交抛物线于P,则∠CAP=45°,求出直线AH的解析式,利用方程组即可即可求出点P坐标;
【解答】解:(1)∵x=0与x=3时的函数值相等,
∴(t﹣1)×02+(t+1)×0+2=(t﹣1)×32+(t+1)×3+2,
解方程,得t=,
把t=代入二次函数y=(t﹣1)x2+(t+1)x+2(t≠1),
∴二次函数的解析式为:y=.
(2)如图过点P作PD∥y轴,交BC于点D.
把y=0代入y=,得为:=0,
解,得x1=﹣1,x2=4,
∴点A(﹣1,0),B(4,0),
又∵C(0,2)
∴直线BC:y=x+2,
设点P(a,),
把x=a代入y=x+2,y=﹣a+2,
∴点D的坐标为(a,﹣a+2),
∴PD=﹣(﹣a+2)=,
∴S△PBC==×()×4=﹣a2+4a=﹣(a﹣2)2+4,
当a=2时,S△PBC有最大值,最大值为4,
所以点P的坐标(2,3),
(3)如图,将AC绕点A顺时针旋转90°得到AC′,则C′(1,﹣1),取CC′的中点H,作直线AH交抛物线于P,则∠CAP=45°,
∵A(﹣1,0),H(,),
∴直线AH的解析式为y=x+,
由,解得或,
∴P(,).
同课章节目录
