[专项培优]人教版数学九年级上册第22章二次函数培优卷(含答案)
文档属性
| 名称 | [专项培优]人教版数学九年级上册第22章二次函数培优卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 115.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-06 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
[专项培优]人教版数学(2024)九年级上册第22章二次函数培优卷
一、单选题
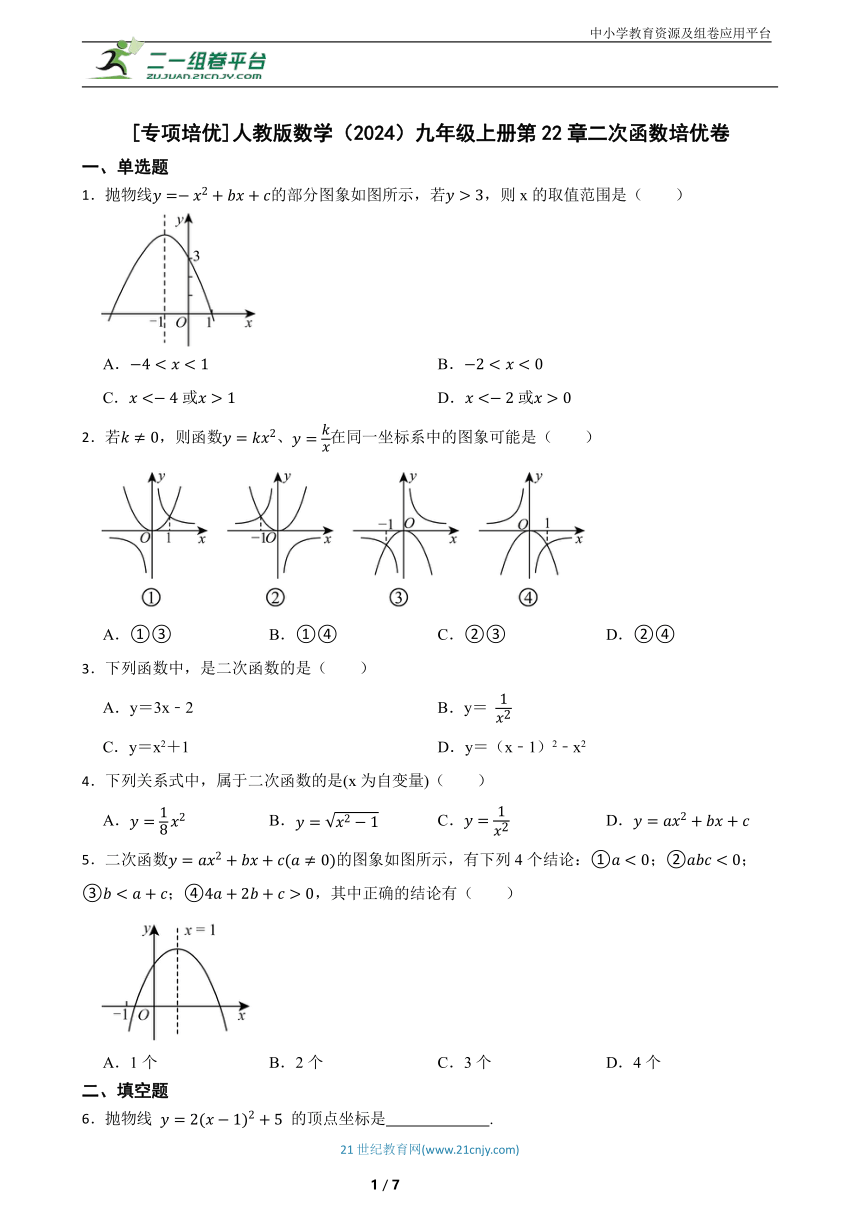
1.抛物线的部分图象如图所示,若,则x的取值范围是( )
A. B.
C.或 D.或
2.若,则函数、在同一坐标系中的图象可能是( )
A.①③ B.①④ C.②③ D.②④
3.下列函数中,是二次函数的是( )
A.y=3x﹣2 B.y=
C.y=x2+1 D.y=(x﹣1)2﹣x2
4.下列关系式中,属于二次函数的是(x为自变量)( )
A. B. C. D.
5.二次函数的图象如图所示,有下列4个结论:①;②;③;④,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
6.抛物线 的顶点坐标是 .
7.二次函数的图象与一次函数的图象如图所示,当时,根据图象写出的取值范围 .
8.顶点是(2,0),且与抛物线 的形状、开口方向都相同的抛物线的解析式为 .
9.已知二次函数的图像经过原点,则a的值是 .
10.将方程x2+x-1=0变形成x2=-x+1,那么方程的解可以看成是y=x2与y= 这两个函数图象的交点的横坐标.
11.将抛物线y=-5x2先向左平移2个单位长度,再向下平移3个单位长度后,得到新的抛物线的表达式是 .
三、计算题
12.数学学习小组的同学共同探究体积为330mL圆柱形有盖容器(如图所示)的设计方案.,他们想探究容器表面积与底面半径的关系.
具体研究过程如下,请补充完整:
(1)建立模型:设该容器的表面积为S,底面半径为cm,高为cm,则
, ①
, ②
由①式得,代入②式得
. ③
可知,S是x的函数,自变量x的取值范围是.
(2)探究函数:
根据函数解析式③,按照下表中自变量x的值计算(精确到个位),得到了S与x的几组对应值:
… 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 …
… 666 454 355 303 277 266 266 274 289 310 336 …
在下面平面直角坐标系中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(3)解决问题:根据图表回答,
①半径为2.4cm的圆柱形容器比半径为4.4cm的圆柱形容器表面积______.(填“大”或“小”);
②若容器的表面积为300,容器底面半径约为______cm(精确到0.1).
13.抛物线y=ax2﹣2x+c与x轴交点坐标为A(﹣1,0),B(3,0),与y轴交点坐标为C(0,n).
(1)求抛物线的解析式;
(2)计算△ABC的面积.
四、解答题
14.为了落实“乡村振兴战略”,我县出台了一系列惠农政策,使农民收入大幅度增加,某农业生产合作社将黑木耳生产加工后进行销售.已知黑木耳的成本价为每盒60元,经市场调查发现,黑木耳每天的销售量y(盒)与销售单价x(元/盒)满足如下关系式:,设该农业生产合作社每天销售黑木耳的利润为w(元).
(1)求w与x之间的函数关系式;
(2)若要使该农业生产合作社每天的销售利润为2500元且最大程度地减少库存,则黑木耳的销售单价为多少元?
(3)若规定黑木耳的销售单价不低于76元,且每天的销售量不少于240盒,则每天销售黑木耳获得的最大利润是多少元?
15.已知二次函数的图象以为顶点,且过点
(1)求该函数的关系式;
(2)点,点在该函数图象上,求m和n的值.
五、综合题
16.2022年教育部正式印发《义务教育课程方案和课程标准(2022年版)》,《劳动》成为一门独立的课程. 某学校率先行动,在校园开辟了一块劳动教育基地,用一段长为30米的篱笆围成一个一边靠墙的矩形养殖园(靠墙的一边不需用篱笆),墙长为16米.
(1)当围成的矩形养殖园面积为108平方米时,求养殖园的边的长;
(2)求矩形养殖园面积的最大值.
17.党的“二十大”期间,某网店直接从工厂以35元/件的进价购进一批纪念“二十大”的钥匙扣,售价为60元/件时,第一天销售了25件.该商品十分畅销,销售量持续走高.在售价不变的基础上,第三天的销售量达到了36件.
(1)求每天销售量的平均增长率.
(2)“二十大”临近结束时,钥匙扣还有大量剩余,为了尽快减少库存,网店打算将钥匙扣降价销售.经调查发现,每降价1元,在第三天的销售量基础上每天可多售2件,将钥匙扣的销售价定为每件多少元时,每天可获得最大利润?最大利润是多少元?
18.已知该酒店有50个房间供游客居住,当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,酒店需对每个房间每天支出20元的各种费用
(1)当房间定价为多少元时,酒店利润最大?
(2)当利润不低于9200元,求房间定价的范围.
六、实践探究题
19.综合与探究
如图,平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴与x轴交于点D.已知,,点P是第一象限抛物线上对称轴右侧的一个动点,设点P的横坐标为m.
(1)求抛物线的函数表达式,并直接写出点C,D的坐标;
(2)连接,求面积的最大值.
答案解析部分
1.【答案】B
【知识点】二次函数图象与坐标轴的交点问题
2.【答案】B
【知识点】二次函数图象与系数的关系
3.【答案】C
【知识点】二次函数的定义
4.【答案】A
【知识点】二次函数的定义
5.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
6.【答案】(1,5)
【知识点】二次函数y=a(x-h)²+k的性质
7.【答案】
【知识点】二次函数与不等式(组)的综合应用;通过函数图象获取信息
8.【答案】
【知识点】二次函数y=a(x-h)²+k的图象
9.【答案】
【知识点】二次函数y=ax²+bx+c的图象
10.【答案】-x+1
【知识点】二次函数与一元二次方程的综合应用
11.【答案】y=-5(x+2)2-3
【知识点】二次函数图象的几何变换
12.【答案】①大;②或
【知识点】利用二次函数图象求一元二次方程的近似根;描点法画函数图象;通过函数图象获取信息
13.【答案】(1)y=x2﹣2x﹣3(2)6
【知识点】待定系数法求二次函数解析式
14.【答案】(1);
(2)黑木耳的销售单价为65元;
(3)每天销售黑木耳获得的最大利润是4480元
【知识点】一元一次不等式组的应用;一元二次方程的实际应用-销售问题;二次函数的实际应用-销售问题
15.【答案】(1)
(2),或.
【知识点】待定系数法求二次函数解析式
16.【答案】(1)12米
(2)平方米
【知识点】一元二次方程的应用-几何问题;二次函数的实际应用-几何问题
17.【答案】(1)
(2)将钥匙扣的销售价定为每件56.5元时,每天可获得最大利润,最在利润是9 元
【知识点】一元二次方程的实际应用-百分率问题;二次函数的实际应用-销售问题
18.【答案】(1)当房间定价为350元时,酒店利润最大
(2)大于等于元且小于等于480元
【知识点】二次函数的最值;二次函数的实际应用-销售问题
19.【答案】(1)抛物线的函数表达式为,点C的坐标为,点D的坐标为;
(2)面积的最大值为.
【知识点】待定系数法求二次函数解析式;二次函数-面积问题
21世纪教育网(www.21cnjy.com)
1 / 1
[专项培优]人教版数学(2024)九年级上册第22章二次函数培优卷
一、单选题
1.抛物线的部分图象如图所示,若,则x的取值范围是( )
A. B.
C.或 D.或
2.若,则函数、在同一坐标系中的图象可能是( )
A.①③ B.①④ C.②③ D.②④
3.下列函数中,是二次函数的是( )
A.y=3x﹣2 B.y=
C.y=x2+1 D.y=(x﹣1)2﹣x2
4.下列关系式中,属于二次函数的是(x为自变量)( )
A. B. C. D.
5.二次函数的图象如图所示,有下列4个结论:①;②;③;④,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
6.抛物线 的顶点坐标是 .
7.二次函数的图象与一次函数的图象如图所示,当时,根据图象写出的取值范围 .
8.顶点是(2,0),且与抛物线 的形状、开口方向都相同的抛物线的解析式为 .
9.已知二次函数的图像经过原点,则a的值是 .
10.将方程x2+x-1=0变形成x2=-x+1,那么方程的解可以看成是y=x2与y= 这两个函数图象的交点的横坐标.
11.将抛物线y=-5x2先向左平移2个单位长度,再向下平移3个单位长度后,得到新的抛物线的表达式是 .
三、计算题
12.数学学习小组的同学共同探究体积为330mL圆柱形有盖容器(如图所示)的设计方案.,他们想探究容器表面积与底面半径的关系.
具体研究过程如下,请补充完整:
(1)建立模型:设该容器的表面积为S,底面半径为cm,高为cm,则
, ①
, ②
由①式得,代入②式得
. ③
可知,S是x的函数,自变量x的取值范围是.
(2)探究函数:
根据函数解析式③,按照下表中自变量x的值计算(精确到个位),得到了S与x的几组对应值:
… 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 …
… 666 454 355 303 277 266 266 274 289 310 336 …
在下面平面直角坐标系中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(3)解决问题:根据图表回答,
①半径为2.4cm的圆柱形容器比半径为4.4cm的圆柱形容器表面积______.(填“大”或“小”);
②若容器的表面积为300,容器底面半径约为______cm(精确到0.1).
13.抛物线y=ax2﹣2x+c与x轴交点坐标为A(﹣1,0),B(3,0),与y轴交点坐标为C(0,n).
(1)求抛物线的解析式;
(2)计算△ABC的面积.
四、解答题
14.为了落实“乡村振兴战略”,我县出台了一系列惠农政策,使农民收入大幅度增加,某农业生产合作社将黑木耳生产加工后进行销售.已知黑木耳的成本价为每盒60元,经市场调查发现,黑木耳每天的销售量y(盒)与销售单价x(元/盒)满足如下关系式:,设该农业生产合作社每天销售黑木耳的利润为w(元).
(1)求w与x之间的函数关系式;
(2)若要使该农业生产合作社每天的销售利润为2500元且最大程度地减少库存,则黑木耳的销售单价为多少元?
(3)若规定黑木耳的销售单价不低于76元,且每天的销售量不少于240盒,则每天销售黑木耳获得的最大利润是多少元?
15.已知二次函数的图象以为顶点,且过点
(1)求该函数的关系式;
(2)点,点在该函数图象上,求m和n的值.
五、综合题
16.2022年教育部正式印发《义务教育课程方案和课程标准(2022年版)》,《劳动》成为一门独立的课程. 某学校率先行动,在校园开辟了一块劳动教育基地,用一段长为30米的篱笆围成一个一边靠墙的矩形养殖园(靠墙的一边不需用篱笆),墙长为16米.
(1)当围成的矩形养殖园面积为108平方米时,求养殖园的边的长;
(2)求矩形养殖园面积的最大值.
17.党的“二十大”期间,某网店直接从工厂以35元/件的进价购进一批纪念“二十大”的钥匙扣,售价为60元/件时,第一天销售了25件.该商品十分畅销,销售量持续走高.在售价不变的基础上,第三天的销售量达到了36件.
(1)求每天销售量的平均增长率.
(2)“二十大”临近结束时,钥匙扣还有大量剩余,为了尽快减少库存,网店打算将钥匙扣降价销售.经调查发现,每降价1元,在第三天的销售量基础上每天可多售2件,将钥匙扣的销售价定为每件多少元时,每天可获得最大利润?最大利润是多少元?
18.已知该酒店有50个房间供游客居住,当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,酒店需对每个房间每天支出20元的各种费用
(1)当房间定价为多少元时,酒店利润最大?
(2)当利润不低于9200元,求房间定价的范围.
六、实践探究题
19.综合与探究
如图,平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴与x轴交于点D.已知,,点P是第一象限抛物线上对称轴右侧的一个动点,设点P的横坐标为m.
(1)求抛物线的函数表达式,并直接写出点C,D的坐标;
(2)连接,求面积的最大值.
答案解析部分
1.【答案】B
【知识点】二次函数图象与坐标轴的交点问题
2.【答案】B
【知识点】二次函数图象与系数的关系
3.【答案】C
【知识点】二次函数的定义
4.【答案】A
【知识点】二次函数的定义
5.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
6.【答案】(1,5)
【知识点】二次函数y=a(x-h)²+k的性质
7.【答案】
【知识点】二次函数与不等式(组)的综合应用;通过函数图象获取信息
8.【答案】
【知识点】二次函数y=a(x-h)²+k的图象
9.【答案】
【知识点】二次函数y=ax²+bx+c的图象
10.【答案】-x+1
【知识点】二次函数与一元二次方程的综合应用
11.【答案】y=-5(x+2)2-3
【知识点】二次函数图象的几何变换
12.【答案】①大;②或
【知识点】利用二次函数图象求一元二次方程的近似根;描点法画函数图象;通过函数图象获取信息
13.【答案】(1)y=x2﹣2x﹣3(2)6
【知识点】待定系数法求二次函数解析式
14.【答案】(1);
(2)黑木耳的销售单价为65元;
(3)每天销售黑木耳获得的最大利润是4480元
【知识点】一元一次不等式组的应用;一元二次方程的实际应用-销售问题;二次函数的实际应用-销售问题
15.【答案】(1)
(2),或.
【知识点】待定系数法求二次函数解析式
16.【答案】(1)12米
(2)平方米
【知识点】一元二次方程的应用-几何问题;二次函数的实际应用-几何问题
17.【答案】(1)
(2)将钥匙扣的销售价定为每件56.5元时,每天可获得最大利润,最在利润是9 元
【知识点】一元二次方程的实际应用-百分率问题;二次函数的实际应用-销售问题
18.【答案】(1)当房间定价为350元时,酒店利润最大
(2)大于等于元且小于等于480元
【知识点】二次函数的最值;二次函数的实际应用-销售问题
19.【答案】(1)抛物线的函数表达式为,点C的坐标为,点D的坐标为;
(2)面积的最大值为.
【知识点】待定系数法求二次函数解析式;二次函数-面积问题
21世纪教育网(www.21cnjy.com)
1 / 1
同课章节目录
