12.3角的平分线的性质 同步练习(含简单答案) 人教版八年级数学上册
文档属性
| 名称 | 12.3角的平分线的性质 同步练习(含简单答案) 人教版八年级数学上册 | 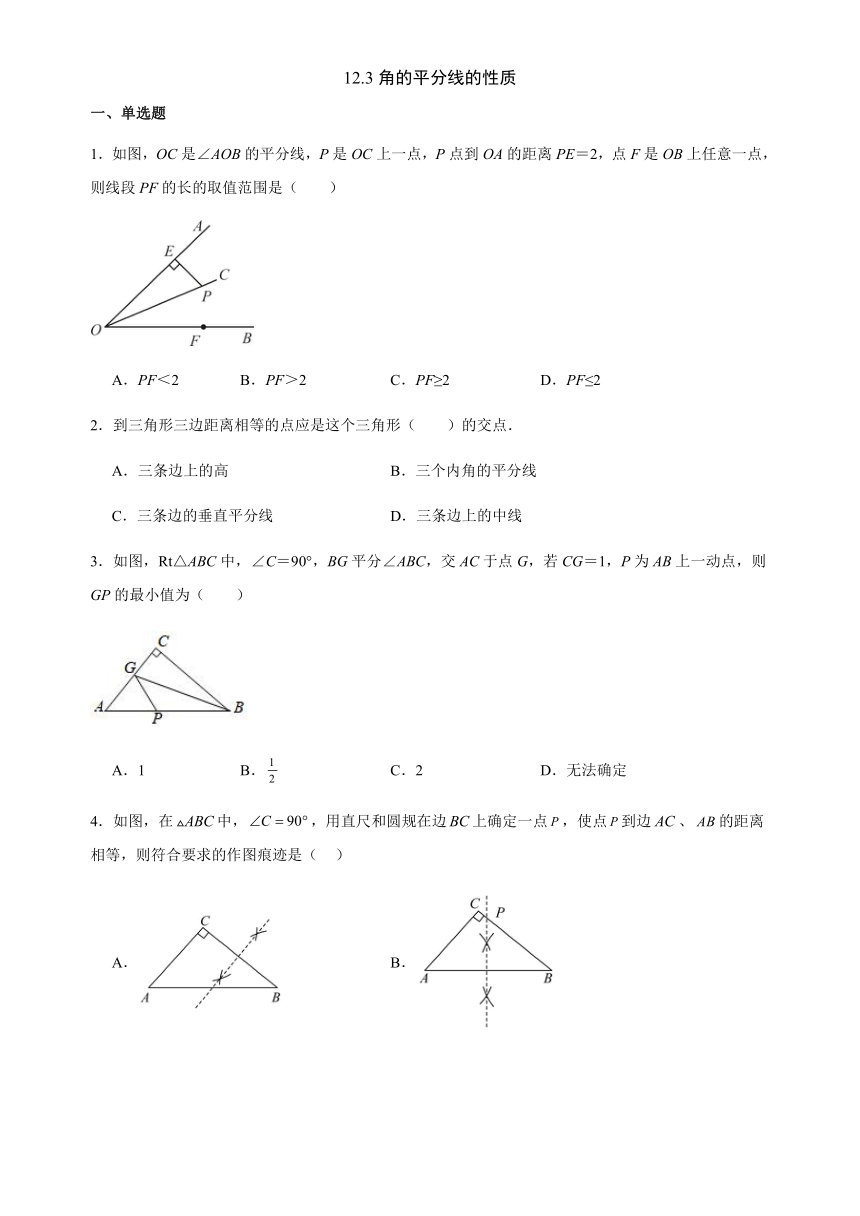 | |
| 格式 | docx | ||
| 文件大小 | 341.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-06 17:36:58 | ||
图片预览


文档简介
12.3角的平分线的性质
一、单选题
1.如图,OC是∠AOB的平分线,P是OC上一点,P点到OA的距离PE=2,点F是OB上任意一点,则线段PF的长的取值范围是( )
A.PF<2 B.PF>2 C.PF≥2 D.PF≤2
2.到三角形三边距离相等的点应是这个三角形( )的交点.
A.三条边上的高 B.三个内角的平分线
C.三条边的垂直平分线 D.三条边上的中线
3.如图,Rt△ABC中,∠C=90°,BG平分∠ABC,交AC于点G,若CG=1,P为AB上一动点,则GP的最小值为( )
A.1 B. C.2 D.无法确定
4.如图,在中,,用直尺和圆规在边上确定一点,使点到边、的距离相等,则符合要求的作图痕迹是( )
A. B.
C. D.
5.如图,在中,,AD平分,,,那么点D到直线AB的距离是( )
A.2cm B.4cm C.6cm D.10cm
6.如图,在△ABC中,BD是AC边上的高,AE平分∠CAB,交BD于点E,AB=8,DE=3,则△ABE的面积等于( )
A.15 B.12 C.10 D.14
7.如图,在四边形中,,连接.若P是边上一动点,则长的最小值为( ).
A.4 B.3 C.2 D.1
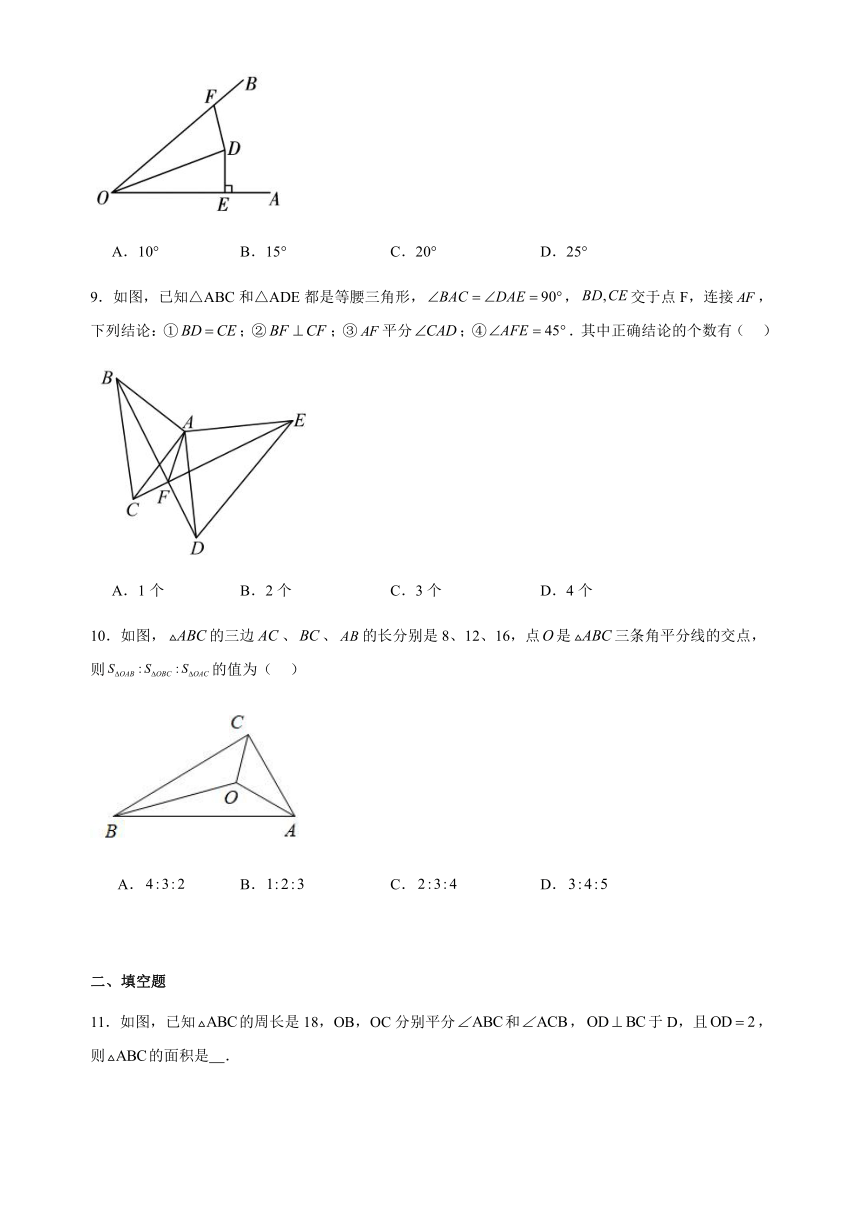
8.如图,,点D在的内部,连接,过点D作于点E,F为上一动点,连接,若DF的最小值与DF相等,则的度数为( )
A.10° B.15° C.20° D.25°
9.如图,已知△ABC和△ADE都是等腰三角形,,交于点F,连接,下列结论:①;②;③平分;④.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
10.如图,的三边、、的长分别是8、12、16,点是三条角平分线的交点,则的值为( )
A. B. C. D.
二、填空题
11.如图,已知的周长是18,OB,OC分别平分和,于D,且,则的面积是 .
12.如图,正方形的边长为4,是的平分线,交于点,若,则点到的距离为 .
13.已知∠AOB=60°,以O为圆心,以任意长为半径作弧,交OA,OB于点M,N,分别以点M,N为圆心,以大于MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为 .
14.如图,已知的周长是20,、分别平分和,于,若的面积是30,则 .
15.如图,,,分别平分和,,垂足为,如果,那么与的距离是
16.如图,已知点D是△ABC的两外角平分线的交点,下列说法:
(1) AD=CD;(2)D到AB、BC的距离相等;(3) D到△ABC的三边的距离相等;(4) 点D在∠B的平分线上; 其中正确的说法的序号是 .
17.如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,连接AP,交CD于点M,若∠ACD=110°,求∠CMA的度数 .
三、解答题
18.如图,O是AB上一点,过点O作射线OC.
(1)利用尺规作图分别作∠AOC和∠BOC的平分线OD,OE(保留作图痕迹,不写作法).
(2)试判断OD与OE的位置关系,并说明理由.
19.如图,射线OA、OC在射线OB的异侧且∠BOC=2∠AOB(∠AOB<60°),射线OD平分∠AOC,请探求∠BOD与∠AOB的数量关系.
20.如图,已知O为坐标原点,B(0 ,3),OB=CD,且OD=2OC,将△BOC沿BC翻折至△BEC,使得点E、O重合,点M是y轴正半轴上的一点且位于点B上方,以点B为端点作一条射线BA,使∠MBA=∠BCO,点F是射线BA上的一点.
(1)请直接写出C、D两点的坐标:点C ,点D ;
(2)当BF=BC时,连接FE.
①求点F的坐标;
②求此时△BEF的面积.
21.在四边形ABCD中,AC平分∠DAB,∠ABC=α,∠ADC=180°﹣α.
(1)若α=90°时,直接写出CD与CB的数量关系为 ;
(2)如图1,当α≠90°时,(1)中结论是否还成立,说明理由;
(3)如图2,O为AC中点,M为AB上一点,BM=AD,求的值.
参考答案:
1.C
2.B
3.A
4.C
5.B
6.B
7.A
8.C
9.C
10.A
11.18
12.
13.或
14.3
15.
16.(2),(3),(4)
17.∠CMA =35°.
18.OD⊥OE
19.∠AOB=2∠BOD.
20.(1)(-1 ,0),(2 ,0);(2)①F(-3 ,4);②.
21.(1)CD=CB;(2)仍然有CD=CB;(3)=2.
一、单选题
1.如图,OC是∠AOB的平分线,P是OC上一点,P点到OA的距离PE=2,点F是OB上任意一点,则线段PF的长的取值范围是( )
A.PF<2 B.PF>2 C.PF≥2 D.PF≤2
2.到三角形三边距离相等的点应是这个三角形( )的交点.
A.三条边上的高 B.三个内角的平分线
C.三条边的垂直平分线 D.三条边上的中线
3.如图,Rt△ABC中,∠C=90°,BG平分∠ABC,交AC于点G,若CG=1,P为AB上一动点,则GP的最小值为( )
A.1 B. C.2 D.无法确定
4.如图,在中,,用直尺和圆规在边上确定一点,使点到边、的距离相等,则符合要求的作图痕迹是( )
A. B.
C. D.
5.如图,在中,,AD平分,,,那么点D到直线AB的距离是( )
A.2cm B.4cm C.6cm D.10cm
6.如图,在△ABC中,BD是AC边上的高,AE平分∠CAB,交BD于点E,AB=8,DE=3,则△ABE的面积等于( )
A.15 B.12 C.10 D.14
7.如图,在四边形中,,连接.若P是边上一动点,则长的最小值为( ).
A.4 B.3 C.2 D.1
8.如图,,点D在的内部,连接,过点D作于点E,F为上一动点,连接,若DF的最小值与DF相等,则的度数为( )
A.10° B.15° C.20° D.25°
9.如图,已知△ABC和△ADE都是等腰三角形,,交于点F,连接,下列结论:①;②;③平分;④.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
10.如图,的三边、、的长分别是8、12、16,点是三条角平分线的交点,则的值为( )
A. B. C. D.
二、填空题
11.如图,已知的周长是18,OB,OC分别平分和,于D,且,则的面积是 .
12.如图,正方形的边长为4,是的平分线,交于点,若,则点到的距离为 .
13.已知∠AOB=60°,以O为圆心,以任意长为半径作弧,交OA,OB于点M,N,分别以点M,N为圆心,以大于MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为 .
14.如图,已知的周长是20,、分别平分和,于,若的面积是30,则 .
15.如图,,,分别平分和,,垂足为,如果,那么与的距离是
16.如图,已知点D是△ABC的两外角平分线的交点,下列说法:
(1) AD=CD;(2)D到AB、BC的距离相等;(3) D到△ABC的三边的距离相等;(4) 点D在∠B的平分线上; 其中正确的说法的序号是 .
17.如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,连接AP,交CD于点M,若∠ACD=110°,求∠CMA的度数 .
三、解答题
18.如图,O是AB上一点,过点O作射线OC.
(1)利用尺规作图分别作∠AOC和∠BOC的平分线OD,OE(保留作图痕迹,不写作法).
(2)试判断OD与OE的位置关系,并说明理由.
19.如图,射线OA、OC在射线OB的异侧且∠BOC=2∠AOB(∠AOB<60°),射线OD平分∠AOC,请探求∠BOD与∠AOB的数量关系.
20.如图,已知O为坐标原点,B(0 ,3),OB=CD,且OD=2OC,将△BOC沿BC翻折至△BEC,使得点E、O重合,点M是y轴正半轴上的一点且位于点B上方,以点B为端点作一条射线BA,使∠MBA=∠BCO,点F是射线BA上的一点.
(1)请直接写出C、D两点的坐标:点C ,点D ;
(2)当BF=BC时,连接FE.
①求点F的坐标;
②求此时△BEF的面积.
21.在四边形ABCD中,AC平分∠DAB,∠ABC=α,∠ADC=180°﹣α.
(1)若α=90°时,直接写出CD与CB的数量关系为 ;
(2)如图1,当α≠90°时,(1)中结论是否还成立,说明理由;
(3)如图2,O为AC中点,M为AB上一点,BM=AD,求的值.
参考答案:
1.C
2.B
3.A
4.C
5.B
6.B
7.A
8.C
9.C
10.A
11.18
12.
13.或
14.3
15.
16.(2),(3),(4)
17.∠CMA =35°.
18.OD⊥OE
19.∠AOB=2∠BOD.
20.(1)(-1 ,0),(2 ,0);(2)①F(-3 ,4);②.
21.(1)CD=CB;(2)仍然有CD=CB;(3)=2.
