2024~2025学年湖北省武汉市中考数学模拟卷(无答案)
文档属性
| 名称 | 2024~2025学年湖北省武汉市中考数学模拟卷(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 363.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-07 00:00:00 | ||
图片预览


文档简介
2024~2025学年武汉市中考数学模拟卷
亲爱的同学,在你答题前,请认真阅读下面的注意事项:
1.本试卷由第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分组成.全卷共6页,三大题,满分120分.考试用时120分钟.
2.答题前,请将你的姓名、准考证号填写在“答题卡”相应位置,并在“答题卡”背面左上角填写姓名和座位号.
3.答第Ⅰ卷(选择题)时,选出每小题答案后,用2B铅笔把“答题卡”上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案.不得答在“试卷”上.
4.答第Ⅱ卷(非选择题)时,答案用0.5毫米黑色笔迹签字笔书写在“答题卡”上.答在“试卷”上无效.
5.认真阅读答题卡上的注意事项.
预祝你取得优异成绩!
第Ⅰ卷(选择题 共30分)
一、选择题(共10小题,每小题3分,共30分)
下列各题中均有四个备选答案,其中有且只有一个是正确的.
1.的相反数是
A. B. C.2 D.-2
2.若分式有意义,则x满足的条件是
A.x=3 B.x<3 C.x>3 D. x≠3
3.已知事件A:小明刚到教室,上课铃声就响了;事件B:掷一枚质地均匀的骰子(骰子的六个面上分别刻有1到6的点数),向上一面的点数不大于6.下列说法正确的是
A.只有事件A是随机事件 B.只有事件B是随机事件
C.都是随机事件 D.都是确定性事件
4.下列交通标志图案中,是中心对称图形的是
A. B. C. D.
5.如图,下列水平放置的几何体中,主视图是三角形的是
A. B. C. D.
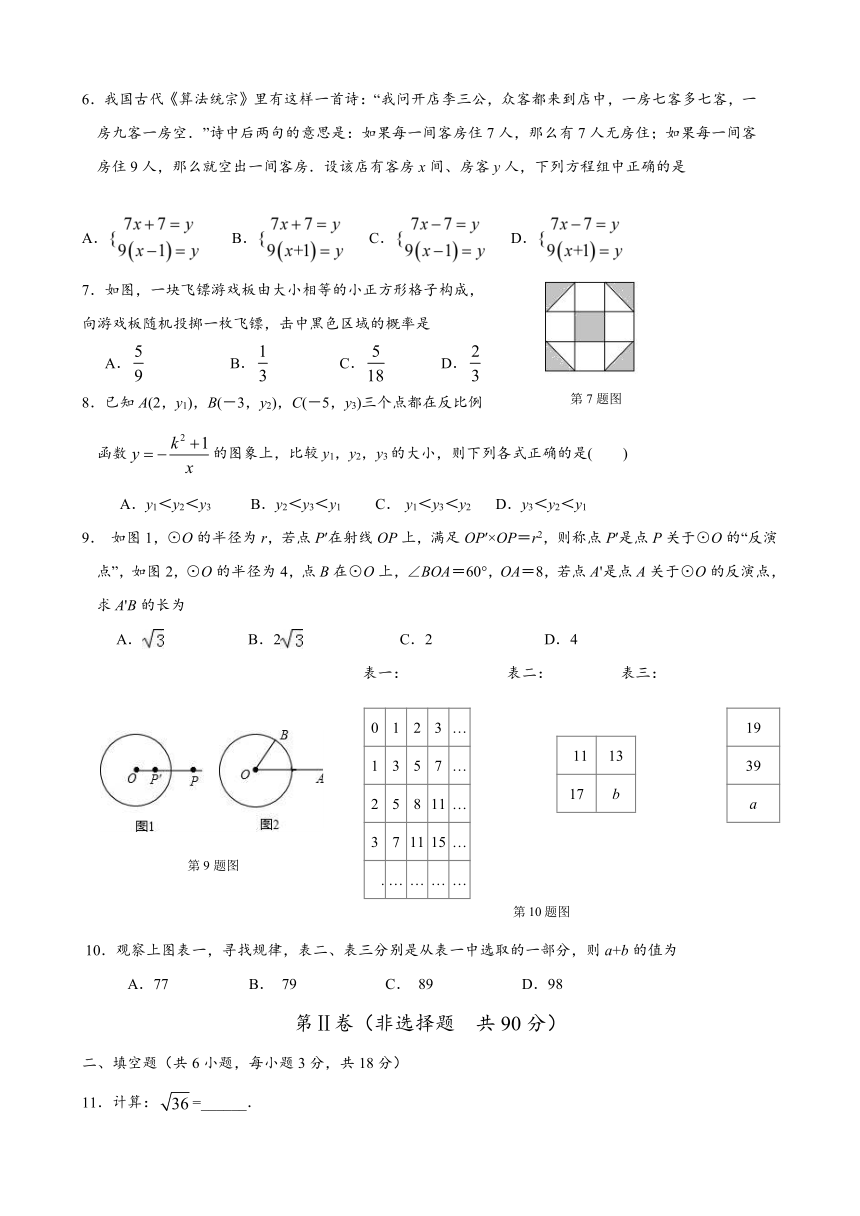
6.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是
A. B. C. D.
7.如图,一块飞镖游戏板由大小相等的小正方形格子构成,
向游戏板随机投掷一枚飞镖,击中黑色区域的概率是
A. B. C. D.
8.已知A(2,y1),B(-3,y2),C(-5,y3)三个点都在反比例
函数的图象上,比较y1,y2,y3的大小,则下列各式正确的是( )
A.y1<y2<y3 B.y2<y3<y1 C. y1<y3<y2 D.y3<y2<y1
9. 如图1,⊙O的半径为r,若点P′在射线OP上,满足OP′×OP=r2,则称点P′是点P关于⊙O的“反演点”,如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A'是点A关于⊙O的反演点,求A'B的长为
A. B.2 C.2 D.4
19
39
a
表一: 表二: 表三:
0 1 2 3 …
1 3 5 7 …
2 5 8 11 …
3 7 11 15 …
… … … … …
11 13
17 b
10.观察上图表一,寻找规律,表二、表三分别是从表一中选取的一部分,则a+b的值为
A.77 B. 79 C. 89 D.98
第Ⅱ卷(非选择题 共90分)
二、填空题(共6小题,每小题3分,共18分)
11.计算:=______.
12.在“爱我中华”中学生演讲比赛中,五位评委分别给选手小明
的评分如下:7,9,6,9,9,则这组数据的中位数是_______.
13.计算:的结果是 .
14.如图所示,△ABC中,AB=AC,过AC上一点E作
DE⊥AC,EF⊥BC,垂足分别为E,F,若∠BDE=140°,
则∠DEF=________.
15.二次函数y=x2+bx的图象如图,对称轴为x=1.若关于x
的一元二次方程x2+bx-2t=0(t为实数)在-1<x≤4的范
围内有解,则t的取值范围是__________.
16.折叠矩形纸片ABCD时,发现可以进行如下操作:
①把△ADE翻折,点A落在DC边上的点F处,
折痕为DE,点E在AB边上;②把纸片展开并铺平;
③把△CDG翻折,点C落在线段AE上的点H处,
折痕为DG,点G在BC边上,若AB=AD+2,
EH=1,则AD=______.
三、解答题(共8小题,共72分)
下列各题解答应写出文字说明、证明过程或演算过程.
17.(本小题满分8分) 计算:a3 a4 a+(a2)4.
18.(本小题满分8分)
如图,已知CB∥DE,∠B+∠D=180°,求证:AB∥CD.
19.(本小题满分8分)为了解取水楼社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中20~60岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
20.(本小题满分8分)
如图,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.
(1)在图中画出以线段AB为一边的矩形ABCD(不是正方形),且点C和点D均在小正方形的顶点上;
(2)在图中画出以线段AB为一腰,底边长为2的等腰三角形ABE,点E在小正方形的顶点上.连接CE,请直接写出线段CE的长 .
21.(本小题满分8分)
如图,AB是半圆O的直径,D为BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC.
(1)求证:CF为⊙O的切线;
(2)若四边形ACFD是平行四边形,求sin∠BAD的值.
22.(本小题满分10分)
某科技开发公司研制出一种新型产品,每件产品的成本为2500元,销售单价定为3200元.在
该产品的试销期间,为了促销,鼓励商家购买该新型品,公司决定商家一次购买这种新型
产品不超过10件时,每件按3200元销售:若一次购买该种产品超过10件时,每多购买一
件,所购买的全部产品的销售单价均降低5元,但销售单价均不低于2800元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2800元?
(2)设商家一次购买这种产品x件,开发公司所获的利润为y元,求y(元)与x(件)
之间的函数关系式,并写出自变量x的取值范围
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着
一次购买的数量的增多,公司所获的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获的利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变)
23.(本小题满分10分)
已知,正方形ABCD中,AB=8,点P是射线BC上的一动点,过点P作PE⊥PA交直线CD于E,连AE.
(1)如图1,若BP=2,求CE的长;
(2)如图2,若AP平分∠BAE,连PD,求tan∠DPE的值;
(3)直线PD、直线AE交于点F,若BC=4PC,则=______.(直接写出结果)
24.(本小题满分12分)
如图,平面直角坐标系中,抛物线y=(x-3a)(x+a)交x轴分别于点A、B(点B在x轴负半轴,OA>OB),交y轴于点C,OC=4OB,连接AC,点P从点A出发向点O运动,点Q从点A出发向点C运动,当一个点到达终点时另一个点也停止运动.
(1)求a的值;
(2)点P,Q都以每秒5个单位长度的速度运动,运动t秒,当点A关于直线PQ对称的点E恰好在抛物线上时,求t的值;
(3)点P以每秒1个单位长度的速度运动,点Q以每秒个单位长度的速度运动,直线PQ交抛物线于点M,当△CMA的内心在直线PQ上时,求点M的坐标.
亲爱的同学,在你答题前,请认真阅读下面的注意事项:
1.本试卷由第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分组成.全卷共6页,三大题,满分120分.考试用时120分钟.
2.答题前,请将你的姓名、准考证号填写在“答题卡”相应位置,并在“答题卡”背面左上角填写姓名和座位号.
3.答第Ⅰ卷(选择题)时,选出每小题答案后,用2B铅笔把“答题卡”上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案.不得答在“试卷”上.
4.答第Ⅱ卷(非选择题)时,答案用0.5毫米黑色笔迹签字笔书写在“答题卡”上.答在“试卷”上无效.
5.认真阅读答题卡上的注意事项.
预祝你取得优异成绩!
第Ⅰ卷(选择题 共30分)
一、选择题(共10小题,每小题3分,共30分)
下列各题中均有四个备选答案,其中有且只有一个是正确的.
1.的相反数是
A. B. C.2 D.-2
2.若分式有意义,则x满足的条件是
A.x=3 B.x<3 C.x>3 D. x≠3
3.已知事件A:小明刚到教室,上课铃声就响了;事件B:掷一枚质地均匀的骰子(骰子的六个面上分别刻有1到6的点数),向上一面的点数不大于6.下列说法正确的是
A.只有事件A是随机事件 B.只有事件B是随机事件
C.都是随机事件 D.都是确定性事件
4.下列交通标志图案中,是中心对称图形的是
A. B. C. D.
5.如图,下列水平放置的几何体中,主视图是三角形的是
A. B. C. D.
6.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是
A. B. C. D.
7.如图,一块飞镖游戏板由大小相等的小正方形格子构成,
向游戏板随机投掷一枚飞镖,击中黑色区域的概率是
A. B. C. D.
8.已知A(2,y1),B(-3,y2),C(-5,y3)三个点都在反比例
函数的图象上,比较y1,y2,y3的大小,则下列各式正确的是( )
A.y1<y2<y3 B.y2<y3<y1 C. y1<y3<y2 D.y3<y2<y1
9. 如图1,⊙O的半径为r,若点P′在射线OP上,满足OP′×OP=r2,则称点P′是点P关于⊙O的“反演点”,如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A'是点A关于⊙O的反演点,求A'B的长为
A. B.2 C.2 D.4
19
39
a
表一: 表二: 表三:
0 1 2 3 …
1 3 5 7 …
2 5 8 11 …
3 7 11 15 …
… … … … …
11 13
17 b
10.观察上图表一,寻找规律,表二、表三分别是从表一中选取的一部分,则a+b的值为
A.77 B. 79 C. 89 D.98
第Ⅱ卷(非选择题 共90分)
二、填空题(共6小题,每小题3分,共18分)
11.计算:=______.
12.在“爱我中华”中学生演讲比赛中,五位评委分别给选手小明
的评分如下:7,9,6,9,9,则这组数据的中位数是_______.
13.计算:的结果是 .
14.如图所示,△ABC中,AB=AC,过AC上一点E作
DE⊥AC,EF⊥BC,垂足分别为E,F,若∠BDE=140°,
则∠DEF=________.
15.二次函数y=x2+bx的图象如图,对称轴为x=1.若关于x
的一元二次方程x2+bx-2t=0(t为实数)在-1<x≤4的范
围内有解,则t的取值范围是__________.
16.折叠矩形纸片ABCD时,发现可以进行如下操作:
①把△ADE翻折,点A落在DC边上的点F处,
折痕为DE,点E在AB边上;②把纸片展开并铺平;
③把△CDG翻折,点C落在线段AE上的点H处,
折痕为DG,点G在BC边上,若AB=AD+2,
EH=1,则AD=______.
三、解答题(共8小题,共72分)
下列各题解答应写出文字说明、证明过程或演算过程.
17.(本小题满分8分) 计算:a3 a4 a+(a2)4.
18.(本小题满分8分)
如图,已知CB∥DE,∠B+∠D=180°,求证:AB∥CD.
19.(本小题满分8分)为了解取水楼社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中20~60岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
20.(本小题满分8分)
如图,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.
(1)在图中画出以线段AB为一边的矩形ABCD(不是正方形),且点C和点D均在小正方形的顶点上;
(2)在图中画出以线段AB为一腰,底边长为2的等腰三角形ABE,点E在小正方形的顶点上.连接CE,请直接写出线段CE的长 .
21.(本小题满分8分)
如图,AB是半圆O的直径,D为BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC.
(1)求证:CF为⊙O的切线;
(2)若四边形ACFD是平行四边形,求sin∠BAD的值.
22.(本小题满分10分)
某科技开发公司研制出一种新型产品,每件产品的成本为2500元,销售单价定为3200元.在
该产品的试销期间,为了促销,鼓励商家购买该新型品,公司决定商家一次购买这种新型
产品不超过10件时,每件按3200元销售:若一次购买该种产品超过10件时,每多购买一
件,所购买的全部产品的销售单价均降低5元,但销售单价均不低于2800元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2800元?
(2)设商家一次购买这种产品x件,开发公司所获的利润为y元,求y(元)与x(件)
之间的函数关系式,并写出自变量x的取值范围
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着
一次购买的数量的增多,公司所获的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获的利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变)
23.(本小题满分10分)
已知,正方形ABCD中,AB=8,点P是射线BC上的一动点,过点P作PE⊥PA交直线CD于E,连AE.
(1)如图1,若BP=2,求CE的长;
(2)如图2,若AP平分∠BAE,连PD,求tan∠DPE的值;
(3)直线PD、直线AE交于点F,若BC=4PC,则=______.(直接写出结果)
24.(本小题满分12分)
如图,平面直角坐标系中,抛物线y=(x-3a)(x+a)交x轴分别于点A、B(点B在x轴负半轴,OA>OB),交y轴于点C,OC=4OB,连接AC,点P从点A出发向点O运动,点Q从点A出发向点C运动,当一个点到达终点时另一个点也停止运动.
(1)求a的值;
(2)点P,Q都以每秒5个单位长度的速度运动,运动t秒,当点A关于直线PQ对称的点E恰好在抛物线上时,求t的值;
(3)点P以每秒1个单位长度的速度运动,点Q以每秒个单位长度的速度运动,直线PQ交抛物线于点M,当△CMA的内心在直线PQ上时,求点M的坐标.
同课章节目录
