人教版数学八上2024-2025学年 第十二章 全等三角形 单元测试卷(无答案)
文档属性
| 名称 | 人教版数学八上2024-2025学年 第十二章 全等三角形 单元测试卷(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 196.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-07 08:32:08 | ||
图片预览

文档简介
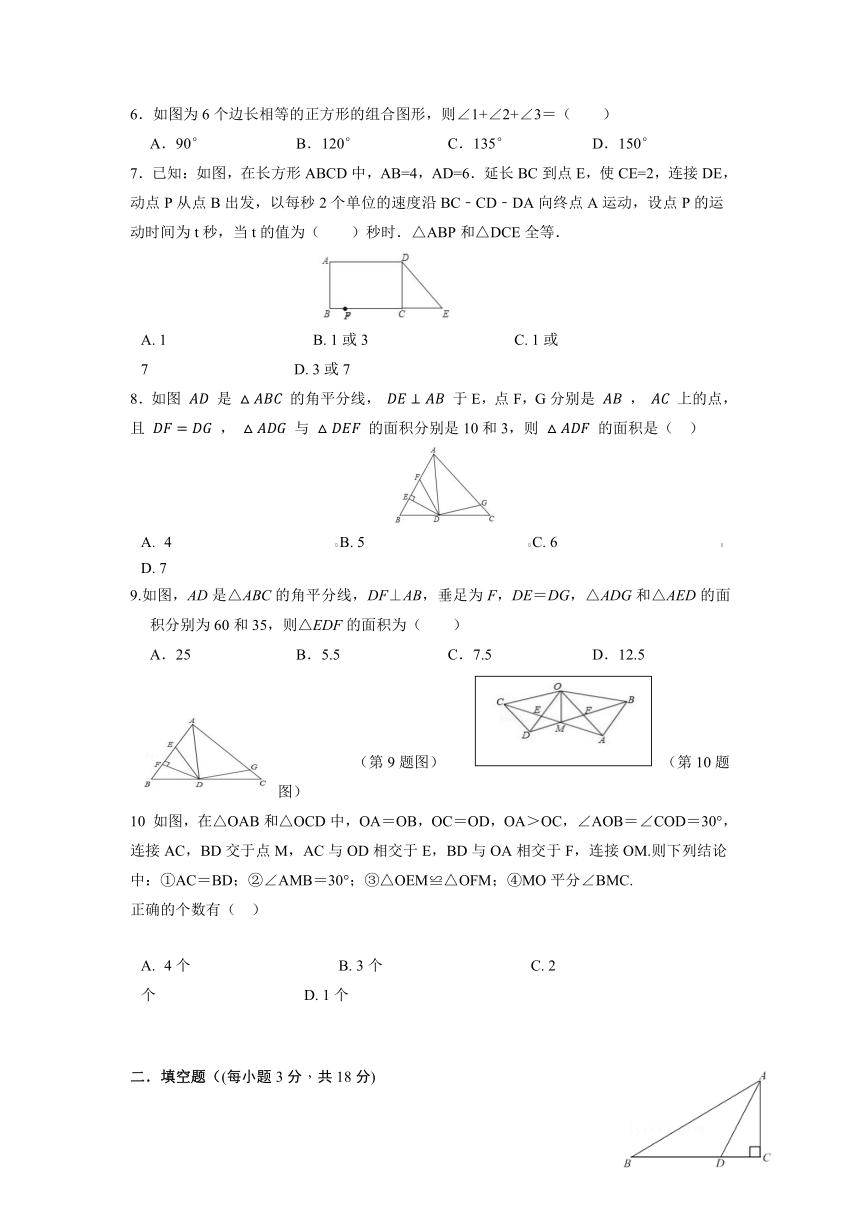
第12章 全等三角形 单元检测卷
考试范围:第十二章 全等三角形,共22题; 考试时间:120分钟; 总分:100分
一.选择题(每题3分,共30分)
1.下列各组两个图形属于全等图形的是( )
A. B.
C. D.
2. 如图,某同学不小心把一块三角形玻璃打碎成三块,现在要到玻璃店配一块与原来完全相同的玻璃,最省事的方法是( )
A. 带①和②去 B. 只带②去 C. 只带③去 D. 都带去
3.如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
A.∠M=∠N B.AB=CD C.AM=CN D.AM∥CN
4.如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线,这条射线就是角的平分线,在这个操作过程中,运用了三角形全等的判定方法是( )
A.SSS B.SAS C.ASA D.AAS
(第4题图) (第5题图)(第6题图)
5.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B.7 C.5 D.4
6.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )
A.90° B.120° C.135° D.150°
7.已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.
A. 1 B. 1或3 C. 1或7 D. 3或7
8.如图 是 的角平分线, 于E,点F,G分别是 , 上的点,且 , 与 的面积分别是10和3,则 的面积是( )
4 B. 5 C. 6 D. 7
9.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为60和35,则△EDF的面积为( )
A.25 B.5.5 C.7.5 D.12.5
(第9题图) (第10题图)
10 如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=30°,连接AC,BD交于点M,AC与OD相交于E,BD与OA相交于F,连接OM.则下列结论中:①AC=BD;②∠AMB=30°;③△OEM≌△OFM;④MO平分∠BMC.
正确的个数有( )
4个 B. 3个 C. 2个 D. 1个
二.填空题((每小题3分,共18分)
11.如图,在△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,
则△ABD的面积是 .
12.小明沿一段笔直的人行道行走,边走边欣赏风景,在由C走到D的过程中,通过隔离带的空隙P,刚好浏览完对面人行道宣传墙上的一条标语,具体信息如下:如图,AB∥PM∥CD,相邻两平行线间的距离相等,AC,BD相交于P,PD⊥CD垂足为D.已知CD=16米.请根据上述信息求标语AB的长度 .
如图,在 中, , , 平分 交 于点 , 于点 .若 ,则 的周长为________cm.
14. 如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=________.
(第14题图) (第15题图)
15.如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为 .
16.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1 ,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2 ,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3 , …,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En .
若∠En=1度,那∠BEC等于________度。
三.解答题(本题共计6小题,合计52分)
17.(8分)如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,求证:△ADE≌△CFE.
18.(8分)如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
(8分)如图,DE⊥AB,CF⊥AB,垂足分别是点E、F,DE=CF,AE=BF,求证:AC∥BD.
20.(9分)如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长.
21(9分).如图①,点A,E,F,C在同一条直线上,且AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,垂足分别为E,F,AB=CD.
(1)若EF与BD相交于点G,则EG与FG相等吗?请说明理由;
(2)若将图①中△DEC沿AC移动到如图②所示的位置,其余条件不变,则(1)中的结论是否仍成立?不必说明理由.
22.(10分)如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.
①如图1,若∠BCA=90°,α=90°,则BE CF;
②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件 ,使①中的结论仍然成立,并说明理由;
(2)如图3,若线CD经过∠BCA的外部,α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由.
考试范围:第十二章 全等三角形,共22题; 考试时间:120分钟; 总分:100分
一.选择题(每题3分,共30分)
1.下列各组两个图形属于全等图形的是( )
A. B.
C. D.
2. 如图,某同学不小心把一块三角形玻璃打碎成三块,现在要到玻璃店配一块与原来完全相同的玻璃,最省事的方法是( )
A. 带①和②去 B. 只带②去 C. 只带③去 D. 都带去
3.如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
A.∠M=∠N B.AB=CD C.AM=CN D.AM∥CN
4.如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线,这条射线就是角的平分线,在这个操作过程中,运用了三角形全等的判定方法是( )
A.SSS B.SAS C.ASA D.AAS
(第4题图) (第5题图)(第6题图)
5.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B.7 C.5 D.4
6.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )
A.90° B.120° C.135° D.150°
7.已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.
A. 1 B. 1或3 C. 1或7 D. 3或7
8.如图 是 的角平分线, 于E,点F,G分别是 , 上的点,且 , 与 的面积分别是10和3,则 的面积是( )
4 B. 5 C. 6 D. 7
9.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为60和35,则△EDF的面积为( )
A.25 B.5.5 C.7.5 D.12.5
(第9题图) (第10题图)
10 如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=30°,连接AC,BD交于点M,AC与OD相交于E,BD与OA相交于F,连接OM.则下列结论中:①AC=BD;②∠AMB=30°;③△OEM≌△OFM;④MO平分∠BMC.
正确的个数有( )
4个 B. 3个 C. 2个 D. 1个
二.填空题((每小题3分,共18分)
11.如图,在△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,
则△ABD的面积是 .
12.小明沿一段笔直的人行道行走,边走边欣赏风景,在由C走到D的过程中,通过隔离带的空隙P,刚好浏览完对面人行道宣传墙上的一条标语,具体信息如下:如图,AB∥PM∥CD,相邻两平行线间的距离相等,AC,BD相交于P,PD⊥CD垂足为D.已知CD=16米.请根据上述信息求标语AB的长度 .
如图,在 中, , , 平分 交 于点 , 于点 .若 ,则 的周长为________cm.
14. 如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=________.
(第14题图) (第15题图)
15.如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为 .
16.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1 ,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2 ,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3 , …,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En .
若∠En=1度,那∠BEC等于________度。
三.解答题(本题共计6小题,合计52分)
17.(8分)如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,求证:△ADE≌△CFE.
18.(8分)如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
(8分)如图,DE⊥AB,CF⊥AB,垂足分别是点E、F,DE=CF,AE=BF,求证:AC∥BD.
20.(9分)如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长.
21(9分).如图①,点A,E,F,C在同一条直线上,且AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,垂足分别为E,F,AB=CD.
(1)若EF与BD相交于点G,则EG与FG相等吗?请说明理由;
(2)若将图①中△DEC沿AC移动到如图②所示的位置,其余条件不变,则(1)中的结论是否仍成立?不必说明理由.
22.(10分)如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.
①如图1,若∠BCA=90°,α=90°,则BE CF;
②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件 ,使①中的结论仍然成立,并说明理由;
(2)如图3,若线CD经过∠BCA的外部,α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由.
