人教版数学九年级上册 第二十二章 二次函数 单元试卷(含答案)
文档属性
| 名称 | 人教版数学九年级上册 第二十二章 二次函数 单元试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 230.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-07 08:49:47 | ||
图片预览




文档简介
人教版数学九年级上册 第二十二章 二次函数 单元试卷
一、选择题
下列函数是二次函数的是
A. B.
C. D.
由二次函数 可知
A.其图象的开口向下
B.其图象的对称轴为直线
C.其顶点坐标为
D.当 时, 随 的增大而增大
若将抛物线 先向左平移 个单位,再向下平移 个单位,得到新的抛物线,则新抛物线的表达式是
A. B.
C. D.
若抛物线 与 轴没有交点,则 的取值范围是
A. B. C. D.
把二次函数 化为 的形式,正确的是
A. B.
C. D.
如果在二次函数的表达式 中,,,,那么这个二次函数的图象可能是
A. B.
C. D.
若抛物线 经过点 ,则 的值是
A. B. C. D.
某一型号飞机着陆后滑行的距离 (单位:米)关于滑行的时间 (单位:秒)之间的函数解析式是 ,则该型号飞机着陆后滑行 秒才能停下来.
A. B. C. D.
已知二次函数 ( 为常数),当自变量 的值满足 时,与其对应的函数值 的最大值为 ,则 的值为
A. 或 B. 或 C. 或 D. 或
如图,在平面直角坐标系中,抛物线 经过平移得到抛物线 ,其对称轴与两段抛物线所围成的阴影部分的面积为
A. B. C. D.
二、填空题
二次函数 的最小值为 .
小明推铅球,铅球行进高度 与水平距离 之间的关系为 ,则小明推铅球的成绩是 .
抛物线 与 轴有 个交点.
下图是抛物线型拱桥,当拱顶离水面 时,水面宽 ,水面下降 ,水面宽度增
加 .
体育公园的圆形喷水池的中央竖直安装了一个柱形喷水装置 , 处为喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下(如图 ).如果曲线 表示的是落点 离点 最远的一条水流(如图 ),水流喷出的高度 (米)与水平距离 (米)之间的关系式是 ,那么圆形水池的半径至少为 米时,才能使喷出的水流不至于落在池外.
已知抛物线 (, 是常数)与 轴的公共点的坐标为 ,,且 ,则 与 的大小关系是 .
二次函数 的图象与 轴交于 两点(点 在点 的左侧),与 轴交于点 ,作直线 ,将直线 下方的二次函数图象沿直线 向上翻折,与其它剩余部分组成一个组合图象 ,若线段 与组合图象 有两个交点,则 的取值范围为 .
已知二次函数 的图象如图所示,并且关于 的一元二次方程 有两个不相等的实数根,下列结论:
① ;② ;③ ;④ .其中正确结论的有 (填序号).
三、解答题
已知二次函数 ,当 时有最大值,且函数的图象过点 .
(1) 求二次函数的解析式;
(2) 当 为何值时, 随 的增大而增大?
已知函数 ( 是常数).
(1) 求证:不论 为何值,该函数的图象都经过 轴上的一个定点;
(2) 若该函数的图象与 轴只有一个交点,求 的值.
已知二次函数 的图象经过 , 两点.
(1) 求 的值;
(2) 当 时,该函数的图象的顶点的纵坐标的最小值是 ;
(3) 设 是该函数的图象与 轴的一个公共点.当 时,结合函数的图象,直接写出 的取值范围.
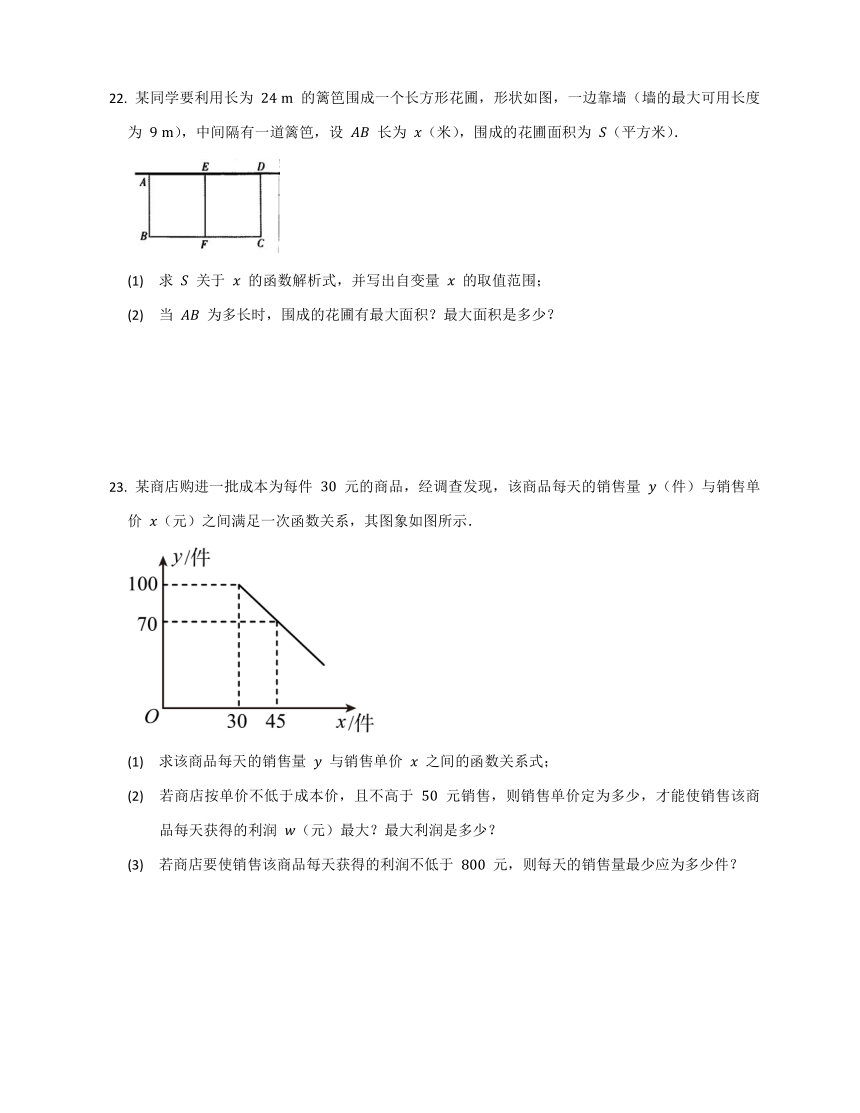
某同学要利用长为 的篱笆围成一个长方形花圃,形状如图,一边靠墙(墙的最大可用长度为 ),中间隔有一道篱笆,设 长为 (米),围成的花圃面积为 (平方米).
(1) 求 关于 的函数解析式,并写出自变量 的取值范围;
(2) 当 为多长时,围成的花圃有最大面积?最大面积是多少?
某商店购进一批成本为每件 元的商品,经调查发现,该商品每天的销售量 (件)与销售单价 (元)之间满足一次函数关系,其图象如图所示.
(1) 求该商品每天的销售量 与销售单价 之间的函数关系式;
(2) 若商店按单价不低于成本价,且不高于 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 (元)最大?最大利润是多少?
(3) 若商店要使销售该商品每天获得的利润不低于 元,则每天的销售量最少应为多少件?
如图,已知二次函数 的图象过 , 和 三点.
(1) 求这个二次函数的表达式.
(2) 设二次函数的图象与 轴的另一个交点为 ,求点 的坐标.
(3) 在同一平面直角坐标系中画出一次函数 的图象,写出当 在什么范围内时,一次函数的值大于二次函数的值.
年北京冬奥会的即将召开,激起了人们对冰雪运动的极大热情.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为 轴,过跳台终点 作水平线的垂线为 轴,建立平面直角坐标系,图中的抛物线 近似表示滑雪场地上的一座小山坡,某运动员从点 正上方 处的点 滑出,滑出后沿一段抛物线 运动.
(1) 当运动员滑出到离 处的水平距离为 时,离水平线的高度为 ,求抛物线 对应的函数表达式(不要求写出自变量 的取值范围).
(2) 在()的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为 ?
(3) 若运动员运动到坡顶正上方时,与坡顶距离超过 ,求 的取值范围.
答案
一、选择题
1. D
2. B
3. A
4. A
5. B
6. C
7. B
8. D
9. D
10. B
二、填空题
11.
12.
13.
14.
15.
16.
17. 或
18. ③
三、解答题
19.
(1) 依题意可得 ,把 代入,得 .解得 .
二次函数的解析式为 .
(2) 抛物线的对称轴为直线 ,抛物线开口向下,
当 时, 随 的增大而增大.
20.
(1) 当 时,.不论 为何值,函数 的图象经过 轴上的一个定点 .
(2) ①当 时,
函数 的图象与 轴只有一个交点;
②当 时,
函数 的图象与 轴只有一个交点,
则方程 有两个相等的实数根,
所以 ,.
综上所述,若函数 的图象与 轴只有一个交点,则 的值为 或 .
21.
(1) 把 , 代入 中,
得
两式相减得 ,
.
(2)
(3) 或 .
22.
(1) 由题意可知:,,即 ,解得 ,
.
(2) 由()可知 ,
,,
当 时, 有最大值,(平方米),
即当 米时,围成的花圃有最大面积,最大面积是 平方米.
23.
(1)
(2) 销售单价定为 元时, 有最大值为 元
(3) 最少应为 件
24.
(1) .
(2) 当 时,得 .
解得 ,.
点 的坐标为 .
(3) 图象如图,
当一次函数的值大于二次函数的值时, 的取值范围是 .
25.
(1) 由题意,得抛物钱 过点 和 ,将其代入,得
解得
抛物钱 对应的函数表达式为 .
(2) 设运动员运动的水平距离为 时,运动员与小山坡的竖直距离为 .
由题意,,
即 ,解得 ,(不合题意,舍去).
当运动员运动的水平距离为 时,运动员与小山坡的竖直距离为 .
(3) ,
当 时,运动员到达坡顶正上方.
由题意,得 ,
解得 .
一、选择题
下列函数是二次函数的是
A. B.
C. D.
由二次函数 可知
A.其图象的开口向下
B.其图象的对称轴为直线
C.其顶点坐标为
D.当 时, 随 的增大而增大
若将抛物线 先向左平移 个单位,再向下平移 个单位,得到新的抛物线,则新抛物线的表达式是
A. B.
C. D.
若抛物线 与 轴没有交点,则 的取值范围是
A. B. C. D.
把二次函数 化为 的形式,正确的是
A. B.
C. D.
如果在二次函数的表达式 中,,,,那么这个二次函数的图象可能是
A. B.
C. D.
若抛物线 经过点 ,则 的值是
A. B. C. D.
某一型号飞机着陆后滑行的距离 (单位:米)关于滑行的时间 (单位:秒)之间的函数解析式是 ,则该型号飞机着陆后滑行 秒才能停下来.
A. B. C. D.
已知二次函数 ( 为常数),当自变量 的值满足 时,与其对应的函数值 的最大值为 ,则 的值为
A. 或 B. 或 C. 或 D. 或
如图,在平面直角坐标系中,抛物线 经过平移得到抛物线 ,其对称轴与两段抛物线所围成的阴影部分的面积为
A. B. C. D.
二、填空题
二次函数 的最小值为 .
小明推铅球,铅球行进高度 与水平距离 之间的关系为 ,则小明推铅球的成绩是 .
抛物线 与 轴有 个交点.
下图是抛物线型拱桥,当拱顶离水面 时,水面宽 ,水面下降 ,水面宽度增
加 .
体育公园的圆形喷水池的中央竖直安装了一个柱形喷水装置 , 处为喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下(如图 ).如果曲线 表示的是落点 离点 最远的一条水流(如图 ),水流喷出的高度 (米)与水平距离 (米)之间的关系式是 ,那么圆形水池的半径至少为 米时,才能使喷出的水流不至于落在池外.
已知抛物线 (, 是常数)与 轴的公共点的坐标为 ,,且 ,则 与 的大小关系是 .
二次函数 的图象与 轴交于 两点(点 在点 的左侧),与 轴交于点 ,作直线 ,将直线 下方的二次函数图象沿直线 向上翻折,与其它剩余部分组成一个组合图象 ,若线段 与组合图象 有两个交点,则 的取值范围为 .
已知二次函数 的图象如图所示,并且关于 的一元二次方程 有两个不相等的实数根,下列结论:
① ;② ;③ ;④ .其中正确结论的有 (填序号).
三、解答题
已知二次函数 ,当 时有最大值,且函数的图象过点 .
(1) 求二次函数的解析式;
(2) 当 为何值时, 随 的增大而增大?
已知函数 ( 是常数).
(1) 求证:不论 为何值,该函数的图象都经过 轴上的一个定点;
(2) 若该函数的图象与 轴只有一个交点,求 的值.
已知二次函数 的图象经过 , 两点.
(1) 求 的值;
(2) 当 时,该函数的图象的顶点的纵坐标的最小值是 ;
(3) 设 是该函数的图象与 轴的一个公共点.当 时,结合函数的图象,直接写出 的取值范围.
某同学要利用长为 的篱笆围成一个长方形花圃,形状如图,一边靠墙(墙的最大可用长度为 ),中间隔有一道篱笆,设 长为 (米),围成的花圃面积为 (平方米).
(1) 求 关于 的函数解析式,并写出自变量 的取值范围;
(2) 当 为多长时,围成的花圃有最大面积?最大面积是多少?
某商店购进一批成本为每件 元的商品,经调查发现,该商品每天的销售量 (件)与销售单价 (元)之间满足一次函数关系,其图象如图所示.
(1) 求该商品每天的销售量 与销售单价 之间的函数关系式;
(2) 若商店按单价不低于成本价,且不高于 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 (元)最大?最大利润是多少?
(3) 若商店要使销售该商品每天获得的利润不低于 元,则每天的销售量最少应为多少件?
如图,已知二次函数 的图象过 , 和 三点.
(1) 求这个二次函数的表达式.
(2) 设二次函数的图象与 轴的另一个交点为 ,求点 的坐标.
(3) 在同一平面直角坐标系中画出一次函数 的图象,写出当 在什么范围内时,一次函数的值大于二次函数的值.
年北京冬奥会的即将召开,激起了人们对冰雪运动的极大热情.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为 轴,过跳台终点 作水平线的垂线为 轴,建立平面直角坐标系,图中的抛物线 近似表示滑雪场地上的一座小山坡,某运动员从点 正上方 处的点 滑出,滑出后沿一段抛物线 运动.
(1) 当运动员滑出到离 处的水平距离为 时,离水平线的高度为 ,求抛物线 对应的函数表达式(不要求写出自变量 的取值范围).
(2) 在()的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为 ?
(3) 若运动员运动到坡顶正上方时,与坡顶距离超过 ,求 的取值范围.
答案
一、选择题
1. D
2. B
3. A
4. A
5. B
6. C
7. B
8. D
9. D
10. B
二、填空题
11.
12.
13.
14.
15.
16.
17. 或
18. ③
三、解答题
19.
(1) 依题意可得 ,把 代入,得 .解得 .
二次函数的解析式为 .
(2) 抛物线的对称轴为直线 ,抛物线开口向下,
当 时, 随 的增大而增大.
20.
(1) 当 时,.不论 为何值,函数 的图象经过 轴上的一个定点 .
(2) ①当 时,
函数 的图象与 轴只有一个交点;
②当 时,
函数 的图象与 轴只有一个交点,
则方程 有两个相等的实数根,
所以 ,.
综上所述,若函数 的图象与 轴只有一个交点,则 的值为 或 .
21.
(1) 把 , 代入 中,
得
两式相减得 ,
.
(2)
(3) 或 .
22.
(1) 由题意可知:,,即 ,解得 ,
.
(2) 由()可知 ,
,,
当 时, 有最大值,(平方米),
即当 米时,围成的花圃有最大面积,最大面积是 平方米.
23.
(1)
(2) 销售单价定为 元时, 有最大值为 元
(3) 最少应为 件
24.
(1) .
(2) 当 时,得 .
解得 ,.
点 的坐标为 .
(3) 图象如图,
当一次函数的值大于二次函数的值时, 的取值范围是 .
25.
(1) 由题意,得抛物钱 过点 和 ,将其代入,得
解得
抛物钱 对应的函数表达式为 .
(2) 设运动员运动的水平距离为 时,运动员与小山坡的竖直距离为 .
由题意,,
即 ,解得 ,(不合题意,舍去).
当运动员运动的水平距离为 时,运动员与小山坡的竖直距离为 .
(3) ,
当 时,运动员到达坡顶正上方.
由题意,得 ,
解得 .
同课章节目录
