人教版八年级数学上名师点拨精练第12章全等三角形12.1全等三角形
文档属性
| 名称 | 人教版八年级数学上名师点拨精练第12章全等三角形12.1全等三角形 |

|
|
| 格式 | doc | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-07 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.1全等三角形
学习目标
1.了解全等形和全等三角形的概念.
2.能够找出全等三角形的对应元素.
3.掌握全等三角形的对应边、角相等.
【重点】探究全等三角形的性质.
【难点】掌握两个全等三角形的对应边、对应角的寻找规律,迅速正确地指出两个全等三角形的对应元素.
老师告诉你
全等三角形的性质的作用:
1.求角的度数
2.证明两个角相等
3.求线段的长度
4.证明两条线段相等
5.判断两条直线的位置关系
知识点拨
知识点1 全等图形
形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.
在平面几何中,一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.两个全等形的周长相等,面积相等.
【新知导学】
例1-1.如图所示的各组图形中,不是全等形的是( )
A. B.
C. D.
【对应导练】
1.下列图形中被虚线分成的两部分不是全等形的是( )
A. B.
C. D.
2.下列图标中,不是由全等图形组合成的是( )
A. B.
C. D.
3.下列说法正确的是( )
A. 两个面积相等的图形一定是全等图形
B. 两个正方形是全等图形
C. 若两个图形的周长相等,则它们一定是全等图形
D. 两个全等图形的面积一定相等
4.请观察图中的5组图案,其中是全等形的是_____(填序号).
知识点2 全等三角形及其对应元素
1.全等三角形:能够完全重合的两个三角形叫全等三角形.
2.对应边、对应角、对应顶点的定义:
两个全等三角形重合在一起,重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.
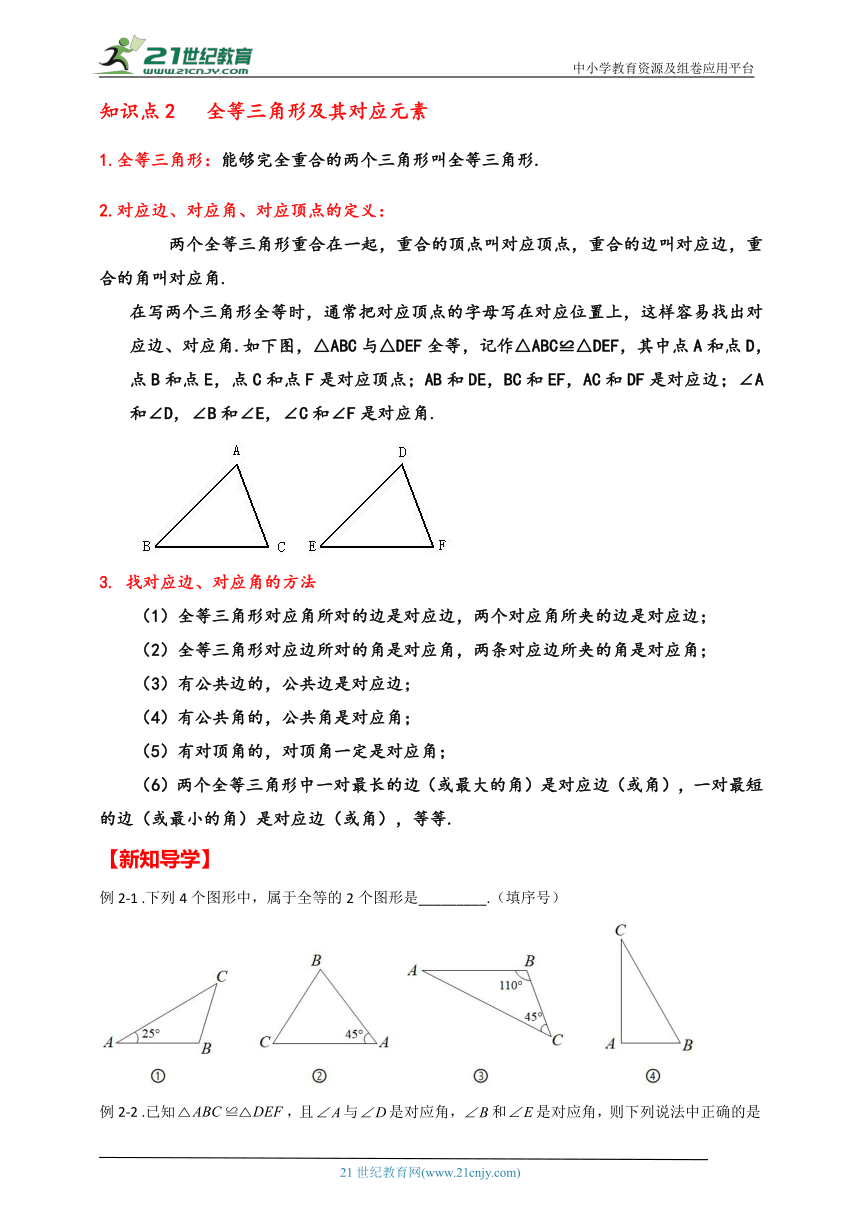
在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角.如下图,△ABC与△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.
3. 找对应边、对应角的方法
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
(3)有公共边的,公共边是对应边;
(4)有公共角的,公共角是对应角;
(5)有对顶角的,对顶角一定是对应角;
(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角),等等.
【新知导学】
例2-1 .下列4个图形中,属于全等的2个图形是_________.(填序号)
例2-2 .已知,且与是对应角,和是对应角,则下列说法中正确的是( )
A.与是对应边 B.与是对应边
C.与是对应边 D.不能确定 的对应边
【对应导练】
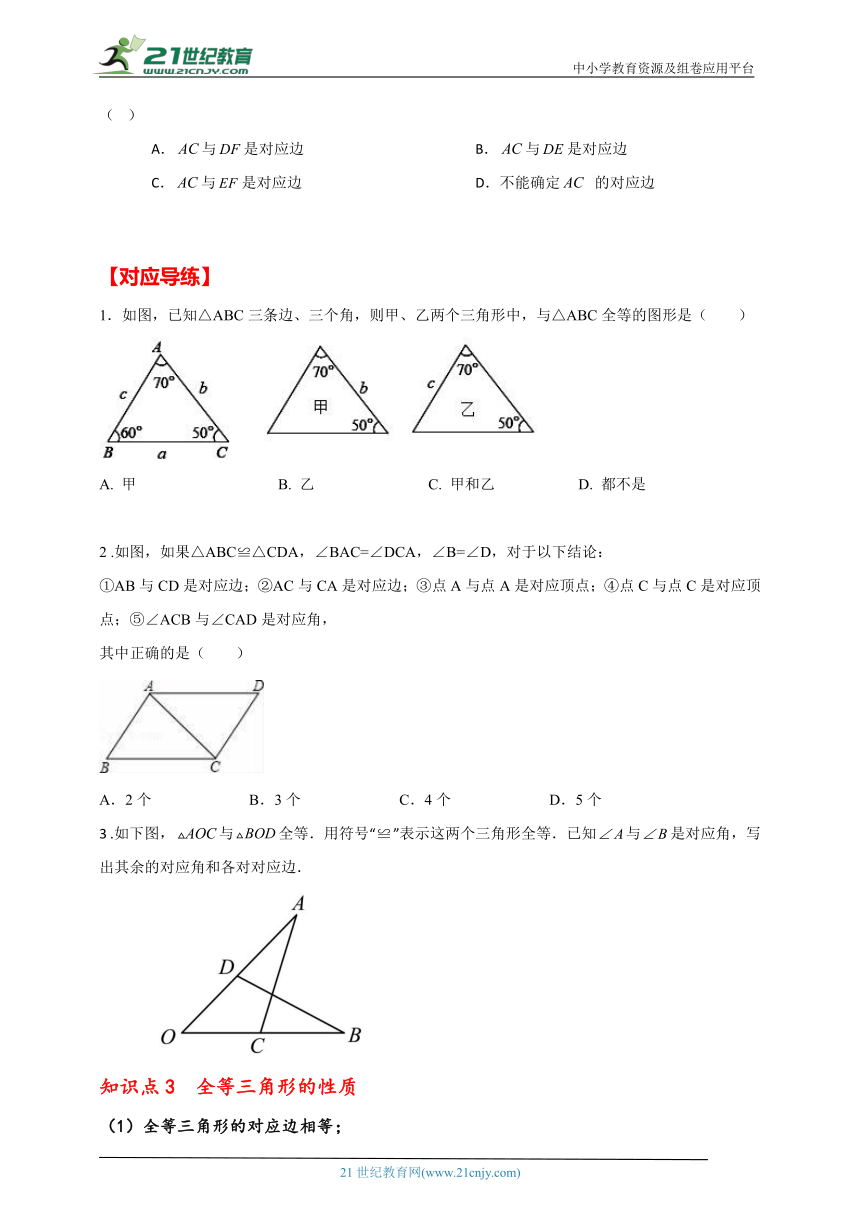
1.如图,已知△ABC三条边、三个角,则甲、乙两个三角形中,与△ABC全等的图形是( )
A. 甲 B. 乙 C. 甲和乙 D. 都不是
2 .如图,如果△ABC≌△CDA,∠BAC=∠DCA,∠B=∠D,对于以下结论:
①AB与CD是对应边;②AC与CA是对应边;③点A与点A是对应顶点;④点C与点C是对应顶点;⑤∠ACB与∠CAD是对应角,
其中正确的是( )
A.2个 B.3个 C.4个 D.5个
3 .如下图,与全等.用符号“”表示这两个三角形全等.已知与是对应角,写出其余的对应角和各对对应边.
知识点3 全等三角形的性质
(1)全等三角形的对应边相等;
(2)全等三角形的对应角相等;
后面还会学到:全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.
【新知导学】
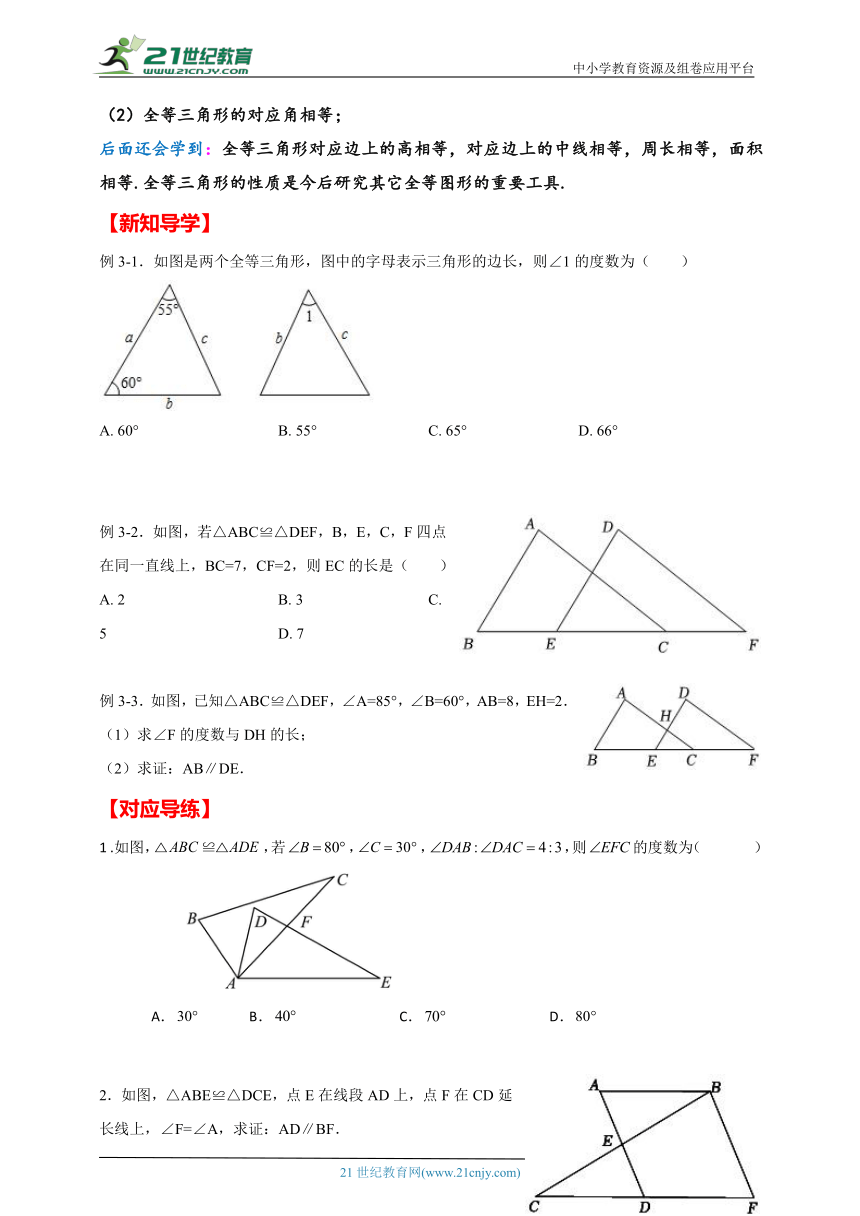
例3-1.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数为( )
A. 60° B. 55° C. 65° D. 66°
例3-2.如图,若△ABC≌△DEF,B,E,C,F四点在同一直线上,BC=7,CF=2,则EC的长是( )
A. 2 B. 3 C. 5 D. 7
例3-3.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求∠F的度数与DH的长;
(2)求证:AB∥DE.
【对应导练】
1 .如图,,若,,,则的度数为( )
A. B. C. D.
2.如图,△ABE≌△DCE,点E在线段AD上,点F在CD延长线上,∠F=∠A,求证:AD∥BF.
3.已知,如图∠B=90°,△ABC≌△CDE,B、C、D三点共线.试说明:AC⊥CE.
4.如图,△ABC≌△ADE,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:∠CAE=∠BAD;
(2)若∠BAD=35°,求∠BED的度数.
题型训练
利用全等三角形性质判断两直线的位置
1.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
2.如图,A,D,E三点在同一直线上,且△BAD≌△ACE,试说明:
(1)BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE.
.利用全等三角形求角度
3.如图,△ABC≌△ADE,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:∠CAE=∠BAD;
(2)若∠BAD=35°,求∠BED的度数.
4.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
利用全等三角形求周长
5 .如图,△ACF≌△ADE,AD=12,AE=5,求DF的长.
6.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.
利用全等三角形判断图形形状
7 .如图,D、A、E三点在同一条直线上,BD⊥DE于点D,CE⊥DE于点E,且△ABD≌△CAE,AC=4.
(1)求∠BAC的度数;
(2)判断△ABC的形状,并求△ABC的面积.
牛刀小试
一、单选题(每小题4分,共32分)
1.下列图形中被虚线分成的两部分不是全等形的是( )
A. B.
C. D.
2.下图中全等的三角形是( )
A.①和② B.②和④ C.②和③ D.①和③
3.如图,,且,,则的度数的值为( )
A. B. C. D.
4.如图,,,,则的长度为( )
A. B. C. D.
5.如图,若,则下列结论中一定成立的是( )
A. B. C. D.
6.2.下列图形中是全等形的是( )
A. B.
C. D.
7.如图,点B,E,C,F在同一直线上,,,,则EC的长为( )
A.5 B.4.5 C.4 D.3.5
8.三个全等三角形按如图的形式摆放,则的度数是( )
A. B. C. D.
二、填空题(每小题4分,共20分)
9.已知,且的周长为6,若,则DF的长为_________.
10.如图,D在边上,,,则的度数为______.
11.如图,四边形四边形,若,,,则____________°.
12.如图,在平面直角坐标系中,,则点D的坐标是__________.
13.如图,在正方形中,,延长到点E,使,连接,动点P从点A出发,以每秒的速度沿向终点A运动.设点P的运动时间为t秒,当和全等时,t的值为_____.
三、解答题(共6小题,共48分)
14.(8分)试在下列图形中,沿正方形的网格线(虚线)画线,将图形分割成两个全等的图形.
15.(8分)如图,A,C,E三点在同一直线上,且.
(1)求证:.
(2)若,求证:.
16.(8分)如图,在中,cm,cm,D为AB的中点,点P在线段BC上以3cm/s的速度由点B向点C运动,同时点Q在线段CA上由点C向点A以a cm/s的速度运动,设运动的时间为t s.
(1)求CP的长度(用含t的代数式表示);
(2)若以点C,P,Q为顶点的三角形和以点B,D,P为顶点的三角形全等,且和是对应角,求a的值.
17.(8分)如图,,其中点A,B,C,D在一条直线上.
(1)若,,求的度数;
(2)若cm,cm,求AB的长.
18.(8分)如图,已知,点D在上,与交于点P.
(1)若,,求的 度数.
(2)若,,求与的周长之和.
19.如图,试说明:
(1)
(2)
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.1全等三角形
学习目标
1.了解全等形和全等三角形的概念.
2.能够找出全等三角形的对应元素.
3.掌握全等三角形的对应边、角相等.
【重点】探究全等三角形的性质.
【难点】掌握两个全等三角形的对应边、对应角的寻找规律,迅速正确地指出两个全等三角形的对应元素.
老师告诉你
全等三角形的性质的作用:
1.求角的度数
2.证明两个角相等
3.求线段的长度
4.证明两条线段相等
5.判断两条直线的位置关系
知识点拨
知识点1 全等图形
形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.
在平面几何中,一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.两个全等形的周长相等,面积相等.
【新知导学】
例1-1.如图所示的各组图形中,不是全等形的是( )
A. B.
C. D.
【答案】B
【解析】根据能够完全重合的两个图形是全等图形对各选项分析即可得解.
解:观察发现,A、C、D选项的两个图形都可以完全重合,是全等图形,
B选项中圆与椭圆不可能完全重合,不是全等形.
故选:B.
【对应导练】
1.下列图形中被虚线分成的两部分不是全等形的是( )
A. B.
C. D.
【答案】C
【解析】根据全等形的概念进行判断即可.
解:A、长方形被对角线分成的两部分是全等形;
B、正六边形被对角线分成的两部分是全等形;
C、梯形被对角线分成的两部分不是全等形;
D、圆被对角线分成的两部分是全等形,
故选:C.
2.下列图标中,不是由全等图形组合成的是( )
A. B.
C. D.
【答案】C
【解析】根据全等图形的概念分析即可.
解:A、该图象是由三个全等的图形构成,故该选项不符合题意;
B、该图象是由五个全等的图形构成,故该选项不符合题意;
C、该图象不是由全等图形构成,故该选项符合题意;
D、该图象是由两个全等的图形构成,故该选项不符合题意;
故选:C.
3.下列说法正确的是( )
A. 两个面积相等的图形一定是全等图形
B. 两个正方形是全等图形
C. 若两个图形的周长相等,则它们一定是全等图形
D. 两个全等图形的面积一定相等
【答案】D
【解析】依据全等图形的定义和性质进行判断即可.
解:A、两个面积相等的图形不一定是全等图形,说法错误,不符合题意;
B、两个边长相等的正方形是全等图形,说法错误,不符合题意;
C、若两个图形的周长相等,则它们不一定是全等图形,说法错误,不符合题意;
D、两个全等图形的面积一定相等,说法正确,符合题意;
故选:D.
4.请观察图中的5组图案,其中是全等形的是_____(填序号).
【答案】(1)(4)(5)
【解析】能够完全重合的两个图形叫做全等形,结合所给图形进行判断即可.
解:5组图案,其中是全等形的是(1)(4)(5).
故答案为:是(1)(4)(5).
知识点2 全等三角形及其对应元素
1.全等三角形:能够完全重合的两个三角形叫全等三角形.
2.对应边、对应角、对应顶点的定义:
两个全等三角形重合在一起,重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.
在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角.如下图,△ABC与△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.
3. 找对应边、对应角的方法
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
(3)有公共边的,公共边是对应边;
(4)有公共角的,公共角是对应角;
(5)有对顶角的,对顶角一定是对应角;
(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角),等等.
【新知导学】
例2-1 .下列4个图形中,属于全等的2个图形是_________.(填序号)
【答案】①③
【分析】先求出的度数,然后分析求解即可.
【详解】解:在③中,,
∴与①中的相等,并且两夹边对应相等,
∴属于全等的2个图形是①③
故答案为①③.
【点评】本题考查了三角形全等的条件,熟悉全等三角形的判定定理是解题的关键.
例2-2 .已知,且与是对应角,和是对应角,则下列说法中正确的是( )
A.与是对应边 B.与是对应边
C.与是对应边 D.不能确定 的对应边
【答案】A
【分析】根据全等三角形的概念即可得到答案.
解:与是对应角,和是对应角,
和是对应角,
与是对应边,
故选A.
【点拨】本题考查了全等三角形,理解全等三角形的概念,准确找出对应边是解题关键.
【对应导练】
1.如图,已知△ABC三条边、三个角,则甲、乙两个三角形中,与△ABC全等的图形是( )
A. 甲 B. 乙 C. 甲和乙 D. 都不是
【答案】C
【解析】甲可根据ASA判定与△ABC全等;乙可根据AAS判定与△ABC全等,可得答案.
解:甲三角形夹b边的两角分别与已知三角形对应相等,故甲与△ABC全等;
乙三角形50°内角及所对边与△ABC对应相等且均有70°内角,可根据AAS判定乙与△ABC全等;
则与△ABC全等的有乙和甲,
故选:C.
2 .如图,如果△ABC≌△CDA,∠BAC=∠DCA,∠B=∠D,对于以下结论:
①AB与CD是对应边;②AC与CA是对应边;③点A与点A是对应顶点;④点C与点C是对应顶点;⑤∠ACB与∠CAD是对应角,
其中正确的是( )
A.2个 B.3个 C.4个 D.5个
【答案】B
【分析】由全等三角形的对应边相等、对应角相等对以下结论进行判定.
【详解】解:△ABC≌△CDA,∠BAC=∠DCA,∠B=∠D.
①AB与CD是对应边.故①正确;
②AC与CA是对应边.故②正确;
③点A与点C是对应顶点.故③错误;
④点C与点A是对应顶点.故④错误;
⑤∠ACB与∠CAD是对应角.故⑤正确.
综上所述,正确的结论是①②⑤,共有3个.
故选B.
3 .如下图,与全等.用符号“”表示这两个三角形全等.已知与是对应角,写出其余的对应角和各对对应边.
【答案】.对应角是:与,与;
对应边是;OA与OB,OC与OD,AC与BD.
【分析】根据全等三角形的表示法以及全等三角形的性质即可得到答案.
解: .
因为与是对应角,所以其余的对应角是:
与,与;
对应边是;OA与OB,OC与OD,AC与BD.
【点拨】本题主要考查全等三角形的表示法和性质,准确找到全等三角形的对应角和对应边是关键.
知识点3 全等三角形的性质
(1)全等三角形的对应边相等;
(2)全等三角形的对应角相等;
后面还会学到:全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.
【新知导学】
例3-1.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数为( )
A. 60° B. 55° C. 65° D. 66°
【答案】C
【解析】直接利用全等三角形的性质得出∠1=∠2进而得出答案.
解:∵如图是两个全等三角形,
∴∠1=∠2=180°-60°-55°=65°.
故选:C.
例3-2.如图,若△ABC≌△DEF,B,E,C,F四点在同一直线上,BC=7,CF=2,则EC的长是( )
A. 2 B. 3 C. 5 D. 7
【答案】C
【解析】利用全等三角形的性质可得BC=EF=7,再利用线段的和差关系计算即可.
解:∵△ABC≌△DEF,
∴BC=EF=7,
∴CF=2,
∴EC=EF-CF=7-2=5,
故选:C.
例3-3.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求∠F的度数与DH的长;
(2)求证:AB∥DE.
【解析】(1)根据三角形内角和定理求出∠ACB,根据全等三角形的性质得出AB=DE,∠F=∠ACB,即可得出答案;
(2)根据全等三角形的性质得出∠B=∠DEF,根据平行线的判定得出即可.
解:(1)∵∠A=85°,∠B=60°,
∴∠ACB=180°-∠A-∠B=35°,
∵△ABC≌△DEF,AB=8,
∴∠F=∠ACB=35°,DE=AB=8,
∵EH=2,
∴DH=8-2=6;
(2)证明:∵△ABC≌△DEF,
∴∠DEF=∠B,
∴AB∥DE.
【对应导练】
1 .如图,,若,,,则的度数为( )
A. B. C. D.
【答案】C
【分析】首先根据三角形内角和定理求出,然后根据全等三角形的性质得到,,最后利用三角形外角的性质求解即可.
解:∵,,
∴
∵
∴
∵
∴,
∴
∴.
故选:C.
【点拨】本题考查了全等三角形的性质和三角形内角和定理的应用,三角形外角的性质,解题的关键是掌握以上知识点,全等三角形的对应角相等,对应边相等.
2.如图,△ABE≌△DCE,点E在线段AD上,点F在CD延长线上,∠F=∠A,求证:AD∥BF.
【解析】根据△ABE≌△DCE得到∠A=∠ADC,然后利用∠F=∠A得到∠F=∠EDC,利用同位角相等,两直线平行证得结论.
证明:∵△ABE≌△DCE,
∴∠A=∠ADC,
∵∠F=∠A,
∴∠F=∠EDC,
∴AD∥BF.
3.已知,如图∠B=90°,△ABC≌△CDE,B、C、D三点共线.试说明:AC⊥CE.
【解析】根据Rt△ABC≌Rt△CDE可得∠BCA=∠CED,再根据直角三角形两锐角互余可得∠CED+∠ECD=90°,进而得到∠BCA+∠ECD=90°,再根据角之间的关系可得∠ACE=90°.
证明:∵∠B=90°,△ABC≌△CDE,
∴∠D=90°,
∴∠BCA=∠CED,
∵△DCE是直角三角形,
∴∠CED+∠ECD=90°,
∴∠BCA+∠ECD=90°,
∴∠ACE=180°-90°=90°,
∴AC⊥CE.
4.如图,△ABC≌△ADE,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:∠CAE=∠BAD;
(2)若∠BAD=35°,求∠BED的度数.
【解析】(1)根据全等三角形的性质得出∠BAC=∠DAE,再求出答案即可;
(2)根据全等三角形的性质得出∠D=∠B,根据对顶角相等和三角形内角和定理得出∠AFD=∠EFB,∠D+∠BAD+∠AFD=180°,∠B+∠EFB+∠BED=180°,求出∠BED=∠BAD即可.
(1)证明:∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC-∠BAE=∠DAE-∠BAE,
∴∠CAE=∠BAD;
(2)解:∵△ABC≌△ADE,
∴∠D=∠B,
∵∠AFD=∠EFB,∠D+∠BAD+∠AFD=180°,∠B+∠EFB+∠BED=180°,
∴∠BED=∠BAD,
∵∠BAD=35°,
∴∠BED=35°.
题型训练
利用全等三角形性质判断两直线的位置
1.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
【解析】(1)根据平行线性质求出∠A=∠B,根据SAS推出即可.
(2)根据全等三角形性质推出CD=CE,根据等腰三角形性质求出即可.
证明:(1)∵AD∥BE,
∴∠A=∠B,
在△ACD和△BEC中
∴△ACD≌△BEC(SAS),
(2)∵△ACD≌△BEC,
∴CD=CE,
又∵CF平分∠DCE,
∴CF⊥DE.
2.如图,A,D,E三点在同一直线上,且△BAD≌△ACE,试说明:
(1)BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE.
【答案】(1)证明见解析;(2)∠ADB=90°.
【分析】(1)根据全等三角形的性质求出BD=AE,AD=CE,代入求出即可;
(2)根据全等三角形的性质求出∠E=∠BDA=90°,推出∠BDE=90°,根据平行线的判定求出即可.
【详解】解:(1)∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE;
(2)△ABD满足∠ADB=90°时,BD∥CE,
理由是:∵△BAD≌△ACE,
∴∠E=∠ADB=90°,
∴∠BDE=180° 90°=90°=∠E,
∴BD∥CE.
【点评】本题考查了全等三角形的性质和平行线的判定等的应用,关键是通过三角形全等得出正确的结论,通过做此题培养了学生分析问题的能力.
.利用全等三角形求角度
3.如图,△ABC≌△ADE,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:∠CAE=∠BAD;
(2)若∠BAD=35°,求∠BED的度数.
【解析】(1)根据全等三角形的性质得出∠BAC=∠DAE,再求出答案即可;
(2)根据全等三角形的性质得出∠D=∠B,根据对顶角相等和三角形内角和定理得出∠AFD=∠EFB,∠D+∠BAD+∠AFD=180°,∠B+∠EFB+∠BED=180°,求出∠BED=∠BAD即可.
(1)证明:∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC-∠BAE=∠DAE-∠BAE,
∴∠CAE=∠BAD;
(2)解:∵△ABC≌△ADE,
∴∠D=∠B,
∵∠AFD=∠EFB,∠D+∠BAD+∠AFD=180°,∠B+∠EFB+∠BED=180°,
∴∠BED=∠BAD,
∵∠BAD=35°,
∴∠BED=35°.
4.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
【解析】(1)根据全等三角形的性质得到AB=DE=10,BE=BC=4,结合图形计算,得到答案;
(2)根据全等三角形的性质得到∠BAC=∠D=30°,∠DBE=∠C=70°,根据三角形内角和定理求出∠ABC,计算即可.
解:(1)∵△ABC≌△DEB,DE=10,BC=4,
∴AB=DE=10,BE=BC=4,
∴AE=AB-BE=6;
(2)∵△ABC≌△DEB,∠D=30°,∠C=70°,
∴∠BAC=∠D=30°,∠DBE=∠C=70°,
∴∠ABC=180°-30°-70°=80°,
∴∠DBC=∠ABC-∠DBE=10°.
利用全等三角形求周长
5 .如图,△ACF≌△ADE,AD=12,AE=5,求DF的长.
【解析】直接利用全等三角形的性质得出AC=AD,进而得出答案.
解:∵△ACF≌△ADE,AD=12,AE=5,
∴AC=AD=12,AE=AF=5,
∴DF=12-5=7.
6.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.
【解析】(1)根据全等三角形的性质得到∠ABC=∠DBE,计算即可;
(2)根据全等三角形的性质求出BE、DE,根据三角形的周长公式计算即可.
解:(1)∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,
∴∠ABD=∠CBE=132°÷2=66°,
即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,
∴DE=AC=AD+DC=5,BE=BC=4,
∴△CDP与△BEP的周长和=DC+DP+PC+BP+PE+BE=DC+DE+BC+BE=2.5+5+4+4=15.5.
利用全等三角形判断图形形状
7 .如图,D、A、E三点在同一条直线上,BD⊥DE于点D,CE⊥DE于点E,且△ABD≌△CAE,AC=4.
(1)求∠BAC的度数;
(2)判断△ABC的形状,并求△ABC的面积.
【答案】(1)90°
等腰直角三角形,8
【分析】(1)根据垂直的定义得到∠D=90°,求得∠DBA+∠BAD=90°,根据全等三角形的性质得到∠DBA=∠CAE,等量代换即可得到结论;
(2)根据全等三角形的性质得AC=AB=4,再根据三角形的面积求出答案.
【详解】(1)解:∵BD⊥DE,
∴∠D=90°,
∴∠DBA+∠BAD=90°,
∵△ABD≌△CAE,
∴∠DBA=∠CAE
∴∠BAD+∠CAE=90°,
∴∠BAC=90°;
(2)解:∵△ABD≌△CAE,
∴AC=AB=4,
又∵∠BAC=90°
∴△ABC是等腰直角三角形,
∴△ABC的面积=4×4÷2=8.
【点评】本题考查的是全等三角形的性质、三角形的面积公式,证得△ABC是直角三角形是解决本题的关键.
牛刀小试
一、单选题(每小题4分,共32分)
1.下列图形中被虚线分成的两部分不是全等形的是( )
A. B.
C. D.
【答案】:A
解析:观察选项可知,选项B,C,D中的虚线把图形分成全等的两部分,
故选:A.
【点评】此题主要考查了全等图形,关键是掌握能够完全重合的两个图形叫做全等形.
2.下图中全等的三角形是( )
A.①和② B.②和④ C.②和③ D.①和③
【答案】D
解析:A、①和②,SA,角的另一条邻边不相等,两个三角形不全等,不符合题意;
B、②和④,5cm分别是图②和图④30°的邻边和对边,两个三角形不全等,不符合题意;
C、②和③,SA,角的另一条邻边不相等,两个三角形不全等,不符合题意;
D、①和③,SAS,两个三角形全等,符合题意;
故选D.
【点拨】本题考查了全等三角形,理解全等三角形的概念,准确找出对应边是解题关键.
3.如图,,且,,则的度数的值为( )
A. B. C. D.
【答案】D
解析:,,
,,
,
,
,
.
故选:D.
【点拨】本题考查了全等三角形的性质和三角形内角和定理的应用,三角形外角的性质,解题的关键是掌握以上知识点,全等三角形的对应角相等,对应边相等.
4.如图,,,,则的长度为( )
A. B. C. D.
【答案】B
解析:,
,,
.
故选:B.
【点评】此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应边相等.
5.如图,若,则下列结论中一定成立的是( )
A. B. C. D.
【答案】:B
解析:,
,,,,
,
即.
故A,C,D选项错误,B选项正确,
故选:B.
【点拨】本题考查了全等三角形的性质,,结合图形和题意找到角之间的关系是解题的关键.
6.2.下列图形中是全等形的是( )
A. B.
C. D.
【答案】:D
解析:A.两个图形不能完全重合,不是全等形;
B.两个图形不能完全重合,不是全等形;
C.两个图形不能完全重合,不是全等形;
D.两个图形能完全重合,是全等形;
故选:D.
【点评】此题主要考查了全等图形,关键是掌握能够完全重合的两个图形叫做全等形.
7.如图,点B,E,C,F在同一直线上,,,,则EC的长为( )
A.5 B.4.5 C.4 D.3.5
【答案】:B
解析:,,
,
,,
,
,
故选:B.
【点评】此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应边相等.
8.三个全等三角形按如图的形式摆放,则的度数是( )
A. B. C. D.
【答案】D
解析:如图所示:
由图形可得:,
三个全等三角形,
,
又,
,
的度数是.
故选:D.
【点拨】本题考查了全等三角形的性质,三角形内角和,结合图形和题意找到角之间的关系是解题的关键.
二、填空题(每小题4分,共20分)
9.已知,且的周长为6,若,则DF的长为_________.
【答案】2.1
解析:,,
,
的周长为6,
,
故答案为:2.1.
【点评】此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应边相等。
10.如图,D在边上,,,则的度数为______.
【答案】
解析:,
,,
,,
中,,
,
故答案为:.
【点评】此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应角相等.
11.如图,四边形四边形,若,,,则____________°.
【答案】105
解析:四边形四边形,
,,
,
,
,,
,
,
故答案为:105.
【点评】本题主要考查了全等图形的定义,解题的关键是熟练掌握形状和大小都相同的图形是全等图形.
12.如图,在平面直角坐标系中,,则点D的坐标是__________.
【答案】
解析:,,点D的坐标是.
【点评】本题主要考查了坐标与图形,全等三角形的性质,掌握全等三角形性质是解题的关键.
13.如图,在正方形中,,延长到点E,使,连接,动点P从点A出发,以每秒的速度沿向终点A运动.设点P的运动时间为t秒,当和全等时,t的值为_____.
答案:2或7
解析:正方形ABCD,
,,
是直角三角形,
为直角三角形,
点P只能在上或者上,
当点P在上时,如图,当时,有,
,
,
,
当点P在上时,则当时,有,
,
故答案为:2或7.
【点评】本题考查了全等三角形的性质,明确全等三角形的对应角所对的边为对应边是解本题的关键.
三、解答题(共6小题,共48分)
14.(8分)试在下列图形中,沿正方形的网格线(虚线)画线,将图形分割成两个全等的图形.
答案:如图所示.
解析:
15.(8分)如图,A,C,E三点在同一直线上,且.
(1)求证:.
(2)若,求证:.
答案:(1)见解析
(2)见解析
解析:(1),
,,
,
;
(2),
,,
,
.
【点评】本题考查了全等三角形的性质和平行线的判定等的应用,关键是通过三角形全等得出正确的结论,通过做此题培养了学生分析问题的能力.
16.(8分)如图,在中,cm,cm,D为AB的中点,点P在线段BC上以3cm/s的速度由点B向点C运动,同时点Q在线段CA上由点C向点A以a cm/s的速度运动,设运动的时间为t s.
(1)求CP的长度(用含t的代数式表示);
(2)若以点C,P,Q为顶点的三角形和以点B,D,P为顶点的三角形全等,且和是对应角,求a的值.
答案:(1)因为cm,cm,
所以cm.
(2)①当时,因为,D为AB的中点,
所以,所以,解得.
此时,
所以,即,解得.
②当时,,解得.
此时,
所以,即,解得.
综上所述,a的值为3或.
【点评】本题主要考查了全等三角形的性质,利用分类讨论思想解答是解题的关键.
17.(8分)如图,,其中点A,B,C,D在一条直线上.
(1)若,,求的度数;
(2)若cm,cm,求AB的长.
答案:(1),.
,
,
.
(2),,
,即.
cm,cm,
(cm),
cm.
【点评】此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应边相等;全等三角形的对应角相等.
18.(8分)如图,已知,点D在上,与交于点P.
(1)若,,求的 度数.
(2)若,,求与的周长之和.
答案:(1),
,
即,
(2),
,
【点拨】本题考查全等三角形的性质,掌握全等三角形的性质是解题的关键.
19.如图,试说明:
(1)
(2)
答案:(1)
(2)时,
理由如下: (添加的条件是)
【点评】本题主要考查了全等三角形的性质,平行线的判定等,灵活选择性质和判定定理是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.1全等三角形
学习目标
1.了解全等形和全等三角形的概念.
2.能够找出全等三角形的对应元素.
3.掌握全等三角形的对应边、角相等.
【重点】探究全等三角形的性质.
【难点】掌握两个全等三角形的对应边、对应角的寻找规律,迅速正确地指出两个全等三角形的对应元素.
老师告诉你
全等三角形的性质的作用:
1.求角的度数
2.证明两个角相等
3.求线段的长度
4.证明两条线段相等
5.判断两条直线的位置关系
知识点拨
知识点1 全等图形
形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.
在平面几何中,一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.两个全等形的周长相等,面积相等.
【新知导学】
例1-1.如图所示的各组图形中,不是全等形的是( )
A. B.
C. D.
【对应导练】
1.下列图形中被虚线分成的两部分不是全等形的是( )
A. B.
C. D.
2.下列图标中,不是由全等图形组合成的是( )
A. B.
C. D.
3.下列说法正确的是( )
A. 两个面积相等的图形一定是全等图形
B. 两个正方形是全等图形
C. 若两个图形的周长相等,则它们一定是全等图形
D. 两个全等图形的面积一定相等
4.请观察图中的5组图案,其中是全等形的是_____(填序号).
知识点2 全等三角形及其对应元素
1.全等三角形:能够完全重合的两个三角形叫全等三角形.
2.对应边、对应角、对应顶点的定义:
两个全等三角形重合在一起,重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.
在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角.如下图,△ABC与△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.
3. 找对应边、对应角的方法
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
(3)有公共边的,公共边是对应边;
(4)有公共角的,公共角是对应角;
(5)有对顶角的,对顶角一定是对应角;
(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角),等等.
【新知导学】
例2-1 .下列4个图形中,属于全等的2个图形是_________.(填序号)
例2-2 .已知,且与是对应角,和是对应角,则下列说法中正确的是( )
A.与是对应边 B.与是对应边
C.与是对应边 D.不能确定 的对应边
【对应导练】
1.如图,已知△ABC三条边、三个角,则甲、乙两个三角形中,与△ABC全等的图形是( )
A. 甲 B. 乙 C. 甲和乙 D. 都不是
2 .如图,如果△ABC≌△CDA,∠BAC=∠DCA,∠B=∠D,对于以下结论:
①AB与CD是对应边;②AC与CA是对应边;③点A与点A是对应顶点;④点C与点C是对应顶点;⑤∠ACB与∠CAD是对应角,
其中正确的是( )
A.2个 B.3个 C.4个 D.5个
3 .如下图,与全等.用符号“”表示这两个三角形全等.已知与是对应角,写出其余的对应角和各对对应边.
知识点3 全等三角形的性质
(1)全等三角形的对应边相等;
(2)全等三角形的对应角相等;
后面还会学到:全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.
【新知导学】
例3-1.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数为( )
A. 60° B. 55° C. 65° D. 66°
例3-2.如图,若△ABC≌△DEF,B,E,C,F四点在同一直线上,BC=7,CF=2,则EC的长是( )
A. 2 B. 3 C. 5 D. 7
例3-3.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求∠F的度数与DH的长;
(2)求证:AB∥DE.
【对应导练】
1 .如图,,若,,,则的度数为( )
A. B. C. D.
2.如图,△ABE≌△DCE,点E在线段AD上,点F在CD延长线上,∠F=∠A,求证:AD∥BF.
3.已知,如图∠B=90°,△ABC≌△CDE,B、C、D三点共线.试说明:AC⊥CE.
4.如图,△ABC≌△ADE,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:∠CAE=∠BAD;
(2)若∠BAD=35°,求∠BED的度数.
题型训练
利用全等三角形性质判断两直线的位置
1.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
2.如图,A,D,E三点在同一直线上,且△BAD≌△ACE,试说明:
(1)BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE.
.利用全等三角形求角度
3.如图,△ABC≌△ADE,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:∠CAE=∠BAD;
(2)若∠BAD=35°,求∠BED的度数.
4.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
利用全等三角形求周长
5 .如图,△ACF≌△ADE,AD=12,AE=5,求DF的长.
6.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.
利用全等三角形判断图形形状
7 .如图,D、A、E三点在同一条直线上,BD⊥DE于点D,CE⊥DE于点E,且△ABD≌△CAE,AC=4.
(1)求∠BAC的度数;
(2)判断△ABC的形状,并求△ABC的面积.
牛刀小试
一、单选题(每小题4分,共32分)
1.下列图形中被虚线分成的两部分不是全等形的是( )
A. B.
C. D.
2.下图中全等的三角形是( )
A.①和② B.②和④ C.②和③ D.①和③
3.如图,,且,,则的度数的值为( )
A. B. C. D.
4.如图,,,,则的长度为( )
A. B. C. D.
5.如图,若,则下列结论中一定成立的是( )
A. B. C. D.
6.2.下列图形中是全等形的是( )
A. B.
C. D.
7.如图,点B,E,C,F在同一直线上,,,,则EC的长为( )
A.5 B.4.5 C.4 D.3.5
8.三个全等三角形按如图的形式摆放,则的度数是( )
A. B. C. D.
二、填空题(每小题4分,共20分)
9.已知,且的周长为6,若,则DF的长为_________.
10.如图,D在边上,,,则的度数为______.
11.如图,四边形四边形,若,,,则____________°.
12.如图,在平面直角坐标系中,,则点D的坐标是__________.
13.如图,在正方形中,,延长到点E,使,连接,动点P从点A出发,以每秒的速度沿向终点A运动.设点P的运动时间为t秒,当和全等时,t的值为_____.
三、解答题(共6小题,共48分)
14.(8分)试在下列图形中,沿正方形的网格线(虚线)画线,将图形分割成两个全等的图形.
15.(8分)如图,A,C,E三点在同一直线上,且.
(1)求证:.
(2)若,求证:.
16.(8分)如图,在中,cm,cm,D为AB的中点,点P在线段BC上以3cm/s的速度由点B向点C运动,同时点Q在线段CA上由点C向点A以a cm/s的速度运动,设运动的时间为t s.
(1)求CP的长度(用含t的代数式表示);
(2)若以点C,P,Q为顶点的三角形和以点B,D,P为顶点的三角形全等,且和是对应角,求a的值.
17.(8分)如图,,其中点A,B,C,D在一条直线上.
(1)若,,求的度数;
(2)若cm,cm,求AB的长.
18.(8分)如图,已知,点D在上,与交于点P.
(1)若,,求的 度数.
(2)若,,求与的周长之和.
19.如图,试说明:
(1)
(2)
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.1全等三角形
学习目标
1.了解全等形和全等三角形的概念.
2.能够找出全等三角形的对应元素.
3.掌握全等三角形的对应边、角相等.
【重点】探究全等三角形的性质.
【难点】掌握两个全等三角形的对应边、对应角的寻找规律,迅速正确地指出两个全等三角形的对应元素.
老师告诉你
全等三角形的性质的作用:
1.求角的度数
2.证明两个角相等
3.求线段的长度
4.证明两条线段相等
5.判断两条直线的位置关系
知识点拨
知识点1 全等图形
形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.
在平面几何中,一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.两个全等形的周长相等,面积相等.
【新知导学】
例1-1.如图所示的各组图形中,不是全等形的是( )
A. B.
C. D.
【答案】B
【解析】根据能够完全重合的两个图形是全等图形对各选项分析即可得解.
解:观察发现,A、C、D选项的两个图形都可以完全重合,是全等图形,
B选项中圆与椭圆不可能完全重合,不是全等形.
故选:B.
【对应导练】
1.下列图形中被虚线分成的两部分不是全等形的是( )
A. B.
C. D.
【答案】C
【解析】根据全等形的概念进行判断即可.
解:A、长方形被对角线分成的两部分是全等形;
B、正六边形被对角线分成的两部分是全等形;
C、梯形被对角线分成的两部分不是全等形;
D、圆被对角线分成的两部分是全等形,
故选:C.
2.下列图标中,不是由全等图形组合成的是( )
A. B.
C. D.
【答案】C
【解析】根据全等图形的概念分析即可.
解:A、该图象是由三个全等的图形构成,故该选项不符合题意;
B、该图象是由五个全等的图形构成,故该选项不符合题意;
C、该图象不是由全等图形构成,故该选项符合题意;
D、该图象是由两个全等的图形构成,故该选项不符合题意;
故选:C.
3.下列说法正确的是( )
A. 两个面积相等的图形一定是全等图形
B. 两个正方形是全等图形
C. 若两个图形的周长相等,则它们一定是全等图形
D. 两个全等图形的面积一定相等
【答案】D
【解析】依据全等图形的定义和性质进行判断即可.
解:A、两个面积相等的图形不一定是全等图形,说法错误,不符合题意;
B、两个边长相等的正方形是全等图形,说法错误,不符合题意;
C、若两个图形的周长相等,则它们不一定是全等图形,说法错误,不符合题意;
D、两个全等图形的面积一定相等,说法正确,符合题意;
故选:D.
4.请观察图中的5组图案,其中是全等形的是_____(填序号).
【答案】(1)(4)(5)
【解析】能够完全重合的两个图形叫做全等形,结合所给图形进行判断即可.
解:5组图案,其中是全等形的是(1)(4)(5).
故答案为:是(1)(4)(5).
知识点2 全等三角形及其对应元素
1.全等三角形:能够完全重合的两个三角形叫全等三角形.
2.对应边、对应角、对应顶点的定义:
两个全等三角形重合在一起,重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.
在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角.如下图,△ABC与△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.
3. 找对应边、对应角的方法
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
(3)有公共边的,公共边是对应边;
(4)有公共角的,公共角是对应角;
(5)有对顶角的,对顶角一定是对应角;
(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角),等等.
【新知导学】
例2-1 .下列4个图形中,属于全等的2个图形是_________.(填序号)
【答案】①③
【分析】先求出的度数,然后分析求解即可.
【详解】解:在③中,,
∴与①中的相等,并且两夹边对应相等,
∴属于全等的2个图形是①③
故答案为①③.
【点评】本题考查了三角形全等的条件,熟悉全等三角形的判定定理是解题的关键.
例2-2 .已知,且与是对应角,和是对应角,则下列说法中正确的是( )
A.与是对应边 B.与是对应边
C.与是对应边 D.不能确定 的对应边
【答案】A
【分析】根据全等三角形的概念即可得到答案.
解:与是对应角,和是对应角,
和是对应角,
与是对应边,
故选A.
【点拨】本题考查了全等三角形,理解全等三角形的概念,准确找出对应边是解题关键.
【对应导练】
1.如图,已知△ABC三条边、三个角,则甲、乙两个三角形中,与△ABC全等的图形是( )
A. 甲 B. 乙 C. 甲和乙 D. 都不是
【答案】C
【解析】甲可根据ASA判定与△ABC全等;乙可根据AAS判定与△ABC全等,可得答案.
解:甲三角形夹b边的两角分别与已知三角形对应相等,故甲与△ABC全等;
乙三角形50°内角及所对边与△ABC对应相等且均有70°内角,可根据AAS判定乙与△ABC全等;
则与△ABC全等的有乙和甲,
故选:C.
2 .如图,如果△ABC≌△CDA,∠BAC=∠DCA,∠B=∠D,对于以下结论:
①AB与CD是对应边;②AC与CA是对应边;③点A与点A是对应顶点;④点C与点C是对应顶点;⑤∠ACB与∠CAD是对应角,
其中正确的是( )
A.2个 B.3个 C.4个 D.5个
【答案】B
【分析】由全等三角形的对应边相等、对应角相等对以下结论进行判定.
【详解】解:△ABC≌△CDA,∠BAC=∠DCA,∠B=∠D.
①AB与CD是对应边.故①正确;
②AC与CA是对应边.故②正确;
③点A与点C是对应顶点.故③错误;
④点C与点A是对应顶点.故④错误;
⑤∠ACB与∠CAD是对应角.故⑤正确.
综上所述,正确的结论是①②⑤,共有3个.
故选B.
3 .如下图,与全等.用符号“”表示这两个三角形全等.已知与是对应角,写出其余的对应角和各对对应边.
【答案】.对应角是:与,与;
对应边是;OA与OB,OC与OD,AC与BD.
【分析】根据全等三角形的表示法以及全等三角形的性质即可得到答案.
解: .
因为与是对应角,所以其余的对应角是:
与,与;
对应边是;OA与OB,OC与OD,AC与BD.
【点拨】本题主要考查全等三角形的表示法和性质,准确找到全等三角形的对应角和对应边是关键.
知识点3 全等三角形的性质
(1)全等三角形的对应边相等;
(2)全等三角形的对应角相等;
后面还会学到:全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.
【新知导学】
例3-1.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数为( )
A. 60° B. 55° C. 65° D. 66°
【答案】C
【解析】直接利用全等三角形的性质得出∠1=∠2进而得出答案.
解:∵如图是两个全等三角形,
∴∠1=∠2=180°-60°-55°=65°.
故选:C.
例3-2.如图,若△ABC≌△DEF,B,E,C,F四点在同一直线上,BC=7,CF=2,则EC的长是( )
A. 2 B. 3 C. 5 D. 7
【答案】C
【解析】利用全等三角形的性质可得BC=EF=7,再利用线段的和差关系计算即可.
解:∵△ABC≌△DEF,
∴BC=EF=7,
∴CF=2,
∴EC=EF-CF=7-2=5,
故选:C.
例3-3.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求∠F的度数与DH的长;
(2)求证:AB∥DE.
【解析】(1)根据三角形内角和定理求出∠ACB,根据全等三角形的性质得出AB=DE,∠F=∠ACB,即可得出答案;
(2)根据全等三角形的性质得出∠B=∠DEF,根据平行线的判定得出即可.
解:(1)∵∠A=85°,∠B=60°,
∴∠ACB=180°-∠A-∠B=35°,
∵△ABC≌△DEF,AB=8,
∴∠F=∠ACB=35°,DE=AB=8,
∵EH=2,
∴DH=8-2=6;
(2)证明:∵△ABC≌△DEF,
∴∠DEF=∠B,
∴AB∥DE.
【对应导练】
1 .如图,,若,,,则的度数为( )
A. B. C. D.
【答案】C
【分析】首先根据三角形内角和定理求出,然后根据全等三角形的性质得到,,最后利用三角形外角的性质求解即可.
解:∵,,
∴
∵
∴
∵
∴,
∴
∴.
故选:C.
【点拨】本题考查了全等三角形的性质和三角形内角和定理的应用,三角形外角的性质,解题的关键是掌握以上知识点,全等三角形的对应角相等,对应边相等.
2.如图,△ABE≌△DCE,点E在线段AD上,点F在CD延长线上,∠F=∠A,求证:AD∥BF.
【解析】根据△ABE≌△DCE得到∠A=∠ADC,然后利用∠F=∠A得到∠F=∠EDC,利用同位角相等,两直线平行证得结论.
证明:∵△ABE≌△DCE,
∴∠A=∠ADC,
∵∠F=∠A,
∴∠F=∠EDC,
∴AD∥BF.
3.已知,如图∠B=90°,△ABC≌△CDE,B、C、D三点共线.试说明:AC⊥CE.
【解析】根据Rt△ABC≌Rt△CDE可得∠BCA=∠CED,再根据直角三角形两锐角互余可得∠CED+∠ECD=90°,进而得到∠BCA+∠ECD=90°,再根据角之间的关系可得∠ACE=90°.
证明:∵∠B=90°,△ABC≌△CDE,
∴∠D=90°,
∴∠BCA=∠CED,
∵△DCE是直角三角形,
∴∠CED+∠ECD=90°,
∴∠BCA+∠ECD=90°,
∴∠ACE=180°-90°=90°,
∴AC⊥CE.
4.如图,△ABC≌△ADE,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:∠CAE=∠BAD;
(2)若∠BAD=35°,求∠BED的度数.
【解析】(1)根据全等三角形的性质得出∠BAC=∠DAE,再求出答案即可;
(2)根据全等三角形的性质得出∠D=∠B,根据对顶角相等和三角形内角和定理得出∠AFD=∠EFB,∠D+∠BAD+∠AFD=180°,∠B+∠EFB+∠BED=180°,求出∠BED=∠BAD即可.
(1)证明:∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC-∠BAE=∠DAE-∠BAE,
∴∠CAE=∠BAD;
(2)解:∵△ABC≌△ADE,
∴∠D=∠B,
∵∠AFD=∠EFB,∠D+∠BAD+∠AFD=180°,∠B+∠EFB+∠BED=180°,
∴∠BED=∠BAD,
∵∠BAD=35°,
∴∠BED=35°.
题型训练
利用全等三角形性质判断两直线的位置
1.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
【解析】(1)根据平行线性质求出∠A=∠B,根据SAS推出即可.
(2)根据全等三角形性质推出CD=CE,根据等腰三角形性质求出即可.
证明:(1)∵AD∥BE,
∴∠A=∠B,
在△ACD和△BEC中
∴△ACD≌△BEC(SAS),
(2)∵△ACD≌△BEC,
∴CD=CE,
又∵CF平分∠DCE,
∴CF⊥DE.
2.如图,A,D,E三点在同一直线上,且△BAD≌△ACE,试说明:
(1)BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE.
【答案】(1)证明见解析;(2)∠ADB=90°.
【分析】(1)根据全等三角形的性质求出BD=AE,AD=CE,代入求出即可;
(2)根据全等三角形的性质求出∠E=∠BDA=90°,推出∠BDE=90°,根据平行线的判定求出即可.
【详解】解:(1)∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE;
(2)△ABD满足∠ADB=90°时,BD∥CE,
理由是:∵△BAD≌△ACE,
∴∠E=∠ADB=90°,
∴∠BDE=180° 90°=90°=∠E,
∴BD∥CE.
【点评】本题考查了全等三角形的性质和平行线的判定等的应用,关键是通过三角形全等得出正确的结论,通过做此题培养了学生分析问题的能力.
.利用全等三角形求角度
3.如图,△ABC≌△ADE,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:∠CAE=∠BAD;
(2)若∠BAD=35°,求∠BED的度数.
【解析】(1)根据全等三角形的性质得出∠BAC=∠DAE,再求出答案即可;
(2)根据全等三角形的性质得出∠D=∠B,根据对顶角相等和三角形内角和定理得出∠AFD=∠EFB,∠D+∠BAD+∠AFD=180°,∠B+∠EFB+∠BED=180°,求出∠BED=∠BAD即可.
(1)证明:∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC-∠BAE=∠DAE-∠BAE,
∴∠CAE=∠BAD;
(2)解:∵△ABC≌△ADE,
∴∠D=∠B,
∵∠AFD=∠EFB,∠D+∠BAD+∠AFD=180°,∠B+∠EFB+∠BED=180°,
∴∠BED=∠BAD,
∵∠BAD=35°,
∴∠BED=35°.
4.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
【解析】(1)根据全等三角形的性质得到AB=DE=10,BE=BC=4,结合图形计算,得到答案;
(2)根据全等三角形的性质得到∠BAC=∠D=30°,∠DBE=∠C=70°,根据三角形内角和定理求出∠ABC,计算即可.
解:(1)∵△ABC≌△DEB,DE=10,BC=4,
∴AB=DE=10,BE=BC=4,
∴AE=AB-BE=6;
(2)∵△ABC≌△DEB,∠D=30°,∠C=70°,
∴∠BAC=∠D=30°,∠DBE=∠C=70°,
∴∠ABC=180°-30°-70°=80°,
∴∠DBC=∠ABC-∠DBE=10°.
利用全等三角形求周长
5 .如图,△ACF≌△ADE,AD=12,AE=5,求DF的长.
【解析】直接利用全等三角形的性质得出AC=AD,进而得出答案.
解:∵△ACF≌△ADE,AD=12,AE=5,
∴AC=AD=12,AE=AF=5,
∴DF=12-5=7.
6.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.
【解析】(1)根据全等三角形的性质得到∠ABC=∠DBE,计算即可;
(2)根据全等三角形的性质求出BE、DE,根据三角形的周长公式计算即可.
解:(1)∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,
∴∠ABD=∠CBE=132°÷2=66°,
即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,
∴DE=AC=AD+DC=5,BE=BC=4,
∴△CDP与△BEP的周长和=DC+DP+PC+BP+PE+BE=DC+DE+BC+BE=2.5+5+4+4=15.5.
利用全等三角形判断图形形状
7 .如图,D、A、E三点在同一条直线上,BD⊥DE于点D,CE⊥DE于点E,且△ABD≌△CAE,AC=4.
(1)求∠BAC的度数;
(2)判断△ABC的形状,并求△ABC的面积.
【答案】(1)90°
等腰直角三角形,8
【分析】(1)根据垂直的定义得到∠D=90°,求得∠DBA+∠BAD=90°,根据全等三角形的性质得到∠DBA=∠CAE,等量代换即可得到结论;
(2)根据全等三角形的性质得AC=AB=4,再根据三角形的面积求出答案.
【详解】(1)解:∵BD⊥DE,
∴∠D=90°,
∴∠DBA+∠BAD=90°,
∵△ABD≌△CAE,
∴∠DBA=∠CAE
∴∠BAD+∠CAE=90°,
∴∠BAC=90°;
(2)解:∵△ABD≌△CAE,
∴AC=AB=4,
又∵∠BAC=90°
∴△ABC是等腰直角三角形,
∴△ABC的面积=4×4÷2=8.
【点评】本题考查的是全等三角形的性质、三角形的面积公式,证得△ABC是直角三角形是解决本题的关键.
牛刀小试
一、单选题(每小题4分,共32分)
1.下列图形中被虚线分成的两部分不是全等形的是( )
A. B.
C. D.
【答案】:A
解析:观察选项可知,选项B,C,D中的虚线把图形分成全等的两部分,
故选:A.
【点评】此题主要考查了全等图形,关键是掌握能够完全重合的两个图形叫做全等形.
2.下图中全等的三角形是( )
A.①和② B.②和④ C.②和③ D.①和③
【答案】D
解析:A、①和②,SA,角的另一条邻边不相等,两个三角形不全等,不符合题意;
B、②和④,5cm分别是图②和图④30°的邻边和对边,两个三角形不全等,不符合题意;
C、②和③,SA,角的另一条邻边不相等,两个三角形不全等,不符合题意;
D、①和③,SAS,两个三角形全等,符合题意;
故选D.
【点拨】本题考查了全等三角形,理解全等三角形的概念,准确找出对应边是解题关键.
3.如图,,且,,则的度数的值为( )
A. B. C. D.
【答案】D
解析:,,
,,
,
,
,
.
故选:D.
【点拨】本题考查了全等三角形的性质和三角形内角和定理的应用,三角形外角的性质,解题的关键是掌握以上知识点,全等三角形的对应角相等,对应边相等.
4.如图,,,,则的长度为( )
A. B. C. D.
【答案】B
解析:,
,,
.
故选:B.
【点评】此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应边相等.
5.如图,若,则下列结论中一定成立的是( )
A. B. C. D.
【答案】:B
解析:,
,,,,
,
即.
故A,C,D选项错误,B选项正确,
故选:B.
【点拨】本题考查了全等三角形的性质,,结合图形和题意找到角之间的关系是解题的关键.
6.2.下列图形中是全等形的是( )
A. B.
C. D.
【答案】:D
解析:A.两个图形不能完全重合,不是全等形;
B.两个图形不能完全重合,不是全等形;
C.两个图形不能完全重合,不是全等形;
D.两个图形能完全重合,是全等形;
故选:D.
【点评】此题主要考查了全等图形,关键是掌握能够完全重合的两个图形叫做全等形.
7.如图,点B,E,C,F在同一直线上,,,,则EC的长为( )
A.5 B.4.5 C.4 D.3.5
【答案】:B
解析:,,
,
,,
,
,
故选:B.
【点评】此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应边相等.
8.三个全等三角形按如图的形式摆放,则的度数是( )
A. B. C. D.
【答案】D
解析:如图所示:
由图形可得:,
三个全等三角形,
,
又,
,
的度数是.
故选:D.
【点拨】本题考查了全等三角形的性质,三角形内角和,结合图形和题意找到角之间的关系是解题的关键.
二、填空题(每小题4分,共20分)
9.已知,且的周长为6,若,则DF的长为_________.
【答案】2.1
解析:,,
,
的周长为6,
,
故答案为:2.1.
【点评】此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应边相等。
10.如图,D在边上,,,则的度数为______.
【答案】
解析:,
,,
,,
中,,
,
故答案为:.
【点评】此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应角相等.
11.如图,四边形四边形,若,,,则____________°.
【答案】105
解析:四边形四边形,
,,
,
,
,,
,
,
故答案为:105.
【点评】本题主要考查了全等图形的定义,解题的关键是熟练掌握形状和大小都相同的图形是全等图形.
12.如图,在平面直角坐标系中,,则点D的坐标是__________.
【答案】
解析:,,点D的坐标是.
【点评】本题主要考查了坐标与图形,全等三角形的性质,掌握全等三角形性质是解题的关键.
13.如图,在正方形中,,延长到点E,使,连接,动点P从点A出发,以每秒的速度沿向终点A运动.设点P的运动时间为t秒,当和全等时,t的值为_____.
答案:2或7
解析:正方形ABCD,
,,
是直角三角形,
为直角三角形,
点P只能在上或者上,
当点P在上时,如图,当时,有,
,
,
,
当点P在上时,则当时,有,
,
故答案为:2或7.
【点评】本题考查了全等三角形的性质,明确全等三角形的对应角所对的边为对应边是解本题的关键.
三、解答题(共6小题,共48分)
14.(8分)试在下列图形中,沿正方形的网格线(虚线)画线,将图形分割成两个全等的图形.
答案:如图所示.
解析:
15.(8分)如图,A,C,E三点在同一直线上,且.
(1)求证:.
(2)若,求证:.
答案:(1)见解析
(2)见解析
解析:(1),
,,
,
;
(2),
,,
,
.
【点评】本题考查了全等三角形的性质和平行线的判定等的应用,关键是通过三角形全等得出正确的结论,通过做此题培养了学生分析问题的能力.
16.(8分)如图,在中,cm,cm,D为AB的中点,点P在线段BC上以3cm/s的速度由点B向点C运动,同时点Q在线段CA上由点C向点A以a cm/s的速度运动,设运动的时间为t s.
(1)求CP的长度(用含t的代数式表示);
(2)若以点C,P,Q为顶点的三角形和以点B,D,P为顶点的三角形全等,且和是对应角,求a的值.
答案:(1)因为cm,cm,
所以cm.
(2)①当时,因为,D为AB的中点,
所以,所以,解得.
此时,
所以,即,解得.
②当时,,解得.
此时,
所以,即,解得.
综上所述,a的值为3或.
【点评】本题主要考查了全等三角形的性质,利用分类讨论思想解答是解题的关键.
17.(8分)如图,,其中点A,B,C,D在一条直线上.
(1)若,,求的度数;
(2)若cm,cm,求AB的长.
答案:(1),.
,
,
.
(2),,
,即.
cm,cm,
(cm),
cm.
【点评】此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应边相等;全等三角形的对应角相等.
18.(8分)如图,已知,点D在上,与交于点P.
(1)若,,求的 度数.
(2)若,,求与的周长之和.
答案:(1),
,
即,
(2),
,
【点拨】本题考查全等三角形的性质,掌握全等三角形的性质是解题的关键.
19.如图,试说明:
(1)
(2)
答案:(1)
(2)时,
理由如下: (添加的条件是)
【点评】本题主要考查了全等三角形的性质,平行线的判定等,灵活选择性质和判定定理是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
