沪教版2024-2025学年六年级上册同步提升讲义第11讲一次式(六大题型)(学生版+解析)
文档属性
| 名称 | 沪教版2024-2025学年六年级上册同步提升讲义第11讲一次式(六大题型)(学生版+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 494.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-08 16:37:26 | ||
图片预览




文档简介
第11讲 一次式(六大题型)
学习目标
1、知道一次式的有关概念 2. 学会合并一次式的同类项; 3、了解一次式的加减及求值、应用等; 4、掌握数与一次式相乘。
一、一次式
代数式5x-3y+4是5.x、-3y和4的和,我们把5x、-3y、4称作代数式5-3y+4的项.
数相乘时,把这个数与项的系数相乘的积作为字母的系数,字母不变.运算时要注意这个数与项的系数相乘的积的符号.
【方法规律】 式子2×(5a-2)中问的乘号可以省略不写、简记为2(5a-2).
【即学即练1】指出一次式5m--8中的一次项、常数项及一次项的系数
【即学即练2】指出并合并一次式7m+4n-3-m-6n+5中的同类项.
【即学即练3】先去括号,再合并同类项:
(1)a+2-(9a-3);
(2)—(6m-8)一(-1+2m)。
题型1:一次式的有关概念
【典例1】.指出下列一次式的一次项、常数项和一次项的系数:
m、a+b、-2、、3a-b-9
题型2:合并同类项、一次式加减
【典例2】..先去括号,再合并同类项.
(1)(2-6x)+(3x+3);
(2)—(5y-10)-(2-2y).
【典例3】 (1)求一次式2x、3-4x、x+1的和;
(2)求3m-2n+1减去m+n-2的差。
题型3:一次式加减并求值
【典例4】.当x=时,求一次式3x-1+(3x-6)-(-3x+1)的值.
题型4:一次式加减的实际应用
【典例5】.某汽车企业第一季度销售x万辆新能源汽车,第二季度销售的新能源汽车比第一季度的1.5倍少1万辆,第三季度销售的新能源汽车比第一季度的2倍多6万辆.用一次式表示;
(1)该汽车企业第二季度和第三季度一共销售的新能源汽车数量;
(2)第三季度比第二季度多销售的新能源汽车数量.
分析 第二季度销售的新能源汽车数量:(1.5x-1)万辆;
第三季度销售的新能源汽车数量(2x+6)万辆。
因此,第二季度和第三垂度一共销售[(1.5x-1)+(2x+6)]万辆;
第三季度比第二季度多销售[(2.x+6)—(1.5x-1)]万辆。
题型5:数与一次式相乘
【典例6】. 计算:
(1)6(m-3);
(2)-7(n—3m);
(3)-x+2(3x-2);
(4)3(2x+1)-2(1-x).
题型6:一次式有关的图形问题
【典例20】.如图2-3-2,用一根铁丝围成一个长方形,这个长方形的宽是a cm,它的长是(3a-2)cm.如何用一次式表示这根铁丝的长度
一、单选题、填空、解答题
1.找出下列代数式中的一次式:
a+3、5-2y 、3x、-9、-、x+y-1.
2.合并同类项:
(1)3m+6m=_______
(2)2m-6m=______;
(3)-2m-6m=_______;
(4)5m+6m=______.
3.判断下列各式是否正确,正确的在括号里打“√”,错误的在括号 里打“×”:
篇文稿的总字数
用16块面积都是S的正方形地砖铺一块正方形的地面,中间4块地砖是蓝色地砖,其他的12 块地砖都是白色地砖,如图2-3-1所示。如何用一次式表示白色地砖总面积
图2-3-1
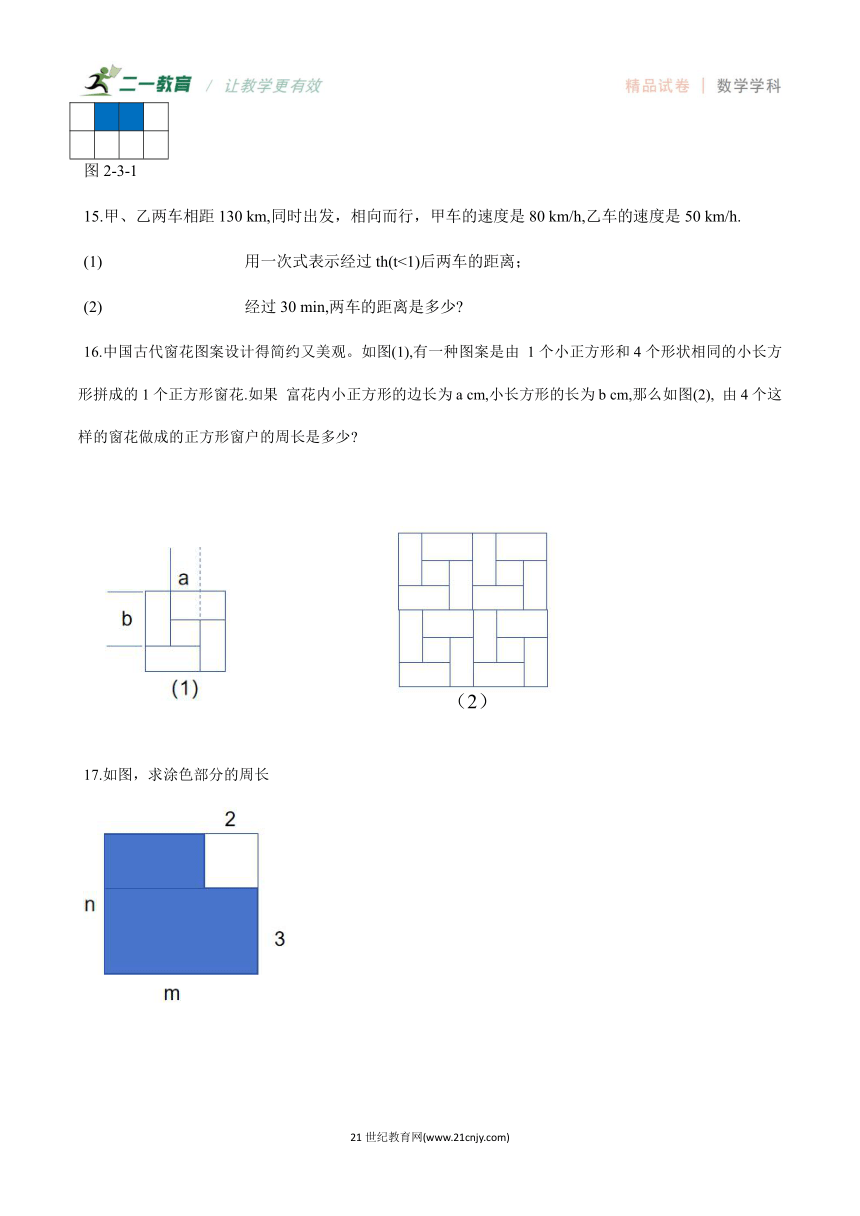
15.甲、乙两车相距130 km,同时出发,相向而行,甲车的速度是80 km/h,乙车的速度是50 km/h.
用一次式表示经过th(t<1)后两车的距离;
经过30 min,两车的距离是多少
16.中国古代窗花图案设计得简约又美观。如图(1),有一种图案是由 1个小正方形和4个形状相同的小长方形拼成的1个正方形窗花.如果 富花内小正方形的边长为a cm,小长方形的长为b cm,那么如图(2), 由4个这样的窗花做成的正方形窗户的周长是多少
17.如图,求涂色部分的周长
强化训练补
1.下列代数式是一次式的是( )
A.8 B.4s+3t C.xy D.
2.已知(a﹣1)x3+xb﹣1是关于x的一次式,则a,b的值分别是( )
A.0,3 B.0,1 C.1,2 D.1,1
3.式子(a﹣1)x3+x(b﹣1)是关于x的一次式,则a、b的值可能为( )
A.0,1 B.1,2 C.0,3 D.1,1
4.一次式M与﹣2x+3y的和是﹣5x+2y,则M等于( )
A.﹣7x+5y B.3x+y C.﹣3x﹣y D.7x﹣5y
5.一次式1﹣y+2x的第二项是 ,第三项的系数是 .
6.一次式中b的系数是 ,常数项是 .
7.若一次式3a+2b﹣1的值为3,那么一次式6a﹣5+4b= .
8.已知(n﹣3)xn﹣1+x﹣2是关于x的一次式,约定x0=1(x≠0),求n的值.
第11讲 一次式(六大题型)
学习目标
1、知道一次式的有关概念 2. 学会合并一次式的同类项; 3、了解一次式的加减及求值、应用等; 4、掌握数与一次式相乘。
一、一次式
代数式5x-3y+4是5.x、-3y和4的和,我们把5x、-3y、4称作代数式5-3y+4的项.
x、-3y只含有一个字母,且字母的指数是1,叫作一次项.不含字母的项叫作常数项,一次项中的数字因数叫作项的数字系数,简称系数.例如,5.x的系数是5,-3y的系数是-3;代数式-x+2y的一次项是一x和2y,一次项的系数分别是一1和2.
【方法规律】x和-x的系数分别是1、一1,而系数 “1”遇常省略不写.
像这样,由一次项与常数项组成,或仅含一次项的代数式叫作一次式.
例-2b、7-、6m+7m、 等都是一次式,但m 、 a-b 、6+3c-c2、-9等都不是一次式.
二、一次式的同类项
一次式5x+3x中的5.x、3x这两项所含字母相同,一次式16S-4S中的16S、-4S这两项所含字母也相同.在一次式中,字母相同的项叫作一次式的同类项,所有常数项都是同类项.
一次式中含字母的同类项可以合并,合并时只要把含字母的同类项的系数相加
一般地,把同类项合并成一项,称为合并同类项.合并一次式的同类项时,把含字母的同类项的系数相加所得的结果作为系数,字母不变;常数项直接相加.
三、一次式的加减
思考:如何计算(2.5x-2)+(3x+8)和(2.5x+8)-(1.5x-3)
数的运算中的去括号方法在一次式中同样适用,即括号前面是“+”号, 去掉括号后,括号内各项都不变;括号前面是“一”号,去掉括号后,括号内各项都变号.
如下所示,根据去括号方法区我们可以分别求出(2.5x-2)+(3x+8)和(2.5x+8)-(1.5x-3)的结果
【方法规律】几个一次式相加减,通常用括号把每个一次式括起来,再用加减号连接。
四、数与一次式相乘
一般地,数与一次式相乘,就是用这个数去乘一次式的每一项,再把所得的积相加.在含有字母的项与数相乘时,把这个数与项的系数相乘的积作为字母的系数,字母不变.运算时要注意这个数与项的系数相乘的积的符号.
【方法规律】 式子2×(5a-2)中问的乘号可以省略不写、简记为2(5a-2).
【即学即练1】 指出一次式5m--8中的一次项、常数项及一次项的系数
【答案】解:一次式5m--8中的一次项是5m和-,常数项是-8,其中
一次项的系数分别是5、-
【即学即练2】指出并合并一次式7m+4n-3-m-6n+5中的同类项.
【答案】解:一次式7m+4n-3-m-6m+5中,7m和-m是同类项,4n和-6n是同类项,-3和5是同类项
因为7m+4n-3-m-6n+5就是7m、4n、-3、-m、-6n、5的和,
所以根据加法的交换律和结合律,得
7m+4n-3-m-6n+5
=7m-m+4n-6n-3+5(加法交换律)
=(7m—m)+(4n-6n)+(-3+5)(加法结合律)
=(7-1)m+(4-6)n+2(合并同类项)
=6m-2n+2.
【即学即练3】先去括号,再合并同类项:
(1)a+2-(9a-3);
(2)—(6m-8)一(-1+2m)。
【答案】 解:(1)a+2—(9a-3)
=a+2-9a+3
=-8a+5.
(2)—(6m-8)-(-1+2m)
= —6m+8+1-2m
=—8m+9.
题型1:一次式的有关概念
【典例1】.指出下列一次式的一次项、常数项和一次项的系数:
(1)6(m-3);
(2)-7(n—3m);
(3)-x+2(3x-2);
(4)3(2x+1)-2(1-x).
【答案】解(1)6(m-3)
=6m+6×(-3)
=6m—18.
(2)—7(n—3m)
=—7n+(-7)×(-3m)
=—7n+21m
(3)-x+2(3x-2)
= -x+6x—4
=5x-4.
(4)3(2x+1)-2(1-x)
=6x+3-2+2x
=8x+1
题型6:一次式有关的图形问题
【典例20】.如图2-3-2,用一根铁丝围成一个长方形,这个长方形的宽是a cm,它的长是(3a-2)cm.如何用一次式表示这根铁丝的长度
【答案】根据题意,铁丝的长为2×(a+3a-2),即2(4a-2)cm
式子2×(4a-2)中问的乘号可以省略不写、简记为2(4a-2).
根据乘法对加法的分配律与乘法结合律,得
2(4a-2)=2×(4a)+2×(-2)(乘法对加法的分配律)
=(2×4)a—4(乘法结合律)
=8a-4.
一、单选题、填空、解答题
1.找出下列代数式中的一次式:
a+3、5-2y 、3x、-9、-、x+y-1.
【答案】略
2.合并同类项:
(1)3m+6m=_______
(2)2m-6m=______;
(3)-2m-6m=_______;
(4)5m+6m=______.
【答案】9m;-4m;-8m;11m
3.判断下列各式是否正确,正确的在括号里打“√”,错误的在括号 里打“×”:
(1)8-6x=2x; ( )
(2)-2y+2y=-4 ( )
(3)3m+4n=7mn; ( )
(4)4m+6m=16m. ( )
【答案】×;×;×;×
4.化简下列一次式:
(1)7m-2-7n+3m;
(2)-5+2m-1
【答案】10m-7n-2;
5.(1)求4x-5与2-y+6x的和;
(2)求5m减去4n-3m+1的差.
【答案】10x-y-3;8m-4n-1
6.先化商,再求值:(2x-y)-(x+y-3),其中x=1,y=-1.
【答案】6
7.计算:
(1)-2(m+6);
(2)-3(n—8);
(3)(-3x+5)×(-5);
(4)(5y-3)×(-3).
【答案】-2m-12;-3n+24;15x-25;-3y+9
8.计算
(1)2(x-3)—5x;
图2-3-1
【答案】解:由图可以知道,正方形地面总面积是16S,蓝色地砖总面积是4S,白色地砖总面积是12S.白色地砖总面积也等于正方形地面总面积减去蓝色地砖总面积,
图2-3-1
由此可以得到
16S-4S=12S,
即16S-4S=(16-4)S
15.甲、乙两车相距130 km,同时出发,相向而行,甲车的速度是80 km/h,乙车的速度是50 km/h.
用一次式表示经过th(t<1)后两车的距离;
经过30 min,两车的距离是多少
【答案】解:
(1)根据题意,经过t/h(t<1)后两车的距离为
(80t+50t)
=130-130t(km).
答:经过th(t<1),两车的距离为(130-130t)km
(2)因为30min=h,时,
有130-130t=130-130×=65(km).
答:经过30 min,两车的距离是65 km
16.中国古代窗花图案设计得简约又美观。如图(1),有一种图案是由 1个小正方形和4个形状相同的小长方形拼成的1个正方形窗花.如果 富花内小正方形的边长为a cm,小长方形的长为b cm,那么如图(2), 由4个这样的窗花做成的正方形窗户的周长是多少
【答案】 8a+8b
17.如图,求涂色部分的周长
【答案】 略
强化训练
1.下列代数式是一次式的是( )
A.8 B.4s+3t C.xy D.
【分析】根据单项式的次数是字母指数的和,多项式的次数是多项式中次数最高的单项式的次数,可得答案.
【解析】解:A、8的次数是0,故A错误;
B、次数是1,故B正确;
C、次数是2,故C错误;
D、是分式,次数是﹣1,故D错误;
故选:B.
2.已知(a﹣1)x3+xb﹣1是关于x的一次式,则a,b的值分别是( )
A.0,3 B.0,1 C.1,2 D.1,1
【分析】根据代数式的定义进行解题即可.
【解析】解:由题可知,a﹣1=0,b﹣1=1,
则a=1,b=2,
故选:C.
3.式子(a﹣1)x3+x(b﹣1)是关于x的一次式,则a、b的值可能为( )
A.0,1 B.1,2 C.0,3 D.1,1
【分析】根据题意得出a﹣1=0,b﹣1≠0,求出a和b的值,再结合给出的选项即可得出答案.
【解析】解:∵多项式(a﹣1)x3+x(b﹣1)是关于x的一次式,
∴a﹣1=0,b﹣1≠0,
∴a=1,b≠1,
∴a、b的值可能为1,2;
故选:B.
4.一次式M与﹣2x+3y的和是﹣5x+2y,则M等于( )
A.﹣7x+5y B.3x+y C.﹣3x﹣y D.7x﹣5y
【分析】本题考查整式的加减运算,解答时合并同类项即可.
根据已知条件可设此多项式为M建立等式解得即可.
【解析】解:M=(﹣5x+2y)﹣(﹣2x+3y)
=﹣5x+2y+2x﹣3y
=﹣3x﹣y
故选:C.
5.一次式1﹣y+2x的第二项是 ﹣y ,第三项的系数是 2 .
【分析】根据多项式的项及单项式的系数的定义求解.
【解析】解:一次式1﹣y+2x是1,﹣y,2x这三个单项式的和,所以第二项是﹣y,第三项2x的系数是2.
故答案为﹣y,2.
6.一次式中b的系数是 ﹣ ,常数项是 1 .
【分析】根据单项式的系数和常数项的定义解答.
【解析】解:一次式中b的系数是﹣,常数项是1.
7.若一次式3a+2b﹣1的值为3,那么一次式6a﹣5+4b= 3 .
【分析】根据题意列出关系式,所求式子变形后将关系式的值代入计算即可求出值.
【解析】解:∵3a+2b﹣1=3,即3a+2b=4,
∴6a﹣5+4b=2(3a+2b)﹣5=8﹣5=3.
故答案为:3
8.已知(n﹣3)xn﹣1+x﹣2是关于x的一次式,约定x0=1(x≠0),求n的值.
【分析】根据一次式的定义得到n﹣1=0或n﹣1=1或n﹣3=0,易求n的值.
【解析】解:∵(n﹣3)xn﹣1+x﹣2是关于x的一次式,约定x0=1(x≠0),
∴n﹣1=0或n﹣1=1或n﹣3=0,
21世纪教育网(www.21cnjy.com)
学习目标
1、知道一次式的有关概念 2. 学会合并一次式的同类项; 3、了解一次式的加减及求值、应用等; 4、掌握数与一次式相乘。
一、一次式
代数式5x-3y+4是5.x、-3y和4的和,我们把5x、-3y、4称作代数式5-3y+4的项.
数相乘时,把这个数与项的系数相乘的积作为字母的系数,字母不变.运算时要注意这个数与项的系数相乘的积的符号.
【方法规律】 式子2×(5a-2)中问的乘号可以省略不写、简记为2(5a-2).
【即学即练1】指出一次式5m--8中的一次项、常数项及一次项的系数
【即学即练2】指出并合并一次式7m+4n-3-m-6n+5中的同类项.
【即学即练3】先去括号,再合并同类项:
(1)a+2-(9a-3);
(2)—(6m-8)一(-1+2m)。
题型1:一次式的有关概念
【典例1】.指出下列一次式的一次项、常数项和一次项的系数:
m、a+b、-2、、3a-b-9
题型2:合并同类项、一次式加减
【典例2】..先去括号,再合并同类项.
(1)(2-6x)+(3x+3);
(2)—(5y-10)-(2-2y).
【典例3】 (1)求一次式2x、3-4x、x+1的和;
(2)求3m-2n+1减去m+n-2的差。
题型3:一次式加减并求值
【典例4】.当x=时,求一次式3x-1+(3x-6)-(-3x+1)的值.
题型4:一次式加减的实际应用
【典例5】.某汽车企业第一季度销售x万辆新能源汽车,第二季度销售的新能源汽车比第一季度的1.5倍少1万辆,第三季度销售的新能源汽车比第一季度的2倍多6万辆.用一次式表示;
(1)该汽车企业第二季度和第三季度一共销售的新能源汽车数量;
(2)第三季度比第二季度多销售的新能源汽车数量.
分析 第二季度销售的新能源汽车数量:(1.5x-1)万辆;
第三季度销售的新能源汽车数量(2x+6)万辆。
因此,第二季度和第三垂度一共销售[(1.5x-1)+(2x+6)]万辆;
第三季度比第二季度多销售[(2.x+6)—(1.5x-1)]万辆。
题型5:数与一次式相乘
【典例6】. 计算:
(1)6(m-3);
(2)-7(n—3m);
(3)-x+2(3x-2);
(4)3(2x+1)-2(1-x).
题型6:一次式有关的图形问题
【典例20】.如图2-3-2,用一根铁丝围成一个长方形,这个长方形的宽是a cm,它的长是(3a-2)cm.如何用一次式表示这根铁丝的长度
一、单选题、填空、解答题
1.找出下列代数式中的一次式:
a+3、5-2y 、3x、-9、-、x+y-1.
2.合并同类项:
(1)3m+6m=_______
(2)2m-6m=______;
(3)-2m-6m=_______;
(4)5m+6m=______.
3.判断下列各式是否正确,正确的在括号里打“√”,错误的在括号 里打“×”:
篇文稿的总字数
用16块面积都是S的正方形地砖铺一块正方形的地面,中间4块地砖是蓝色地砖,其他的12 块地砖都是白色地砖,如图2-3-1所示。如何用一次式表示白色地砖总面积
图2-3-1
15.甲、乙两车相距130 km,同时出发,相向而行,甲车的速度是80 km/h,乙车的速度是50 km/h.
用一次式表示经过th(t<1)后两车的距离;
经过30 min,两车的距离是多少
16.中国古代窗花图案设计得简约又美观。如图(1),有一种图案是由 1个小正方形和4个形状相同的小长方形拼成的1个正方形窗花.如果 富花内小正方形的边长为a cm,小长方形的长为b cm,那么如图(2), 由4个这样的窗花做成的正方形窗户的周长是多少
17.如图,求涂色部分的周长
强化训练补
1.下列代数式是一次式的是( )
A.8 B.4s+3t C.xy D.
2.已知(a﹣1)x3+xb﹣1是关于x的一次式,则a,b的值分别是( )
A.0,3 B.0,1 C.1,2 D.1,1
3.式子(a﹣1)x3+x(b﹣1)是关于x的一次式,则a、b的值可能为( )
A.0,1 B.1,2 C.0,3 D.1,1
4.一次式M与﹣2x+3y的和是﹣5x+2y,则M等于( )
A.﹣7x+5y B.3x+y C.﹣3x﹣y D.7x﹣5y
5.一次式1﹣y+2x的第二项是 ,第三项的系数是 .
6.一次式中b的系数是 ,常数项是 .
7.若一次式3a+2b﹣1的值为3,那么一次式6a﹣5+4b= .
8.已知(n﹣3)xn﹣1+x﹣2是关于x的一次式,约定x0=1(x≠0),求n的值.
第11讲 一次式(六大题型)
学习目标
1、知道一次式的有关概念 2. 学会合并一次式的同类项; 3、了解一次式的加减及求值、应用等; 4、掌握数与一次式相乘。
一、一次式
代数式5x-3y+4是5.x、-3y和4的和,我们把5x、-3y、4称作代数式5-3y+4的项.
x、-3y只含有一个字母,且字母的指数是1,叫作一次项.不含字母的项叫作常数项,一次项中的数字因数叫作项的数字系数,简称系数.例如,5.x的系数是5,-3y的系数是-3;代数式-x+2y的一次项是一x和2y,一次项的系数分别是一1和2.
【方法规律】x和-x的系数分别是1、一1,而系数 “1”遇常省略不写.
像这样,由一次项与常数项组成,或仅含一次项的代数式叫作一次式.
例-2b、7-、6m+7m、 等都是一次式,但m 、 a-b 、6+3c-c2、-9等都不是一次式.
二、一次式的同类项
一次式5x+3x中的5.x、3x这两项所含字母相同,一次式16S-4S中的16S、-4S这两项所含字母也相同.在一次式中,字母相同的项叫作一次式的同类项,所有常数项都是同类项.
一次式中含字母的同类项可以合并,合并时只要把含字母的同类项的系数相加
一般地,把同类项合并成一项,称为合并同类项.合并一次式的同类项时,把含字母的同类项的系数相加所得的结果作为系数,字母不变;常数项直接相加.
三、一次式的加减
思考:如何计算(2.5x-2)+(3x+8)和(2.5x+8)-(1.5x-3)
数的运算中的去括号方法在一次式中同样适用,即括号前面是“+”号, 去掉括号后,括号内各项都不变;括号前面是“一”号,去掉括号后,括号内各项都变号.
如下所示,根据去括号方法区我们可以分别求出(2.5x-2)+(3x+8)和(2.5x+8)-(1.5x-3)的结果
【方法规律】几个一次式相加减,通常用括号把每个一次式括起来,再用加减号连接。
四、数与一次式相乘
一般地,数与一次式相乘,就是用这个数去乘一次式的每一项,再把所得的积相加.在含有字母的项与数相乘时,把这个数与项的系数相乘的积作为字母的系数,字母不变.运算时要注意这个数与项的系数相乘的积的符号.
【方法规律】 式子2×(5a-2)中问的乘号可以省略不写、简记为2(5a-2).
【即学即练1】 指出一次式5m--8中的一次项、常数项及一次项的系数
【答案】解:一次式5m--8中的一次项是5m和-,常数项是-8,其中
一次项的系数分别是5、-
【即学即练2】指出并合并一次式7m+4n-3-m-6n+5中的同类项.
【答案】解:一次式7m+4n-3-m-6m+5中,7m和-m是同类项,4n和-6n是同类项,-3和5是同类项
因为7m+4n-3-m-6n+5就是7m、4n、-3、-m、-6n、5的和,
所以根据加法的交换律和结合律,得
7m+4n-3-m-6n+5
=7m-m+4n-6n-3+5(加法交换律)
=(7m—m)+(4n-6n)+(-3+5)(加法结合律)
=(7-1)m+(4-6)n+2(合并同类项)
=6m-2n+2.
【即学即练3】先去括号,再合并同类项:
(1)a+2-(9a-3);
(2)—(6m-8)一(-1+2m)。
【答案】 解:(1)a+2—(9a-3)
=a+2-9a+3
=-8a+5.
(2)—(6m-8)-(-1+2m)
= —6m+8+1-2m
=—8m+9.
题型1:一次式的有关概念
【典例1】.指出下列一次式的一次项、常数项和一次项的系数:
(1)6(m-3);
(2)-7(n—3m);
(3)-x+2(3x-2);
(4)3(2x+1)-2(1-x).
【答案】解(1)6(m-3)
=6m+6×(-3)
=6m—18.
(2)—7(n—3m)
=—7n+(-7)×(-3m)
=—7n+21m
(3)-x+2(3x-2)
= -x+6x—4
=5x-4.
(4)3(2x+1)-2(1-x)
=6x+3-2+2x
=8x+1
题型6:一次式有关的图形问题
【典例20】.如图2-3-2,用一根铁丝围成一个长方形,这个长方形的宽是a cm,它的长是(3a-2)cm.如何用一次式表示这根铁丝的长度
【答案】根据题意,铁丝的长为2×(a+3a-2),即2(4a-2)cm
式子2×(4a-2)中问的乘号可以省略不写、简记为2(4a-2).
根据乘法对加法的分配律与乘法结合律,得
2(4a-2)=2×(4a)+2×(-2)(乘法对加法的分配律)
=(2×4)a—4(乘法结合律)
=8a-4.
一、单选题、填空、解答题
1.找出下列代数式中的一次式:
a+3、5-2y 、3x、-9、-、x+y-1.
【答案】略
2.合并同类项:
(1)3m+6m=_______
(2)2m-6m=______;
(3)-2m-6m=_______;
(4)5m+6m=______.
【答案】9m;-4m;-8m;11m
3.判断下列各式是否正确,正确的在括号里打“√”,错误的在括号 里打“×”:
(1)8-6x=2x; ( )
(2)-2y+2y=-4 ( )
(3)3m+4n=7mn; ( )
(4)4m+6m=16m. ( )
【答案】×;×;×;×
4.化简下列一次式:
(1)7m-2-7n+3m;
(2)-5+2m-1
【答案】10m-7n-2;
5.(1)求4x-5与2-y+6x的和;
(2)求5m减去4n-3m+1的差.
【答案】10x-y-3;8m-4n-1
6.先化商,再求值:(2x-y)-(x+y-3),其中x=1,y=-1.
【答案】6
7.计算:
(1)-2(m+6);
(2)-3(n—8);
(3)(-3x+5)×(-5);
(4)(5y-3)×(-3).
【答案】-2m-12;-3n+24;15x-25;-3y+9
8.计算
(1)2(x-3)—5x;
图2-3-1
【答案】解:由图可以知道,正方形地面总面积是16S,蓝色地砖总面积是4S,白色地砖总面积是12S.白色地砖总面积也等于正方形地面总面积减去蓝色地砖总面积,
图2-3-1
由此可以得到
16S-4S=12S,
即16S-4S=(16-4)S
15.甲、乙两车相距130 km,同时出发,相向而行,甲车的速度是80 km/h,乙车的速度是50 km/h.
用一次式表示经过th(t<1)后两车的距离;
经过30 min,两车的距离是多少
【答案】解:
(1)根据题意,经过t/h(t<1)后两车的距离为
(80t+50t)
=130-130t(km).
答:经过th(t<1),两车的距离为(130-130t)km
(2)因为30min=h,时,
有130-130t=130-130×=65(km).
答:经过30 min,两车的距离是65 km
16.中国古代窗花图案设计得简约又美观。如图(1),有一种图案是由 1个小正方形和4个形状相同的小长方形拼成的1个正方形窗花.如果 富花内小正方形的边长为a cm,小长方形的长为b cm,那么如图(2), 由4个这样的窗花做成的正方形窗户的周长是多少
【答案】 8a+8b
17.如图,求涂色部分的周长
【答案】 略
强化训练
1.下列代数式是一次式的是( )
A.8 B.4s+3t C.xy D.
【分析】根据单项式的次数是字母指数的和,多项式的次数是多项式中次数最高的单项式的次数,可得答案.
【解析】解:A、8的次数是0,故A错误;
B、次数是1,故B正确;
C、次数是2,故C错误;
D、是分式,次数是﹣1,故D错误;
故选:B.
2.已知(a﹣1)x3+xb﹣1是关于x的一次式,则a,b的值分别是( )
A.0,3 B.0,1 C.1,2 D.1,1
【分析】根据代数式的定义进行解题即可.
【解析】解:由题可知,a﹣1=0,b﹣1=1,
则a=1,b=2,
故选:C.
3.式子(a﹣1)x3+x(b﹣1)是关于x的一次式,则a、b的值可能为( )
A.0,1 B.1,2 C.0,3 D.1,1
【分析】根据题意得出a﹣1=0,b﹣1≠0,求出a和b的值,再结合给出的选项即可得出答案.
【解析】解:∵多项式(a﹣1)x3+x(b﹣1)是关于x的一次式,
∴a﹣1=0,b﹣1≠0,
∴a=1,b≠1,
∴a、b的值可能为1,2;
故选:B.
4.一次式M与﹣2x+3y的和是﹣5x+2y,则M等于( )
A.﹣7x+5y B.3x+y C.﹣3x﹣y D.7x﹣5y
【分析】本题考查整式的加减运算,解答时合并同类项即可.
根据已知条件可设此多项式为M建立等式解得即可.
【解析】解:M=(﹣5x+2y)﹣(﹣2x+3y)
=﹣5x+2y+2x﹣3y
=﹣3x﹣y
故选:C.
5.一次式1﹣y+2x的第二项是 ﹣y ,第三项的系数是 2 .
【分析】根据多项式的项及单项式的系数的定义求解.
【解析】解:一次式1﹣y+2x是1,﹣y,2x这三个单项式的和,所以第二项是﹣y,第三项2x的系数是2.
故答案为﹣y,2.
6.一次式中b的系数是 ﹣ ,常数项是 1 .
【分析】根据单项式的系数和常数项的定义解答.
【解析】解:一次式中b的系数是﹣,常数项是1.
7.若一次式3a+2b﹣1的值为3,那么一次式6a﹣5+4b= 3 .
【分析】根据题意列出关系式,所求式子变形后将关系式的值代入计算即可求出值.
【解析】解:∵3a+2b﹣1=3,即3a+2b=4,
∴6a﹣5+4b=2(3a+2b)﹣5=8﹣5=3.
故答案为:3
8.已知(n﹣3)xn﹣1+x﹣2是关于x的一次式,约定x0=1(x≠0),求n的值.
【分析】根据一次式的定义得到n﹣1=0或n﹣1=1或n﹣3=0,易求n的值.
【解析】解:∵(n﹣3)xn﹣1+x﹣2是关于x的一次式,约定x0=1(x≠0),
∴n﹣1=0或n﹣1=1或n﹣3=0,
21世纪教育网(www.21cnjy.com)
同课章节目录
