湘教版数学八年级下册(新) 课件:2.5.1 矩形的性质(共18张PPT)
文档属性
| 名称 | 湘教版数学八年级下册(新) 课件:2.5.1 矩形的性质(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 890.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-16 20:46:32 | ||
图片预览



文档简介
课件18张PPT。2.5.1 矩形的性质两组对边分别平行的四边形是平行四边形平行四边形的性质:平行四边形的对边平行;平行四边形的对边相等;平行四边形的对角相等;平行四边形的邻角互补;平行四边形的对角线互相平分;学.科.网
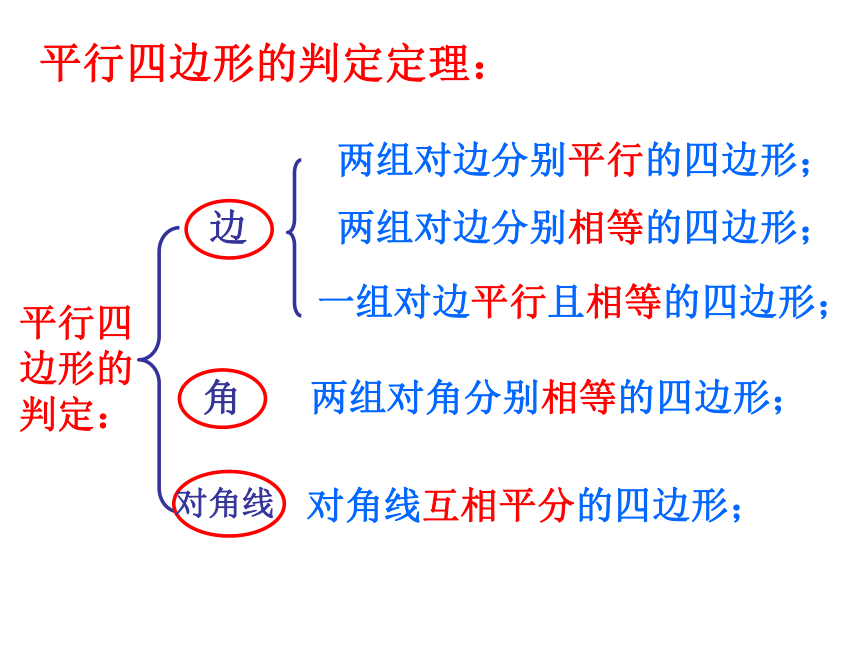
温故知新平行四边形的判定:两组对边分别平行的四边形;两组对边分别相等的四边形;两组对角分别相等的四边形;对角线互相平分的四边形;一组对边平行且相等的四边形;平行四边形的判定定理:情景创设我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质.同样对于平行四边形来说也有特殊的平行四边形,这堂课我们就来研究一种特殊的平行四边形——学.科.网
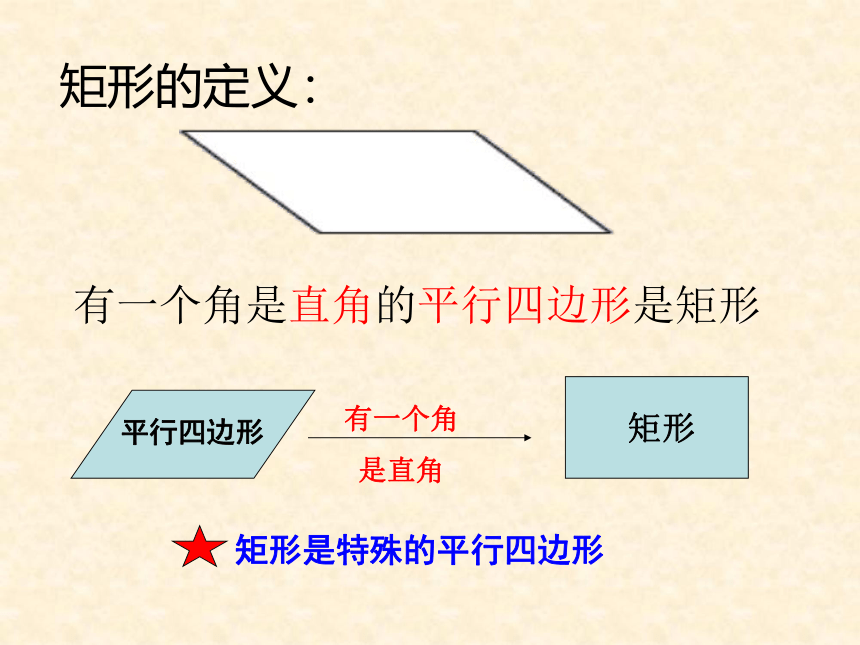
矩形有一个角是直角的平行四边形是矩形矩形的定义:矩形的 两条对角线互相平分学.科.网
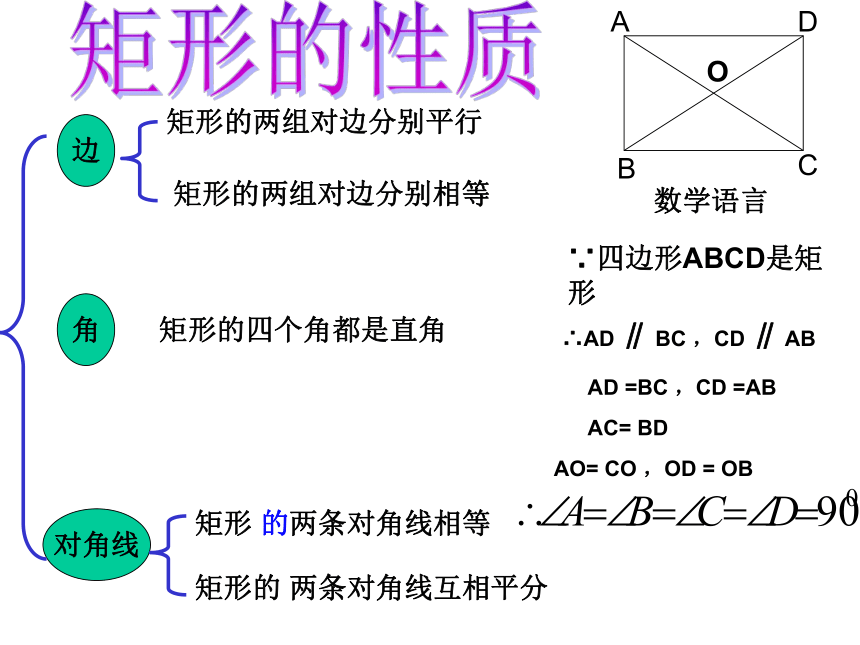
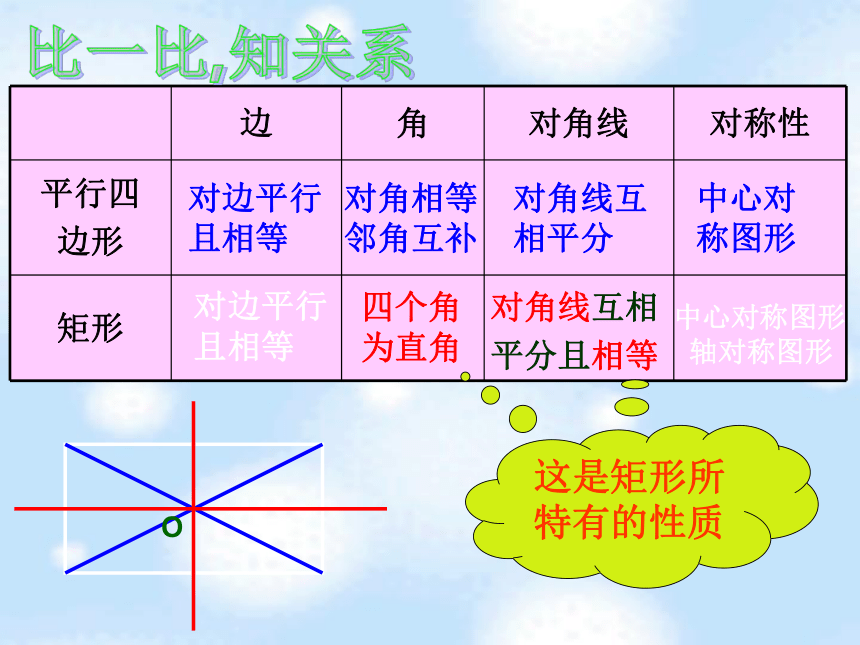
矩形的两组对边分别相等矩形的两组对边分别平行矩形的四个角都是直角矩形 的两条对角线相等边对角线角数学语言∵四边形ABCD是矩形∴AD ∥ BC ,CD ∥ ABAD =BC ,CD =ABAC= BD AO= CO ,OD = OB矩形的性质比一比,知关系对边平行
且相等对角相等
邻角互补对角线互
相平分中心对称图形对边平行
且相等四个角
为直角对角线互相
平分且相等中心对称图形
轴对称图形OODCBA┛在Rt△ABD中,AO是斜边BD的中线直角三角形斜边上中线的性质 :
直角三角形斜边上的中线等于斜边的一半。则有:AO= BD 试试:用文字叙述
直角三角形斜边上中线的性质 在矩形ABCD中
AO=CO=BO=DO= AC= BD例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?∴AC与BD相等且互相平分∴ OA=OB∵ ∠AOB=60°∴ △AOB是等边三角形∴ OA=AB=4(㎝)∴ 矩形的对角线长 AC=BD=2OA=8(㎝)解:∵ 四边形ABCD是矩形已知:如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AC=8cm,求矩形的边长.解:在矩形ABCD中,∵ ∠AOD=120°∴ ∠AOB=60°∵OA=OB∴ △AOB为等边三角形∴AB=OA= AC=4cm在Rt△ABC中,= (cm)BC===方法小结: 如果矩形两对角 线的夹角是60°
或120°, 则其中必有等边三角形. 成长快乐训练营点击进入 矩形具有而一般平行四边形不
具有的性质是 ( ) B.对边相等C营中热身已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm5104营中寻宝3.已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线(1)若BD=3㎝ 则AC= ㎝
(2) 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝.6510营中寻宝
1、矩形具有而平行四边行不具有的的性质是( )
(A)对角相等 (B)对角线相等
(C)对角线互相平分 (D)对边平行且相等
2、矩形的一条对角线与一边的夹角为40°,则两条对角线相交所成的锐角是( )
(A)20° (B)40° (C)60° (D)80°
3、两条直角边的长分别为12和5,则斜边上的中线( )(A)26 (B)13 (C)8。5 (D)6。5
4、已知:如图,矩形ABCD的两条对角线相交于O,∠AOB=60°,AB=4cm,则矩形对角线的长为 cmBDD85、如果矩形的一条对角线的长为8 cm,两条对角线的一个交角为120°,求矩形的边长 6、如图:矩形ABCD的两条对角线
相交于点O,CE‖OB交AB的延长线
于点E,试证明AC与CE的大小关系。
B我的收获从一般到特殊边角对角线矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且平分;
直角三角形斜边上的中线等于斜边的一半. 直角三角形斜边上的中线性质 矩形的定义:
有一个角是直角的平行四边形叫做矩形谢谢!
温故知新平行四边形的判定:两组对边分别平行的四边形;两组对边分别相等的四边形;两组对角分别相等的四边形;对角线互相平分的四边形;一组对边平行且相等的四边形;平行四边形的判定定理:情景创设我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质.同样对于平行四边形来说也有特殊的平行四边形,这堂课我们就来研究一种特殊的平行四边形——学.科.网
矩形有一个角是直角的平行四边形是矩形矩形的定义:矩形的 两条对角线互相平分学.科.网
矩形的两组对边分别相等矩形的两组对边分别平行矩形的四个角都是直角矩形 的两条对角线相等边对角线角数学语言∵四边形ABCD是矩形∴AD ∥ BC ,CD ∥ ABAD =BC ,CD =ABAC= BD AO= CO ,OD = OB矩形的性质比一比,知关系对边平行
且相等对角相等
邻角互补对角线互
相平分中心对称图形对边平行
且相等四个角
为直角对角线互相
平分且相等中心对称图形
轴对称图形OODCBA┛在Rt△ABD中,AO是斜边BD的中线直角三角形斜边上中线的性质 :
直角三角形斜边上的中线等于斜边的一半。则有:AO= BD 试试:用文字叙述
直角三角形斜边上中线的性质 在矩形ABCD中
AO=CO=BO=DO= AC= BD例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?∴AC与BD相等且互相平分∴ OA=OB∵ ∠AOB=60°∴ △AOB是等边三角形∴ OA=AB=4(㎝)∴ 矩形的对角线长 AC=BD=2OA=8(㎝)解:∵ 四边形ABCD是矩形已知:如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AC=8cm,求矩形的边长.解:在矩形ABCD中,∵ ∠AOD=120°∴ ∠AOB=60°∵OA=OB∴ △AOB为等边三角形∴AB=OA= AC=4cm在Rt△ABC中,= (cm)BC===方法小结: 如果矩形两对角 线的夹角是60°
或120°, 则其中必有等边三角形. 成长快乐训练营点击进入 矩形具有而一般平行四边形不
具有的性质是 ( ) B.对边相等C营中热身已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm5104营中寻宝3.已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线(1)若BD=3㎝ 则AC= ㎝
(2) 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝.6510营中寻宝
1、矩形具有而平行四边行不具有的的性质是( )
(A)对角相等 (B)对角线相等
(C)对角线互相平分 (D)对边平行且相等
2、矩形的一条对角线与一边的夹角为40°,则两条对角线相交所成的锐角是( )
(A)20° (B)40° (C)60° (D)80°
3、两条直角边的长分别为12和5,则斜边上的中线( )(A)26 (B)13 (C)8。5 (D)6。5
4、已知:如图,矩形ABCD的两条对角线相交于O,∠AOB=60°,AB=4cm,则矩形对角线的长为 cmBDD85、如果矩形的一条对角线的长为8 cm,两条对角线的一个交角为120°,求矩形的边长 6、如图:矩形ABCD的两条对角线
相交于点O,CE‖OB交AB的延长线
于点E,试证明AC与CE的大小关系。
B我的收获从一般到特殊边角对角线矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且平分;
直角三角形斜边上的中线等于斜边的一半. 直角三角形斜边上的中线性质 矩形的定义:
有一个角是直角的平行四边形叫做矩形谢谢!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
