22.2 相似三角形的判定教学课件
图片预览





文档简介
课件17张PPT。相似三角形的判定(一)九(12)班
执教:张明敏
一.复习引入 什么样的两个多边形是相似多边形?
两个边数相同的多边形,如果它们的对应角相等,对应边长度的比相等 ,那么这两个多边形叫做相似多边形.
相似多边形对应边长度的比叫做相似比或相似系数.二.讲授新课△ABC∽△A′B′C′(顶点要对应)∵△ABC∽△A′B′C′
∴∠A=∠A′,∠B=∠B′,∠C=∠C′,
(2)相似三角形的表示
对应角相等,对应边成比例的三角形
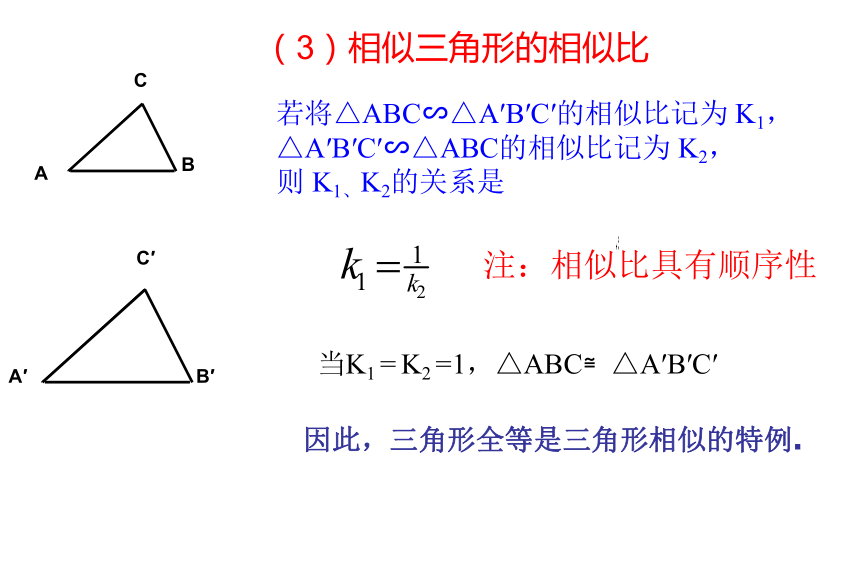
叫做相似三角形(1)相似三角形的定义相似三角形对应边、对应角的关系:(3)相似三角形的相似比 因此,三角形全等是三角形相似的特例.注:相似比具有顺序性
若将△ABC∽△A′B′C′的相似比记为 K1,
△A′B′C′∽△ABC的相似比记为 K2,
则 K1、K2的关系是
当K1 = K2 =1,△ABC≌△A′B′C′三.探究论证 (1) 在△ABC中,DE ∥ BC,
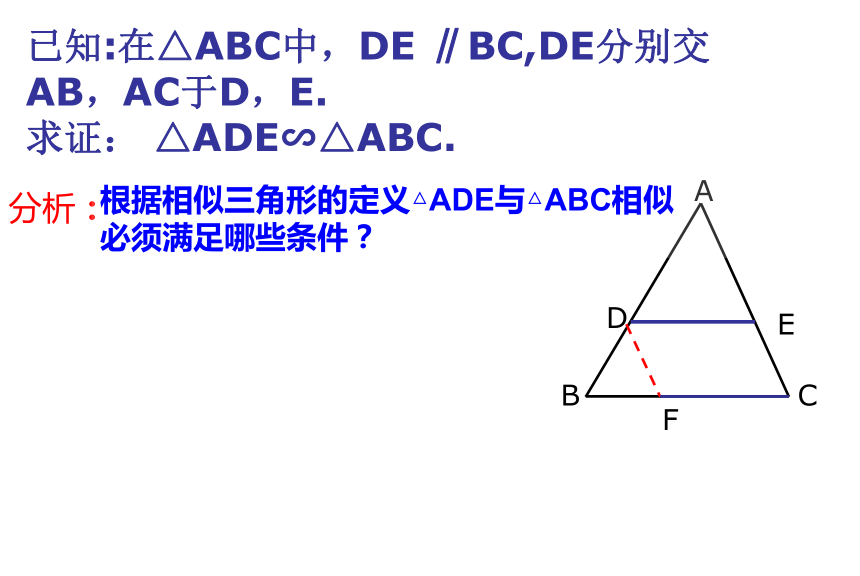
你能得到哪些比例线段?ABCED(2)F分析:ADEBCF根据相似三角形的定义△ADE与△ABC相似 必须满足哪些条件?已知:在△ABC中,DE ∥BC,DE分别交AB,AC于D,E.
求证: △ADE∽△ABC. 如图2、图3所示, 如果这条直线与三角形两边的延长线相交,△ADE与△ABC还相似吗?
图1图2图3辅助线旋转四.定理归纳图3符号语言: 在△ABC中 ∵DE∥BC
∴△ADE∽△ABC.
图2图1相似1、如图4,在平行四边形ABCD中,D交BC于F,交AB的延长线于点E.
请写出图中所有的相似的三角形;1. AD∥BF2.BE∥CD△EDA∽△DFC△FBE∽△FCD△EFB∽△EDA,三角形相似具有传递性!五.练习巩固成立的有(1) (2) (4)
相似三角形判定方法1、对应角相等,三组对应边的比也相等的两个三角形是相似三角形.2、(重要结论)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似. 与同桌交流一下你这节课的收获! 六.课堂小结七.作业设计
1.基础训练22.2(一)
2.补充练习:如图5,△ABC
中BD是角平分线,过点D作
DE∥AB交BC于E,AB=5cm
, BE=3cm,求EC的长.2、如图,在△ABC中,∠C的平分
线交AB于D,过点D作DE∥BC交
AC于E,若AD:DB=4:3,则EC:BC=______。4:71、如右图,在△ABC中,DE∥BC,
则 △ADE∽ ______,
∠ADE=______,∠ AED= ______,
=________ 如果A E=3cm,EC=2cm,则
△ADE与△ABC的相似比为______ △ABC ∠B∠C 3:5
谢谢大家!相似三角形判定方法1、对应角相等,三组对应边的比也相等的两个三角形是相似三角形.2、(重要结论)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似. 与同桌交流一下你这节课的收获! 六.课堂小结3.如图,AC⊥BC于点C,DE⊥AC于点E.
若DE=10,BC=30,BD=8,
求AB的长.本题数据不合理 如图:AB是斜靠在墙上的长梯,梯脚B距墙80cm,梯上点D距墙70cm,BD长55cm,你可以计算出梯的长度吗?
执教:张明敏
一.复习引入 什么样的两个多边形是相似多边形?
两个边数相同的多边形,如果它们的对应角相等,对应边长度的比相等 ,那么这两个多边形叫做相似多边形.
相似多边形对应边长度的比叫做相似比或相似系数.二.讲授新课△ABC∽△A′B′C′(顶点要对应)∵△ABC∽△A′B′C′
∴∠A=∠A′,∠B=∠B′,∠C=∠C′,
(2)相似三角形的表示
对应角相等,对应边成比例的三角形
叫做相似三角形(1)相似三角形的定义相似三角形对应边、对应角的关系:(3)相似三角形的相似比 因此,三角形全等是三角形相似的特例.注:相似比具有顺序性
若将△ABC∽△A′B′C′的相似比记为 K1,
△A′B′C′∽△ABC的相似比记为 K2,
则 K1、K2的关系是
当K1 = K2 =1,△ABC≌△A′B′C′三.探究论证 (1) 在△ABC中,DE ∥ BC,
你能得到哪些比例线段?ABCED(2)F分析:ADEBCF根据相似三角形的定义△ADE与△ABC相似 必须满足哪些条件?已知:在△ABC中,DE ∥BC,DE分别交AB,AC于D,E.
求证: △ADE∽△ABC. 如图2、图3所示, 如果这条直线与三角形两边的延长线相交,△ADE与△ABC还相似吗?
图1图2图3辅助线旋转四.定理归纳图3符号语言: 在△ABC中 ∵DE∥BC
∴△ADE∽△ABC.
图2图1相似1、如图4,在平行四边形ABCD中,D交BC于F,交AB的延长线于点E.
请写出图中所有的相似的三角形;1. AD∥BF2.BE∥CD△EDA∽△DFC△FBE∽△FCD△EFB∽△EDA,三角形相似具有传递性!五.练习巩固成立的有(1) (2) (4)
相似三角形判定方法1、对应角相等,三组对应边的比也相等的两个三角形是相似三角形.2、(重要结论)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似. 与同桌交流一下你这节课的收获! 六.课堂小结七.作业设计
1.基础训练22.2(一)
2.补充练习:如图5,△ABC
中BD是角平分线,过点D作
DE∥AB交BC于E,AB=5cm
, BE=3cm,求EC的长.2、如图,在△ABC中,∠C的平分
线交AB于D,过点D作DE∥BC交
AC于E,若AD:DB=4:3,则EC:BC=______。4:71、如右图,在△ABC中,DE∥BC,
则 △ADE∽ ______,
∠ADE=______,∠ AED= ______,
=________ 如果A E=3cm,EC=2cm,则
△ADE与△ABC的相似比为______ △ABC ∠B∠C 3:5
谢谢大家!相似三角形判定方法1、对应角相等,三组对应边的比也相等的两个三角形是相似三角形.2、(重要结论)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似. 与同桌交流一下你这节课的收获! 六.课堂小结3.如图,AC⊥BC于点C,DE⊥AC于点E.
若DE=10,BC=30,BD=8,
求AB的长.本题数据不合理 如图:AB是斜靠在墙上的长梯,梯脚B距墙80cm,梯上点D距墙70cm,BD长55cm,你可以计算出梯的长度吗?
