23.2 解直角三角形及其应用教学课件
文档属性
| 名称 | 23.2 解直角三角形及其应用教学课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 269.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-17 00:00:00 | ||
图片预览

文档简介
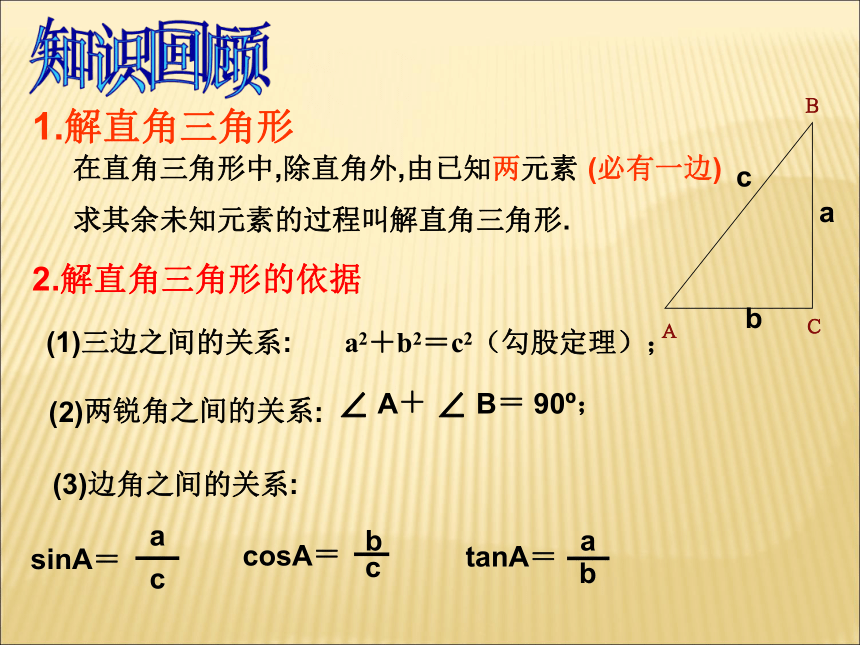
课件10张PPT。23.2解直角三角形及其应用(2)九(3)是我家 我爱我家在直角三角形中,除直角外,由已知两元素
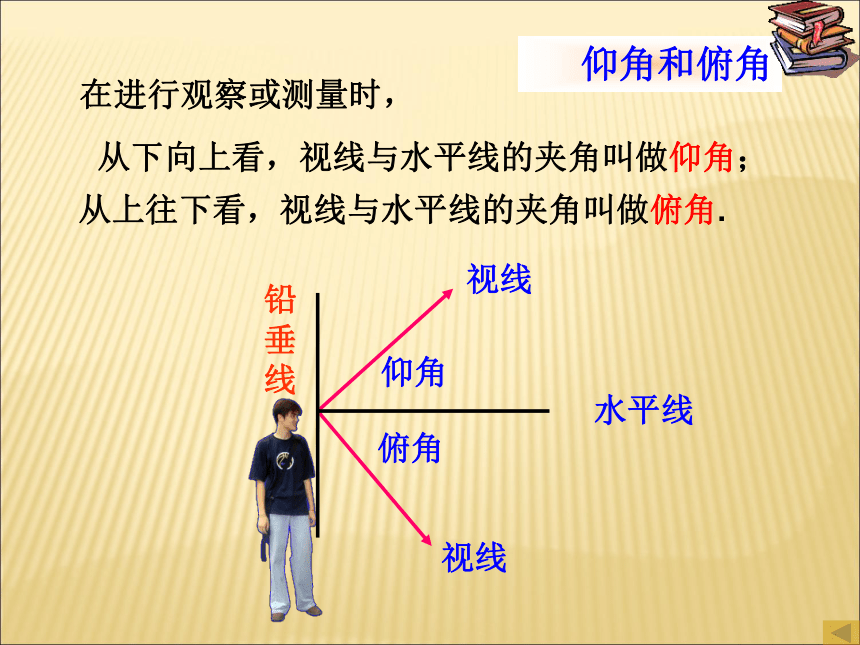
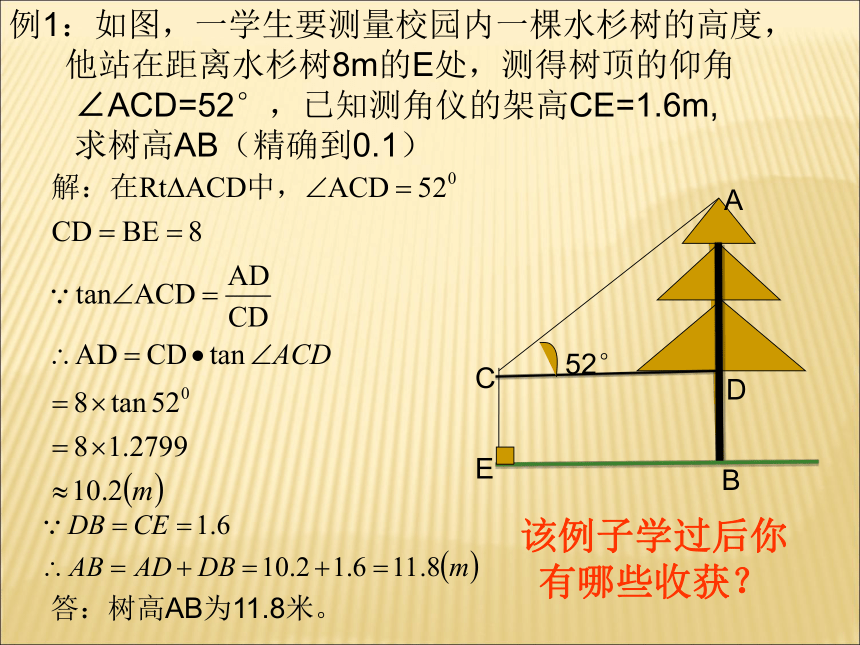
求其余未知元素的过程叫解直角三角形.1.解直角三角形(1)三边之间的关系:a2+b2=c2(勾股定理);2.解直角三角形的依据(2)两锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:sinA=知识回顾(必有一边)视线视线仰角俯角在进行观察或测量时,从上往下看,视线与水平线的夹角叫做俯角.从下向上看,视线与水平线的夹角叫做仰角;例1:如图,一学生要测量校园内一棵水杉树的高度,
他站在距离水杉树8m的E处,测得树顶的仰角
∠ACD=52°,已知测角仪的架高CE=1.6m,
求树高AB(精确到0.1)答:树高AB为11.8米。该例子学过后你
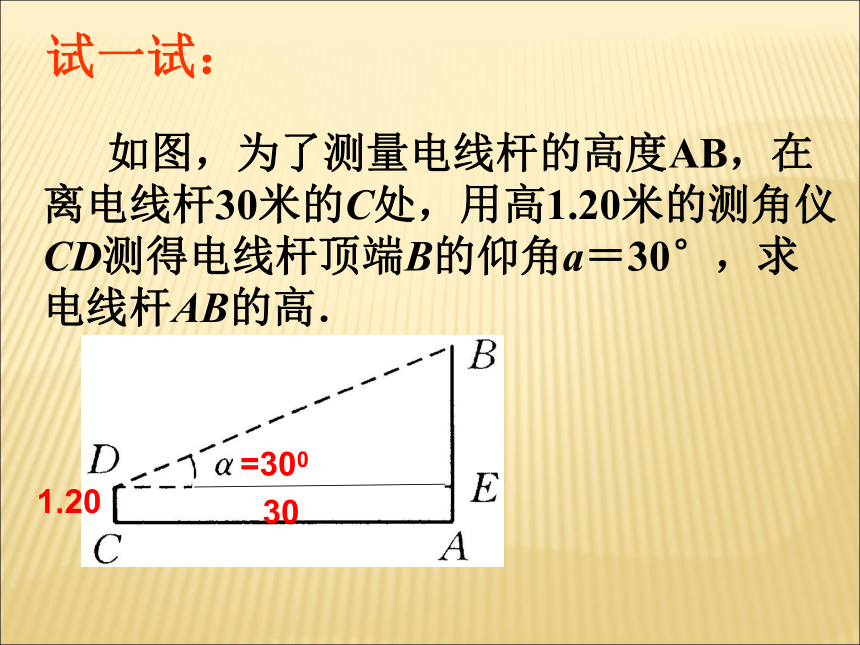
有哪些收获? 如图,为了测量电线杆的高度AB,在离电线杆30米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=30°,求电线杆AB的高.试一试:例2:如图,某校九年级学生为了测量当地电视塔高度AB,
因为不能直接到达塔底B处,他们采用在发射台院外
与电视塔底B成一直线的C,D两处地面上,用测角器
测得电视塔顶部A的仰角分别为45°和30°,同时量得
CD=50m,已知测角器高为1m,由此求电视塔的高
为多少米?(精确到1m)xmxm答:电视塔的高69 米。 1.如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=300,求飞机A到控制点B的距离.2. 两座建筑AB及CD,其地面距离AC为50米,从AB的顶点B测得CD的顶部D的仰角β=300,测得其底部C的俯角a=600, 求两座建筑物AB及CD的高.120050米30°60°1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。2、一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。善于总结是学习的前提条件课堂作业:P131习题23.2第2,3,4题课外作业:基础训练P107
基础练习23.2(2)
求其余未知元素的过程叫解直角三角形.1.解直角三角形(1)三边之间的关系:a2+b2=c2(勾股定理);2.解直角三角形的依据(2)两锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:sinA=知识回顾(必有一边)视线视线仰角俯角在进行观察或测量时,从上往下看,视线与水平线的夹角叫做俯角.从下向上看,视线与水平线的夹角叫做仰角;例1:如图,一学生要测量校园内一棵水杉树的高度,
他站在距离水杉树8m的E处,测得树顶的仰角
∠ACD=52°,已知测角仪的架高CE=1.6m,
求树高AB(精确到0.1)答:树高AB为11.8米。该例子学过后你
有哪些收获? 如图,为了测量电线杆的高度AB,在离电线杆30米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=30°,求电线杆AB的高.试一试:例2:如图,某校九年级学生为了测量当地电视塔高度AB,
因为不能直接到达塔底B处,他们采用在发射台院外
与电视塔底B成一直线的C,D两处地面上,用测角器
测得电视塔顶部A的仰角分别为45°和30°,同时量得
CD=50m,已知测角器高为1m,由此求电视塔的高
为多少米?(精确到1m)xmxm答:电视塔的高69 米。 1.如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=300,求飞机A到控制点B的距离.2. 两座建筑AB及CD,其地面距离AC为50米,从AB的顶点B测得CD的顶部D的仰角β=300,测得其底部C的俯角a=600, 求两座建筑物AB及CD的高.120050米30°60°1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。2、一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。善于总结是学习的前提条件课堂作业:P131习题23.2第2,3,4题课外作业:基础训练P107
基础练习23.2(2)
