23.2 解直角三角形及其应用课件
图片预览



文档简介
课件13张PPT。欢迎各位领导、老师莅临指导!固镇县实验中学 陈红梅23.2解直角三角形及其应用1. 什 么叫 解 直 角 三 角 形?
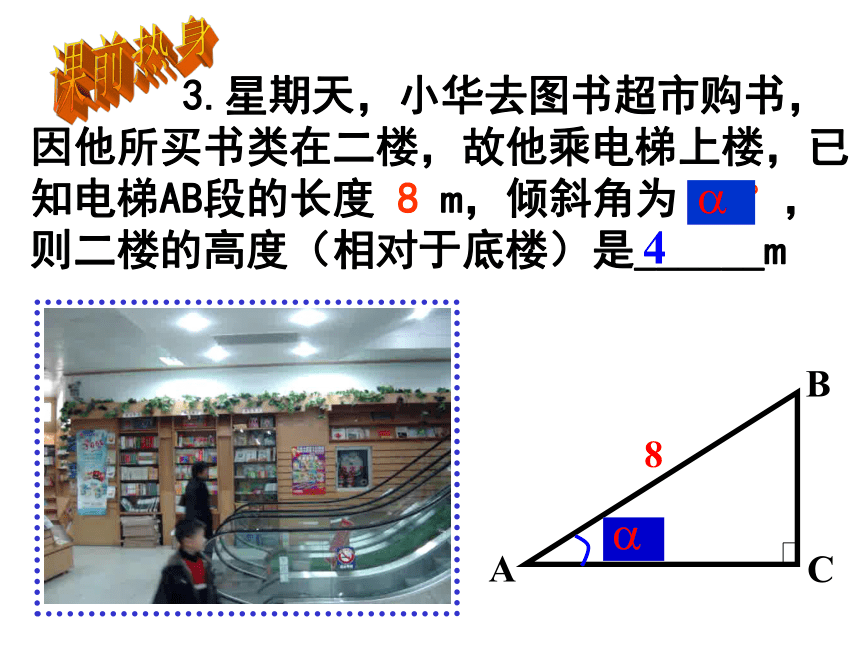
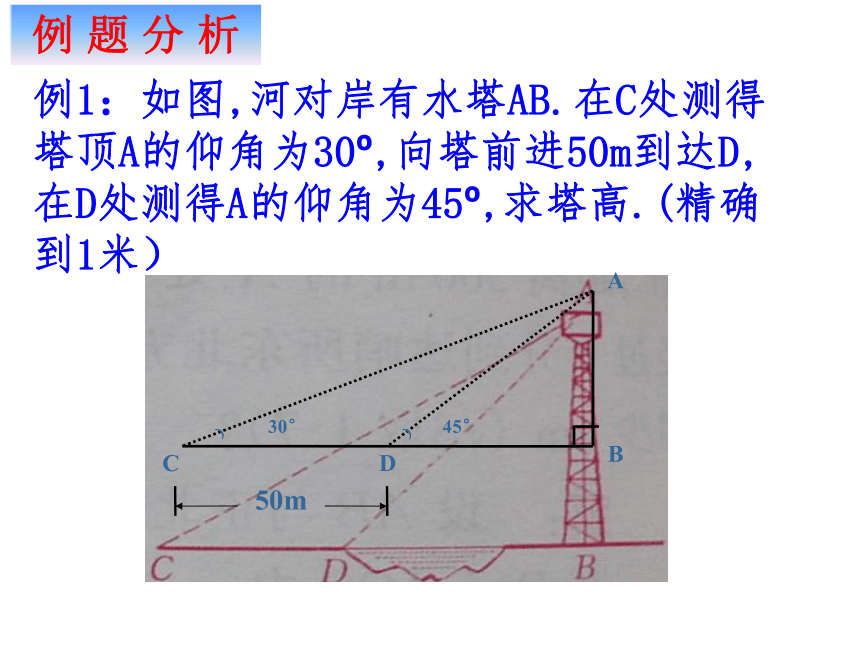
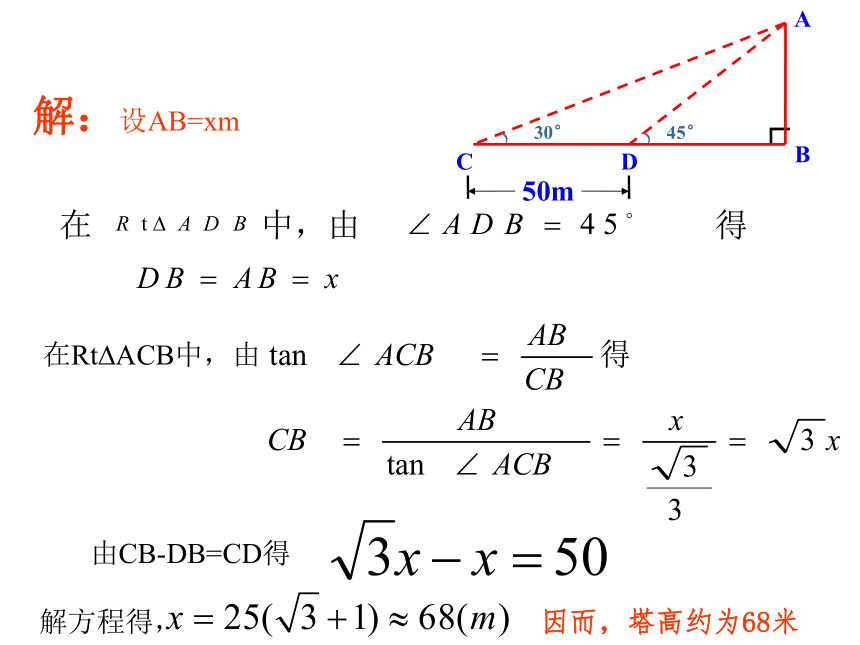
解直角三角形有那几种类型?2.特殊角三角函数值是什么?课前热身 3.星期天,小华去图书超市购书,因他所买书类在二楼,故他乘电梯上楼,已知电梯AB段的长度 8 m,倾斜角为 30°,则二楼的高度(相对于底楼)是______m4课前热身例1:如图,河对岸有水塔AB.在C处测得塔顶A的仰角为30o,向塔前进50m到达D,在D处测得A的仰角为45o,求塔高.(精确到1米) 例 题 分 析在 中,由 得解方程得,因而,塔高约为68米解:设AB=xm在Rt?ACB中,由由CB-DB=CD得 A 和 B 两名测量员站在同一个水平地面上观测悬崖顶。由 A 测得悬崖顶的仰角是 30o,而由 B 测得悬崖頂顶的仰角是 45o,若 A、B 及崖底 D 成一直线及 A 和 B 相距 100m,求悬崖的高度。 练 习CADBNN130?60? 例 题 解 析1hX
例2:如图,海岛C四周10n mile周围内为暗礁区,一艘货轮以20n mile/h的速度由东向西航行,在A处见岛C在北偏西60?,航行1h到达B,见岛C在北偏西30?,货轮继续向西航行,有无触礁的危险?30?60?解:由点C作AB的垂线交AB的延长线于点D,垂足为D,∠CDB=90°设CD=X,在Rt△BCD中由在Rt△ACD中,由所以没有触礁危险得:由AD-BD=AB得 海中有一个小岛A,它的周围8海里内有暗礁,渔船跟踪鱼群由西向到航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏到30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险? 练 习AD60°300BADF解:由点A作BD的垂线交BD的延长线于点F,垂足为F,∠AFD=90°设AF= x在Rt△ADF中,在Rt△ABF中,所以没有触礁危险30°60°解得x=x这节课你有哪些收获?1 、将实际问题转化为数学模型
--解直角三角形的问题2、体会到数学与生活紧密联系,生活离不开数学3、解直角三角形时灵活应用方程思想方法。布置作业:1、P128练习 第1题
2、P132习题23.2 第7题 成功就是99%的汗水,加上1%的灵感。
------爱迪生 在科学上从没有平坦的大道,只有不畏艰险勇于攀登的人,才能达到光辉的顶点
马克思
例2:如图,海岛C四周10n mile周围内为暗礁区,一艘货轮以20n mile/h的速度由东向西航行,在A处见岛C在北偏西60?,航行1h到达B,见岛C在北偏西30?,货轮继续向西航行,有无触礁的危险?30?60?解:由点C作AB的垂线交AB的延长线于点D,垂足为D,∠CDB=90°设CD=X,在Rt△BCD中由在Rt△ACD中,由所以没有触礁危险得:由AD-BD=AB得 海中有一个小岛A,它的周围8海里内有暗礁,渔船跟踪鱼群由西向到航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏到30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险? 练 习AD60°300BADF解:由点A作BD的垂线交BD的延长线于点F,垂足为F,∠AFD=90°设AF= x在Rt△ADF中,在Rt△ABF中,所以没有触礁危险30°60°解得x=x这节课你有哪些收获?1 、将实际问题转化为数学模型
--解直角三角形的问题2、体会到数学与生活紧密联系,生活离不开数学3、解直角三角形时灵活应用方程思想方法。布置作业:1、P128练习 第1题
2、P132习题23.2 第7题 成功就是99%的汗水,加上1%的灵感。
------爱迪生 在科学上从没有平坦的大道,只有不畏艰险勇于攀登的人,才能达到光辉的顶点
马克思
