23.2解直角三角形及其应用 课件
图片预览




文档简介
课件16张PPT。九年级(1)班任课教师:段礼胜教书育人,为人师表1、了解仰角和俯角的概念; 并能用直角三角形的知识解决实际问题。
2、将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题。
3、掌握数学建模的思想,体会数学源于生活,服务于生活,提高数学应用意识。
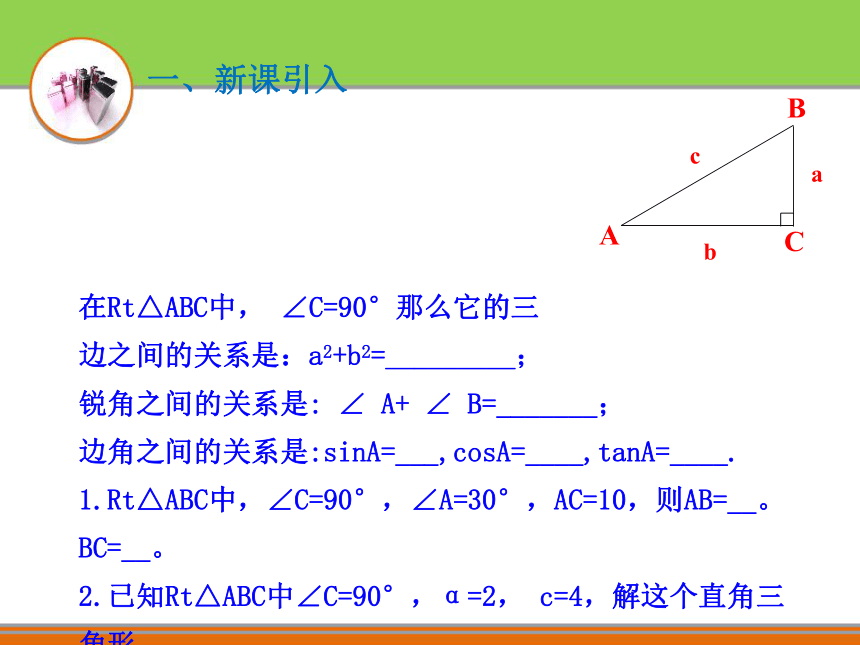
4、培养学生自主探究与合作交流的学习习惯。教学目标一、新课引入 1、讲解
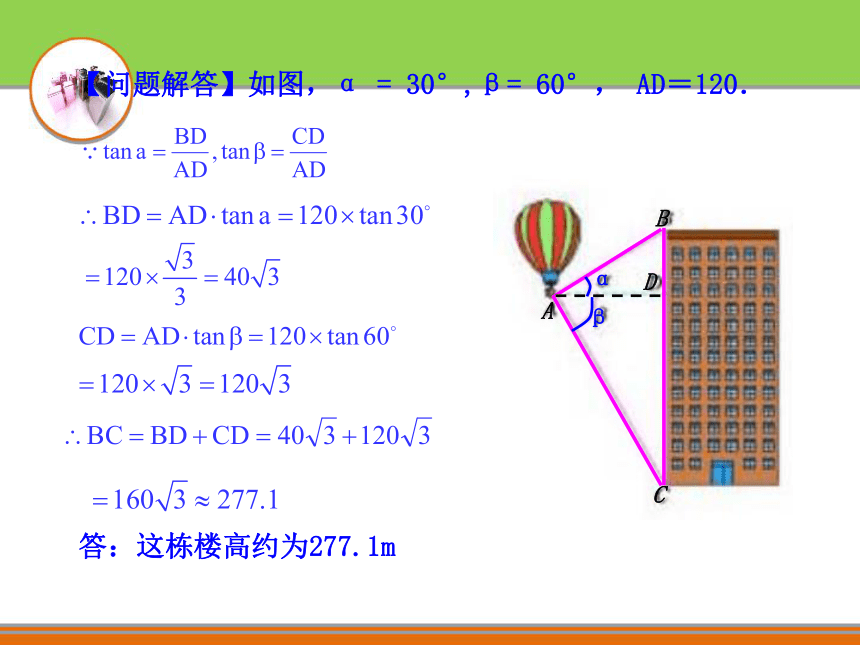
仰角、俯角的概念二、共同探究 在视线与水平线所成的角中,视线在水平线上方的叫做仰角。视线在水平面下方的叫俯角。 如图:热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m)【合作探究】Rt△ABC中,α=30°,
AD=120,所以利用解直角三
角形的知识求出BD;类似地
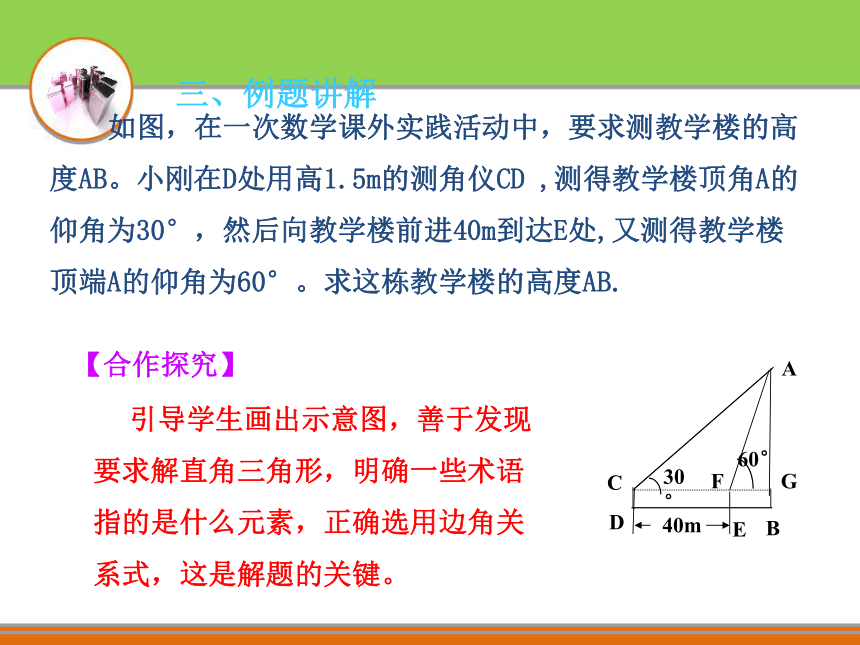
可以求出CD,进而求出BC.2、练习新知【问题解答】如图,α = 30°,β= 60°, AD=120.答:这栋楼高约为277.1m 如图,在一次数学课外实践活动中,要求测教学楼的高度AB。小刚在D处用高1.5m的测角仪CD ,测得教学楼顶角A的仰角为30°,然后向教学楼前进40m到达E处,又测得教学楼顶端A的仰角为60°。求这栋教学楼的高度AB.
【合作探究】 引导学生画出示意图,善于发现要求解直角三角形,明确一些术语指的是什么元素,正确选用边角关系式,这是解题的关键。三、例题讲解【问题解答】如图,由题意可知, ∠ACG=30°,∠AFG=60°, CF=DE=40m,设AG=xm在Rt⊿AFG中,FG= ,
在Rt⊿ACG中,CG= ,
∵CF=CG-FG
∴ - =40
∴x=20
∵BG=CD=1.5, AB=AG+GB
∴AB=(20 +1.5)
所以,教学楼高AB为(20 +1.5)m
1. 为了缓解市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图)已知立杆AB高度是3米,从侧面点D测得显示牌顶端点C和低端点B的仰角分别为60°和45°,求路况显示牌BC的高度。(结果保留根号)
四、巩固提高【自主解答】在等腰三角形BDA中∵∠BAD=90°,∠ADB=45°
∴AD=AB=3m
在Rt△ACD中,∵∠ADC=60°
∴AC=tan∠ADC×AD=tan60°×3
=3
所以BC=AC-AB=( 3 -3)m
答:路况显示牌BC的高度为 (3 -3)m. 2、某岛屿的最高峰的海拔高度约360m,如图,飞机在岛屿上空巡逻时沿水平方向(A,B两点所在直线)飞行,飞行高度为1000m,飞行中在A,B两点测得岛屿的最高峰C的俯角分别为30°、45°,求飞行距离AB的长。(参考数据: =1.7) 【小组讨论】【答案:AB约为448m 】 用解直角三角形的知识解决实际问题的一般步骤:
(1)审题、绘图,弄清已知和未知;
(2)通过作辅助线产生有关的直角三角形,把问题转化为解直角三角形的问题;
(3)根据直角三角形元素(边、角)之间的关系解有关的直角三角形.六、小结与评价板书设计第2课时 解直角三角形的应用(2)
当我们测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角;在水平线下方的角叫做俯角。课后作业:1、在高出海平面100米的山岩上有一点A ,看到一艘船B的俯角为30°,则船与山脚的水平面的距离为 2、王师傅在楼顶上的点A处测得楼前一棵树CD的顶端C的俯角为60°,已知水平距离BD=10米,楼高AB=24米,则树CD的高度为(100 )米(24-10 )米3、如图在电线杆离地面6米高的C处向地面拉缆绳,缆绳和地面成63°的角,求缆绳AC的长。(精确到0.01米)
〖答案〗6.73米答:大楼的高度CD约为116米.
2、将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题。
3、掌握数学建模的思想,体会数学源于生活,服务于生活,提高数学应用意识。
4、培养学生自主探究与合作交流的学习习惯。教学目标一、新课引入 1、讲解
仰角、俯角的概念二、共同探究 在视线与水平线所成的角中,视线在水平线上方的叫做仰角。视线在水平面下方的叫俯角。 如图:热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m)【合作探究】Rt△ABC中,α=30°,
AD=120,所以利用解直角三
角形的知识求出BD;类似地
可以求出CD,进而求出BC.2、练习新知【问题解答】如图,α = 30°,β= 60°, AD=120.答:这栋楼高约为277.1m 如图,在一次数学课外实践活动中,要求测教学楼的高度AB。小刚在D处用高1.5m的测角仪CD ,测得教学楼顶角A的仰角为30°,然后向教学楼前进40m到达E处,又测得教学楼顶端A的仰角为60°。求这栋教学楼的高度AB.
【合作探究】 引导学生画出示意图,善于发现要求解直角三角形,明确一些术语指的是什么元素,正确选用边角关系式,这是解题的关键。三、例题讲解【问题解答】如图,由题意可知, ∠ACG=30°,∠AFG=60°, CF=DE=40m,设AG=xm在Rt⊿AFG中,FG= ,
在Rt⊿ACG中,CG= ,
∵CF=CG-FG
∴ - =40
∴x=20
∵BG=CD=1.5, AB=AG+GB
∴AB=(20 +1.5)
所以,教学楼高AB为(20 +1.5)m
1. 为了缓解市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图)已知立杆AB高度是3米,从侧面点D测得显示牌顶端点C和低端点B的仰角分别为60°和45°,求路况显示牌BC的高度。(结果保留根号)
四、巩固提高【自主解答】在等腰三角形BDA中∵∠BAD=90°,∠ADB=45°
∴AD=AB=3m
在Rt△ACD中,∵∠ADC=60°
∴AC=tan∠ADC×AD=tan60°×3
=3
所以BC=AC-AB=( 3 -3)m
答:路况显示牌BC的高度为 (3 -3)m. 2、某岛屿的最高峰的海拔高度约360m,如图,飞机在岛屿上空巡逻时沿水平方向(A,B两点所在直线)飞行,飞行高度为1000m,飞行中在A,B两点测得岛屿的最高峰C的俯角分别为30°、45°,求飞行距离AB的长。(参考数据: =1.7) 【小组讨论】【答案:AB约为448m 】 用解直角三角形的知识解决实际问题的一般步骤:
(1)审题、绘图,弄清已知和未知;
(2)通过作辅助线产生有关的直角三角形,把问题转化为解直角三角形的问题;
(3)根据直角三角形元素(边、角)之间的关系解有关的直角三角形.六、小结与评价板书设计第2课时 解直角三角形的应用(2)
当我们测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角;在水平线下方的角叫做俯角。课后作业:1、在高出海平面100米的山岩上有一点A ,看到一艘船B的俯角为30°,则船与山脚的水平面的距离为 2、王师傅在楼顶上的点A处测得楼前一棵树CD的顶端C的俯角为60°,已知水平距离BD=10米,楼高AB=24米,则树CD的高度为(100 )米(24-10 )米3、如图在电线杆离地面6米高的C处向地面拉缆绳,缆绳和地面成63°的角,求缆绳AC的长。(精确到0.01米)
〖答案〗6.73米答:大楼的高度CD约为116米.
