青岛版(六三制)数学八年级上册 第2章 图形的轴对称 复习课件(共47张PPT)
文档属性
| 名称 | 青岛版(六三制)数学八年级上册 第2章 图形的轴对称 复习课件(共47张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 590.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-08 08:25:09 | ||
图片预览


文档简介
(共47张PPT)
第2的轴对称
复习课件
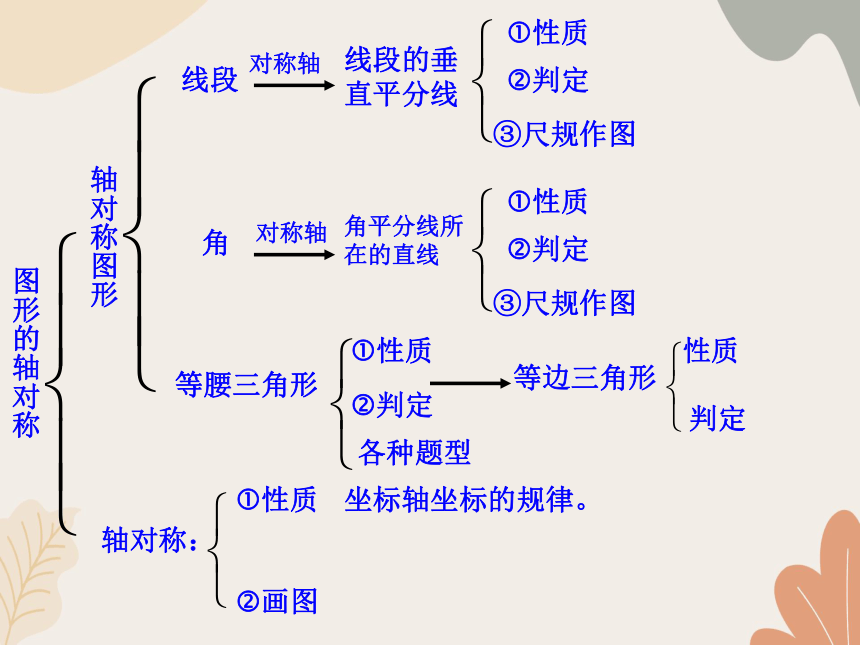
图形的轴对称
轴对称:
线段
角
等腰三角形
对称轴
线段的垂直平分线
性质
③尺规作图
性质
画图
各种题型
等边三角形
性质
判定
轴对称图形
判定
对称轴
角平分线所在的直线
性质
③尺规作图
判定
性质
判定
坐标轴坐标的规律。
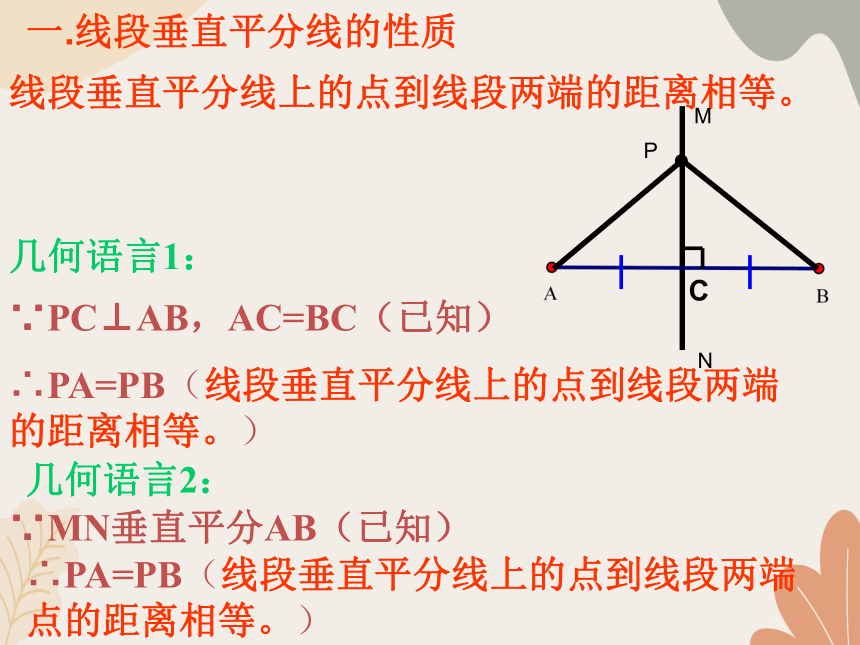
一.线段垂直平分线的性质
线段垂直平分线上的点到线段两端的距离相等。
M
N
P
C
几何语言1:
∵PC⊥AB,AC=BC(已知)
∴PA=PB(线段垂直平分线上的点到线段两端的距离相等。)
几何语言2:
∵MN垂直平分AB(已知)
∴PA=PB(线段垂直平分线上的点到线段两端点的距离相等。)
例1已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P。
求证:PA=PB=PC
证明:
∵MN垂直平分AB
∴PA=PB
同理PB=PC
∴PA=PB=PC
B
A
C
M
N
M′
N′
P
B
A
C
M
N
M′
N′
P
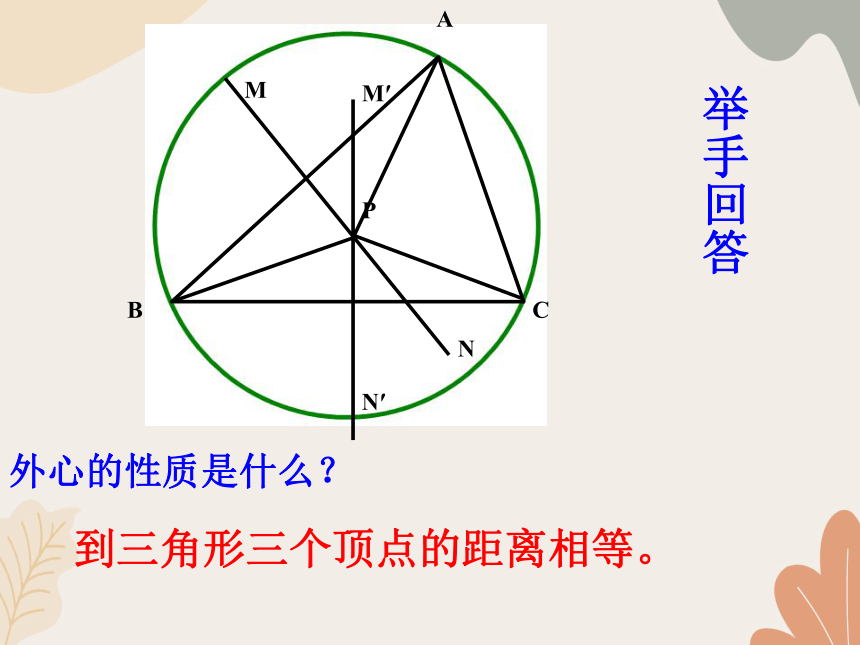
外心的性质是什么?
到三角形三个顶点的距离相等。
举手回答
B
A
C
M
N
M′
N′
P
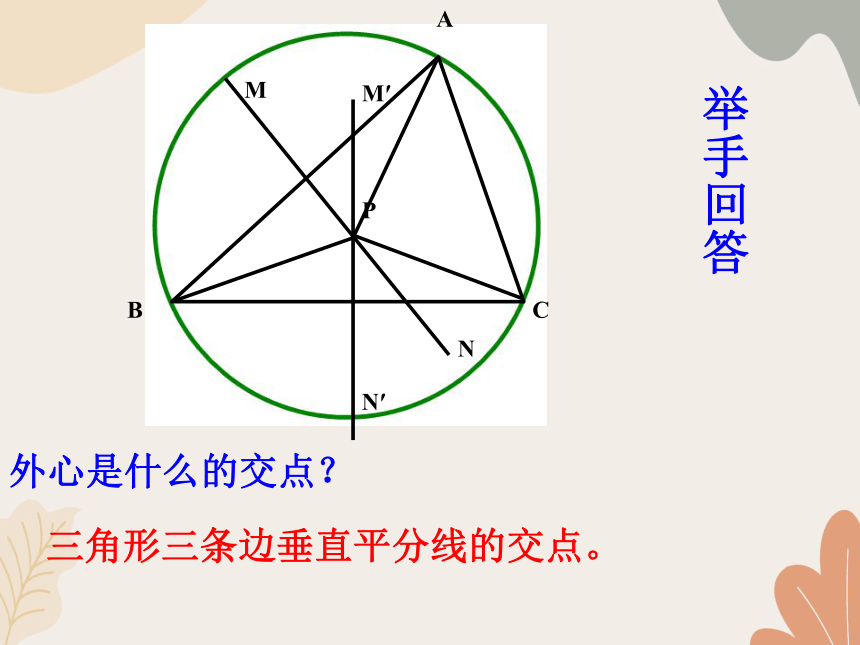
外心是什么的交点?
三角形三条边垂直平分线的交点。
举手回答
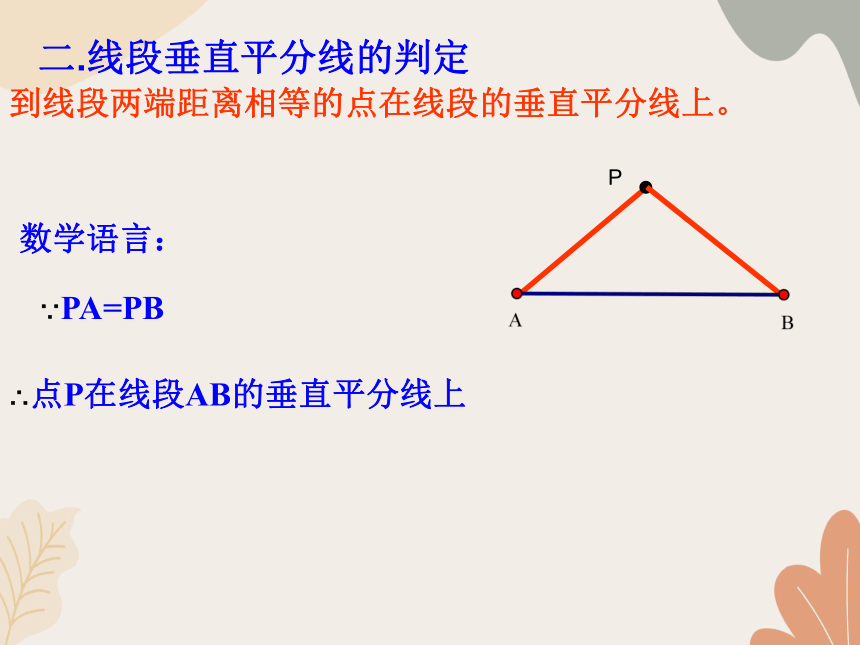
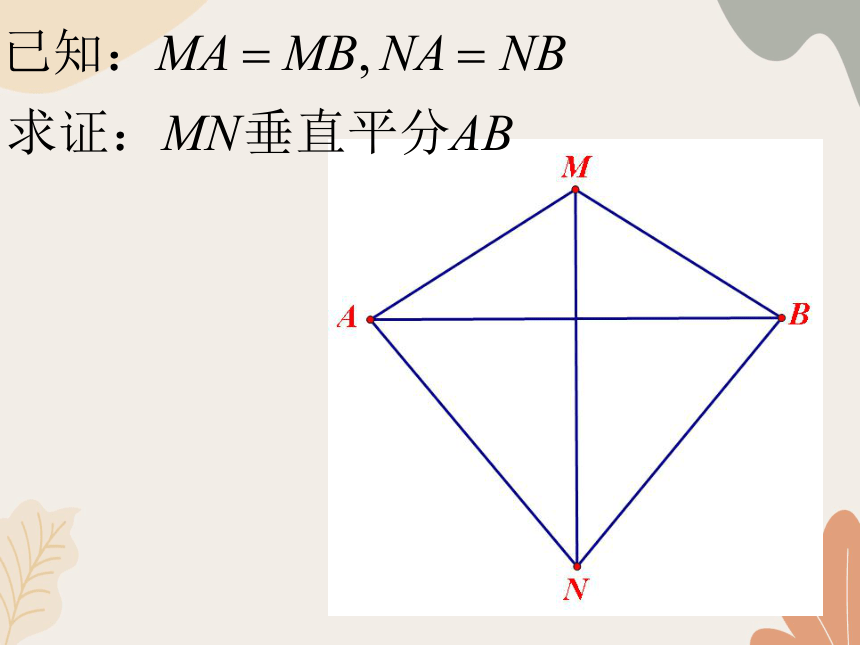
到线段两端距离相等的点在线段的垂直平分线上。
P
∵PA=PB
∴点P在线段AB的垂直平分线上
二.线段垂直平分线的判定
数学语言:
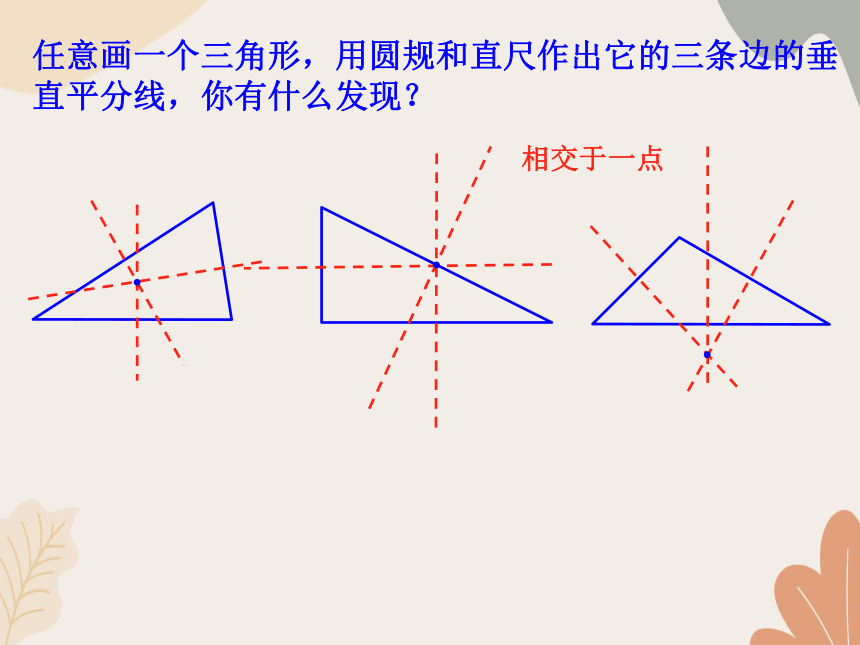
任意画一个三角形,用圆规和直尺作出它的三条边的垂直平分线,你有什么发现?
相交于一点
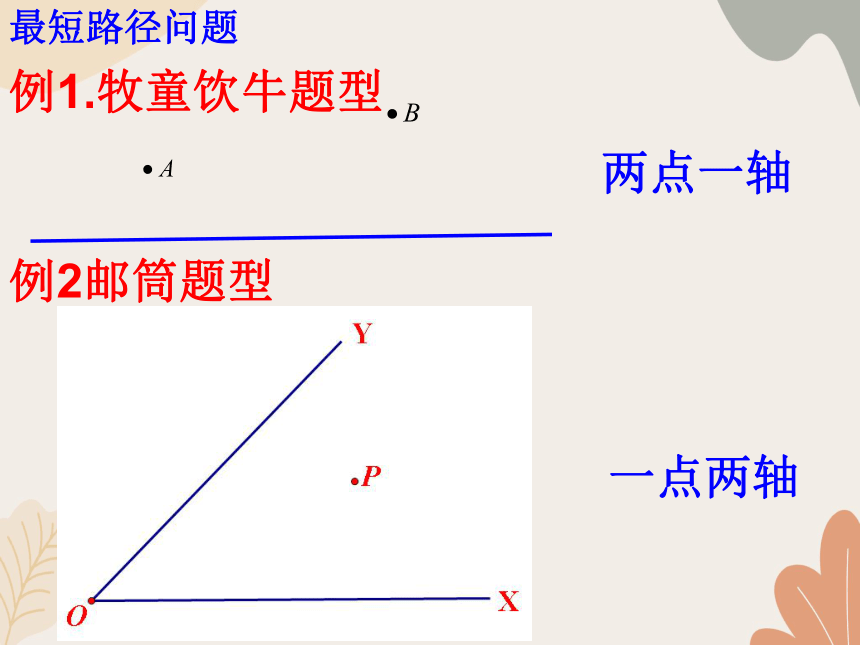
例1.牧童饮牛题型
例2邮筒题型
一点两轴
最短路径问题
两点一轴
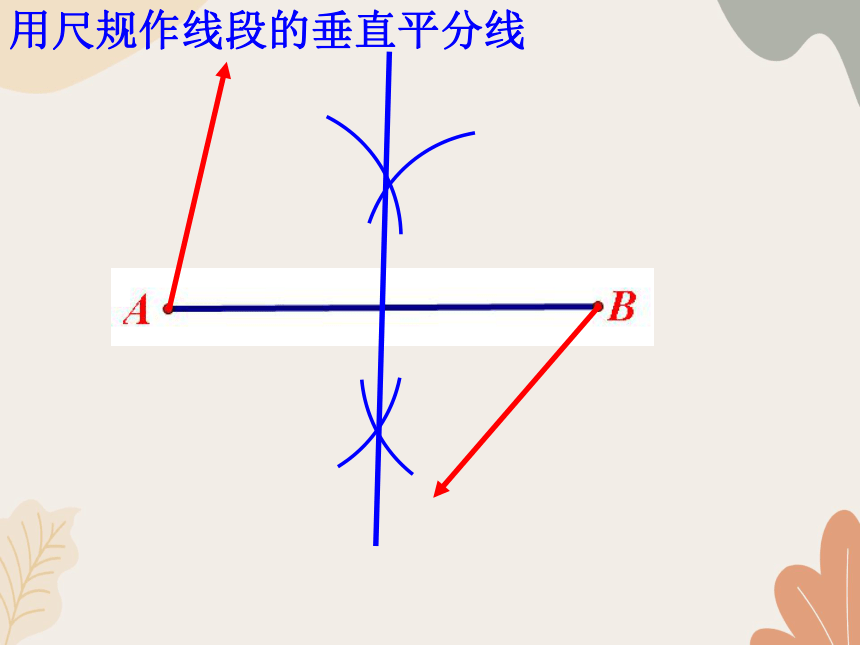
用尺规作线段的垂直平分线
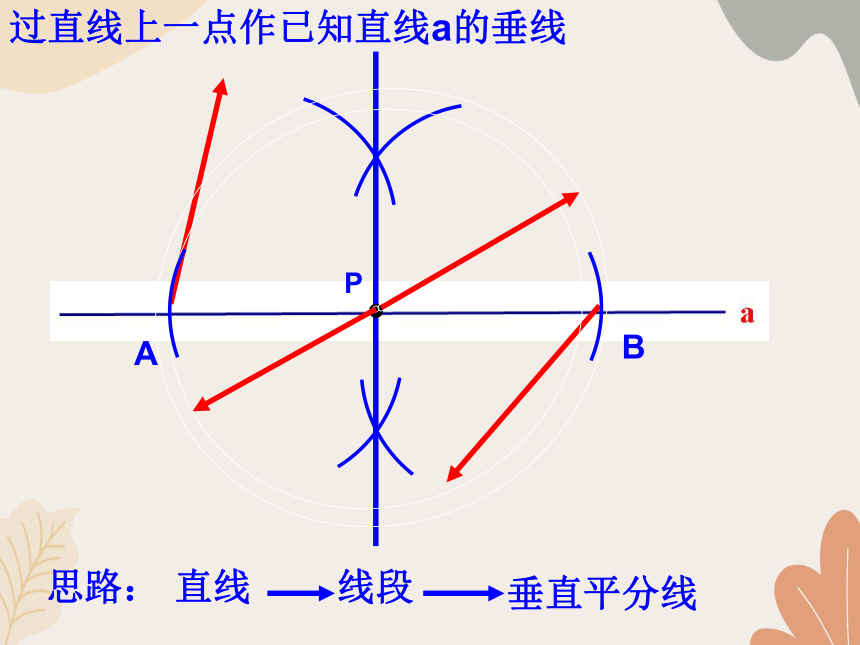
过直线上一点作已知直线a的垂线
A
B
P
思路:
直线
线段
垂直平分线
例2:过直线外一点作已知直线a的垂线
A
B
P
K
思路:
直线
线段
垂直平分线
P
M
N
角平分线的性质:
角的平分线上的点到这个角的两边的距离相等。
数学语言:
∵AD是∠BAC的角平分线,
PM⊥AB,PN⊥AC(已知)
∴PM=PN
已知:如图,△ABC的角平分线BM、CN相交于点P。
求证:点P到三边AB、BC、CA的距离相等。
证明:过点P作PD、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,
PD⊥AB,PE⊥BC(已知)
∴PD=PE(角平分线上的点到这个角两边的距离相等)
同理PE=PF.
∴PD=PE=PF.
即点P到边AB、BC、CA的距离相等
D
E
F
A
B
C
P
M
N
内心的性质是什么?
到三角形三条边的距离相等。
举手回答
内心是什么的交点?
举手回答
三角形三个内角的角平分线的交点。
角的内部到角的两边距离相等的点在角的平分线上。
一、角平分线的性质的逆用
P
C
D
E
∵PD=PE,PD⊥OA,PE⊥OB
∴点P在∠AOB的平分线上。
数学语言:
例1:三角形三内角平分线交于一点
P
已知:∠A和∠B的角平分线交于点P
D
E
F
求证:点P在∠C的平分线上。
过点P作PD、PE、PF分别垂直于BC、AC、AB,
垂足为D、E、F
证明:
∵BP是∠ABC的角平分线,
PD⊥BC,PF⊥AB(已知)
∴PD=PF
(角平分线上的点到这个角两边的距离相等)
同理PE=PF.
∴PD=PE
PD⊥BC,PE⊥AC(已知)
∴点P在∠C的平分线上
综上:三角形三个内角平分线交于一点。
(角的内部到角的两边距离相等的点在角的平分线上)
D
4
如图,A、B、C三村欲合修一加油站,使它到道路AB、BC、AC的距离相等,如何找到这个位置?共有几处?
尺规作角的平分线
观察领悟作法,探索思考证明方法:
A
B
O
M
N
C
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OBN于。
2.分别以M,N为圆心.大于1/2MN的长为半径作弧.两弧在∠AOB的内部交于C。
3.作射线OC。
射线OC即为所求。
A
B
M
N
C
为什么OC是角平分线呢?
O
O
想一想:
已知:OM=ON,MC=NC。
求证:OC平分∠AOB。
证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴△OMC≌△ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
A
B
M
N
C
O
O
O
A
B
.C
.D
在V型公路(∠AOB)内部,有两个村庄C、D。你能选择一个纺织厂的厂址P,使P到V型公路的距离相等,且使C、D两村的工人上下班的路程一样吗?
等腰三角形的性质
3、等腰三角形的两个底角相等
(简称“等边对等角”)
2、等腰三角形的底边上的高、底边上的中线及顶角平分线重合。
A
B
C
D
1、等腰三角形是轴对称图形。等腰三角形的对称轴是底边的垂直平分线
(1)∵AB=AC,AD⊥BC,
∴∠____=∠____,___=___
(2)∵AB=AC,AD是中线,
∴___⊥___,∠____=∠____
(3)∵AB=AC,AD是角平分线,
∴___⊥___,___=___
BAD CAD
BD CD
AD BC
AD BC
BAD CAD
BD CD
等腰三角形三线合一性质应用的几何语言,如图所示,在△ABC中
A
D
C
B
C
A
B
等腰三角形的判定定理:
1.有两边相等的三角形是等腰三角形
2.有两个角相等的三角形是等腰三角形
(简写成“等角对等边”)
数学语言:
∵AB=AC(已知)
∴△ABC是等腰三角形
∵∠B=∠C(已知)
∴AB=AC(等角对等边)
∴△ABC是等腰三角形
1、等腰三角形一个底角为70°,它的顶角为______。
小试牛刀
2、等腰三角形一个角为70°,它的另外两个角为
_______________________。
3、等腰三角形一个角为110°,它的另外两个角为___________。
①顶角度数+2×底角度数=180°
②0°<顶角度数<180°
③0°<底角度数<90°
结论:在等腰三角形中,
40°
35°,35°
70°,40°或55°,55°
1、等腰三角形一腰上的高与另一腰的夹角为 ,
则顶角的度数为多少度?
腰高题型
2、已知一个等腰三角形腰上的高与另一腰的夹角为45°,顶角的度数为多少度?
等腰三角形中一腰上的中线把三角形的周长分为21cm和12cm两部分,则腰长为多少?
如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
6
钢筋架题型
……
8
③
已知等边三角形ABC和点P,设点P到△ABC三边AB,AC,BC的距离分别是h1,h2,h3,△ABC的高为h,请你探索以下问题:
(1)若点P在一边BC上(如图①),此时h3=0,
问h1,h2与h之间有怎样的关系?请说明理由。
(2)若点P在△ABC内部(如图②),
此时h1,h2,h3与h之间有怎样的关系?请说明理由。
(3)若点P在△ABC外部(如图③),
此是h1,h2,h3与h之间有怎样的关系?请说明理由。
①
②
等边三角形的性质
2.等边三角形的内角都相等,且等于60°
3.等边三角形各边上中线,高和所对角的平分线都三线合一。
4.等边三角形是轴对称图形,有三条对称轴。
1.三条边相等
等边三角形三种判定方法
三边都相等的三角形是等边三角形。
三个角都相等的三角形是等边三角形。
∵AB=BC=AC
∴△ABC是等边三角形
∵∠A=∠B=∠C
∴△ABC是等边三角形
∵∠A=600,AB=BC
∴△ABC是等边三角形
有一个角是60°的等腰三角形是等边三角形。
课堂小结
1、如果一个图形沿某一条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴,对折后图形上能够重合的点叫对称点。
2、如果把一个图形沿某一条直线折叠后,能够与另一个图形完全重合,那么这两个图形关于这条直线成轴对称。这条直线叫做它们的对称轴。折叠后两个图形上互相重合的点叫对称点。
你能说说它们的区别与联系吗?
区别:轴对称图形是指一个具有特殊形状的图形;两个图形关于某一条直线成轴对称是指两个图形的特殊形状和位置关系。
联系:①都有一条直线,都沿直线折叠重合;②若把轴对称图形沿对称轴分成两部分,则这两个图形关于这条直线成轴对称;若把两个关于某直线成轴对称的图形看作一个整体,则它就是一个轴对称图形。
l
75°
2.29
3.20
3.44
43°
A
B
C
D
E
F
图中两个三角形关于直线l成轴对称。
如果三角形的部分边长(单位:厘米)
和角的度数如图所示,求未知的边长
和角的度数。
l
75°
2.29
3.20
3.44
43°
A
B
C
D
E
F
AC=DF=3.20
BC=EF=3.44
AB=DE=2.29
∴
∴∠D=∠A=75°,∠C=∠F=43°
已知对称轴l和一个
点A如何画出点A关于
l的对称点A′?
3、点A′就是点A关于l的对称点.
A
A′
1、过点A作对称轴l的垂线,垂足为B;
2、延长AB至A′ ,使得BA′ =AB.
B
l
例1:
如何画线段AB关于直线 的
对称线段A′ B′ ?
找关键点作出其对称点!然后连结线段.
A
B
A′
B′
例2:
思路:
如何画△ABC关于直线 的对称△A′B′C′?
还是找关键点作出其对称点!
然后顺次连结线段构成三角形。
例3:
B′
A′
A
B
思路:
C′
C
谢 谢
第2的轴对称
复习课件
图形的轴对称
轴对称:
线段
角
等腰三角形
对称轴
线段的垂直平分线
性质
③尺规作图
性质
画图
各种题型
等边三角形
性质
判定
轴对称图形
判定
对称轴
角平分线所在的直线
性质
③尺规作图
判定
性质
判定
坐标轴坐标的规律。
一.线段垂直平分线的性质
线段垂直平分线上的点到线段两端的距离相等。
M
N
P
C
几何语言1:
∵PC⊥AB,AC=BC(已知)
∴PA=PB(线段垂直平分线上的点到线段两端的距离相等。)
几何语言2:
∵MN垂直平分AB(已知)
∴PA=PB(线段垂直平分线上的点到线段两端点的距离相等。)
例1已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P。
求证:PA=PB=PC
证明:
∵MN垂直平分AB
∴PA=PB
同理PB=PC
∴PA=PB=PC
B
A
C
M
N
M′
N′
P
B
A
C
M
N
M′
N′
P
外心的性质是什么?
到三角形三个顶点的距离相等。
举手回答
B
A
C
M
N
M′
N′
P
外心是什么的交点?
三角形三条边垂直平分线的交点。
举手回答
到线段两端距离相等的点在线段的垂直平分线上。
P
∵PA=PB
∴点P在线段AB的垂直平分线上
二.线段垂直平分线的判定
数学语言:
任意画一个三角形,用圆规和直尺作出它的三条边的垂直平分线,你有什么发现?
相交于一点
例1.牧童饮牛题型
例2邮筒题型
一点两轴
最短路径问题
两点一轴
用尺规作线段的垂直平分线
过直线上一点作已知直线a的垂线
A
B
P
思路:
直线
线段
垂直平分线
例2:过直线外一点作已知直线a的垂线
A
B
P
K
思路:
直线
线段
垂直平分线
P
M
N
角平分线的性质:
角的平分线上的点到这个角的两边的距离相等。
数学语言:
∵AD是∠BAC的角平分线,
PM⊥AB,PN⊥AC(已知)
∴PM=PN
已知:如图,△ABC的角平分线BM、CN相交于点P。
求证:点P到三边AB、BC、CA的距离相等。
证明:过点P作PD、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,
PD⊥AB,PE⊥BC(已知)
∴PD=PE(角平分线上的点到这个角两边的距离相等)
同理PE=PF.
∴PD=PE=PF.
即点P到边AB、BC、CA的距离相等
D
E
F
A
B
C
P
M
N
内心的性质是什么?
到三角形三条边的距离相等。
举手回答
内心是什么的交点?
举手回答
三角形三个内角的角平分线的交点。
角的内部到角的两边距离相等的点在角的平分线上。
一、角平分线的性质的逆用
P
C
D
E
∵PD=PE,PD⊥OA,PE⊥OB
∴点P在∠AOB的平分线上。
数学语言:
例1:三角形三内角平分线交于一点
P
已知:∠A和∠B的角平分线交于点P
D
E
F
求证:点P在∠C的平分线上。
过点P作PD、PE、PF分别垂直于BC、AC、AB,
垂足为D、E、F
证明:
∵BP是∠ABC的角平分线,
PD⊥BC,PF⊥AB(已知)
∴PD=PF
(角平分线上的点到这个角两边的距离相等)
同理PE=PF.
∴PD=PE
PD⊥BC,PE⊥AC(已知)
∴点P在∠C的平分线上
综上:三角形三个内角平分线交于一点。
(角的内部到角的两边距离相等的点在角的平分线上)
D
4
如图,A、B、C三村欲合修一加油站,使它到道路AB、BC、AC的距离相等,如何找到这个位置?共有几处?
尺规作角的平分线
观察领悟作法,探索思考证明方法:
A
B
O
M
N
C
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OBN于。
2.分别以M,N为圆心.大于1/2MN的长为半径作弧.两弧在∠AOB的内部交于C。
3.作射线OC。
射线OC即为所求。
A
B
M
N
C
为什么OC是角平分线呢?
O
O
想一想:
已知:OM=ON,MC=NC。
求证:OC平分∠AOB。
证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴△OMC≌△ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
A
B
M
N
C
O
O
O
A
B
.C
.D
在V型公路(∠AOB)内部,有两个村庄C、D。你能选择一个纺织厂的厂址P,使P到V型公路的距离相等,且使C、D两村的工人上下班的路程一样吗?
等腰三角形的性质
3、等腰三角形的两个底角相等
(简称“等边对等角”)
2、等腰三角形的底边上的高、底边上的中线及顶角平分线重合。
A
B
C
D
1、等腰三角形是轴对称图形。等腰三角形的对称轴是底边的垂直平分线
(1)∵AB=AC,AD⊥BC,
∴∠____=∠____,___=___
(2)∵AB=AC,AD是中线,
∴___⊥___,∠____=∠____
(3)∵AB=AC,AD是角平分线,
∴___⊥___,___=___
BAD CAD
BD CD
AD BC
AD BC
BAD CAD
BD CD
等腰三角形三线合一性质应用的几何语言,如图所示,在△ABC中
A
D
C
B
C
A
B
等腰三角形的判定定理:
1.有两边相等的三角形是等腰三角形
2.有两个角相等的三角形是等腰三角形
(简写成“等角对等边”)
数学语言:
∵AB=AC(已知)
∴△ABC是等腰三角形
∵∠B=∠C(已知)
∴AB=AC(等角对等边)
∴△ABC是等腰三角形
1、等腰三角形一个底角为70°,它的顶角为______。
小试牛刀
2、等腰三角形一个角为70°,它的另外两个角为
_______________________。
3、等腰三角形一个角为110°,它的另外两个角为___________。
①顶角度数+2×底角度数=180°
②0°<顶角度数<180°
③0°<底角度数<90°
结论:在等腰三角形中,
40°
35°,35°
70°,40°或55°,55°
1、等腰三角形一腰上的高与另一腰的夹角为 ,
则顶角的度数为多少度?
腰高题型
2、已知一个等腰三角形腰上的高与另一腰的夹角为45°,顶角的度数为多少度?
等腰三角形中一腰上的中线把三角形的周长分为21cm和12cm两部分,则腰长为多少?
如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
6
钢筋架题型
……
8
③
已知等边三角形ABC和点P,设点P到△ABC三边AB,AC,BC的距离分别是h1,h2,h3,△ABC的高为h,请你探索以下问题:
(1)若点P在一边BC上(如图①),此时h3=0,
问h1,h2与h之间有怎样的关系?请说明理由。
(2)若点P在△ABC内部(如图②),
此时h1,h2,h3与h之间有怎样的关系?请说明理由。
(3)若点P在△ABC外部(如图③),
此是h1,h2,h3与h之间有怎样的关系?请说明理由。
①
②
等边三角形的性质
2.等边三角形的内角都相等,且等于60°
3.等边三角形各边上中线,高和所对角的平分线都三线合一。
4.等边三角形是轴对称图形,有三条对称轴。
1.三条边相等
等边三角形三种判定方法
三边都相等的三角形是等边三角形。
三个角都相等的三角形是等边三角形。
∵AB=BC=AC
∴△ABC是等边三角形
∵∠A=∠B=∠C
∴△ABC是等边三角形
∵∠A=600,AB=BC
∴△ABC是等边三角形
有一个角是60°的等腰三角形是等边三角形。
课堂小结
1、如果一个图形沿某一条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴,对折后图形上能够重合的点叫对称点。
2、如果把一个图形沿某一条直线折叠后,能够与另一个图形完全重合,那么这两个图形关于这条直线成轴对称。这条直线叫做它们的对称轴。折叠后两个图形上互相重合的点叫对称点。
你能说说它们的区别与联系吗?
区别:轴对称图形是指一个具有特殊形状的图形;两个图形关于某一条直线成轴对称是指两个图形的特殊形状和位置关系。
联系:①都有一条直线,都沿直线折叠重合;②若把轴对称图形沿对称轴分成两部分,则这两个图形关于这条直线成轴对称;若把两个关于某直线成轴对称的图形看作一个整体,则它就是一个轴对称图形。
l
75°
2.29
3.20
3.44
43°
A
B
C
D
E
F
图中两个三角形关于直线l成轴对称。
如果三角形的部分边长(单位:厘米)
和角的度数如图所示,求未知的边长
和角的度数。
l
75°
2.29
3.20
3.44
43°
A
B
C
D
E
F
AC=DF=3.20
BC=EF=3.44
AB=DE=2.29
∴
∴∠D=∠A=75°,∠C=∠F=43°
已知对称轴l和一个
点A如何画出点A关于
l的对称点A′?
3、点A′就是点A关于l的对称点.
A
A′
1、过点A作对称轴l的垂线,垂足为B;
2、延长AB至A′ ,使得BA′ =AB.
B
l
例1:
如何画线段AB关于直线 的
对称线段A′ B′ ?
找关键点作出其对称点!然后连结线段.
A
B
A′
B′
例2:
思路:
如何画△ABC关于直线 的对称△A′B′C′?
还是找关键点作出其对称点!
然后顺次连结线段构成三角形。
例3:
B′
A′
A
B
思路:
C′
C
谢 谢
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
