人教版八年级数学上名师点拨精练第12章全等三角形12.2 三角形全等的判定2
文档属性
| 名称 | 人教版八年级数学上名师点拨精练第12章全等三角形12.2 三角形全等的判定2 |  | |
| 格式 | doc | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-07 20:56:42 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.2 三角形全等的判定2
学习目标
1.能够利用尺规正确的画出一个与给定三角形满足SAS条件的全等的三角形,能准确叙述SAS.
2.能够利用SAS进行简单的几何推理(计算或证明)
3.能够利用SAS进行较复杂的几何推理(计算或证明)
4.能画图说明满足SSA条件的两个三角形不一定全等.能够综合利用SSS、SAS进行复杂的几何推理.
老师告诉你
倍长中线法:
遇到三角形的中线(中点)问题时,常将中线延长一倍(这种方法称倍长中线法),然后连接相应的顶点,构造全等三角形,通过全等三角形的性质将线段的关系进行转化,从而达到解决问题的目的。
知识点拨
知识点1 全等三角形的判定2:边角边(SAS)
三角形全等的判定2:边角边(SAS)
文字:在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等;
图形:
符号:在与中,.
【新知导学】
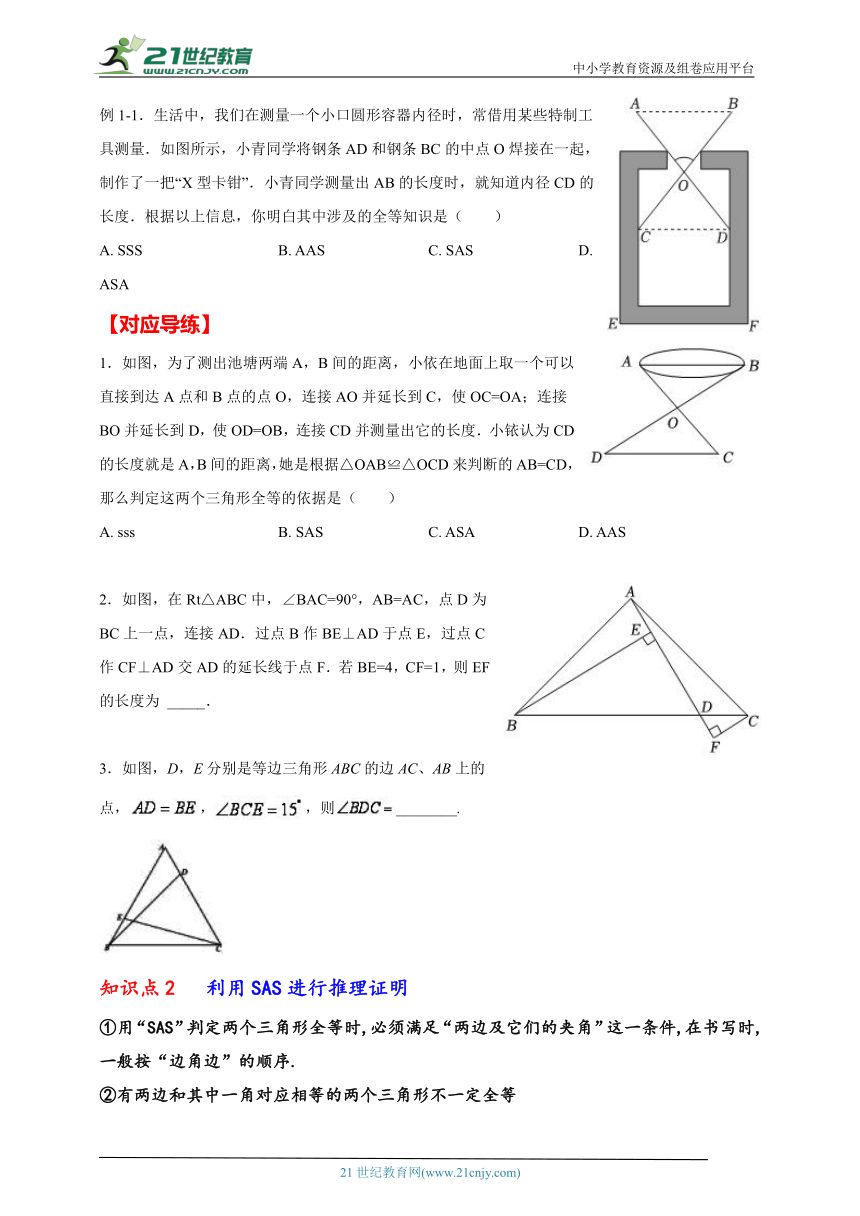
例1-1.生活中,我们在测量一个小口圆形容器内径时,常借用某些特制工具测量.如图所示,小青同学将钢条AD和钢条BC的中点O焊接在一起,制作了一把“X型卡钳”.小青同学测量出AB的长度时,就知道内径CD的长度.根据以上信息,你明白其中涉及的全等知识是( )
A. SSS B. AAS C. SAS D. ASA
【对应导练】
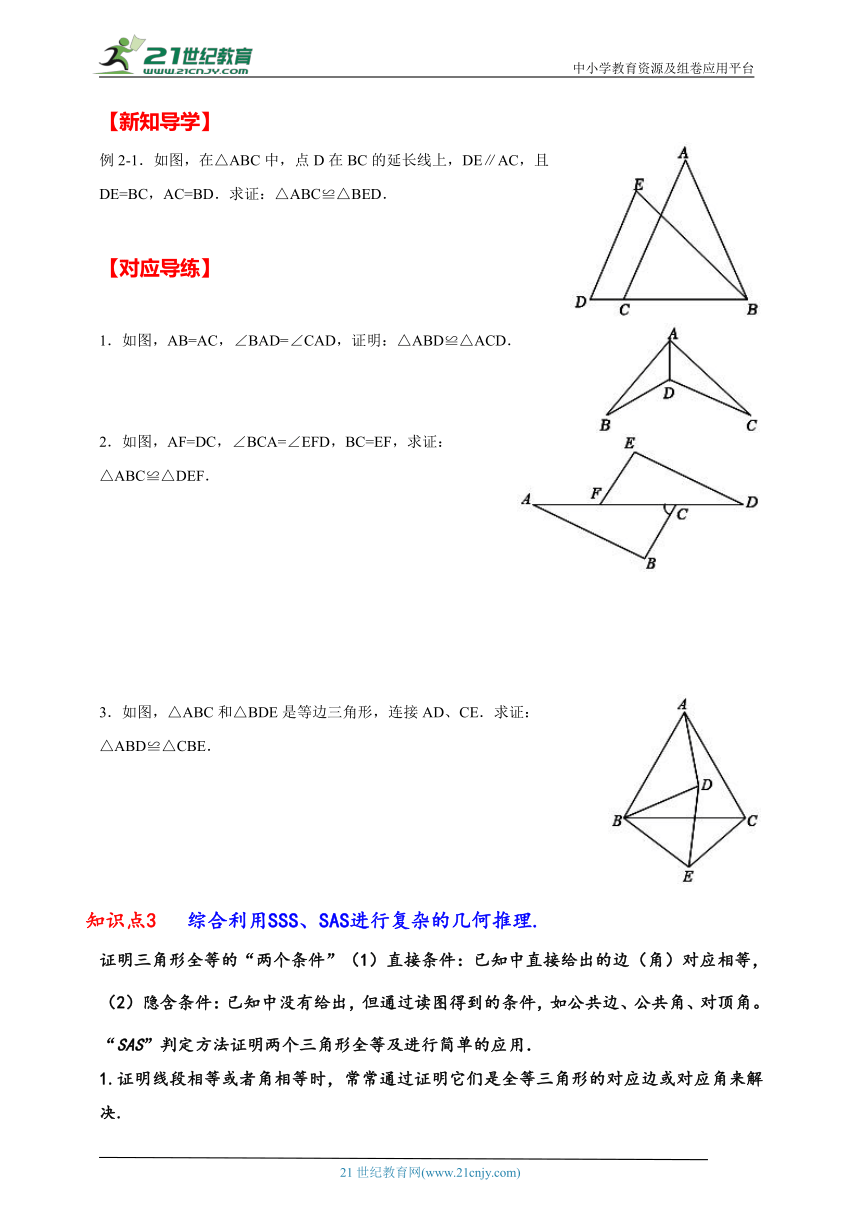
1.如图,为了测出池塘两端A,B间的距离,小依在地面上取一个可以直接到达A点和B点的点O,连接AO并延长到C,使OC=OA;连接BO并延长到D,使OD=OB,连接CD并测量出它的长度.小铱认为CD的长度就是A,B间的距离,她是根据△OAB≌△OCD来判断的AB=CD,那么判定这两个三角形全等的依据是( )
A. sss B. SAS C. ASA D. AAS
2.如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC上一点,连接AD.过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F.若BE=4,CF=1,则EF的长度为 _____.
3.如图,D,E分别是等边三角形ABC的边AC、AB上的点,,,则________.
知识点2 利用SAS进行推理证明
①用“SAS”判定两个三角形全等时,必须满足“两边及它们的夹角”这一条件,在书写时,一般按“边角边”的顺序.
②有两边和其中一角对应相等的两个三角形不一定全等
【新知导学】
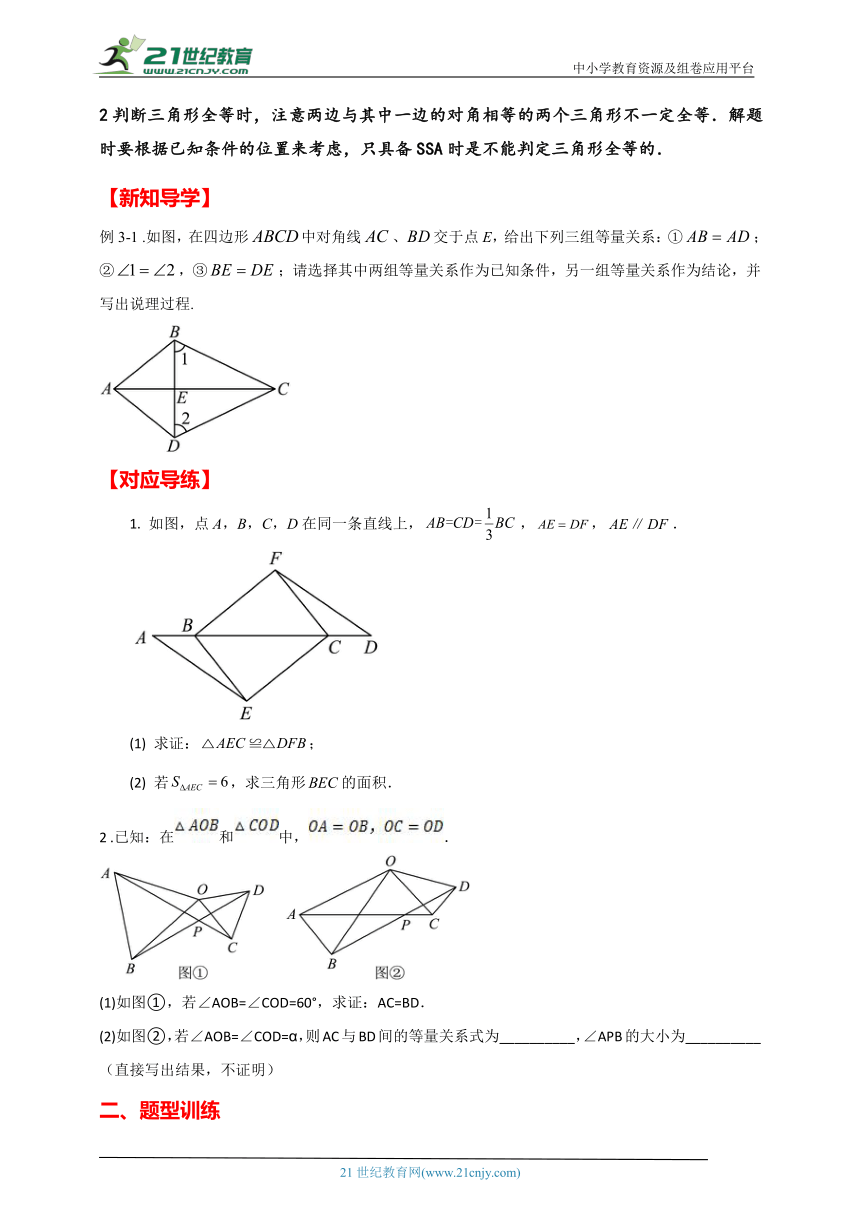
例2-1.如图,在△ABC中,点D在BC的延长线上,DE∥AC,且DE=BC,AC=BD.求证:△ABC≌△BED.
【对应导练】
1.如图,AB=AC,∠BAD=∠CAD,证明:△ABD≌△ACD.
2.如图,AF=DC,∠BCA=∠EFD,BC=EF,求证:△ABC≌△DEF.
3.如图,△ABC和△BDE是等边三角形,连接AD、CE.求证:△ABD≌△CBE.
知识点3 综合利用SSS、SAS进行复杂的几何推理.
证明三角形全等的“两个条件”(1)直接条件:已知中直接给出的边(角)对应相等,
隐含条件:已知中没有给出,但通过读图得到的条件,如公共边、公共角、对顶角。
“SAS”判定方法证明两个三角形全等及进行简单的应用.
1.证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.
2判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
【新知导学】
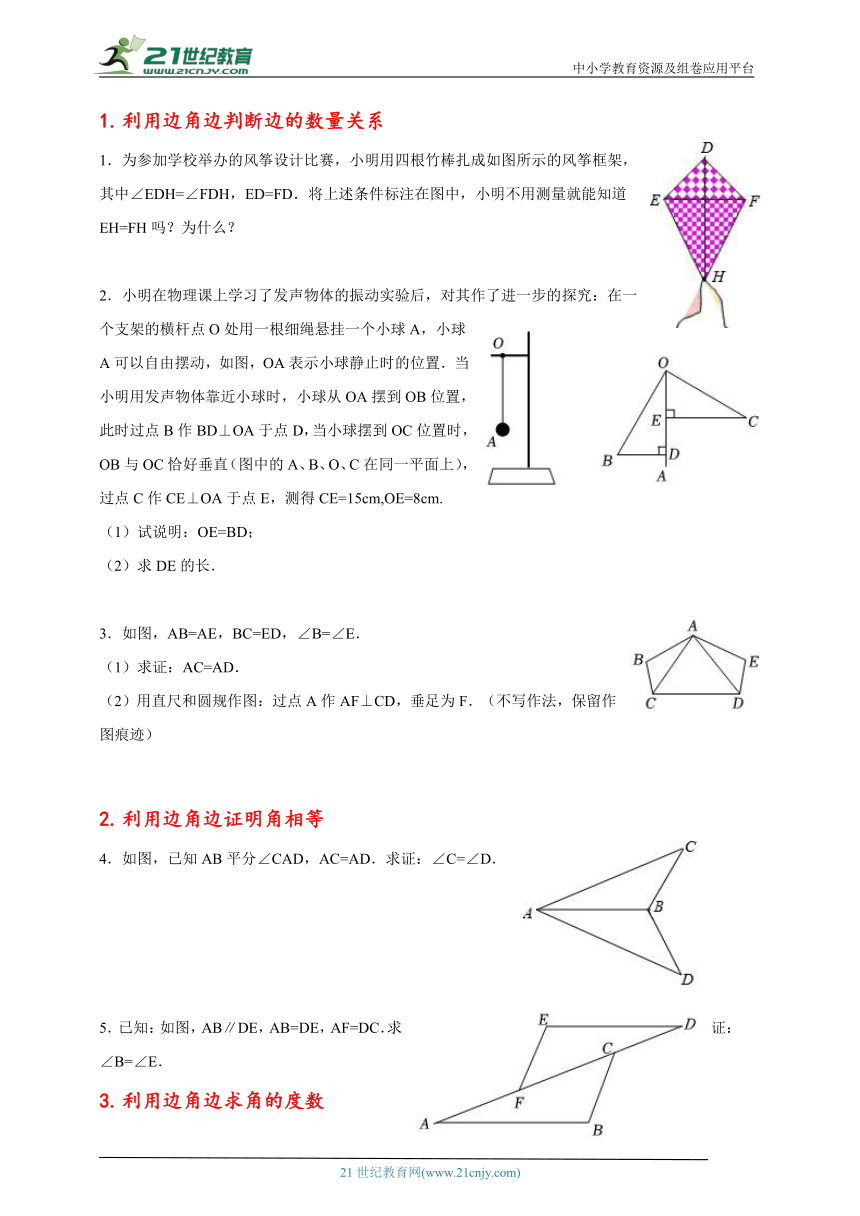
例3-1 .如图,在四边形中对角线、交于点E,给出下列三组等量关系:①;②,③;请选择其中两组等量关系作为已知条件,另一组等量关系作为结论,并写出说理过程.
【对应导练】
如图,点A,B,C,D在同一条直线上,,,.
求证:;
若,求三角形的面积.
2 .已知:在和中,.
(1)如图①,若∠AOB=∠COD=60°,求证:AC=BD.
(2)如图②,若∠AOB=∠COD=α,则AC与BD间的等量关系式为__________,∠APB的大小为__________(直接写出结果,不证明)
题型训练
利用边角边判断边的数量关系
1.为参加学校举办的风筝设计比赛,小明用四根竹棒扎成如图所示的风筝框架,其中∠EDH=∠FDH,ED=FD.将上述条件标注在图中,小明不用测量就能知道EH=FH吗?为什么?
2.小明在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆点O处用一根细绳悬挂一个小球A,小球A可以自由摆动,如图,OA表示小球静止时的位置.当小明用发声物体靠近小球时,小球从OA摆到OB位置,此时过点B作BD⊥OA于点D,当小球摆到OC位置时,OB与OC恰好垂直(图中的A、B、O、C在同一平面上),过点C作CE⊥OA于点E,测得CE=15cm,OE=8cm.
(1)试说明:OE=BD;
(2)求DE的长.
3.如图,AB=AE,BC=ED,∠B=∠E.
(1)求证:AC=AD.
(2)用直尺和圆规作图:过点A作AF⊥CD,垂足为F.(不写作法,保留作图痕迹)
利用边角边证明角相等
4.如图,已知AB平分∠CAD,AC=AD.求证:∠C=∠D.
5.已知:如图,AB∥DE,AB=DE,AF=DC.求证:∠B=∠E.
利用边角边求角的度数
6.如图,点,分别是边长为的等边的边,上的动点,点从点向点运动,点从点向点运动,它们同时出发,且速度都为,运动的时间为秒,连接,交于点,则在,运动的过程中,
(1)求证:;
(2)的大小变化吗?若变化,则说明理由,若不变,则求出它的度数;
7.如图,在 ABC中,BE,CF分别是AC,AB边上的高,在BE上取一点D,使DB=AC,在射线CF上取一点G,使GC=AB,连结AG,AD.若∠DAE=38°,∠ABE,则∠G的度数为 .
综合边边边、边角边进行计算证明
8.已知四边形中,,,如图2,点P,Q分别在线段,上,满足,求证:.
牛刀小试
一、单选题(每小题4分,共32分)
1.如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
2.如图,已知,添加一个条件,使得,下列条件添加错误的是( )
A. B. C. D.
3.如图,在与中,,,,,AB交EF于点D,连接EB.下列结论:
①;
②;
③;
④,正确的个数为( )
A.4个 B.3个 C.2个 D.1个
4.我国的纸伞工艺十分巧妙,如图,伞圈D能沿着伞柄滑动,伞不论张开还是缩拢,伞柄始终平分同一平面内所成的角,为了证明这个结论,我们的依据是( )
A. B. C. D.
5.如图,在和中,,,要使,则可以添加下列哪个条件( )
A. B. C. D.
6.根据下列图中所给定的条件,找出全等的三角形( )
A.①和② B.②和③ C.①和③ D.①和④
7.如图,,要使,还需添加一个条件是( )
A. B. C. D.
如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点均在小正方形方格的顶点上,线段交于点,若,则等于( )
A. B. C. D.
二、填空题(每小题4分,共20分)
9.如图,A,B两点分别位于一个池塘的两端,小凡想用绳子测量A,B间的距离,但无法从A点直接到达B点,聪明的小凡想出一个办法:先在地上选取一个可以直接到达B点的点C,连接BC,取BC的中点P(点P可以直接到达A点),连接AP并延长到点D,使DP=AP.连接CD,并测量出它的长度为10米,则A,B两点间的距离为 _____米.
10.“三月三,放风筝”,如图是小明制作的风筝,他根据DE=DF,EH=FH,不用测量,就知道∠DEH=∠DFH,小明是通过全等三角形的知识得到的结论,则小明判定三角形全等的依据是_____(用字母表示).
11.如图所示.A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1km,DC=1km,村庄AC,AD间也有公路相连,且公路AD是南北走向,AC=3km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2km,BF=0.7km.试求建造的斜拉桥长至少有___________km.
12.如图,一块三角形玻璃裂成①②两块,现需配一块同样的玻璃,为方便起见,只需带上碎片_____即可.
13.如图,在△ABC中,AB=AC,D为BC上的一点,∠BAD=28°,在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE,DE,DE交AC于点O,若CE∥AB,则∠DOC的度数为 _____.
三、解答题(共6小题,共48分)
14.(8分)(1)萧县某中学计划为学生暑期军训配备如图(1)所示的折叠凳,这样设计的折叠凳坐着舒适、稳定.这种设计所运用的数学原理是 _____;
(2)图(2)是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,交点O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为38cm,则由以上信息可推得CB的长度是多少?请说明理由.
15.(8分)如图,AB=AC,D为△ABC内部一点,且BD=CD.连接AD并延长,交BC于点E.
①请写出图中两组全等的三角形;
②任选其一说明全等的理由.
16.(8分)已知如图,在四边形ABCD中,AB=CD,AD=BC,求证:∠A=∠C.
17.(8分)如图,等腰梯形ABCD中,AD∥BC,P为等腰梯形内部一点,若PA=PD,试说明PB=PC.
18 .(8分)如图,在 ABC中,∠B=50°,∠C=20°.过点A作AE⊥BC,垂足为E,延长EA至点D.使AD=AC.在边AC上截取AF=AB,连接DF.求证:DF=CB.
19 .(10分)问题发现:如图1,已知C为线段AB上一点,分别以线段AC,BC为直角边作等腰直角三角形,∠ACD=90°,CA=CD,CB=CE,连接AE,BD,线段AE,BD之间的数量关系为______;位置关系为_______.
拓展探究:如图2,把Rt ACD绕点C逆时针旋转,线段AE,BD交于点F,则AE与BD之间的关系是否仍然成立?请说明理由.
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.2 三角形全等的判定2
学习目标
1.能够利用尺规正确的画出一个与给定三角形满足SAS条件的全等的三角形,能准确叙述SAS.
2.能够利用SAS进行简单的几何推理(计算或证明)
3.能够利用SAS进行较复杂的几何推理(计算或证明)
4.能画图说明满足SSA条件的两个三角形不一定全等.能够综合利用SSS、SAS进行复杂的几何推理.
老师告诉你
倍长中线法:
遇到三角形的中线(中点)问题时,常将中线延长一倍(这种方法称倍长中线法),然后连接相应的顶点,构造全等三角形,通过全等三角形的性质将线段的关系进行转化,从而达到解决问题的目的。
知识点拨
知识点1 全等三角形的判定2:边角边(SAS)
三角形全等的判定2:边角边(SAS)
文字:在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等;
图形:
符号:在与中,.
【新知导学】
例1-1.生活中,我们在测量一个小口圆形容器内径时,常借用某些特制工具测量.如图所示,小青同学将钢条AD和钢条BC的中点O焊接在一起,制作了一把“X型卡钳”.小青同学测量出AB的长度时,就知道内径CD的长度.根据以上信息,你明白其中涉及的全等知识是( )
A. SSS B. AAS C. SAS D. ASA
【答案】C
【解析】根据全等三角形的判定定理即可得到结论.
解:在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
故选:C.
【对应导练】
1.如图,为了测出池塘两端A,B间的距离,小依在地面上取一个可以直接到达A点和B点的点O,连接AO并延长到C,使OC=OA;连接BO并延长到D,使OD=OB,连接CD并测量出它的长度.小铱认为CD的长度就是A,B间的距离,她是根据△OAB≌△OCD来判断的AB=CD,那么判定这两个三角形全等的依据是( )
A. sss B. SAS C. ASA D. AAS
【答案】B
【解析】由题意知OA=OC,OB=OD,由于∠AOB=∠COD,根据“SAS”即可证明△OAB≌△OCD.
解:由题意知OA=OC,OB=OD,
在△OAB和△OCD中,
,
∴△OAB≌△OCD(SAS).
故选:B.
2.如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC上一点,连接AD.过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F.若BE=4,CF=1,则EF的长度为 _____.
【答案】3
【解析】先证明△ABE≌△CAF(AAS),根据全等三角形的性质可得AF=BE=4,AE=CF=1,进一步可得EF的长.
解:∵BE⊥AD,CF⊥AD,
∴∠BEA=∠AFC=90°,
∴∠BAE+∠ABE=90°,
∵∠BAC=90°,
∴∠BAE+∠FAC=90°,
∴∠FAC=∠ABE,
在△ABE和△CAF中,
,
∴△ABE≌△CAF(AAS),
∴AF=BE,AE=CF,
∵BE=4,CF=1,
∴AF=BE=4,AE=CF=1,
∴EF=AF-AE=4-1=3,
故答案为:3.
3.如图,D,E分别是等边三角形ABC的边AC、AB上的点,,,则________.
【答案】
【解析】可证 可得∠ABD=∠BCE=15°由三角形外角即可计算∠BDC的度数.
解:在等边三角形ABC中:AB=BC,∠BAD=∠CBE=60°
∵
∴
∴∠ABD=∠BCE=15°
∴∠BDC=∠ABD+∠A=15°+60°=75°
故答案为75°
【点睛】本题考查了全等三角形的判定及应用,掌握三角形的判定是解题的关键.
知识点2 利用SAS进行推理证明
①用“SAS”判定两个三角形全等时,必须满足“两边及它们的夹角”这一条件,在书写时,一般按“边角边”的顺序.
②有两边和其中一角对应相等的两个三角形不一定全等
【新知导学】
例2-1.如图,在△ABC中,点D在BC的延长线上,DE∥AC,且DE=BC,AC=BD.求证:△ABC≌△BED.
【解析】根据平行线的性质得出∠D=∠ACB,再根据全等三角形的判定定理SAS推出即可.
证明:∵DE∥AC,
∴∠D=∠ACB,
在△ABC和△BED中,
,
∴△ABC≌△BED(SAS).
【对应导练】
1.如图,AB=AC,∠BAD=∠CAD,证明:△ABD≌△ACD.
【解析】根据“SAS”可判断△ABD≌△ACD.
证明:在△ABD和△ACD 中,
,
∴△ABD≌△ACD(SAS).
2.如图,AF=DC,∠BCA=∠EFD,BC=EF,求证:△ABC≌△DEF.
【解析】求出AC=DF,再根据全等三角形的判定定理SAS推出即可.
证明:∵AF=DC,
∴AF+FC=DC+CF,
即AC=DF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
3.如图,△ABC和△BDE是等边三角形,连接AD、CE.求证:△ABD≌△CBE.
【解析】根据等边三角形的性质得出AB=BC,BD=BE,进而利用SAS证明△ABD≌△CBE即可.
证明:∵△ABC,△BDE是等边三角形,
∴∠ABC=∠DBE=60°,AB=BC,BD=BE,
∴∠ABC-∠DBC=∠DBE-∠DBC,
∴∠ABD=∠CBE,
在△ABD和△CBE中,
,
∴△ABD≌△CBE(SAS).
知识点3 综合利用SSS、SAS进行复杂的几何推理.
证明三角形全等的“两个条件”(1)直接条件:已知中直接给出的边(角)对应相等,
隐含条件:已知中没有给出,但通过读图得到的条件,如公共边、公共角、对顶角。
“SAS”判定方法证明两个三角形全等及进行简单的应用.
1.证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.
2判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
【新知导学】
例3-1 .如图,在四边形中对角线、交于点E,给出下列三组等量关系:①;②,③;请选择其中两组等量关系作为已知条件,另一组等量关系作为结论,并写出说理过程.
答案:选择①③,证明②,证明见解析
解析:选择①③,证明②,
证明:在与中,
,
,
,
在与中,
,
,
,
.
【对应导练】
1.如图,点A,B,C,D在同一条直线上,,,.
求证:;
若,求三角形的面积.
【答案】(1) 见分析; (2)
【分析】(1)根据得,根据得,即,根据 即可证明;
(2)在中,以为底作为高,则,,根据 得,,即可得.
(1)证明:∵,
,
∵,
,
在和中,
,
;
(2)解:如图所示,在中,以为底作为高,
,,
∵,
,,
.
【点拨】本题考查了三角形的判定与性质,三角形的面积,解题的关键是理解题意,掌握这些知识点.
2 .已知:在和中,.
(1)如图①,若∠AOB=∠COD=60°,求证:AC=BD.
(2)如图②,若∠AOB=∠COD=α,则AC与BD间的等量关系式为__________,∠APB的大小为__________(直接写出结果,不证明)
【答案】(1)证明见解析
(2),α
【分析】(1)利用证明,即可得到结论;
(2)与(1)同理可证,得到,由得到,根据对顶角相等和三角形内角和定理得到即可.
【详解】(1)证明:∵,
∴,
∴.
在和中,,
∴,
∴;
(2)∵,
∴,
∴.
在和中,,
∴,
∴;
如图②,设与相交于点E,
∵,
∴,
在和中,
,,,
∴,
故答案为:,
【点评】此题考查了全等三角形的判定和性质、三角形内角和定理等知识,熟练掌握全等三角形的判定和性质是解题的关键.
题型训练
利用边角边判断边的数量关系
1.为参加学校举办的风筝设计比赛,小明用四根竹棒扎成如图所示的风筝框架,其中∠EDH=∠FDH,ED=FD.将上述条件标注在图中,小明不用测量就能知道EH=FH吗?为什么?
【解析】直接利用全等三角形的判定方法得出△HED≌△HFD(SAS),进而得出答案.
解:小明不用测量就能知道EH=FH.
理由:在△HED和△HFD中
∵,
∴△HED≌△HFD(SAS),
∴EH=FH.
2.小明在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆点O处用一根细绳悬挂一个小球A,小球A可以自由摆动,如图,OA表示小球静止时的位置.当小明用发声物体靠近小球时,小球从OA摆到OB位置,此时过点B作BD⊥OA于点D,当小球摆到OC位置时,OB与OC恰好垂直(图中的A、B、O、C在同一平面上),过点C作CE⊥OA于点E,测得CE=15cm,OE=8cm.
(1)试说明:OE=BD;
(2)求DE的长.
【解析】(1)利用AAS证明△COE≌△OBD,可得结论;
(2)利用全等三角形性质可得答案.
解:(1)∵OB⊥OC,
∴∠BOD+∠COE=90°,
∵CE⊥OA,BD⊥OA,
∴∠CEO=∠ODB=90°,
∴∠BOD+∠B=90°,
∴∠COE=∠B,
∵OC=BO,
∴△COE≌△OBD(AAS),
∴OE=BD;
(2)∵△COE≌△OBD,
∴CE=OD=15cm,
∴DE=OD-OE=7cm.
3.如图,AB=AE,BC=ED,∠B=∠E.
(1)求证:AC=AD.
(2)用直尺和圆规作图:过点A作AF⊥CD,垂足为F.(不写作法,保留作图痕迹)
【解析】(1)证明△ABC≌△AED(SAS),即可解决问题;
(2)根据等腰三角形的性质和尺规作图方法即可解决问题.
(1)证明:在△ABC和△AED中,
,
∴△ABC≌△AED(SAS),
∴AC=AD;
(2)解:如图AF即为所求.
利用边角边证明角相等
4.如图,已知AB平分∠CAD,AC=AD.求证:∠C=∠D.
【解析】根据角平分线的定义得到∠CAB=∠DAB,推出△ACB≌△ADB,根据全等三角形的性质即可得到结论.
证明:∵AB平分∠CAD,
∴∠CAB=∠DAB,
在△ACB与△ADB中,
,
∴△ACB≌△ADB(SAS),
∴∠C=∠D.
5.已知:如图,AB∥DE,AB=DE,AF=DC.求证:∠B=∠E.
【解析】由AF=DC,得AC=DF,由AB∥DE,得∠A=∠D,即可证△ABC≌△DEF(SAS),故∠B=∠E.
证明:∵AF=DC,
∴AF+CF=DC+CF,即AC=DF,
∵AB∥DE,
∴∠A=∠D,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠B=∠E.
利用边角边求角的度数
6.如图,点,分别是边长为的等边的边,上的动点,点从点向点运动,点从点向点运动,它们同时出发,且速度都为,运动的时间为秒,连接,交于点,则在,运动的过程中,
(1)求证:;
(2)的大小变化吗?若变化,则说明理由,若不变,则求出它的度数;
【答案】(1)见解析 (2)不变,
【解析】(1)根据等边三角形的性质得出,,根据点,的运动速度相等,得出,即可证明;
(2)由(1)得,根据三角形的外角的性质,即可求解.
【小问1详解】
证明:∵是等边三角形,
∴,,
∵点、的速度相同,
∴,
在和中
∴;
【小问2详解】
解:的大小不发生变化,
∵,
∴,
∴
;
【点睛】本题考查了等边三角形的性质,三角形外角的性质,全等三角形的性质与判定,掌握以上知识是解题的关键.
7.如图,在 ABC中,BE,CF分别是AC,AB边上的高,在BE上取一点D,使DB=AC,在射线CF上取一点G,使GC=AB,连结AG,AD.若∠DAE=38°,∠ABE,则∠G的度数为 .
【答案】32度/
【分析】证明得到,根据三角形的内角和定理求得即可.
【详解】解:,分别是,边上的高,
.
,.
.
在和中,,,,
.
.
,
.
【点睛】本题考查三角形的高、全等三角形得判定与性质、三角形的内角和定理,证明是解答的关键.
综合边边边、边角边进行计算证明
8.已知四边形中,,,如图2,点P,Q分别在线段,上,满足,求证:.
证明见分析
【分析】在的延长线上取点K,使得,连接,根据四边形内角和,证明,得到,,再证明,得到,进而推出,然后结合,即可证明结论.
解:证明:如图,在的延长线上取点K,使得,连接,
,
,
,
,
在和中,
,
,
,,
,
,
在和中,
,
,
,
,
,
,
,
,
,
.
【点拨】本题考查了全等三角形的判定和性质,四边形内角和,做辅助线构造全等三角形是解题关键.
牛刀小试
一、单选题(每小题4分,共32分)
1.如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
答案:C
解析:在和中
,,
当时,满足,可证明,故选项A符合题意;
当时,满足,可证明,故选项B符合题意;
当时,满足,不能证明,故选项C不符合题意;
当时,满足,可证明,故选项D符合题意;
故选:C.
2.如图,已知,添加一个条件,使得,下列条件添加错误的是( )
A. B. C. D.
答案:B
解析:A、在和中
,
,故本选项不符合题意;
B、,,不能推,故本选项符合题意;
C、在和中
,
,故本选项不符合题意;
D、在和中
,
,故本选项不符合题意;
故选:B.
3.如图,在与中,,,,,AB交EF于点D,连接EB.下列结论:
①;
②;
③;
④,正确的个数为( )
A.4个 B.3个 C.2个 D.1个
答案:B
解析:在和中,
,
,
,,,故②正确,
,
,故①正确,
,
,故③正确,
无法证明,故④错误,
综上,①②③正确,
故选:B.
4.我国的纸伞工艺十分巧妙,如图,伞圈D能沿着伞柄滑动,伞不论张开还是缩拢,伞柄始终平分同一平面内所成的角,为了证明这个结论,我们的依据是( )
A. B. C. D.
答案:B
解析:根据伞的结构,,伞骨,是公共边,
在和中,
,
,
即平分.
故选:B.
5.如图,在和中,,,要使,则可以添加下列哪个条件( )
A. B. C. D.
答案:C
解析:,,即,又,
A.添加,不能推出,不符合题意;
B.添加,不能推出,不符合题意;
C.添加,可得,利用可推出,符合题意;
D.添加,可得,但不能推出,不符合题意.
故选:C.
6.根据下列图中所给定的条件,找出全等的三角形( )
A.①和② B.②和③ C.①和③ D.①和④
答案:D
解析:①和④符合了,
①和④两个三角形全等.
故选:D.
7.如图,,要使,还需添加一个条件是( )
A. B. C. D.
答案:B
解析:,
,
又AE公共边,
当时,无法证明,故A不符合题意;
当时,利用SAS证明,故B符合题意;
当时,无法证明,故C不符合题意;
当时,无法证明,故D不符合题意;
故选:B.
如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点均在小正方形方格的顶点上,线段交于点,若,则等于( )
A. B. C. D.
【答案】C
【分析】根据三角形外角的性质及平行线的性质可进行求解.
解:如图,
由图可知:,,
∴,
∴,
∵,
∴,
∵,
∴,
∴;
故选C.
【点拨】本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
二、填空题(每小题4分,共20分)
9.如图,A,B两点分别位于一个池塘的两端,小凡想用绳子测量A,B间的距离,但无法从A点直接到达B点,聪明的小凡想出一个办法:先在地上选取一个可以直接到达B点的点C,连接BC,取BC的中点P(点P可以直接到达A点),连接AP并延长到点D,使DP=AP.连接CD,并测量出它的长度为10米,则A,B两点间的距离为 _____米.
【答案】10
【解析】由题意知AP=DP,BP=CP,根据SAS定理证明△ABC≌△DEC,即可得AB=DE,即可求得结果.
解:由题意知AP=DP,BP=CP,且∠APB=∠DPC,
在△ABP和△DCP中,
,
∴ABP≌△DCP(SAS),
∴AB=DE,
∵DE=10米,
∴AB=10米.
故答案为:10.
10.“三月三,放风筝”,如图是小明制作的风筝,他根据DE=DF,EH=FH,不用测量,就知道∠DEH=∠DFH,小明是通过全等三角形的知识得到的结论,则小明判定三角形全等的依据是_____(用字母表示).
【答案】SSS
【解析】根据SSS即可证明△DHE≌△DHF,可得∠DEH=∠DFH.
解:在△DHE和△DHF中,
,
∴△DHE≌△DHF(SSS),
∴∠DEH=∠DFH.
故答案为:SSS.
11.如图所示.A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1km,DC=1km,村庄AC,AD间也有公路相连,且公路AD是南北走向,AC=3km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2km,BF=0.7km.试求建造的斜拉桥长至少有___________km.
【答案】1.1
【解析】根据BD=CD,∠BDA=∠CDA=90°,AD=AD,得出△ADB≌△ADC,进而得出AB=AC=3,这样可得出斜拉桥长度.
解:由题意知:BD=CD,∠BDA=∠CDA=90°,
∵在△ADB和△ADC中,
,
∴△ADB≌△ADC(SAS),
∴AB=AC=3km,
故斜拉桥至少有3-1.2-0.7=1.1(km).
故答案为:1.1.
12.如图,一块三角形玻璃裂成①②两块,现需配一块同样的玻璃,为方便起见,只需带上碎片_____即可.
【答案】②
【解析】此题实际上考查全等三角形的应用,②中两边及其夹角,进而可确定其形状.
解:②中满足两边夹一角完整,即可得到一个与原来三角形全等的新三角形,所以只需带②去即可.
故答案为:②.
13.如图,在△ABC中,AB=AC,D为BC上的一点,∠BAD=28°,在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE,DE,DE交AC于点O,若CE∥AB,则∠DOC的度数为 _____.
【答案】92°
【解析】根据已知条件证明△DAB≌△EAC,可得∠B=∠ACE,再根据CE∥AB,可得∠B+∠ACB+∠ACE=180°,然后证明△ABC是等边三角形,△ADE是等边三角形,进而根据三角形内角和定理即可解决问题.
解:∵∠DAE=∠BAC,
∴∠DAE-∠DAC=∠BAC-∠DAC,
∴∠DAB=∠EAC,
在△DAB和△EAC中,
,
∴△DAB≌△EAC(SAS),
∴∠B=∠ACE,
∵CE∥AB,
∴∠B+∠BCE=180°,
∴∠B+∠ACB+∠ACE=180°,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠ACB=∠ACE=60°,
∴△ABC是等边三角形,
∴∠DAE=∠BAC=60°,
∴△ADE是等边三角形,
∴∠ADE=60°,
∵∠BAD=28°,
∴∠OAD=60°-28°=32°,
∴∠DOC=∠OAD+∠ADE=32°+60°=92°.
故答案为:92°.
三、解答题(共6小题,共48分)
14.(8分)(1)萧县某中学计划为学生暑期军训配备如图(1)所示的折叠凳,这样设计的折叠凳坐着舒适、稳定.这种设计所运用的数学原理是 _____;
(2)图(2)是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,交点O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为38cm,则由以上信息可推得CB的长度是多少?请说明理由.
【答案】三角形具有稳定性.
【解析】(1)根据三角形的稳定性进行解答即可;
(2)证明△AOD≌△BOC(SAS),得BC=AD,结合已知条件则可知BC的长度
解:(1)由题意得,这种设计所运用的数学原理是三角形具有稳定性;
故答案为:三角形具有稳定性.
(2)CB=38cm.
理由如下:∵O是AB和CD的中点,
∴AO=BO,CO=DO,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
又∵AD=38cm,
∴BC=AD=38cm.
15.(8分)如图,AB=AC,D为△ABC内部一点,且BD=CD.连接AD并延长,交BC于点E.
①请写出图中两组全等的三角形;
②任选其一说明全等的理由.
【解析】①利用全等三角形的判定定理可得结论;
②△ABD≌△ACD;利用SSS定理证明即可.
解:①△ABD≌△ACD,△ABE≌△ACE,
△BDE≌△CDE(写出两组即可);
②△ABD≌△ACD;
理由:在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS).
16.(8分)已知如图,在四边形ABCD中,AB=CD,AD=BC,求证:∠A=∠C.
【解析】连接AC,证明△ABC≌△CDA
证明:连接AC∵△ABC和△CDA中,
∴△ABC和△CDA
17.(8分)如图,等腰梯形ABCD中,AD∥BC,P为等腰梯形内部一点,若PA=PD,试说明PB=PC.
【解析】先根据已知求得∠BAP=∠CDP,再利用SAS判定△ABP≌△DCP从而得出PB=PC.
证明:∵四边形ABCD是等腰梯形,且AD∥BC,
∴∠BAD=∠CDA,AB=DC.
∵PA=PD,
∴∠PAD=∠PDA.
∴∠BAP=∠CDP.
在△ABP和△DCP中,,
∴△ABP≌△DCP.
∴PB=PC.
18 .(8分)如图,在 ABC中,∠B=50°,∠C=20°.过点A作AE⊥BC,垂足为E,延长EA至点D.使AD=AC.在边AC上截取AF=AB,连接DF.求证:DF=CB.
【答案】见解析
【分析】利用三角形内角和定理得的度数,再根据全等三角形的判定与性质可得结论.
【详解】证明:在 中,,,
.
.
.
,
.
在和中,
,
∴.
.
【点评】此题考查的是全等三角形的判定与性质,掌握其性质定理是解决此题的关键.
19 .(10分)问题发现:如图1,已知C为线段AB上一点,分别以线段AC,BC为直角边作等腰直角三角形,∠ACD=90°,CA=CD,CB=CE,连接AE,BD,线段AE,BD之间的数量关系为______;位置关系为_______.
拓展探究:如图2,把Rt ACD绕点C逆时针旋转,线段AE,BD交于点F,则AE与BD之间的关系是否仍然成立?请说明理由.
【答案】问题发现:,;拓展探究:成立,理由见解析
【分析】问题发现:根据题目条件证△ACE≌△DCB,再根据全等三角形的性质即可得出答案;
拓展探究:用SAS证,根据全等三角形的性质即可证得.
【详解】解:问题发现:延长BD,交AE于点F,如图所示:
∵,
∴,
又∵,
∴(SAS),
,
∵,
∴,
∴,
∴,
,
故答案为:,;
拓展探究:成立.
理由如下:设与相交于点,如图1所示:
∵,
∴,
又∵,,
∴(SAS),
∴,,
∵,
∴,
∴,
∴,
即,依然成立.
【点评】本题考查全等三角形的判定和性质,三角形三边关系,手拉手模型,熟练掌握全等三角形的判定和手拉手模型是解决本题的关键.
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.2 三角形全等的判定2
学习目标
1.能够利用尺规正确的画出一个与给定三角形满足SAS条件的全等的三角形,能准确叙述SAS.
2.能够利用SAS进行简单的几何推理(计算或证明)
3.能够利用SAS进行较复杂的几何推理(计算或证明)
4.能画图说明满足SSA条件的两个三角形不一定全等.能够综合利用SSS、SAS进行复杂的几何推理.
老师告诉你
倍长中线法:
遇到三角形的中线(中点)问题时,常将中线延长一倍(这种方法称倍长中线法),然后连接相应的顶点,构造全等三角形,通过全等三角形的性质将线段的关系进行转化,从而达到解决问题的目的。
知识点拨
知识点1 全等三角形的判定2:边角边(SAS)
三角形全等的判定2:边角边(SAS)
文字:在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等;
图形:
符号:在与中,.
【新知导学】
例1-1.生活中,我们在测量一个小口圆形容器内径时,常借用某些特制工具测量.如图所示,小青同学将钢条AD和钢条BC的中点O焊接在一起,制作了一把“X型卡钳”.小青同学测量出AB的长度时,就知道内径CD的长度.根据以上信息,你明白其中涉及的全等知识是( )
A. SSS B. AAS C. SAS D. ASA
【对应导练】
1.如图,为了测出池塘两端A,B间的距离,小依在地面上取一个可以直接到达A点和B点的点O,连接AO并延长到C,使OC=OA;连接BO并延长到D,使OD=OB,连接CD并测量出它的长度.小铱认为CD的长度就是A,B间的距离,她是根据△OAB≌△OCD来判断的AB=CD,那么判定这两个三角形全等的依据是( )
A. sss B. SAS C. ASA D. AAS
2.如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC上一点,连接AD.过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F.若BE=4,CF=1,则EF的长度为 _____.
3.如图,D,E分别是等边三角形ABC的边AC、AB上的点,,,则________.
知识点2 利用SAS进行推理证明
①用“SAS”判定两个三角形全等时,必须满足“两边及它们的夹角”这一条件,在书写时,一般按“边角边”的顺序.
②有两边和其中一角对应相等的两个三角形不一定全等
【新知导学】
例2-1.如图,在△ABC中,点D在BC的延长线上,DE∥AC,且DE=BC,AC=BD.求证:△ABC≌△BED.
【对应导练】
1.如图,AB=AC,∠BAD=∠CAD,证明:△ABD≌△ACD.
2.如图,AF=DC,∠BCA=∠EFD,BC=EF,求证:△ABC≌△DEF.
3.如图,△ABC和△BDE是等边三角形,连接AD、CE.求证:△ABD≌△CBE.
知识点3 综合利用SSS、SAS进行复杂的几何推理.
证明三角形全等的“两个条件”(1)直接条件:已知中直接给出的边(角)对应相等,
隐含条件:已知中没有给出,但通过读图得到的条件,如公共边、公共角、对顶角。
“SAS”判定方法证明两个三角形全等及进行简单的应用.
1.证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.
2判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
【新知导学】
例3-1 .如图,在四边形中对角线、交于点E,给出下列三组等量关系:①;②,③;请选择其中两组等量关系作为已知条件,另一组等量关系作为结论,并写出说理过程.
【对应导练】
如图,点A,B,C,D在同一条直线上,,,.
求证:;
若,求三角形的面积.
2 .已知:在和中,.
(1)如图①,若∠AOB=∠COD=60°,求证:AC=BD.
(2)如图②,若∠AOB=∠COD=α,则AC与BD间的等量关系式为__________,∠APB的大小为__________(直接写出结果,不证明)
题型训练
利用边角边判断边的数量关系
1.为参加学校举办的风筝设计比赛,小明用四根竹棒扎成如图所示的风筝框架,其中∠EDH=∠FDH,ED=FD.将上述条件标注在图中,小明不用测量就能知道EH=FH吗?为什么?
2.小明在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆点O处用一根细绳悬挂一个小球A,小球A可以自由摆动,如图,OA表示小球静止时的位置.当小明用发声物体靠近小球时,小球从OA摆到OB位置,此时过点B作BD⊥OA于点D,当小球摆到OC位置时,OB与OC恰好垂直(图中的A、B、O、C在同一平面上),过点C作CE⊥OA于点E,测得CE=15cm,OE=8cm.
(1)试说明:OE=BD;
(2)求DE的长.
3.如图,AB=AE,BC=ED,∠B=∠E.
(1)求证:AC=AD.
(2)用直尺和圆规作图:过点A作AF⊥CD,垂足为F.(不写作法,保留作图痕迹)
利用边角边证明角相等
4.如图,已知AB平分∠CAD,AC=AD.求证:∠C=∠D.
5.已知:如图,AB∥DE,AB=DE,AF=DC.求证:∠B=∠E.
利用边角边求角的度数
6.如图,点,分别是边长为的等边的边,上的动点,点从点向点运动,点从点向点运动,它们同时出发,且速度都为,运动的时间为秒,连接,交于点,则在,运动的过程中,
(1)求证:;
(2)的大小变化吗?若变化,则说明理由,若不变,则求出它的度数;
7.如图,在 ABC中,BE,CF分别是AC,AB边上的高,在BE上取一点D,使DB=AC,在射线CF上取一点G,使GC=AB,连结AG,AD.若∠DAE=38°,∠ABE,则∠G的度数为 .
综合边边边、边角边进行计算证明
8.已知四边形中,,,如图2,点P,Q分别在线段,上,满足,求证:.
牛刀小试
一、单选题(每小题4分,共32分)
1.如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
2.如图,已知,添加一个条件,使得,下列条件添加错误的是( )
A. B. C. D.
3.如图,在与中,,,,,AB交EF于点D,连接EB.下列结论:
①;
②;
③;
④,正确的个数为( )
A.4个 B.3个 C.2个 D.1个
4.我国的纸伞工艺十分巧妙,如图,伞圈D能沿着伞柄滑动,伞不论张开还是缩拢,伞柄始终平分同一平面内所成的角,为了证明这个结论,我们的依据是( )
A. B. C. D.
5.如图,在和中,,,要使,则可以添加下列哪个条件( )
A. B. C. D.
6.根据下列图中所给定的条件,找出全等的三角形( )
A.①和② B.②和③ C.①和③ D.①和④
7.如图,,要使,还需添加一个条件是( )
A. B. C. D.
如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点均在小正方形方格的顶点上,线段交于点,若,则等于( )
A. B. C. D.
二、填空题(每小题4分,共20分)
9.如图,A,B两点分别位于一个池塘的两端,小凡想用绳子测量A,B间的距离,但无法从A点直接到达B点,聪明的小凡想出一个办法:先在地上选取一个可以直接到达B点的点C,连接BC,取BC的中点P(点P可以直接到达A点),连接AP并延长到点D,使DP=AP.连接CD,并测量出它的长度为10米,则A,B两点间的距离为 _____米.
10.“三月三,放风筝”,如图是小明制作的风筝,他根据DE=DF,EH=FH,不用测量,就知道∠DEH=∠DFH,小明是通过全等三角形的知识得到的结论,则小明判定三角形全等的依据是_____(用字母表示).
11.如图所示.A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1km,DC=1km,村庄AC,AD间也有公路相连,且公路AD是南北走向,AC=3km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2km,BF=0.7km.试求建造的斜拉桥长至少有___________km.
12.如图,一块三角形玻璃裂成①②两块,现需配一块同样的玻璃,为方便起见,只需带上碎片_____即可.
13.如图,在△ABC中,AB=AC,D为BC上的一点,∠BAD=28°,在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE,DE,DE交AC于点O,若CE∥AB,则∠DOC的度数为 _____.
三、解答题(共6小题,共48分)
14.(8分)(1)萧县某中学计划为学生暑期军训配备如图(1)所示的折叠凳,这样设计的折叠凳坐着舒适、稳定.这种设计所运用的数学原理是 _____;
(2)图(2)是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,交点O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为38cm,则由以上信息可推得CB的长度是多少?请说明理由.
15.(8分)如图,AB=AC,D为△ABC内部一点,且BD=CD.连接AD并延长,交BC于点E.
①请写出图中两组全等的三角形;
②任选其一说明全等的理由.
16.(8分)已知如图,在四边形ABCD中,AB=CD,AD=BC,求证:∠A=∠C.
17.(8分)如图,等腰梯形ABCD中,AD∥BC,P为等腰梯形内部一点,若PA=PD,试说明PB=PC.
18 .(8分)如图,在 ABC中,∠B=50°,∠C=20°.过点A作AE⊥BC,垂足为E,延长EA至点D.使AD=AC.在边AC上截取AF=AB,连接DF.求证:DF=CB.
19 .(10分)问题发现:如图1,已知C为线段AB上一点,分别以线段AC,BC为直角边作等腰直角三角形,∠ACD=90°,CA=CD,CB=CE,连接AE,BD,线段AE,BD之间的数量关系为______;位置关系为_______.
拓展探究:如图2,把Rt ACD绕点C逆时针旋转,线段AE,BD交于点F,则AE与BD之间的关系是否仍然成立?请说明理由.
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.2 三角形全等的判定2
学习目标
1.能够利用尺规正确的画出一个与给定三角形满足SAS条件的全等的三角形,能准确叙述SAS.
2.能够利用SAS进行简单的几何推理(计算或证明)
3.能够利用SAS进行较复杂的几何推理(计算或证明)
4.能画图说明满足SSA条件的两个三角形不一定全等.能够综合利用SSS、SAS进行复杂的几何推理.
老师告诉你
倍长中线法:
遇到三角形的中线(中点)问题时,常将中线延长一倍(这种方法称倍长中线法),然后连接相应的顶点,构造全等三角形,通过全等三角形的性质将线段的关系进行转化,从而达到解决问题的目的。
知识点拨
知识点1 全等三角形的判定2:边角边(SAS)
三角形全等的判定2:边角边(SAS)
文字:在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等;
图形:
符号:在与中,.
【新知导学】
例1-1.生活中,我们在测量一个小口圆形容器内径时,常借用某些特制工具测量.如图所示,小青同学将钢条AD和钢条BC的中点O焊接在一起,制作了一把“X型卡钳”.小青同学测量出AB的长度时,就知道内径CD的长度.根据以上信息,你明白其中涉及的全等知识是( )
A. SSS B. AAS C. SAS D. ASA
【答案】C
【解析】根据全等三角形的判定定理即可得到结论.
解:在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
故选:C.
【对应导练】
1.如图,为了测出池塘两端A,B间的距离,小依在地面上取一个可以直接到达A点和B点的点O,连接AO并延长到C,使OC=OA;连接BO并延长到D,使OD=OB,连接CD并测量出它的长度.小铱认为CD的长度就是A,B间的距离,她是根据△OAB≌△OCD来判断的AB=CD,那么判定这两个三角形全等的依据是( )
A. sss B. SAS C. ASA D. AAS
【答案】B
【解析】由题意知OA=OC,OB=OD,由于∠AOB=∠COD,根据“SAS”即可证明△OAB≌△OCD.
解:由题意知OA=OC,OB=OD,
在△OAB和△OCD中,
,
∴△OAB≌△OCD(SAS).
故选:B.
2.如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC上一点,连接AD.过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F.若BE=4,CF=1,则EF的长度为 _____.
【答案】3
【解析】先证明△ABE≌△CAF(AAS),根据全等三角形的性质可得AF=BE=4,AE=CF=1,进一步可得EF的长.
解:∵BE⊥AD,CF⊥AD,
∴∠BEA=∠AFC=90°,
∴∠BAE+∠ABE=90°,
∵∠BAC=90°,
∴∠BAE+∠FAC=90°,
∴∠FAC=∠ABE,
在△ABE和△CAF中,
,
∴△ABE≌△CAF(AAS),
∴AF=BE,AE=CF,
∵BE=4,CF=1,
∴AF=BE=4,AE=CF=1,
∴EF=AF-AE=4-1=3,
故答案为:3.
3.如图,D,E分别是等边三角形ABC的边AC、AB上的点,,,则________.
【答案】
【解析】可证 可得∠ABD=∠BCE=15°由三角形外角即可计算∠BDC的度数.
解:在等边三角形ABC中:AB=BC,∠BAD=∠CBE=60°
∵
∴
∴∠ABD=∠BCE=15°
∴∠BDC=∠ABD+∠A=15°+60°=75°
故答案为75°
【点睛】本题考查了全等三角形的判定及应用,掌握三角形的判定是解题的关键.
知识点2 利用SAS进行推理证明
①用“SAS”判定两个三角形全等时,必须满足“两边及它们的夹角”这一条件,在书写时,一般按“边角边”的顺序.
②有两边和其中一角对应相等的两个三角形不一定全等
【新知导学】
例2-1.如图,在△ABC中,点D在BC的延长线上,DE∥AC,且DE=BC,AC=BD.求证:△ABC≌△BED.
【解析】根据平行线的性质得出∠D=∠ACB,再根据全等三角形的判定定理SAS推出即可.
证明:∵DE∥AC,
∴∠D=∠ACB,
在△ABC和△BED中,
,
∴△ABC≌△BED(SAS).
【对应导练】
1.如图,AB=AC,∠BAD=∠CAD,证明:△ABD≌△ACD.
【解析】根据“SAS”可判断△ABD≌△ACD.
证明:在△ABD和△ACD 中,
,
∴△ABD≌△ACD(SAS).
2.如图,AF=DC,∠BCA=∠EFD,BC=EF,求证:△ABC≌△DEF.
【解析】求出AC=DF,再根据全等三角形的判定定理SAS推出即可.
证明:∵AF=DC,
∴AF+FC=DC+CF,
即AC=DF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
3.如图,△ABC和△BDE是等边三角形,连接AD、CE.求证:△ABD≌△CBE.
【解析】根据等边三角形的性质得出AB=BC,BD=BE,进而利用SAS证明△ABD≌△CBE即可.
证明:∵△ABC,△BDE是等边三角形,
∴∠ABC=∠DBE=60°,AB=BC,BD=BE,
∴∠ABC-∠DBC=∠DBE-∠DBC,
∴∠ABD=∠CBE,
在△ABD和△CBE中,
,
∴△ABD≌△CBE(SAS).
知识点3 综合利用SSS、SAS进行复杂的几何推理.
证明三角形全等的“两个条件”(1)直接条件:已知中直接给出的边(角)对应相等,
隐含条件:已知中没有给出,但通过读图得到的条件,如公共边、公共角、对顶角。
“SAS”判定方法证明两个三角形全等及进行简单的应用.
1.证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.
2判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
【新知导学】
例3-1 .如图,在四边形中对角线、交于点E,给出下列三组等量关系:①;②,③;请选择其中两组等量关系作为已知条件,另一组等量关系作为结论,并写出说理过程.
答案:选择①③,证明②,证明见解析
解析:选择①③,证明②,
证明:在与中,
,
,
,
在与中,
,
,
,
.
【对应导练】
1.如图,点A,B,C,D在同一条直线上,,,.
求证:;
若,求三角形的面积.
【答案】(1) 见分析; (2)
【分析】(1)根据得,根据得,即,根据 即可证明;
(2)在中,以为底作为高,则,,根据 得,,即可得.
(1)证明:∵,
,
∵,
,
在和中,
,
;
(2)解:如图所示,在中,以为底作为高,
,,
∵,
,,
.
【点拨】本题考查了三角形的判定与性质,三角形的面积,解题的关键是理解题意,掌握这些知识点.
2 .已知:在和中,.
(1)如图①,若∠AOB=∠COD=60°,求证:AC=BD.
(2)如图②,若∠AOB=∠COD=α,则AC与BD间的等量关系式为__________,∠APB的大小为__________(直接写出结果,不证明)
【答案】(1)证明见解析
(2),α
【分析】(1)利用证明,即可得到结论;
(2)与(1)同理可证,得到,由得到,根据对顶角相等和三角形内角和定理得到即可.
【详解】(1)证明:∵,
∴,
∴.
在和中,,
∴,
∴;
(2)∵,
∴,
∴.
在和中,,
∴,
∴;
如图②,设与相交于点E,
∵,
∴,
在和中,
,,,
∴,
故答案为:,
【点评】此题考查了全等三角形的判定和性质、三角形内角和定理等知识,熟练掌握全等三角形的判定和性质是解题的关键.
题型训练
利用边角边判断边的数量关系
1.为参加学校举办的风筝设计比赛,小明用四根竹棒扎成如图所示的风筝框架,其中∠EDH=∠FDH,ED=FD.将上述条件标注在图中,小明不用测量就能知道EH=FH吗?为什么?
【解析】直接利用全等三角形的判定方法得出△HED≌△HFD(SAS),进而得出答案.
解:小明不用测量就能知道EH=FH.
理由:在△HED和△HFD中
∵,
∴△HED≌△HFD(SAS),
∴EH=FH.
2.小明在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆点O处用一根细绳悬挂一个小球A,小球A可以自由摆动,如图,OA表示小球静止时的位置.当小明用发声物体靠近小球时,小球从OA摆到OB位置,此时过点B作BD⊥OA于点D,当小球摆到OC位置时,OB与OC恰好垂直(图中的A、B、O、C在同一平面上),过点C作CE⊥OA于点E,测得CE=15cm,OE=8cm.
(1)试说明:OE=BD;
(2)求DE的长.
【解析】(1)利用AAS证明△COE≌△OBD,可得结论;
(2)利用全等三角形性质可得答案.
解:(1)∵OB⊥OC,
∴∠BOD+∠COE=90°,
∵CE⊥OA,BD⊥OA,
∴∠CEO=∠ODB=90°,
∴∠BOD+∠B=90°,
∴∠COE=∠B,
∵OC=BO,
∴△COE≌△OBD(AAS),
∴OE=BD;
(2)∵△COE≌△OBD,
∴CE=OD=15cm,
∴DE=OD-OE=7cm.
3.如图,AB=AE,BC=ED,∠B=∠E.
(1)求证:AC=AD.
(2)用直尺和圆规作图:过点A作AF⊥CD,垂足为F.(不写作法,保留作图痕迹)
【解析】(1)证明△ABC≌△AED(SAS),即可解决问题;
(2)根据等腰三角形的性质和尺规作图方法即可解决问题.
(1)证明:在△ABC和△AED中,
,
∴△ABC≌△AED(SAS),
∴AC=AD;
(2)解:如图AF即为所求.
利用边角边证明角相等
4.如图,已知AB平分∠CAD,AC=AD.求证:∠C=∠D.
【解析】根据角平分线的定义得到∠CAB=∠DAB,推出△ACB≌△ADB,根据全等三角形的性质即可得到结论.
证明:∵AB平分∠CAD,
∴∠CAB=∠DAB,
在△ACB与△ADB中,
,
∴△ACB≌△ADB(SAS),
∴∠C=∠D.
5.已知:如图,AB∥DE,AB=DE,AF=DC.求证:∠B=∠E.
【解析】由AF=DC,得AC=DF,由AB∥DE,得∠A=∠D,即可证△ABC≌△DEF(SAS),故∠B=∠E.
证明:∵AF=DC,
∴AF+CF=DC+CF,即AC=DF,
∵AB∥DE,
∴∠A=∠D,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠B=∠E.
利用边角边求角的度数
6.如图,点,分别是边长为的等边的边,上的动点,点从点向点运动,点从点向点运动,它们同时出发,且速度都为,运动的时间为秒,连接,交于点,则在,运动的过程中,
(1)求证:;
(2)的大小变化吗?若变化,则说明理由,若不变,则求出它的度数;
【答案】(1)见解析 (2)不变,
【解析】(1)根据等边三角形的性质得出,,根据点,的运动速度相等,得出,即可证明;
(2)由(1)得,根据三角形的外角的性质,即可求解.
【小问1详解】
证明:∵是等边三角形,
∴,,
∵点、的速度相同,
∴,
在和中
∴;
【小问2详解】
解:的大小不发生变化,
∵,
∴,
∴
;
【点睛】本题考查了等边三角形的性质,三角形外角的性质,全等三角形的性质与判定,掌握以上知识是解题的关键.
7.如图,在 ABC中,BE,CF分别是AC,AB边上的高,在BE上取一点D,使DB=AC,在射线CF上取一点G,使GC=AB,连结AG,AD.若∠DAE=38°,∠ABE,则∠G的度数为 .
【答案】32度/
【分析】证明得到,根据三角形的内角和定理求得即可.
【详解】解:,分别是,边上的高,
.
,.
.
在和中,,,,
.
.
,
.
【点睛】本题考查三角形的高、全等三角形得判定与性质、三角形的内角和定理,证明是解答的关键.
综合边边边、边角边进行计算证明
8.已知四边形中,,,如图2,点P,Q分别在线段,上,满足,求证:.
证明见分析
【分析】在的延长线上取点K,使得,连接,根据四边形内角和,证明,得到,,再证明,得到,进而推出,然后结合,即可证明结论.
解:证明:如图,在的延长线上取点K,使得,连接,
,
,
,
,
在和中,
,
,
,,
,
,
在和中,
,
,
,
,
,
,
,
,
,
.
【点拨】本题考查了全等三角形的判定和性质,四边形内角和,做辅助线构造全等三角形是解题关键.
牛刀小试
一、单选题(每小题4分,共32分)
1.如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
答案:C
解析:在和中
,,
当时,满足,可证明,故选项A符合题意;
当时,满足,可证明,故选项B符合题意;
当时,满足,不能证明,故选项C不符合题意;
当时,满足,可证明,故选项D符合题意;
故选:C.
2.如图,已知,添加一个条件,使得,下列条件添加错误的是( )
A. B. C. D.
答案:B
解析:A、在和中
,
,故本选项不符合题意;
B、,,不能推,故本选项符合题意;
C、在和中
,
,故本选项不符合题意;
D、在和中
,
,故本选项不符合题意;
故选:B.
3.如图,在与中,,,,,AB交EF于点D,连接EB.下列结论:
①;
②;
③;
④,正确的个数为( )
A.4个 B.3个 C.2个 D.1个
答案:B
解析:在和中,
,
,
,,,故②正确,
,
,故①正确,
,
,故③正确,
无法证明,故④错误,
综上,①②③正确,
故选:B.
4.我国的纸伞工艺十分巧妙,如图,伞圈D能沿着伞柄滑动,伞不论张开还是缩拢,伞柄始终平分同一平面内所成的角,为了证明这个结论,我们的依据是( )
A. B. C. D.
答案:B
解析:根据伞的结构,,伞骨,是公共边,
在和中,
,
,
即平分.
故选:B.
5.如图,在和中,,,要使,则可以添加下列哪个条件( )
A. B. C. D.
答案:C
解析:,,即,又,
A.添加,不能推出,不符合题意;
B.添加,不能推出,不符合题意;
C.添加,可得,利用可推出,符合题意;
D.添加,可得,但不能推出,不符合题意.
故选:C.
6.根据下列图中所给定的条件,找出全等的三角形( )
A.①和② B.②和③ C.①和③ D.①和④
答案:D
解析:①和④符合了,
①和④两个三角形全等.
故选:D.
7.如图,,要使,还需添加一个条件是( )
A. B. C. D.
答案:B
解析:,
,
又AE公共边,
当时,无法证明,故A不符合题意;
当时,利用SAS证明,故B符合题意;
当时,无法证明,故C不符合题意;
当时,无法证明,故D不符合题意;
故选:B.
如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点均在小正方形方格的顶点上,线段交于点,若,则等于( )
A. B. C. D.
【答案】C
【分析】根据三角形外角的性质及平行线的性质可进行求解.
解:如图,
由图可知:,,
∴,
∴,
∵,
∴,
∵,
∴,
∴;
故选C.
【点拨】本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
二、填空题(每小题4分,共20分)
9.如图,A,B两点分别位于一个池塘的两端,小凡想用绳子测量A,B间的距离,但无法从A点直接到达B点,聪明的小凡想出一个办法:先在地上选取一个可以直接到达B点的点C,连接BC,取BC的中点P(点P可以直接到达A点),连接AP并延长到点D,使DP=AP.连接CD,并测量出它的长度为10米,则A,B两点间的距离为 _____米.
【答案】10
【解析】由题意知AP=DP,BP=CP,根据SAS定理证明△ABC≌△DEC,即可得AB=DE,即可求得结果.
解:由题意知AP=DP,BP=CP,且∠APB=∠DPC,
在△ABP和△DCP中,
,
∴ABP≌△DCP(SAS),
∴AB=DE,
∵DE=10米,
∴AB=10米.
故答案为:10.
10.“三月三,放风筝”,如图是小明制作的风筝,他根据DE=DF,EH=FH,不用测量,就知道∠DEH=∠DFH,小明是通过全等三角形的知识得到的结论,则小明判定三角形全等的依据是_____(用字母表示).
【答案】SSS
【解析】根据SSS即可证明△DHE≌△DHF,可得∠DEH=∠DFH.
解:在△DHE和△DHF中,
,
∴△DHE≌△DHF(SSS),
∴∠DEH=∠DFH.
故答案为:SSS.
11.如图所示.A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1km,DC=1km,村庄AC,AD间也有公路相连,且公路AD是南北走向,AC=3km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2km,BF=0.7km.试求建造的斜拉桥长至少有___________km.
【答案】1.1
【解析】根据BD=CD,∠BDA=∠CDA=90°,AD=AD,得出△ADB≌△ADC,进而得出AB=AC=3,这样可得出斜拉桥长度.
解:由题意知:BD=CD,∠BDA=∠CDA=90°,
∵在△ADB和△ADC中,
,
∴△ADB≌△ADC(SAS),
∴AB=AC=3km,
故斜拉桥至少有3-1.2-0.7=1.1(km).
故答案为:1.1.
12.如图,一块三角形玻璃裂成①②两块,现需配一块同样的玻璃,为方便起见,只需带上碎片_____即可.
【答案】②
【解析】此题实际上考查全等三角形的应用,②中两边及其夹角,进而可确定其形状.
解:②中满足两边夹一角完整,即可得到一个与原来三角形全等的新三角形,所以只需带②去即可.
故答案为:②.
13.如图,在△ABC中,AB=AC,D为BC上的一点,∠BAD=28°,在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE,DE,DE交AC于点O,若CE∥AB,则∠DOC的度数为 _____.
【答案】92°
【解析】根据已知条件证明△DAB≌△EAC,可得∠B=∠ACE,再根据CE∥AB,可得∠B+∠ACB+∠ACE=180°,然后证明△ABC是等边三角形,△ADE是等边三角形,进而根据三角形内角和定理即可解决问题.
解:∵∠DAE=∠BAC,
∴∠DAE-∠DAC=∠BAC-∠DAC,
∴∠DAB=∠EAC,
在△DAB和△EAC中,
,
∴△DAB≌△EAC(SAS),
∴∠B=∠ACE,
∵CE∥AB,
∴∠B+∠BCE=180°,
∴∠B+∠ACB+∠ACE=180°,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠ACB=∠ACE=60°,
∴△ABC是等边三角形,
∴∠DAE=∠BAC=60°,
∴△ADE是等边三角形,
∴∠ADE=60°,
∵∠BAD=28°,
∴∠OAD=60°-28°=32°,
∴∠DOC=∠OAD+∠ADE=32°+60°=92°.
故答案为:92°.
三、解答题(共6小题,共48分)
14.(8分)(1)萧县某中学计划为学生暑期军训配备如图(1)所示的折叠凳,这样设计的折叠凳坐着舒适、稳定.这种设计所运用的数学原理是 _____;
(2)图(2)是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,交点O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为38cm,则由以上信息可推得CB的长度是多少?请说明理由.
【答案】三角形具有稳定性.
【解析】(1)根据三角形的稳定性进行解答即可;
(2)证明△AOD≌△BOC(SAS),得BC=AD,结合已知条件则可知BC的长度
解:(1)由题意得,这种设计所运用的数学原理是三角形具有稳定性;
故答案为:三角形具有稳定性.
(2)CB=38cm.
理由如下:∵O是AB和CD的中点,
∴AO=BO,CO=DO,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
又∵AD=38cm,
∴BC=AD=38cm.
15.(8分)如图,AB=AC,D为△ABC内部一点,且BD=CD.连接AD并延长,交BC于点E.
①请写出图中两组全等的三角形;
②任选其一说明全等的理由.
【解析】①利用全等三角形的判定定理可得结论;
②△ABD≌△ACD;利用SSS定理证明即可.
解:①△ABD≌△ACD,△ABE≌△ACE,
△BDE≌△CDE(写出两组即可);
②△ABD≌△ACD;
理由:在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS).
16.(8分)已知如图,在四边形ABCD中,AB=CD,AD=BC,求证:∠A=∠C.
【解析】连接AC,证明△ABC≌△CDA
证明:连接AC∵△ABC和△CDA中,
∴△ABC和△CDA
17.(8分)如图,等腰梯形ABCD中,AD∥BC,P为等腰梯形内部一点,若PA=PD,试说明PB=PC.
【解析】先根据已知求得∠BAP=∠CDP,再利用SAS判定△ABP≌△DCP从而得出PB=PC.
证明:∵四边形ABCD是等腰梯形,且AD∥BC,
∴∠BAD=∠CDA,AB=DC.
∵PA=PD,
∴∠PAD=∠PDA.
∴∠BAP=∠CDP.
在△ABP和△DCP中,,
∴△ABP≌△DCP.
∴PB=PC.
18 .(8分)如图,在 ABC中,∠B=50°,∠C=20°.过点A作AE⊥BC,垂足为E,延长EA至点D.使AD=AC.在边AC上截取AF=AB,连接DF.求证:DF=CB.
【答案】见解析
【分析】利用三角形内角和定理得的度数,再根据全等三角形的判定与性质可得结论.
【详解】证明:在 中,,,
.
.
.
,
.
在和中,
,
∴.
.
【点评】此题考查的是全等三角形的判定与性质,掌握其性质定理是解决此题的关键.
19 .(10分)问题发现:如图1,已知C为线段AB上一点,分别以线段AC,BC为直角边作等腰直角三角形,∠ACD=90°,CA=CD,CB=CE,连接AE,BD,线段AE,BD之间的数量关系为______;位置关系为_______.
拓展探究:如图2,把Rt ACD绕点C逆时针旋转,线段AE,BD交于点F,则AE与BD之间的关系是否仍然成立?请说明理由.
【答案】问题发现:,;拓展探究:成立,理由见解析
【分析】问题发现:根据题目条件证△ACE≌△DCB,再根据全等三角形的性质即可得出答案;
拓展探究:用SAS证,根据全等三角形的性质即可证得.
【详解】解:问题发现:延长BD,交AE于点F,如图所示:
∵,
∴,
又∵,
∴(SAS),
,
∵,
∴,
∴,
∴,
,
故答案为:,;
拓展探究:成立.
理由如下:设与相交于点,如图1所示:
∵,
∴,
又∵,,
∴(SAS),
∴,,
∵,
∴,
∴,
∴,
即,依然成立.
【点评】本题考查全等三角形的判定和性质,三角形三边关系,手拉手模型,熟练掌握全等三角形的判定和手拉手模型是解决本题的关键.
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
