人教版八年级数学上名师点拨精练第12章全等三角形12.2 三角形全等的判定3
文档属性
| 名称 | 人教版八年级数学上名师点拨精练第12章全等三角形12.2 三角形全等的判定3 |

|
|
| 格式 | doc | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-07 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.2 三角形全等的判定3
学习目标
1、掌握三角形全等的“角边角”“角角边”条件.能运用全等三角形的条件,解决简单的推理证明问题
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3、积极投入,激情展示,体验成功的快乐。
【学习重点】已知两角一边的三角形全等探究.
【学习难点】灵活运用三角形全等条件证明
老师告诉你
证明一条相等等于两条线段的和的方法-----截长法、补短法
截长法的基本思路就是在长线段上截取一段,使之等于其中一段,再证明剩下的线段等于另一短线段。
补短法的基本思路是延长短线段,使延长部分等于另一短线段,再证明延长后的线段等于长线段。
知识点拨
知识点1 判定三角形全等的方法---角边角 (ASA)
(1)两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
(2)书写格式:如图所示,在列举两个三角形全等的条件时,如:
在△ABC和△A′B′C′中,
∠A=∠A′
AB=A′B′
∠B=∠B′
∴△ABC≌△A′B′C′(SAS).
【新知导学】
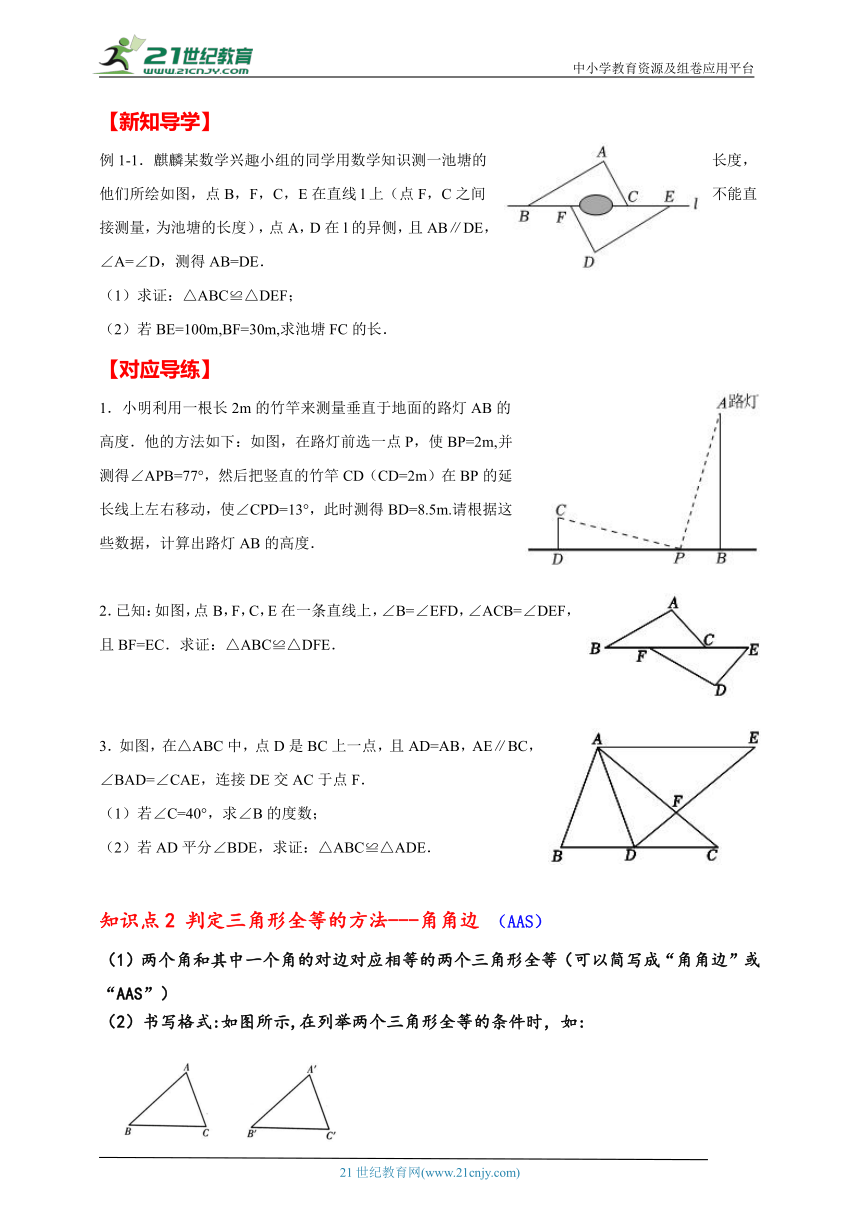
例1-1.麒麟某数学兴趣小组的同学用数学知识测一池塘的长度,他们所绘如图,点B,F,C,E在直线l上(点F,C之间不能直接测量,为池塘的长度),点A,D在l的异侧,且AB∥DE,∠A=∠D,测得AB=DE.
(1)求证:△ABC≌△DEF;
(2)若BE=100m,BF=30m,求池塘FC的长.
【对应导练】
1.小明利用一根长2m的竹竿来测量垂直于地面的路灯AB的高度.他的方法如下:如图,在路灯前选一点P,使BP=2m,并测得∠APB=77°,然后把竖直的竹竿CD(CD=2m)在BP的延长线上左右移动,使∠CPD=13°,此时测得BD=8.5m.请根据这些数据,计算出路灯AB的高度.
2.已知:如图,点B,F,C,E在一条直线上,∠B=∠EFD,∠ACB=∠DEF,且BF=EC.求证:△ABC≌△DFE.
3.如图,在△ABC中,点D是BC上一点,且AD=AB,AE∥BC,∠BAD=∠CAE,连接DE交AC于点F.
(1)若∠C=40°,求∠B的度数;
(2)若AD平分∠BDE,求证:△ABC≌△ADE.
知识点2 判定三角形全等的方法---角角边 (AAS)
(1)两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
(2)书写格式:如图所示,在列举两个三角形全等的条件时,如:
在△ABC和△A′B′C′中,
∠A=∠A′
∠B=∠B′
AC=A′C′
∴△ABC≌△A′B′C′(SAS).
由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.
【新知导学】
例2-1.如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠3,∠E=∠C,AE=AC,问△ABC≌△ADE吗?请说明理由.
【对应导练】
1.如图,点D,E在△ABC的边BC上,∠B=∠C,BD=CE,求证:△ABD≌△ACE.
2.如图,点B、F、C、E在同一条直线上,∠A=∠D,∠B=∠E,BF=CE,求证:△ABC≌△DEF.
3.已知:如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,且MS=PS.求证:△MNS≌△SQP.
知识点3判定方法的选择
1.选择哪种判定方法,要根据具体的已知条件而定,见下表:
已知条件 可选择的判定方法
一边一角对应相等 SAS AAS ASA
两角对应相等 ASA AAS
两边对应相等 SAS SSS
2.如何选择三角形证全等
(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;
(2)可以从已知出发,看已知条件确定证哪两个三角形全等;
(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;
(4)如果以上方法都行不通,就添加辅助线,构造全等三角形.
注意: 三个角对应相等的两个三角形不一定全等.
【新知导学】
例3-1.如图,BC=EC,∠1=∠2,添加一个适当的条件使△ABC≌△DEC,则需添加的条件是____________(不添加任何辅助线).
【对应导练】
1.如图,点B,E,C,F在一条直线上,BC=EF,∠B=∠DEF.只需添加一个条件即可证明△ABC≌△DEF,这个条件可以是 _____(写出一个即可).
2.如图,在△ABC和△FED中,AD=FC,∠A=∠F,请添加一个条件:_____,使△ABC≌△FED.
3.已知:如图,在△ABC和△DEF中,B,E,C,F在同一条直线上.下面四个条件:
①AB=DE;②AC=DF;③BE=CF;④∠ABC=∠DEF.
(1)请选择其中的三个条件,使得△ABC≌△DEF(写出一种情况即可).
(2)在(1)的条件下,求证:△ABC≌△DEF.
题型训练
1.利用角边角进行证明与计算
1.如图,点A、D、B、E在同一条直线上,若AD=BE,∠A=∠EDF,∠E=∠ABC求证:AC=DF.
2 .如图,AC//BD,AE,BE分别平分∠CAB和∠DBA,CD经过点E.求证:CE=DE.
2.利用角角边进行证明或计算
3 .如图,AB=AC,BE⊥AC于E,CD⊥AB于D,BE、CD交于点O,求证:OB=OC.
4 .(1)如图1,在等腰直角 ABC中,∠ACB=90°,AC=BC,过点C作直线DE,AD⊥DE于D,BE⊥DE于,求证:;
如图2,在等腰直角 ABC中,∠ACB=90°,AC=BC,过点C作直线CE,AD⊥DE于D,BE⊥DE于E ,AD=2.5cm,DF=2.7cm,求BE的长
(3)如图3,在平面直角坐标系中,A(-1,0),C(1,3), ABC为等腰直角三角形∠ACB=90°,AC=BC,求点B坐标.
截长补短法证明一条相等等于两条线段的和
5.已知中,,、是角平分线,他们相交于P,于P交的延长线于F,交于H.
(1)求的度数;
(2)求证:;
(3)连接,是否存在数m,使得?若存在,求出m;若不存在,说明理由.
6.综合与实践徐老师给爱好学习的小敏和小洁提出这样一个问题:如图1,在中,,是的平分线.
求证:.
(1)解决问题:小敏的证明思路:在上截取,连接.(如图2)
小洁的证明思路:延长至点E,使,连接.(如图3)
请你任意选择一种思路完成证明.
(2)问题升华:如图4,在中,若,,是外角的平分线,交的延长线于点D,则线段,,之间的数量关系又如何?请证明.
三、牛刀小试
一、单选题(每小题4分,共32分)
1.如图,在与中,点F在BC上,AB交EF于点D.,,,,则( )
A. B. C. D.
2.如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
3.如图,已知,添加一个条件,使得,下列条件添加错误的是( )
A. B. C. D.
4.如图,点E在AB上,点F在上,,,与BF相交点D,连接AD,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
5.如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.
A. B. C. D.和
6.的6个元素,如图所示,下面甲、乙、丙三个三角形中和全等的是( )
A.只有乙 B.只有丙 C.甲和乙 D.乙和丙
7.如图,在中,于点D,于点E,与交于点F,,则的长度为( )
A.10 B.6 C.5 D.4.5
8.如图,点O在AD上,,,,,,则OC的长为( )
A.2 B.3 C.4 D.6
二、填空题(每小题4分,共20分)
9.如图,已知,添加下列条件中的一个:①,②,③,其中不能确定的是_____(只填序号).
10.如图,在中,点D在AB边上,E是AC边的中点,,CF与DE的延长线交于点F,若,,则BD的长为_______.
11.如图,在由6个相同的小正方形拼成的网格中,______°.
12.如图,已知,要用“”说明,则需添加的一个条件是_____.
13.如图,已知,E为DF的中点,若,,则________cm.
三、解答题(共6小题,共48分)
14.(8分)如图,在中,,,于点E,且.求证:.
.
15.(8分)如图,与交于点O,,.求证:.
16.(8分)如图所示,在四边形ABCD中,,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
(1)判断FC与AD的数量关系,并说明理由;
(2)若,判断BE与AF的位置关系,并说明理由.
17(8分).如图,已知,,,求证:.
18.(8分)如图,四边中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
19.(8分)在练习课上,慧慧同学遇到了这样一道数学题:如图,把两个全等的直角三角板的斜边重合,组成一个四边形ACBD,,以D为顶点作,交边AC,BC于点M,N,,连接MN.
探究AM,MN,BN三条线段之间的数量关系.
慧慧分析:可先利用旋转,把其中的两条线段“接起来”,再通过证明两三角形全等,从而探究出AM,MN,BN三条线段之间的数量关系.
慧慧编题:在编题演练环节,慧慧编题如下:
如图(1),把两个全等的直角三角板的斜边重合,组成一个四边形,,以D为顶点作,交边AC,BC于点M,N,,连接MN.(1)先猜想AM,MN,BN三条线段之间的数量关系,再证明.(2)绕点D旋转,当M,N分别在CA,BC的延长线上,完成图(2),其余条件不变,直接写出AM,MN,BN三条线段之间的数量关系.
请你解答:请对慧慧同学所编制的问题进行解答.
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.2 三角形全等的判定3
学习目标
1、掌握三角形全等的“角边角”“角角边”条件.能运用全等三角形的条件,解决简单的推理证明问题
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3、积极投入,激情展示,体验成功的快乐。
【学习重点】已知两角一边的三角形全等探究.
【学习难点】灵活运用三角形全等条件证明
老师告诉你
证明一条相等等于两条线段的和的方法-----截长法、补短法
截长法的基本思路就是在长线段上截取一段,使之等于其中一段,再证明剩下的线段等于另一短线段。
补短法的基本思路是延长短线段,使延长部分等于另一短线段,再证明延长后的线段等于长线段。
知识点拨
知识点1 判定三角形全等的方法---角边角 (ASA)
(1)两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
(2)书写格式:如图所示,在列举两个三角形全等的条件时,如:
在△ABC和△A′B′C′中,
∠A=∠A′
AB=A′B′
∠B=∠B′
∴△ABC≌△A′B′C′(SAS).
【新知导学】
例1-1.麒麟某数学兴趣小组的同学用数学知识测一池塘的长度,他们所绘如图,点B,F,C,E在直线l上(点F,C之间不能直接测量,为池塘的长度),点A,D在l的异侧,且AB∥DE,∠A=∠D,测得AB=DE.
(1)求证:△ABC≌△DEF;
(2)若BE=100m,BF=30m,求池塘FC的长.
【解析】(1)先由平行线的性质得到∠ABC=∠DEF,再利用ASA证明△ABC≌△DEF即可;
(2)利用全等三角形的性质证明BF=EC,再结合已知条件即可得到答案.
(1)证明:∵AB∥DE,
∴∠ABC=∠DEF,
在△ABC与△DEF中,
∴△ABC≌DEF(ASA);
(2)解:∵△ABC≌△DEF,
∴BC=EF
∴BF+FC=EC+FC,
∴BF=EC,
∵BE=100m,BF=30m,
∴FC=100-30-30=40m.
答:FC的长是40m.
【对应导练】
1.小明利用一根长2m的竹竿来测量垂直于地面的路灯AB的高度.他的方法如下:如图,在路灯前选一点P,使BP=2m,并测得∠APB=77°,然后把竖直的竹竿CD(CD=2m)在BP的延长线上左右移动,使∠CPD=13°,此时测得BD=8.5m.请根据这些数据,计算出路灯AB的高度.
【解析】根据题意可得△CPD≌△PAB(ASA),进而利用AB=DP=DB-PB求出即可.
解:∵∠CPD=13°,∠APB=77°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=77°.
在△CPD和△PAB中,
,
∴△CPD≌△PAB(ASA).
∴DP=AB.
∵BD=8.5m,BP=2m,
∴DP=BD-BP=6.5m,即AB=6.5m.
答:路灯AB的高度是6.5m.
2.已知:如图,点B,F,C,E在一条直线上,∠B=∠EFD,∠ACB=∠DEF,且BF=EC.求证:△ABC≌△DFE.
【解析】首先求出BC=EF,进而利用全等三角形的判定定理ASA证明两个三角形全等.
解:∵BF=EC,
∴BF+CF=EC+CF,
∴BC=EF,
在△ABC和△DFE中,
,
∴△ABC △DFE(ASA).
3.如图,在△ABC中,点D是BC上一点,且AD=AB,AE∥BC,∠BAD=∠CAE,连接DE交AC于点F.
(1)若∠C=40°,求∠B的度数;
(2)若AD平分∠BDE,求证:△ABC≌△ADE.
【解析】(1)由AD=AB,得∠B=∠ADB.由AE∥BC,得∠EAC=∠C,那么∠C+∠DAC=∠EAC+∠DAC,即∠ADB=∠DAE.由∠BAD=∠CAE,得∠BAC=∠DAE,那么∠B=∠BAC.已知∠C=40°,根据三角形内角和定理求得∠B=70°.
(2)欲证AE=AC,可证△ABC≌△ADE.由AD平分∠BDE,得∠BDA=∠ADE,那么∠B=∠ADE.由∠BAD=∠CAE,得∠BAC=∠DAE,从而推断出△ABC≌△ADE.
(1)解:∵AD=AB,
∴∠B=∠ADB.
∵AE∥BC,
∴∠EAC=∠C.
又∵∠BAD=∠CAE,
∴∠BAD=∠C.
∵∠BDA=∠C+∠DAC,
∴∠BDA=∠BAD+∠DAC=∠BAC.
又∵∠B=∠BDA,
∴∠B=∠BAC.
∵∠C=40°,
∴∠B+∠BAC=180°-∠C=140°.
∴2∠B=140°.
∴∠B=70°.
(2)证明:由(1)得:∠B=∠ADB.
∵AD平分∠BDE,
∴∠BDA=∠ADE.
∴∠B=∠ADE.
∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC.
∴∠BAC=∠DAE.
在△ABC和△ADE中,
,
∴△ABC≌△ADE(ASA).
知识点2 判定三角形全等的方法---角角边 (AAS)
(1)两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
(2)书写格式:如图所示,在列举两个三角形全等的条件时,如:
在△ABC和△A′B′C′中,
∠A=∠A′
∠B=∠B′
AC=A′C′
∴△ABC≌△A′B′C′(SAS).
由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.
【新知导学】
例2-1.如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠3,∠E=∠C,AE=AC,问△ABC≌△ADE吗?请说明理由.
【解析】根据三角形的外角性质得出∠ADC=∠B+∠1,求出∠ADC=∠3+∠ADE,求出∠B=∠ADE,再根据全等三角形的判定定理AAS推出全等即可.
解:△ABC和△ADE全等,
理由是:∵∠ADC=∠B+∠1=∠3+∠ADE,
又∵∠1=∠3,
∴∠B=∠ADE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(AAS),
即△ABC和△ADE全等.
【对应导练】
1.如图,点D,E在△ABC的边BC上,∠B=∠C,BD=CE,求证:△ABD≌△ACE.
【解析】根据等角对等边可得AB=AC,然后利用SAS证明△ABD≌△ACE,即可解答.
证明:∵∠B=∠C,
∴AB=AC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS).
2.如图,点B、F、C、E在同一条直线上,∠A=∠D,∠B=∠E,BF=CE,求证:△ABC≌△DEF.
【解析】首先利用等式的性质求出BC=EF,进而利用全等三角形的判定定理AAS证明两个三角形全等.
证明:∵BF=CE,
∴BF+FC=CE+FC即BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
3.已知:如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,且MS=PS.求证:△MNS≌△SQP.
【解析】首先求出∠M=∠PSQ,进而利用AAS证明△MNS≌△SQP.
解:∵MS⊥PS,MN⊥SN,PQ⊥SN,
∴∠M+∠MSN=∠MSN+∠PSQ,
∴∠M=∠PSQ;
在△MNS与△SQP中,
,
∴△MNS≌△SQP(AAS).
知识点3判定方法的选择
1.选择哪种判定方法,要根据具体的已知条件而定,见下表:
已知条件 可选择的判定方法
一边一角对应相等 SAS AAS ASA
两角对应相等 ASA AAS
两边对应相等 SAS SSS
2.如何选择三角形证全等
(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;
(2)可以从已知出发,看已知条件确定证哪两个三角形全等;
(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;
(4)如果以上方法都行不通,就添加辅助线,构造全等三角形.
注意: 三个角对应相等的两个三角形不一定全等.
【新知导学】
例3-1.如图,BC=EC,∠1=∠2,添加一个适当的条件使△ABC≌△DEC,则需添加的条件是____________(不添加任何辅助线).
【答案】∠A=∠D(答案不唯一).
【解析】先说明∠ACB=∠DCE,再添加∠A=∠D,再结合BC=EC运用AAS即可证明△ABC≌△DEC.
解:添加条件:∠A=∠D;
∵∠1=∠2,
∴∠1+∠ECA=∠2+∠ECA即∠ACB=∠DCE
在△ABC和△DEC中
∠A=∠D ,∠ACB=∠DCE,BC=EC
∴△ABC≌△DEC(AAS).
故答案为:∠A=∠D(答案不唯一).
【点睛】本题考查了全等三角形的判定定理;掌握全等三角形的判定方法是解答本题的关键.
【对应导练】
1.如图,点B,E,C,F在一条直线上,BC=EF,∠B=∠DEF.只需添加一个条件即可证明△ABC≌△DEF,这个条件可以是 _____(写出一个即可).
【答案】AB=DE或∠A=∠D或∠ACB=∠DFE
【解析】根据“SAS”或“AAS”或“ASA”添加条件.
解:∵BC=EF,∠B=∠DEF.
∴当添加AB=DE时,根据“SAS”可判断△ABC≌△DEF;
当添加∠A=∠D时,根据“AAS”可判断△ABC≌△DEF;
当添加∠ACB=∠DFE时,根据“ASA”可判断△ABC≌△DEF;
故答案为:AB=DE或∠A=∠D或∠ACB=∠DFE.
2.如图,在△ABC和△FED中,AD=FC,∠A=∠F,请添加一个条件:_____,使△ABC≌△FED.
【答案】AB=FE或∠B=∠E或∠ACB=∠FDE或DE∥BC
【解析】根据三角形的判定定理:SSS、SAS、AAS进行判断即可.
解:∵AD=FC,
∴AC=FD,
∵∠A=∠F,
∴添加AB=FE,利用SAS得出△ABC≌△FED,
添加∠B=∠E,利用AAS得出△ABC≌△FED,
添加∠ACB=∠FDE,利用ASA得出△ABC≌△FED,
添加DE∥BC,得出∠EDF=∠BCA,利用ASA得出△ABC≌△FED,
故答案为:AB=FE或∠B=∠E或∠ACB=∠FDE或DE∥BC.
3.已知:如图,在△ABC和△DEF中,B,E,C,F在同一条直线上.下面四个条件:
①AB=DE;②AC=DF;③BE=CF;④∠ABC=∠DEF.
(1)请选择其中的三个条件,使得△ABC≌△DEF(写出一种情况即可).
(2)在(1)的条件下,求证:△ABC≌△DEF.
【解析】(1)根据两三角形全等的判定定理,选择合适的条件即可.
(2)根据(1)中所选条件,进行证明即可.
解:(1)由题知,
选择的三个条件是:①②③;
或者选择的三个条件是:①③④.
证明:(2)当选择①②③时,
∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS).
当选择①③④时,
∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
二、题型训练
1.利用角边角进行证明与计算
1.如图,点A、D、B、E在同一条直线上,若AD=BE,∠A=∠EDF,∠E=∠ABC求证:AC=DF.
【答案】见解析
【分析】由知,结合,,依据“”可判定≌,依据两三角形全等对应边相等可得.
【详解】证明:,
,即,
在和中,
,
,
.
【点评】本题主要考查全等三角形的判定与性质,掌握全等三角形的判定与性质是解题的关键.
2 .如图,AC//BD,AE,BE分别平分∠CAB和∠DBA,CD经过点E.求证:CE=DE.
【答案】证明见解析
【分析】在上截取,连接,通过证明和,然后根据全等三角形的性质分析求证.
【详解】证明:在上截取,连接.
∵,分别平分和,
∴.
∵,
∴,
在和中,
∴,
∴,
∵,
∴,
在和中,
∴,
∴,
∴.
【点评】本题考查全等三角形的判定和性质,通过添加辅助线构造全等三角形是解题关键.
2.利用角角边进行证明或计算
3 .如图,AB=AC,BE⊥AC于E,CD⊥AB于D,BE、CD交于点O,求证:OB=OC.
【分析】证△ABE≌△ACD,推出∠B=∠C,AD=AE,求出BD=CE,证△BDO≌△CEO,根据全等三角形的性质推出即可.
证明:∵BE⊥AC,CD⊥AB,
∴∠ADC=∠AEB=90°,
在△ABE和△ACD中
∴△ABE≌△ACD (AAS),
∴∠B=∠C,AD=AE,
∵AB=AC,
∴BD=CE,
在△BDO和△CEO中
∴△BDO≌△CEO (AAS),
∴OB=OC.
【点拨】本题考查了全等三角形的性质和判定的应用,主要考查学生的推理能力.
4 .(1)如图1,在等腰直角 ABC中,∠ACB=90°,AC=BC,过点C作直线DE,AD⊥DE于D,BE⊥DE于,求证:;
如图2,在等腰直角 ABC中,∠ACB=90°,AC=BC,过点C作直线CE,AD⊥DE于D,BE⊥DE于E ,AD=2.5cm,DF=2.7cm,求BE的长
(3)如图3,在平面直角坐标系中,A(-1,0),C(1,3), ABC为等腰直角三角形∠ACB=90°,AC=BC,求点B坐标.
【答案】(1)证明见解析
(2)
(3)
【分析】(1)由题意知,由,,可得,进而结论得证;
(2)同理(1)证明,则,,根据计算求解的值即可;
(3)如图3,过点作平行于轴的直线,过作于,过作于,由(1)可得,则,,进而可求点坐标.
【详解】(1)证明:∵,,
∴,
∵,,
∴,
在和中,
∵,
∴;
(2)解:∵,,
∴,
∵,,
∴,
在和中,
∵,
∴,
∴,,
∴,
∴的长为;
(3)解:如图3,过点作平行于轴的直线,过作于,过作于,
由(1)可得,
∴,,
∴.
【点评】本题考查了三角形内角和定理,全等三角形的判定与性质等知识.解题的关键在于证明三角形全等.
截长补短法证明一条相等等于两条线段的和
5.已知中,,、是角平分线,他们相交于P,于P交的延长线于F,交于H.
(1)求的度数;
(2)求证:;
(3)连接,是否存在数m,使得?若存在,求出m;若不存在,说明理由.
答案:(1)
(2)证明见解析
(3)存在,
解析:(1)证明:,
,
又、分别平分、,
,
.
(2),,
又,
,
,
在和中,
,
,
,
,
,
在和中,
,
,
,
又,
.
(3)存在..
理由:连接,,
,,
,,,
,
,
,
,
,
.
6.综合与实践徐老师给爱好学习的小敏和小洁提出这样一个问题:如图1,在中,,是的平分线.
求证:.
(1)解决问题:小敏的证明思路:在上截取,连接.(如图2)
小洁的证明思路:延长至点E,使,连接.(如图3)
请你任意选择一种思路完成证明.
(2)问题升华:如图4,在中,若,,是外角的平分线,交的延长线于点D,则线段,,之间的数量关系又如何?请证明.
答案:(1)见解析
(2)
解析:(1)小敏的证明思路:如图2,在上截取,连接.
是的平分线,
,
在与中,
,
,
,,
,,
,
,
.
小洁的证明思路:如图3,延长至点E,使,连接,则,
,
.
,
,
,
是的平分线,
.
,,,
,
,
.
(2)如图在的延长线上取一点E,使,连接,
平分,
在与中,
,
,
,,
,
,
,
,
,
,
.
三、牛刀小试
一、单选题(每小题4分,共32分)
1.如图,在与中,点F在BC上,AB交EF于点D.,,,,则( )
A. B. C. D.
答案:A
解析:,.在与中,,,.,,,.
2.如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
答案:C
解析:在和中
,,
当时,满足,可证明,故选项A符合题意;
当时,满足,可证明,故选项B符合题意;
当时,满足,不能证明,故选项C不符合题意;
当时,满足,可证明,故选项D符合题意;
故选:C.
3.如图,已知,添加一个条件,使得,下列条件添加错误的是( )
A. B. C. D.
答案:B
解析:A、在和中
,
,故本选项不符合题意;
B、,,不能推,故本选项符合题意;
C、在和中
,
,故本选项不符合题意;
D、在和中
,
,故本选项不符合题意;
故选:B.
4.如图,点E在AB上,点F在上,,,与BF相交点D,连接AD,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
答案:D
解析:,,,,,,.又,,,.,,,.又,,,由上可得,图中全等三角形共有4对.
5.如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.
A. B. C. D.和
答案:C
解析:A、第块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;
B、第块,仅保留了原三角形的一部分边,所以该块不行;
C、第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合判定,符合题意;
D、由上分析,和不符合题意;
故选:C.
6.的6个元素,如图所示,下面甲、乙、丙三个三角形中和全等的是( )
A.只有乙 B.只有丙 C.甲和乙 D.乙和丙
答案:D
解析:甲的边a,c的夹角和的边a,c的夹角不对应,故甲三角形与不全等;
甲的边a,c的夹角和的边a,c的夹角对应为,故可利用“边角边”证明乙三角形与全等;
丙的角,和边a与的角和边a对应,故可利用“角角边”证明丙三角形与全等,
甲、乙、丙三个三角形中和全等的是乙和丙,
故选:D.
7.如图,在中,于点D,于点E,与交于点F,,则的长度为( )
A.10 B.6 C.5 D.4.5
答案:C
解析: ,,
,
,,,
,
在和中,
,
,
,
;
故选:C.
8.如图,点O在AD上,,,,,,则OC的长为( )
A.2 B.3 C.4 D.6
答案:C
解析:,
,
,,
,
,,
,,
.
故选:C.
二、填空题(每小题4分,共20分)
9.如图,已知,添加下列条件中的一个:①,②,③,其中不能确定的是_____(只填序号).
答案:②
解析:已知,且,
若添加①,则可由判定;
若添加②,则属于边边角的顺序,不能判定;
若添加③,则属于边角边的顺序,可以判定.
故答案为②..
10.如图,在中,点D在AB边上,E是AC边的中点,,CF与DE的延长线交于点F,若,,则BD的长为_______.
答案:1
解析:,
,,
是AC的中点,
,
在与中,
,
,
,
,
故答案为:1.
11.如图,在由6个相同的小正方形拼成的网格中,______°.
答案:180
解析:,,,
,
,
.
故答案是:180.
12.如图,已知,要用“”说明,则需添加的一个条件是_____.
答案:
解析:添加条件.
在和中,,
,
故答案为:.
13.如图,已知,E为DF的中点,若,,则________cm.
答案:6
解析:,
,,
在和中
,
,
,
.
三、解答题(共6小题,共48分)
14.(8分)如图,在中,,,于点E,且.求证:.
答案:见解析
解析:证明:,,
,
,
,
在和中,
,
.
15.(8分)如图,与交于点O,,.求证:.
答案:见解析
解析:在和中,
,
,
16.(8分)如图所示,在四边形ABCD中,,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
(1)判断FC与AD的数量关系,并说明理由;
(2)若,判断BE与AF的位置关系,并说明理由.
答案:(1),理由见解析
(2),理由见解析
解析:(1)结论:.
理由:,
,
E是CD的中点,
,
在与中,
,
,
;
(2)结论:.
理由:由(1)知,
,,
,
,
即,
,
,
.
17(8分).如图,已知,,,求证:.
答案:见解析
解析:,
.
即,
在和中,
,
.
.
18.(8分)如图,四边中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
答案:(1)见解析
(2)3
解析:(1),
,
即:,
在和中,
,
,
;
(2),
,
,,
.
19.(8分)在练习课上,慧慧同学遇到了这样一道数学题:如图,把两个全等的直角三角板的斜边重合,组成一个四边形ACBD,,以D为顶点作,交边AC,BC于点M,N,,连接MN.
探究AM,MN,BN三条线段之间的数量关系.
慧慧分析:可先利用旋转,把其中的两条线段“接起来”,再通过证明两三角形全等,从而探究出AM,MN,BN三条线段之间的数量关系.
慧慧编题:在编题演练环节,慧慧编题如下:
如图(1),把两个全等的直角三角板的斜边重合,组成一个四边形,,以D为顶点作,交边AC,BC于点M,N,,连接MN.(1)先猜想AM,MN,BN三条线段之间的数量关系,再证明.(2)绕点D旋转,当M,N分别在CA,BC的延长线上,完成图(2),其余条件不变,直接写出AM,MN,BN三条线段之间的数量关系.
请你解答:请对慧慧同学所编制的问题进行解答.
答案:(1),证明见解析
(2),证明见解析
解析:(1),
证明:延长CB到E,使,连接DE,
,,,
,
,
,
,,
,
,
,,
在和中,
,
,
,,
,,
,
,
,
,
在和中,
,
,
,
,
,
(2),
证明:在CB截取,连接DE,
,,,
,
,,
,
,
,
,
,
在和中
,
,
,,
,
,
在和中,
,
,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.2 三角形全等的判定3
学习目标
1、掌握三角形全等的“角边角”“角角边”条件.能运用全等三角形的条件,解决简单的推理证明问题
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3、积极投入,激情展示,体验成功的快乐。
【学习重点】已知两角一边的三角形全等探究.
【学习难点】灵活运用三角形全等条件证明
老师告诉你
证明一条相等等于两条线段的和的方法-----截长法、补短法
截长法的基本思路就是在长线段上截取一段,使之等于其中一段,再证明剩下的线段等于另一短线段。
补短法的基本思路是延长短线段,使延长部分等于另一短线段,再证明延长后的线段等于长线段。
知识点拨
知识点1 判定三角形全等的方法---角边角 (ASA)
(1)两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
(2)书写格式:如图所示,在列举两个三角形全等的条件时,如:
在△ABC和△A′B′C′中,
∠A=∠A′
AB=A′B′
∠B=∠B′
∴△ABC≌△A′B′C′(SAS).
【新知导学】
例1-1.麒麟某数学兴趣小组的同学用数学知识测一池塘的长度,他们所绘如图,点B,F,C,E在直线l上(点F,C之间不能直接测量,为池塘的长度),点A,D在l的异侧,且AB∥DE,∠A=∠D,测得AB=DE.
(1)求证:△ABC≌△DEF;
(2)若BE=100m,BF=30m,求池塘FC的长.
【对应导练】
1.小明利用一根长2m的竹竿来测量垂直于地面的路灯AB的高度.他的方法如下:如图,在路灯前选一点P,使BP=2m,并测得∠APB=77°,然后把竖直的竹竿CD(CD=2m)在BP的延长线上左右移动,使∠CPD=13°,此时测得BD=8.5m.请根据这些数据,计算出路灯AB的高度.
2.已知:如图,点B,F,C,E在一条直线上,∠B=∠EFD,∠ACB=∠DEF,且BF=EC.求证:△ABC≌△DFE.
3.如图,在△ABC中,点D是BC上一点,且AD=AB,AE∥BC,∠BAD=∠CAE,连接DE交AC于点F.
(1)若∠C=40°,求∠B的度数;
(2)若AD平分∠BDE,求证:△ABC≌△ADE.
知识点2 判定三角形全等的方法---角角边 (AAS)
(1)两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
(2)书写格式:如图所示,在列举两个三角形全等的条件时,如:
在△ABC和△A′B′C′中,
∠A=∠A′
∠B=∠B′
AC=A′C′
∴△ABC≌△A′B′C′(SAS).
由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.
【新知导学】
例2-1.如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠3,∠E=∠C,AE=AC,问△ABC≌△ADE吗?请说明理由.
【对应导练】
1.如图,点D,E在△ABC的边BC上,∠B=∠C,BD=CE,求证:△ABD≌△ACE.
2.如图,点B、F、C、E在同一条直线上,∠A=∠D,∠B=∠E,BF=CE,求证:△ABC≌△DEF.
3.已知:如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,且MS=PS.求证:△MNS≌△SQP.
知识点3判定方法的选择
1.选择哪种判定方法,要根据具体的已知条件而定,见下表:
已知条件 可选择的判定方法
一边一角对应相等 SAS AAS ASA
两角对应相等 ASA AAS
两边对应相等 SAS SSS
2.如何选择三角形证全等
(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;
(2)可以从已知出发,看已知条件确定证哪两个三角形全等;
(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;
(4)如果以上方法都行不通,就添加辅助线,构造全等三角形.
注意: 三个角对应相等的两个三角形不一定全等.
【新知导学】
例3-1.如图,BC=EC,∠1=∠2,添加一个适当的条件使△ABC≌△DEC,则需添加的条件是____________(不添加任何辅助线).
【对应导练】
1.如图,点B,E,C,F在一条直线上,BC=EF,∠B=∠DEF.只需添加一个条件即可证明△ABC≌△DEF,这个条件可以是 _____(写出一个即可).
2.如图,在△ABC和△FED中,AD=FC,∠A=∠F,请添加一个条件:_____,使△ABC≌△FED.
3.已知:如图,在△ABC和△DEF中,B,E,C,F在同一条直线上.下面四个条件:
①AB=DE;②AC=DF;③BE=CF;④∠ABC=∠DEF.
(1)请选择其中的三个条件,使得△ABC≌△DEF(写出一种情况即可).
(2)在(1)的条件下,求证:△ABC≌△DEF.
题型训练
1.利用角边角进行证明与计算
1.如图,点A、D、B、E在同一条直线上,若AD=BE,∠A=∠EDF,∠E=∠ABC求证:AC=DF.
2 .如图,AC//BD,AE,BE分别平分∠CAB和∠DBA,CD经过点E.求证:CE=DE.
2.利用角角边进行证明或计算
3 .如图,AB=AC,BE⊥AC于E,CD⊥AB于D,BE、CD交于点O,求证:OB=OC.
4 .(1)如图1,在等腰直角 ABC中,∠ACB=90°,AC=BC,过点C作直线DE,AD⊥DE于D,BE⊥DE于,求证:;
如图2,在等腰直角 ABC中,∠ACB=90°,AC=BC,过点C作直线CE,AD⊥DE于D,BE⊥DE于E ,AD=2.5cm,DF=2.7cm,求BE的长
(3)如图3,在平面直角坐标系中,A(-1,0),C(1,3), ABC为等腰直角三角形∠ACB=90°,AC=BC,求点B坐标.
截长补短法证明一条相等等于两条线段的和
5.已知中,,、是角平分线,他们相交于P,于P交的延长线于F,交于H.
(1)求的度数;
(2)求证:;
(3)连接,是否存在数m,使得?若存在,求出m;若不存在,说明理由.
6.综合与实践徐老师给爱好学习的小敏和小洁提出这样一个问题:如图1,在中,,是的平分线.
求证:.
(1)解决问题:小敏的证明思路:在上截取,连接.(如图2)
小洁的证明思路:延长至点E,使,连接.(如图3)
请你任意选择一种思路完成证明.
(2)问题升华:如图4,在中,若,,是外角的平分线,交的延长线于点D,则线段,,之间的数量关系又如何?请证明.
三、牛刀小试
一、单选题(每小题4分,共32分)
1.如图,在与中,点F在BC上,AB交EF于点D.,,,,则( )
A. B. C. D.
2.如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
3.如图,已知,添加一个条件,使得,下列条件添加错误的是( )
A. B. C. D.
4.如图,点E在AB上,点F在上,,,与BF相交点D,连接AD,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
5.如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.
A. B. C. D.和
6.的6个元素,如图所示,下面甲、乙、丙三个三角形中和全等的是( )
A.只有乙 B.只有丙 C.甲和乙 D.乙和丙
7.如图,在中,于点D,于点E,与交于点F,,则的长度为( )
A.10 B.6 C.5 D.4.5
8.如图,点O在AD上,,,,,,则OC的长为( )
A.2 B.3 C.4 D.6
二、填空题(每小题4分,共20分)
9.如图,已知,添加下列条件中的一个:①,②,③,其中不能确定的是_____(只填序号).
10.如图,在中,点D在AB边上,E是AC边的中点,,CF与DE的延长线交于点F,若,,则BD的长为_______.
11.如图,在由6个相同的小正方形拼成的网格中,______°.
12.如图,已知,要用“”说明,则需添加的一个条件是_____.
13.如图,已知,E为DF的中点,若,,则________cm.
三、解答题(共6小题,共48分)
14.(8分)如图,在中,,,于点E,且.求证:.
.
15.(8分)如图,与交于点O,,.求证:.
16.(8分)如图所示,在四边形ABCD中,,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
(1)判断FC与AD的数量关系,并说明理由;
(2)若,判断BE与AF的位置关系,并说明理由.
17(8分).如图,已知,,,求证:.
18.(8分)如图,四边中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
19.(8分)在练习课上,慧慧同学遇到了这样一道数学题:如图,把两个全等的直角三角板的斜边重合,组成一个四边形ACBD,,以D为顶点作,交边AC,BC于点M,N,,连接MN.
探究AM,MN,BN三条线段之间的数量关系.
慧慧分析:可先利用旋转,把其中的两条线段“接起来”,再通过证明两三角形全等,从而探究出AM,MN,BN三条线段之间的数量关系.
慧慧编题:在编题演练环节,慧慧编题如下:
如图(1),把两个全等的直角三角板的斜边重合,组成一个四边形,,以D为顶点作,交边AC,BC于点M,N,,连接MN.(1)先猜想AM,MN,BN三条线段之间的数量关系,再证明.(2)绕点D旋转,当M,N分别在CA,BC的延长线上,完成图(2),其余条件不变,直接写出AM,MN,BN三条线段之间的数量关系.
请你解答:请对慧慧同学所编制的问题进行解答.
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.2 三角形全等的判定3
学习目标
1、掌握三角形全等的“角边角”“角角边”条件.能运用全等三角形的条件,解决简单的推理证明问题
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3、积极投入,激情展示,体验成功的快乐。
【学习重点】已知两角一边的三角形全等探究.
【学习难点】灵活运用三角形全等条件证明
老师告诉你
证明一条相等等于两条线段的和的方法-----截长法、补短法
截长法的基本思路就是在长线段上截取一段,使之等于其中一段,再证明剩下的线段等于另一短线段。
补短法的基本思路是延长短线段,使延长部分等于另一短线段,再证明延长后的线段等于长线段。
知识点拨
知识点1 判定三角形全等的方法---角边角 (ASA)
(1)两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
(2)书写格式:如图所示,在列举两个三角形全等的条件时,如:
在△ABC和△A′B′C′中,
∠A=∠A′
AB=A′B′
∠B=∠B′
∴△ABC≌△A′B′C′(SAS).
【新知导学】
例1-1.麒麟某数学兴趣小组的同学用数学知识测一池塘的长度,他们所绘如图,点B,F,C,E在直线l上(点F,C之间不能直接测量,为池塘的长度),点A,D在l的异侧,且AB∥DE,∠A=∠D,测得AB=DE.
(1)求证:△ABC≌△DEF;
(2)若BE=100m,BF=30m,求池塘FC的长.
【解析】(1)先由平行线的性质得到∠ABC=∠DEF,再利用ASA证明△ABC≌△DEF即可;
(2)利用全等三角形的性质证明BF=EC,再结合已知条件即可得到答案.
(1)证明:∵AB∥DE,
∴∠ABC=∠DEF,
在△ABC与△DEF中,
∴△ABC≌DEF(ASA);
(2)解:∵△ABC≌△DEF,
∴BC=EF
∴BF+FC=EC+FC,
∴BF=EC,
∵BE=100m,BF=30m,
∴FC=100-30-30=40m.
答:FC的长是40m.
【对应导练】
1.小明利用一根长2m的竹竿来测量垂直于地面的路灯AB的高度.他的方法如下:如图,在路灯前选一点P,使BP=2m,并测得∠APB=77°,然后把竖直的竹竿CD(CD=2m)在BP的延长线上左右移动,使∠CPD=13°,此时测得BD=8.5m.请根据这些数据,计算出路灯AB的高度.
【解析】根据题意可得△CPD≌△PAB(ASA),进而利用AB=DP=DB-PB求出即可.
解:∵∠CPD=13°,∠APB=77°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=77°.
在△CPD和△PAB中,
,
∴△CPD≌△PAB(ASA).
∴DP=AB.
∵BD=8.5m,BP=2m,
∴DP=BD-BP=6.5m,即AB=6.5m.
答:路灯AB的高度是6.5m.
2.已知:如图,点B,F,C,E在一条直线上,∠B=∠EFD,∠ACB=∠DEF,且BF=EC.求证:△ABC≌△DFE.
【解析】首先求出BC=EF,进而利用全等三角形的判定定理ASA证明两个三角形全等.
解:∵BF=EC,
∴BF+CF=EC+CF,
∴BC=EF,
在△ABC和△DFE中,
,
∴△ABC △DFE(ASA).
3.如图,在△ABC中,点D是BC上一点,且AD=AB,AE∥BC,∠BAD=∠CAE,连接DE交AC于点F.
(1)若∠C=40°,求∠B的度数;
(2)若AD平分∠BDE,求证:△ABC≌△ADE.
【解析】(1)由AD=AB,得∠B=∠ADB.由AE∥BC,得∠EAC=∠C,那么∠C+∠DAC=∠EAC+∠DAC,即∠ADB=∠DAE.由∠BAD=∠CAE,得∠BAC=∠DAE,那么∠B=∠BAC.已知∠C=40°,根据三角形内角和定理求得∠B=70°.
(2)欲证AE=AC,可证△ABC≌△ADE.由AD平分∠BDE,得∠BDA=∠ADE,那么∠B=∠ADE.由∠BAD=∠CAE,得∠BAC=∠DAE,从而推断出△ABC≌△ADE.
(1)解:∵AD=AB,
∴∠B=∠ADB.
∵AE∥BC,
∴∠EAC=∠C.
又∵∠BAD=∠CAE,
∴∠BAD=∠C.
∵∠BDA=∠C+∠DAC,
∴∠BDA=∠BAD+∠DAC=∠BAC.
又∵∠B=∠BDA,
∴∠B=∠BAC.
∵∠C=40°,
∴∠B+∠BAC=180°-∠C=140°.
∴2∠B=140°.
∴∠B=70°.
(2)证明:由(1)得:∠B=∠ADB.
∵AD平分∠BDE,
∴∠BDA=∠ADE.
∴∠B=∠ADE.
∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC.
∴∠BAC=∠DAE.
在△ABC和△ADE中,
,
∴△ABC≌△ADE(ASA).
知识点2 判定三角形全等的方法---角角边 (AAS)
(1)两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
(2)书写格式:如图所示,在列举两个三角形全等的条件时,如:
在△ABC和△A′B′C′中,
∠A=∠A′
∠B=∠B′
AC=A′C′
∴△ABC≌△A′B′C′(SAS).
由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.
【新知导学】
例2-1.如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠3,∠E=∠C,AE=AC,问△ABC≌△ADE吗?请说明理由.
【解析】根据三角形的外角性质得出∠ADC=∠B+∠1,求出∠ADC=∠3+∠ADE,求出∠B=∠ADE,再根据全等三角形的判定定理AAS推出全等即可.
解:△ABC和△ADE全等,
理由是:∵∠ADC=∠B+∠1=∠3+∠ADE,
又∵∠1=∠3,
∴∠B=∠ADE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(AAS),
即△ABC和△ADE全等.
【对应导练】
1.如图,点D,E在△ABC的边BC上,∠B=∠C,BD=CE,求证:△ABD≌△ACE.
【解析】根据等角对等边可得AB=AC,然后利用SAS证明△ABD≌△ACE,即可解答.
证明:∵∠B=∠C,
∴AB=AC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS).
2.如图,点B、F、C、E在同一条直线上,∠A=∠D,∠B=∠E,BF=CE,求证:△ABC≌△DEF.
【解析】首先利用等式的性质求出BC=EF,进而利用全等三角形的判定定理AAS证明两个三角形全等.
证明:∵BF=CE,
∴BF+FC=CE+FC即BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
3.已知:如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,且MS=PS.求证:△MNS≌△SQP.
【解析】首先求出∠M=∠PSQ,进而利用AAS证明△MNS≌△SQP.
解:∵MS⊥PS,MN⊥SN,PQ⊥SN,
∴∠M+∠MSN=∠MSN+∠PSQ,
∴∠M=∠PSQ;
在△MNS与△SQP中,
,
∴△MNS≌△SQP(AAS).
知识点3判定方法的选择
1.选择哪种判定方法,要根据具体的已知条件而定,见下表:
已知条件 可选择的判定方法
一边一角对应相等 SAS AAS ASA
两角对应相等 ASA AAS
两边对应相等 SAS SSS
2.如何选择三角形证全等
(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;
(2)可以从已知出发,看已知条件确定证哪两个三角形全等;
(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;
(4)如果以上方法都行不通,就添加辅助线,构造全等三角形.
注意: 三个角对应相等的两个三角形不一定全等.
【新知导学】
例3-1.如图,BC=EC,∠1=∠2,添加一个适当的条件使△ABC≌△DEC,则需添加的条件是____________(不添加任何辅助线).
【答案】∠A=∠D(答案不唯一).
【解析】先说明∠ACB=∠DCE,再添加∠A=∠D,再结合BC=EC运用AAS即可证明△ABC≌△DEC.
解:添加条件:∠A=∠D;
∵∠1=∠2,
∴∠1+∠ECA=∠2+∠ECA即∠ACB=∠DCE
在△ABC和△DEC中
∠A=∠D ,∠ACB=∠DCE,BC=EC
∴△ABC≌△DEC(AAS).
故答案为:∠A=∠D(答案不唯一).
【点睛】本题考查了全等三角形的判定定理;掌握全等三角形的判定方法是解答本题的关键.
【对应导练】
1.如图,点B,E,C,F在一条直线上,BC=EF,∠B=∠DEF.只需添加一个条件即可证明△ABC≌△DEF,这个条件可以是 _____(写出一个即可).
【答案】AB=DE或∠A=∠D或∠ACB=∠DFE
【解析】根据“SAS”或“AAS”或“ASA”添加条件.
解:∵BC=EF,∠B=∠DEF.
∴当添加AB=DE时,根据“SAS”可判断△ABC≌△DEF;
当添加∠A=∠D时,根据“AAS”可判断△ABC≌△DEF;
当添加∠ACB=∠DFE时,根据“ASA”可判断△ABC≌△DEF;
故答案为:AB=DE或∠A=∠D或∠ACB=∠DFE.
2.如图,在△ABC和△FED中,AD=FC,∠A=∠F,请添加一个条件:_____,使△ABC≌△FED.
【答案】AB=FE或∠B=∠E或∠ACB=∠FDE或DE∥BC
【解析】根据三角形的判定定理:SSS、SAS、AAS进行判断即可.
解:∵AD=FC,
∴AC=FD,
∵∠A=∠F,
∴添加AB=FE,利用SAS得出△ABC≌△FED,
添加∠B=∠E,利用AAS得出△ABC≌△FED,
添加∠ACB=∠FDE,利用ASA得出△ABC≌△FED,
添加DE∥BC,得出∠EDF=∠BCA,利用ASA得出△ABC≌△FED,
故答案为:AB=FE或∠B=∠E或∠ACB=∠FDE或DE∥BC.
3.已知:如图,在△ABC和△DEF中,B,E,C,F在同一条直线上.下面四个条件:
①AB=DE;②AC=DF;③BE=CF;④∠ABC=∠DEF.
(1)请选择其中的三个条件,使得△ABC≌△DEF(写出一种情况即可).
(2)在(1)的条件下,求证:△ABC≌△DEF.
【解析】(1)根据两三角形全等的判定定理,选择合适的条件即可.
(2)根据(1)中所选条件,进行证明即可.
解:(1)由题知,
选择的三个条件是:①②③;
或者选择的三个条件是:①③④.
证明:(2)当选择①②③时,
∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS).
当选择①③④时,
∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
二、题型训练
1.利用角边角进行证明与计算
1.如图,点A、D、B、E在同一条直线上,若AD=BE,∠A=∠EDF,∠E=∠ABC求证:AC=DF.
【答案】见解析
【分析】由知,结合,,依据“”可判定≌,依据两三角形全等对应边相等可得.
【详解】证明:,
,即,
在和中,
,
,
.
【点评】本题主要考查全等三角形的判定与性质,掌握全等三角形的判定与性质是解题的关键.
2 .如图,AC//BD,AE,BE分别平分∠CAB和∠DBA,CD经过点E.求证:CE=DE.
【答案】证明见解析
【分析】在上截取,连接,通过证明和,然后根据全等三角形的性质分析求证.
【详解】证明:在上截取,连接.
∵,分别平分和,
∴.
∵,
∴,
在和中,
∴,
∴,
∵,
∴,
在和中,
∴,
∴,
∴.
【点评】本题考查全等三角形的判定和性质,通过添加辅助线构造全等三角形是解题关键.
2.利用角角边进行证明或计算
3 .如图,AB=AC,BE⊥AC于E,CD⊥AB于D,BE、CD交于点O,求证:OB=OC.
【分析】证△ABE≌△ACD,推出∠B=∠C,AD=AE,求出BD=CE,证△BDO≌△CEO,根据全等三角形的性质推出即可.
证明:∵BE⊥AC,CD⊥AB,
∴∠ADC=∠AEB=90°,
在△ABE和△ACD中
∴△ABE≌△ACD (AAS),
∴∠B=∠C,AD=AE,
∵AB=AC,
∴BD=CE,
在△BDO和△CEO中
∴△BDO≌△CEO (AAS),
∴OB=OC.
【点拨】本题考查了全等三角形的性质和判定的应用,主要考查学生的推理能力.
4 .(1)如图1,在等腰直角 ABC中,∠ACB=90°,AC=BC,过点C作直线DE,AD⊥DE于D,BE⊥DE于,求证:;
如图2,在等腰直角 ABC中,∠ACB=90°,AC=BC,过点C作直线CE,AD⊥DE于D,BE⊥DE于E ,AD=2.5cm,DF=2.7cm,求BE的长
(3)如图3,在平面直角坐标系中,A(-1,0),C(1,3), ABC为等腰直角三角形∠ACB=90°,AC=BC,求点B坐标.
【答案】(1)证明见解析
(2)
(3)
【分析】(1)由题意知,由,,可得,进而结论得证;
(2)同理(1)证明,则,,根据计算求解的值即可;
(3)如图3,过点作平行于轴的直线,过作于,过作于,由(1)可得,则,,进而可求点坐标.
【详解】(1)证明:∵,,
∴,
∵,,
∴,
在和中,
∵,
∴;
(2)解:∵,,
∴,
∵,,
∴,
在和中,
∵,
∴,
∴,,
∴,
∴的长为;
(3)解:如图3,过点作平行于轴的直线,过作于,过作于,
由(1)可得,
∴,,
∴.
【点评】本题考查了三角形内角和定理,全等三角形的判定与性质等知识.解题的关键在于证明三角形全等.
截长补短法证明一条相等等于两条线段的和
5.已知中,,、是角平分线,他们相交于P,于P交的延长线于F,交于H.
(1)求的度数;
(2)求证:;
(3)连接,是否存在数m,使得?若存在,求出m;若不存在,说明理由.
答案:(1)
(2)证明见解析
(3)存在,
解析:(1)证明:,
,
又、分别平分、,
,
.
(2),,
又,
,
,
在和中,
,
,
,
,
,
在和中,
,
,
,
又,
.
(3)存在..
理由:连接,,
,,
,,,
,
,
,
,
,
.
6.综合与实践徐老师给爱好学习的小敏和小洁提出这样一个问题:如图1,在中,,是的平分线.
求证:.
(1)解决问题:小敏的证明思路:在上截取,连接.(如图2)
小洁的证明思路:延长至点E,使,连接.(如图3)
请你任意选择一种思路完成证明.
(2)问题升华:如图4,在中,若,,是外角的平分线,交的延长线于点D,则线段,,之间的数量关系又如何?请证明.
答案:(1)见解析
(2)
解析:(1)小敏的证明思路:如图2,在上截取,连接.
是的平分线,
,
在与中,
,
,
,,
,,
,
,
.
小洁的证明思路:如图3,延长至点E,使,连接,则,
,
.
,
,
,
是的平分线,
.
,,,
,
,
.
(2)如图在的延长线上取一点E,使,连接,
平分,
在与中,
,
,
,,
,
,
,
,
,
,
.
三、牛刀小试
一、单选题(每小题4分,共32分)
1.如图,在与中,点F在BC上,AB交EF于点D.,,,,则( )
A. B. C. D.
答案:A
解析:,.在与中,,,.,,,.
2.如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
答案:C
解析:在和中
,,
当时,满足,可证明,故选项A符合题意;
当时,满足,可证明,故选项B符合题意;
当时,满足,不能证明,故选项C不符合题意;
当时,满足,可证明,故选项D符合题意;
故选:C.
3.如图,已知,添加一个条件,使得,下列条件添加错误的是( )
A. B. C. D.
答案:B
解析:A、在和中
,
,故本选项不符合题意;
B、,,不能推,故本选项符合题意;
C、在和中
,
,故本选项不符合题意;
D、在和中
,
,故本选项不符合题意;
故选:B.
4.如图,点E在AB上,点F在上,,,与BF相交点D,连接AD,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
答案:D
解析:,,,,,,.又,,,.,,,.又,,,由上可得,图中全等三角形共有4对.
5.如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.
A. B. C. D.和
答案:C
解析:A、第块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;
B、第块,仅保留了原三角形的一部分边,所以该块不行;
C、第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合判定,符合题意;
D、由上分析,和不符合题意;
故选:C.
6.的6个元素,如图所示,下面甲、乙、丙三个三角形中和全等的是( )
A.只有乙 B.只有丙 C.甲和乙 D.乙和丙
答案:D
解析:甲的边a,c的夹角和的边a,c的夹角不对应,故甲三角形与不全等;
甲的边a,c的夹角和的边a,c的夹角对应为,故可利用“边角边”证明乙三角形与全等;
丙的角,和边a与的角和边a对应,故可利用“角角边”证明丙三角形与全等,
甲、乙、丙三个三角形中和全等的是乙和丙,
故选:D.
7.如图,在中,于点D,于点E,与交于点F,,则的长度为( )
A.10 B.6 C.5 D.4.5
答案:C
解析: ,,
,
,,,
,
在和中,
,
,
,
;
故选:C.
8.如图,点O在AD上,,,,,,则OC的长为( )
A.2 B.3 C.4 D.6
答案:C
解析:,
,
,,
,
,,
,,
.
故选:C.
二、填空题(每小题4分,共20分)
9.如图,已知,添加下列条件中的一个:①,②,③,其中不能确定的是_____(只填序号).
答案:②
解析:已知,且,
若添加①,则可由判定;
若添加②,则属于边边角的顺序,不能判定;
若添加③,则属于边角边的顺序,可以判定.
故答案为②..
10.如图,在中,点D在AB边上,E是AC边的中点,,CF与DE的延长线交于点F,若,,则BD的长为_______.
答案:1
解析:,
,,
是AC的中点,
,
在与中,
,
,
,
,
故答案为:1.
11.如图,在由6个相同的小正方形拼成的网格中,______°.
答案:180
解析:,,,
,
,
.
故答案是:180.
12.如图,已知,要用“”说明,则需添加的一个条件是_____.
答案:
解析:添加条件.
在和中,,
,
故答案为:.
13.如图,已知,E为DF的中点,若,,则________cm.
答案:6
解析:,
,,
在和中
,
,
,
.
三、解答题(共6小题,共48分)
14.(8分)如图,在中,,,于点E,且.求证:.
答案:见解析
解析:证明:,,
,
,
,
在和中,
,
.
15.(8分)如图,与交于点O,,.求证:.
答案:见解析
解析:在和中,
,
,
16.(8分)如图所示,在四边形ABCD中,,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
(1)判断FC与AD的数量关系,并说明理由;
(2)若,判断BE与AF的位置关系,并说明理由.
答案:(1),理由见解析
(2),理由见解析
解析:(1)结论:.
理由:,
,
E是CD的中点,
,
在与中,
,
,
;
(2)结论:.
理由:由(1)知,
,,
,
,
即,
,
,
.
17(8分).如图,已知,,,求证:.
答案:见解析
解析:,
.
即,
在和中,
,
.
.
18.(8分)如图,四边中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
答案:(1)见解析
(2)3
解析:(1),
,
即:,
在和中,
,
,
;
(2),
,
,,
.
19.(8分)在练习课上,慧慧同学遇到了这样一道数学题:如图,把两个全等的直角三角板的斜边重合,组成一个四边形ACBD,,以D为顶点作,交边AC,BC于点M,N,,连接MN.
探究AM,MN,BN三条线段之间的数量关系.
慧慧分析:可先利用旋转,把其中的两条线段“接起来”,再通过证明两三角形全等,从而探究出AM,MN,BN三条线段之间的数量关系.
慧慧编题:在编题演练环节,慧慧编题如下:
如图(1),把两个全等的直角三角板的斜边重合,组成一个四边形,,以D为顶点作,交边AC,BC于点M,N,,连接MN.(1)先猜想AM,MN,BN三条线段之间的数量关系,再证明.(2)绕点D旋转,当M,N分别在CA,BC的延长线上,完成图(2),其余条件不变,直接写出AM,MN,BN三条线段之间的数量关系.
请你解答:请对慧慧同学所编制的问题进行解答.
答案:(1),证明见解析
(2),证明见解析
解析:(1),
证明:延长CB到E,使,连接DE,
,,,
,
,
,
,,
,
,
,,
在和中,
,
,
,,
,,
,
,
,
,
在和中,
,
,
,
,
,
(2),
证明:在CB截取,连接DE,
,,,
,
,,
,
,
,
,
,
在和中
,
,
,,
,
,
在和中,
,
,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
