第十四章 整式的乘法与因式分解 数学活动 课件
文档属性
| 名称 | 第十四章 整式的乘法与因式分解 数学活动 课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 138.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-18 00:00:00 | ||
图片预览







文档简介
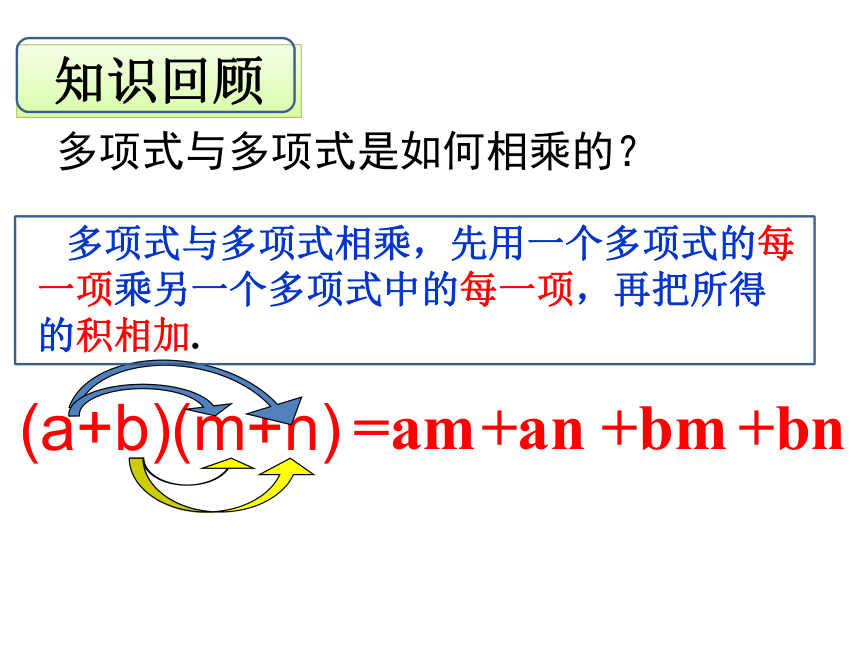
课件15张PPT。多项式与多项式是如何相乘的? (a+b)(m+n)=am+an+bm+bn 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式中的每一项,再把所得的积相加.知识回顾
计算下列多项式的积,并观察算式和结果的特征 。
(1)( x + 1 )( x – 1) = _______
(2)( m - 2 )( m + 2 ) = _______
( 3)2x + 1 )( 2x – 1 ) = ______x2-1m2- 44x2-1(x)2-12(m)2-22 (2x)2-12规律:两个数的和与这两个数的差的乘积等于相同项的平方减去相反项的平方.1(a+b)(a-b) ==a2- b2.a2- ab+ab- b2(a+b)(a-b)=a2- b2.如果用字母a、b表示等式左边,能否得出以上规律? 14.2.1 平方差公式一般地,我们有即两个数的和与这两个数的差的积,等于这两个数的平方差.这个公式叫做(乘法的)平方差公式.(a+b)(a?b)=a2?b2平方差概念:
(a+b)(a-b)=(a)2-(b)2这个公式我们要注意两点:
1.左边要有两个括号相乘,两个括号中分别有两项相同,另两项相反.(平方差公式的运用条件)2.右边结果是相同项整体的平方减去相反项整体的平方.(公式的正确运用)(不能) (能) (能) (不能) 11/23/2018 口答下列各题:
(l)(-a+b)(a+b)=??_________
(2)(a-b)(b+a)= __________
(3)(-a-b)(-a+b)= ________
(4)(a-b)(-a-b)= _________a2-b2a2-b2b2-a2b2-a2例1:运用平方差公式计算。
⑴(3x+2)(3x-2) ⑵(2a+5b2)(2a-5b2)解 ⑴(3x+2)(3x-2)= ↓ ↓ ↓ ↓
(a + b)(a - b)= a2 - b2(3x)2-22 ⑵ (2a+5b2)(2a-5b2) ↑ ↑ =9x2-4 ↓ ↓ ↓ ↓ ↑ ↑
( a +b )( a- b) = a2 - b2=(2a)2-(5b2)2 =4a2-25b4 .运用平方差公式进行计算
(1) (b+2a)(2a-b)
(2) (-x+2y)(-x-2y)
(3) (ab +4)(ab-4)
练习11/23/2018例2 计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .解: (1) 102×98(y+2)(y-2)- (y-1)(y+5)= 1002-22=10000 – 4 =(100+2)(100-2)=9996= y2-22-(y2+4y-5)= y2-4-y2-4y+5= - 4y + 1.挑战自我11/23/20181、利用平方差公式计算:(a-2)(a+2)(a2 + 4)
解:原式=(a2-4)(a2+4)
=a4-16
拓展提升11/23/2018知难而进2.计算 20042 - 2003×2005;解:
20042 - 2003×2005= 20042 - (2004-1)(2004+1)= 20042- (20042-12 )= 20042- 20042+12 =1课堂小结:1.平方差公式:(a+b)(a-b) = a - b2.平方差公式的运用条件及正确运用.22课后作业:
练习1、2
计算下列多项式的积,并观察算式和结果的特征 。
(1)( x + 1 )( x – 1) = _______
(2)( m - 2 )( m + 2 ) = _______
( 3)2x + 1 )( 2x – 1 ) = ______x2-1m2- 44x2-1(x)2-12(m)2-22 (2x)2-12规律:两个数的和与这两个数的差的乘积等于相同项的平方减去相反项的平方.1(a+b)(a-b) ==a2- b2.a2- ab+ab- b2(a+b)(a-b)=a2- b2.如果用字母a、b表示等式左边,能否得出以上规律? 14.2.1 平方差公式一般地,我们有即两个数的和与这两个数的差的积,等于这两个数的平方差.这个公式叫做(乘法的)平方差公式.(a+b)(a?b)=a2?b2平方差概念:
(a+b)(a-b)=(a)2-(b)2这个公式我们要注意两点:
1.左边要有两个括号相乘,两个括号中分别有两项相同,另两项相反.(平方差公式的运用条件)2.右边结果是相同项整体的平方减去相反项整体的平方.(公式的正确运用)(不能) (能) (能) (不能) 11/23/2018 口答下列各题:
(l)(-a+b)(a+b)=??_________
(2)(a-b)(b+a)= __________
(3)(-a-b)(-a+b)= ________
(4)(a-b)(-a-b)= _________a2-b2a2-b2b2-a2b2-a2例1:运用平方差公式计算。
⑴(3x+2)(3x-2) ⑵(2a+5b2)(2a-5b2)解 ⑴(3x+2)(3x-2)= ↓ ↓ ↓ ↓
(a + b)(a - b)= a2 - b2(3x)2-22 ⑵ (2a+5b2)(2a-5b2) ↑ ↑ =9x2-4 ↓ ↓ ↓ ↓ ↑ ↑
( a +b )( a- b) = a2 - b2=(2a)2-(5b2)2 =4a2-25b4 .运用平方差公式进行计算
(1) (b+2a)(2a-b)
(2) (-x+2y)(-x-2y)
(3) (ab +4)(ab-4)
练习11/23/2018例2 计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .解: (1) 102×98(y+2)(y-2)- (y-1)(y+5)= 1002-22=10000 – 4 =(100+2)(100-2)=9996= y2-22-(y2+4y-5)= y2-4-y2-4y+5= - 4y + 1.挑战自我11/23/20181、利用平方差公式计算:(a-2)(a+2)(a2 + 4)
解:原式=(a2-4)(a2+4)
=a4-16
拓展提升11/23/2018知难而进2.计算 20042 - 2003×2005;解:
20042 - 2003×2005= 20042 - (2004-1)(2004+1)= 20042- (20042-12 )= 20042- 20042+12 =1课堂小结:1.平方差公式:(a+b)(a-b) = a - b2.平方差公式的运用条件及正确运用.22课后作业:
练习1、2
