人教版八年级数学上名师点拨精练第12章全等三角形12.2 三角形全等的判定微专题全等三角形应用的常见类型(含解析)
文档属性
| 名称 | 人教版八年级数学上名师点拨精练第12章全等三角形12.2 三角形全等的判定微专题全等三角形应用的常见类型(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-07 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.2 三角形全等的判定
微专题 全等三角形应用的常见类型
老师告诉你
全等三角形的对应边相等、对应角相等,为我们提供了解决线段相等,角相等的新思路、新方法,因此,判定两个三角形全等是解决线段相等,角相等的问题的基础,全等三角形的判定和性质的应用是各类考试的必考内容之一,主要题型有证明线段、角相等关系、和差关系、位置关系等.
类型一、全等三角形在证明线段相等角相等中的应用
【典例剖析】
例1-1.如图,在△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,点F在BC上,连接DF,且AD=DF.
(Ⅰ)求证:CF=AE;
(Ⅱ)若AE=3,BF=4,求AB的长.
例1-2.如图,点B在线段AC上,BD∥CE,AB=EC,DB=BC.求证:AD=EB.
【针对训练】
1.已知:如图,AB∥DE,AB=DE,AF=DC.求证:∠B=∠E.
2.如图,在中,,、分别为、上一点,.若,求证:.
3.如图,CA=CD,CB=CE,AB=DE,AB与DE交于点M.
(1)求证:∠ACD=∠BCE;
(2)连MC,若∠BMC=78°,求∠BMD的度数.
类型二、全等三角形在证明线段和差关系的应用
【典例剖析】
例2-1.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
例2-2.综合与实践:
数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
(1)发现问题:如图1,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=30°,连接BE,CF,延长BE交CF于点D.则BE与CF的数量关系:_____,∠BDC=_____°;
(2)类比探究:如图2,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=120°,连接BE,CF,延长BE,FC交于点D.请猜想BE与CF的数量关系及∠BDC的度数,并说明理由;
(3)拓展延伸:如图3,△ABC和△AEF均为等腰直角三角形,∠BAC=∠EAF=90°,连接BE,CF,且点B,E,F在一条直线上,过点A作AM⊥BF,垂足为点M.则BF,CF,AM之间的数量关系:_____;
【针对训练】
1.已知:四边形中,,,,对角线相交于点O,且平分,过点A作,垂足为H.判断线段之间的数量关系:___________;并证明你的结论.
2.如图1,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE.连结BE,CD,作AF⊥CD,垂足为F,交BE于点G.
(1)若∠GAE=70°,求∠ADC的度数;
(2)如图2,作EH⊥GF,垂足为H,HF=7,求EH+DF的长;
(3)求证:BG=EG.
3.如图,AD是△ABC的中线,BE⊥AD,垂足为E,CF⊥AD,交AD的延长线于点F,G是DA延长线上一点,连接BG.
(1)求证:BE=CF;
(2)若BG=CA,求证:GA=2DE.
类型三、全等三角形在证明线段位置关系的应用
【典例剖析】
例3-1.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
例3-2.已知AB=CD,AD=BC.求证:
①AD∥BC;
②∠B=∠D.
【针对训练】
1.两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:DC⊥BE.
2.如图,,,,在同一条直线上,于点,于点,,,求证:.
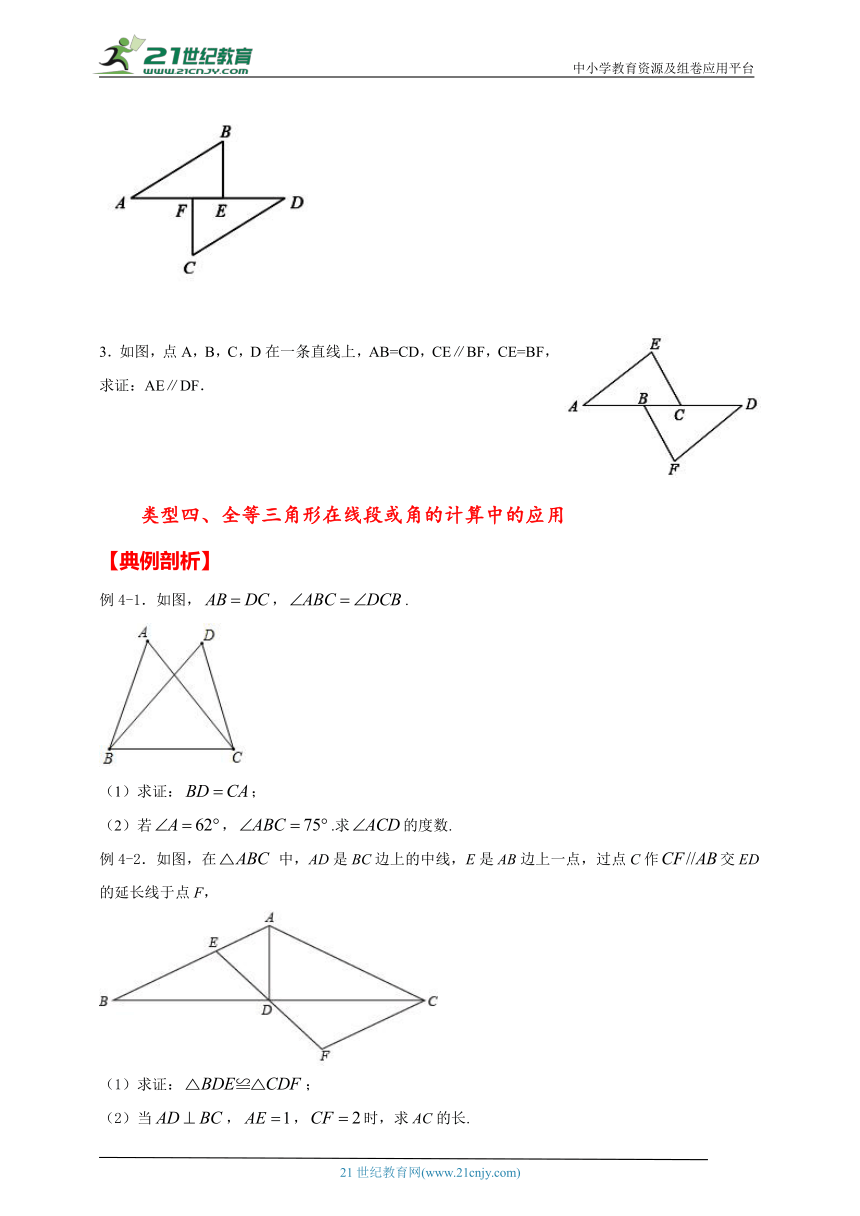
3.如图,点A,B,C,D在一条直线上,AB=CD,CE∥BF,CE=BF,求证:AE∥DF.
类型四、全等三角形在线段或角的计算中的应用
【典例剖析】
例4-1.如图,,.
(1)求证:;
(2)若,.求的度数.
例4-2.如图,在中,AD是BC边上的中线,E是AB边上一点,过点C作交ED的延长线于点F,
(1)求证:;
(2)当,,时,求AC的长.
【针对训练】
1.如图.点A,B,C,D在同一条直线上,点E,F分别在直线的两侧,且,,.
(1)求证:;
(2)若,,求的长.
2.如图,四边中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
3.如图,以的两边AC,BC为边分别向外作和,使得,,.
(1)求证:;
(2)若,,求的度数.
4.如图,C是线段AB的中点,CD平分,CE平分,.
(1)求证:;
(2)若,求的度数.
类型五、全等三角形在生活实际中的应用
【典例剖析】
例5-1.小明在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆点O处用一根细绳悬挂一个小球A,小球A可以自由摆动,如图,OA表示小球静止时的位置.当小明用发声物体靠近小球时,小球从OA摆到OB位置,此时过点B作BD⊥OA于点D,当小球摆到OC位置时,OB与OC恰好垂直(图中的A、B、O、C在同一平面上),过点C作CE⊥OA于点E,测得CE=15cm,OE=8cm.
(1)试说明:OE=BD;
(2)求DE的长.
例5-2.如图,小明在游乐场玩两层型滑梯,每层楼梯的高度相同(EH=HD),都为2.5米,他想知道左右两个滑梯BC和EF的长度是否相等,于是制定了如下方案:
课题 探究两个滑梯的长度是否相等
测量工具 长度为6米的米尺
测量步骤 ①测量出线段FD的长度
②测量出线段AB的长度
测量数据 DF=2.5米,AB=5米
(1)根据小明的测量方案和数据,判断两个滑梯BC和EF的长度是否相等?并说明理由.
(2)试猜想左右两个滑梯BC和EF所在直线的位置关系,并加以证明.
【针对训练】
1.如图,小明站在堤岸凉亭A点处,正对他的S点停有一艘游艇,他想知道凉亭与这艘游艇之间的距离,于是制定了如下方案.
课题 测凉亭与游艇之间的距离
测量工具 皮尺等
测量方案示意图
测量步骤 ①小明沿堤岸走到电线杆B旁;
②再往前走相同的距离,到达C点;
③然后他向左直行,当看到电线杆与游艇在一条直线上时停下来.
测量数据 AB=10米,BC=10米,CD=5米
(1)凉亭与游艇之间的距离是 _____米.
(2)请你说明小明做法的正确性.
2.如图,这是王玲家的养鱼塘,王玲想要测量鱼塘的宽AB,请你帮助她设计一个不必下水而且简单可行的方案,并说明理由,要求在原图上画出该方案的示意图.
3.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.2 三角形全等的判定
微专题 全等三角形应用的常见类型(解析版)
老师告诉你
全等三角形的对应边相等、对应角相等,为我们提供了解决线段相等,角相等的新思路、新方法,因此,判定两个三角形全等是解决线段相等,角相等的问题的基础,全等三角形的判定和性质的应用是各类考试的必考内容之一,主要题型有证明线段、角相等关系、和差关系、位置关系等.
类型一、全等三角形在证明线段相等角相等中的应用
【典例剖析】
例1-1.如图,在△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,点F在BC上,连接DF,且AD=DF.
(Ⅰ)求证:CF=AE;
(Ⅱ)若AE=3,BF=4,求AB的长.
【解析】(Ⅰ)通过HL证明Rt△CDF≌Rt△EDA,即可得出结论;
(Ⅱ)通过HL证明△BED≌△BCD,得BE=BC,再进行等量代换即可.
证明:(Ⅰ)∵∠C=90°,AD是∠BAC的平分线,DE⊥AB,
∴DE=DC,∠AED=90°,
在Rt△CDF与Rt△EDA中,
,
∴Rt△CDF≌Rt△EDA(HL),
∴CF=AE;
(Ⅱ)∵CF=AE,AE=3,
∴CF=3,
∵BF=4,
∴BC=BF+CF=4+3=7,
∵DE⊥AB,
∴∠DEB=90°,
∵∠C=90°,
∴∠DEB=∠C,
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD,
在△BED和△BCD中,
,
∴△BED≌△BCD(AAS),
∴BE=BC=7,
∴AB=BE+AE=7+3=10.
例1-2.如图,点B在线段AC上,BD∥CE,AB=EC,DB=BC.求证:AD=EB.
【解析】由平行线的性质可得∠A=∠EBC,由“AAS”可证△ABD≌△BEC,可得BD=EC.
证明:∵BD∥CE,
∴∠ABD=∠C,
在△ABD和△ECB中,
∴△ABD≌△ECB(SAS),
∴AD=EB.
【针对训练】
1.已知:如图,AB∥DE,AB=DE,AF=DC.求证:∠B=∠E.
【解析】由AF=DC,得AC=DF,由AB∥DE,得∠A=∠D,即可证△ABC≌△DEF(SAS),故∠B=∠E.
证明:∵AF=DC,
∴AF+CF=DC+CF,即AC=DF,
∵AB∥DE,
∴∠A=∠D,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠B=∠E.
2.如图,在中,,、分别为、上一点,.若,求证:.
【答案】见解析
【解析】先根据条件得出,,再根据判定,即可得到.
解:证明:,
,
,
,
,,
,
在与中,
,
,
.
【点睛】本题主要考查了全等三角形的判定与性质、等腰三角形的性质等知识;熟练掌握等腰三角形的性质,证明三角形全等是解题的关键.
3.如图,CA=CD,CB=CE,AB=DE,AB与DE交于点M.
(1)求证:∠ACD=∠BCE;
(2)连MC,若∠BMC=78°,求∠BMD的度数.
【解析】(1)根据SSS证明△ABC≌△DEC,进而利用全等三角形的性质解答即可;
(2)根据AAS证明△AGC≌△DHC,进而利用全等三角形的性质解答即可.
证明:(1)在△ABC和△DEC中,
,
∴△ABC≌△DEC(SSS),
∴∠ACB=∠DCE,
∴∠ACD=∠BCE;
(2)过C作CG⊥AB于G,CH⊥DE于H,
∵△ABC≌△DEC,
∴∠A=∠D,AC=DC,
∵∠AGC=∠DHC=90°,
在△AGC和△DHC中,
,
∴△AGC≌△DHC(AAS),
∴CG=CH,
∴MC平分∠BMD,
∴∠BMD=2∠BMC=2×78°=156°.
类型二、全等三角形在证明线段和差关系的应用
【典例剖析】
例2-1.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
【解析】(1)①由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,推出∠DAC=∠BCE,根据AAS即可得到答案;
②由(1)得到AD=CE,CD=BE,即可求出答案;
(2)与(1)证法类似可证出∠ACD=∠EBC,能推出△ADC≌△CEB,得到AD=CE,CD=BE,代入已知即可得到答案.
(1)①证明:∵AD⊥DE,BE⊥DE,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中
,
∴△ADC≌△CEB(AAS).
②证明:由(1)知:△ADC≌△CEB,
∴AD=CE,CD=BE,
∵DC+CE=DE,
∴AD+BE=DE.
(2)证明:∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中
,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=EC-CD=AD-BE.
例2-2.综合与实践:
数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
(1)发现问题:如图1,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=30°,连接BE,CF,延长BE交CF于点D.则BE与CF的数量关系:_____,∠BDC=_____°;
(2)类比探究:如图2,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=120°,连接BE,CF,延长BE,FC交于点D.请猜想BE与CF的数量关系及∠BDC的度数,并说明理由;
(3)拓展延伸:如图3,△ABC和△AEF均为等腰直角三角形,∠BAC=∠EAF=90°,连接BE,CF,且点B,E,F在一条直线上,过点A作AM⊥BF,垂足为点M.则BF,CF,AM之间的数量关系:_____;
【答案】(1)BE=CF;(2)30;(3)BF=CF+2AM;
【解析】(1)根据等腰三角形的性质,利用SAS证明△ABE≌△ACF即可得出结论;
(2)根据等腰三角形的性质,利用SAS证明△BAE≌△CAF即可得出结论;
(3)根据等腰直角三角形的性质,利用SAS证明△BAE≌△CAE即可得出结论;
(4)根据直径所对的圆周角是直角,先找到点P,利用勾股定理计算出BP,再利用第3小题的结论得到三角形的高,△ABP的面积即可求出.
解:(1)BE=CF,∠BDC=30°,
理由如下:如图1所示:
∵△ABC和△ADE都是等腰三角形,
∴AB=AC,AE=AF,
又∵∠BAC=∠EAF=30°,
∴△ABE≌△ACF(SAS),
∴BE=CF,
∴∠ABE=∠ACD,
∵∠AOE∠ABE+∠BAC,
∠AOE=∠ACD+∠BDC,
∴∠BDC=∠BAC=30°;
(2)BE=CF,∠BDC=60°,
理由如下:如图2所示:
证明:∵∠BAC=∠EAF=120°,
∴∠BAC-∠EAC=∠EAF-∠EAC,
即∠BAE=∠CAF,
又∵△ABC和△AEF都是等腰三角形,
∴AB=AC,AE=AF,
∴△BAE≌△CAF(SAS)
∴BE=CF,
∴∠AEB=∠AFC,
∵∠EAF=120°,AE=AF,
∴∠AEF=∠AFE=30°,
∴∠BDC=∠BEF-∠EFD=∠AEB+30°-(∠AFC-30°)=60°;
(3)BF=CF+2AM,
理由如下:如图3所示:
∵△ABC和△AEF都是等腰三角形,
∴∠CAB=∠EAF=90°,AB=AC,AE=AF,
∴∠CAB-∠CAE=∠FAE-∠CAE,
即:∠BAE=∠CAF,
∴△BAE≌△CAE(SAS),
∴BE=CF,
∵AM⊥BF,AE=AF,EAF=90°,
∴EF=2AM,
∵BF=BE+EF,
∴BF=CF+2AM;
【针对训练】
1.已知:四边形中,,,,对角线相交于点O,且平分,过点A作,垂足为H.判断线段之间的数量关系:___________;并证明你的结论.
【答案】,证明见解析
【解析】先证明是等边三角形,再证明,最后根据三角形内角和定理证明,在上截取,先证明,得出,再证明,得出,即可解决问题.
,
证明:∵,,
∴是等边三角形,
∴,
∵,平分,
∴,
∴,
∵,,,
∴,
在上截取,
∵,
∴,
又,
∴,
∴,
∴
∵,
∴,
∴,
∵,
∴.
【点睛】此题主要考查了全等三角形的判定和性质、等边三角形的判定和性质,三角形内角和定理,角平分线的定义等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
2.如图1,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE.连结BE,CD,作AF⊥CD,垂足为F,交BE于点G.
(1)若∠GAE=70°,求∠ADC的度数;
(2)如图2,作EH⊥GF,垂足为H,HF=7,求EH+DF的长;
(3)求证:BG=EG.
【解析】(1)由∠ADC+∠DAF=90°,∠GAE+∠DAF=90°,得∠ADC=∠GAE=70°;
(2)可证明△EAH≌△ADF,EH=AF,AH=DF,则EH+DF=AF+AH=HF=7;
(3)作EH⊥FG于点H,BI⊥FG交FG的延长线于点I,可证明△BAI≌△ACF,得BI=AF,而EH=AF,所以BI=EH,可证明△BGI≌△EGH,则BG=EG.
(1)解:如图1,∵AF⊥CD,
∴∠AFD=90°,
∴∠ADC+∠DAF=90°,
∵∠DAE=90°,
∴∠GAE+∠DAF=90°,
∴∠ADC=∠GAE=70°,
∴∠ADC的度数是70°.
(2)解:如图2,∵EH⊥GF,
∴∠EHA=∠AFD=90°,
由(1)得∠EAH=∠ADF,
在△EAH和△ADF中,
,
∴△EAH≌△ADF(AAS),
∴EH=AF,AH=DF,
∴EH+DF=AF+AH=HF=7,
∴EH+DF的长是7.
(3)证明:如图3,作EH⊥FG于点H,BI⊥FG交FG的延长线于点I,
∴∠I=∠EHG=∠AFC=90°,
∵∠BAC=90°,
∴∠BAI=∠ACF=90°-∠CAF,
在△BAI和△ACF中,
,
∴△BAI≌△ACF(AAS),
∴BI=AF,
由(2)得EH=AF,
∴BI=EH,
在△BGI和△EGH中,
,
∴△BGI≌△EGH(AAS),
∴BG=EG.
3.如图,AD是△ABC的中线,BE⊥AD,垂足为E,CF⊥AD,交AD的延长线于点F,G是DA延长线上一点,连接BG.
(1)求证:BE=CF;
(2)若BG=CA,求证:GA=2DE.
【解析】(1)利用AAS证明△BED≌△CFD,得BE=CF;
(2)利用HL证明Rt△BGE≌Rt△CAF,得GE=AF,从而解决问题.
证明:(1)∵AD是△ABC的中线,
∴BD=CD,
∵BE⊥AD,CF⊥AD,
∴∠BED=∠F,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),
∴BE=CF;
(2)在Rt△BGE和Rt△CAF中,
,
∴Rt△BGE≌Rt△CAF(HL),
∴GE=AF,
∴AG=EF.
∵△BED≌△CFD,
∴DE=DF,
∴GA=2DE.
类型三、全等三角形在证明线段位置关系的应用
【典例剖析】
例3-1.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
【解析】(1)根据平行线性质求出∠A=∠B,根据SAS推出即可.
(2)根据全等三角形性质推出CD=CE,根据等腰三角形性质求出即可.
证明:(1)∵AD∥BE,
∴∠A=∠B,
在△ACD和△BEC中
∴△ACD≌△BEC(SAS),
(2)∵△ACD≌△BEC,
∴CD=CE,
又∵CF平分∠DCE,
∴CF⊥DE.
例3-2.已知AB=CD,AD=BC.求证:
①AD∥BC;
②∠B=∠D.
【解析】①连接AC,由AB=CD,BC=DA,AC=CA,根据全等三角形的判定定理“SSS”证明△ABC≌△CDA,得∠ACB=∠CAD,则AD∥BC;
②由△ABC≌△CDA,得∠B=∠D.
证明:①连接AC,
在△ABC和△CDA中,
,
∴△ABC≌△CDA(SSS),
∴∠ACB=∠CAD,
∴AD∥BC.
②△ABC≌△CDA,
∴∠B=∠D.
【针对训练】
1.两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:DC⊥BE.
【解析】(1)根据等腰直角三角形的性质,可以得出△ABE≌△ACD;
(2)由△ABE≌△ACD可以得出∠B=∠ACD-45°,进而得出∠DCB=90°,就可以得出结论.
(1)△ABE≌△ACD.
证明:∵△ABC与△AED均为等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°.
∴∠BAC+∠CAE=∠EAD+∠CAE.
即∠BAE=∠CAD,
在△ABE与△ACD中,
,
∴△ABE≌△ACD;
(2)证明∵△ABE≌△ACD,
∴∠ACD=∠ABE=45°,
又∵∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=90°,
∴DC⊥BE.
2.如图,,,,在同一条直线上,于点,于点,,,求证:.
【答案】见解析
【解析】先证明,利用全等三角形的性质解题即可.
证明:∵,
∴,
又∵
∴
在和中,
,
∴
∴
∴
【点睛】本题考查全等三角形的判定和性质,平行线的判定,掌握全等三角形的判定方法是解题的关键.
3.如图,点A,B,C,D在一条直线上,AB=CD,CE∥BF,CE=BF,求证:AE∥DF.
【解析】根据平行线的性质得出∠ACE=∠DBF,求出AC=BD,根据全等三角形的判定得出△AEC≌△DFB,根据全等三角形的性质得出∠A=∠D,根据平行线的判定得出即可.
证明:∵CE∥BF,
∴∠ACE=∠DBF,
∵AB=CD,
∴AB+BC=CD+BC,
即AC=BD,
在△AEC和△DFB中,
,
∴△AEC≌△DFB(SAS),
∴∠A=∠D,
∴AE∥DF.
类型四、全等三角形在线段或角的计算中的应用
【典例剖析】
例4-1.如图,,.
(1)求证:;
(2)若,.求的度数.
答案:(1)见详解
(2)
解析:(1)证明:在与中,
,
,
;
(2),
,
,.
,
.
例4-2.如图,在中,AD是BC边上的中线,E是AB边上一点,过点C作交ED的延长线于点F,
(1)求证:;
(2)当,,时,求AC的长.
(1)答案:见解析
解析:,
,,
是边上的中线,
,
;
(2)答案:3
解析:,
,
,
,,
.
【针对训练】
1.如图.点A,B,C,D在同一条直线上,点E,F分别在直线的两侧,且,,.
(1)求证:;
(2)若,,求的长.
答案:(1)见解析
(2)4
解析:(1)在和中,
,
;
(2),,
,
又,
.
2.如图,四边中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
答案:(1)见解析
(2)3
解析:(1),
,
即:,
在和中,
,
,
;
(2),
,
,,
.
3.如图,以的两边AC,BC为边分别向外作和,使得,,.
(1)求证:;
(2)若,,求的度数.
答案:(1)见解析
(2)
解析:(1)证明:,
,
即.
又,,
;
(2)由(1)得,
,,
.
,
,
.
4.如图,C是线段AB的中点,CD平分,CE平分,.
(1)求证:;
(2)若,求的度数.
答案:(1)证明见解析;
(2).
解析:(1)点C是线段AB的中点,
,
又平分,CE平分,
,,
在和中,
(2)
.
类型五、全等三角形在生活实际中的应用
【典例剖析】
例5-1.小明在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆点O处用一根细绳悬挂一个小球A,小球A可以自由摆动,如图,OA表示小球静止时的位置.当小明用发声物体靠近小球时,小球从OA摆到OB位置,此时过点B作BD⊥OA于点D,当小球摆到OC位置时,OB与OC恰好垂直(图中的A、B、O、C在同一平面上),过点C作CE⊥OA于点E,测得CE=15cm,OE=8cm.
(1)试说明:OE=BD;
(2)求DE的长.
【解析】(1)利用AAS证明△COE≌△OBD,可得结论;
(2)利用全等三角形性质可得答案.
解:(1)∵OB⊥OC,
∴∠BOD+∠COE=90°,
∵CE⊥OA,BD⊥OA,
∴∠CEO=∠ODB=90°,
∴∠BOD+∠B=90°,
∴∠COE=∠B,
∵OC=BO,
∴△COE≌△OBD(AAS),
∴OE=BD;
(2)∵△COE≌△OBD,
∴CE=OD=15cm,
∴DE=OD-OE=7cm.
例5-2.如图,小明在游乐场玩两层型滑梯,每层楼梯的高度相同(EH=HD),都为2.5米,他想知道左右两个滑梯BC和EF的长度是否相等,于是制定了如下方案:
课题 探究两个滑梯的长度是否相等
测量工具 长度为6米的米尺
测量步骤 ①测量出线段FD的长度
②测量出线段AB的长度
测量数据 DF=2.5米,AB=5米
(1)根据小明的测量方案和数据,判断两个滑梯BC和EF的长度是否相等?并说明理由.
(2)试猜想左右两个滑梯BC和EF所在直线的位置关系,并加以证明.
【解析】(1)证明△BAC≌△EDF(SAS),由全等三角形的性质得出BC=EF;
(2)延长BC交EF于点M,由全等三角形的性质得出∠BMF=90°,则可得出结论.
解:(1)BC=EF.
理由:∵EH=DH=2.5米,
∴ED=5米,
∴AB=DE,
由题意可知四边形CADH为矩形,
∴CA=DH=2.5米,
∵DF=2.5米,
∴CA=DF,
∵∠BAC=∠EDF=90°,
∴△BAC≌△EDF(SAS),
∴BC=EF;
(2)BC⊥EF.
理由:延长BC交EF于点M,
∵∠EDF=90°,
∴∠F+∠EDF=90°,
∵△BAC≌△EDF,
∴∠B=∠DEF,
∴∠B+∠F=90°,
∴∠BMF=90°,
∴EF⊥BM.
【针对训练】
1.如图,小明站在堤岸凉亭A点处,正对他的S点停有一艘游艇,他想知道凉亭与这艘游艇之间的距离,于是制定了如下方案.
课题 测凉亭与游艇之间的距离
测量工具 皮尺等
测量方案示意图
测量步骤 ①小明沿堤岸走到电线杆B旁;
②再往前走相同的距离,到达C点;
③然后他向左直行,当看到电线杆与游艇在一条直线上时停下来.
测量数据 AB=10米,BC=10米,CD=5米
(1)凉亭与游艇之间的距离是 _____米.
(2)请你说明小明做法的正确性.
【答案】5
【解析】根据全等三角形的判定和性质即可得到结论.
解:(1)凉亭与游艇之间的距离是5米;
故答案为:5.
(2)理由:在△ABS与△CBD中,
,
∴△ABS≌△CBD(ASA),
∴AS=CD=5米.
2.如图,这是王玲家的养鱼塘,王玲想要测量鱼塘的宽AB,请你帮助她设计一个不必下水而且简单可行的方案,并说明理由,要求在原图上画出该方案的示意图.
【解析】方案设计为:从A点出发沿与AB垂直的方向到C点,再沿AC方向走到D点,使CD=AC,接着从B点出发,沿与AD垂直的方向走到E点,使E、C、B共线,则测出DE的长解能得到AB的宽;然后根据全等三角形的判断方法证明△ACB≌△DCE,从而得到AB=DE.
解:方案设计为:
从A点出发沿与AB垂直的方向到C点,再沿AC方向走到D点,使CD=AC,接着从B点出发,沿与AD垂直的方向走到E点,使E、C、B共线,则测出DE的长解能得到AB的宽.
理由如下:∵AD⊥AB,BE⊥AD,
∴∠BAC=∠EDC,
∵∠BCA=∠ECD,AC=DC,
∴△ACB≌△DCE(ASA),
∴AB=DE.
3.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
【解析】∠BAD与∠CAD相等,证角相等,常常通过把角放到两个全等三角形中来证,本题OA=OA公共边,可考虑SSS证明三角形全等,从而推出角相等.
解:雨伞开闭过程中二者关系始终是:∠BAD=∠CAD,
理由如下:
∵AB=AC,AE=AB,AF=AC,
∴AE=AF,
在△AOE与△AOF中,
,
∴△AOE≌△AOF(SSS),
∴∠BAD=∠CAD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.2 三角形全等的判定
微专题 全等三角形应用的常见类型
老师告诉你
全等三角形的对应边相等、对应角相等,为我们提供了解决线段相等,角相等的新思路、新方法,因此,判定两个三角形全等是解决线段相等,角相等的问题的基础,全等三角形的判定和性质的应用是各类考试的必考内容之一,主要题型有证明线段、角相等关系、和差关系、位置关系等.
类型一、全等三角形在证明线段相等角相等中的应用
【典例剖析】
例1-1.如图,在△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,点F在BC上,连接DF,且AD=DF.
(Ⅰ)求证:CF=AE;
(Ⅱ)若AE=3,BF=4,求AB的长.
例1-2.如图,点B在线段AC上,BD∥CE,AB=EC,DB=BC.求证:AD=EB.
【针对训练】
1.已知:如图,AB∥DE,AB=DE,AF=DC.求证:∠B=∠E.
2.如图,在中,,、分别为、上一点,.若,求证:.
3.如图,CA=CD,CB=CE,AB=DE,AB与DE交于点M.
(1)求证:∠ACD=∠BCE;
(2)连MC,若∠BMC=78°,求∠BMD的度数.
类型二、全等三角形在证明线段和差关系的应用
【典例剖析】
例2-1.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
例2-2.综合与实践:
数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
(1)发现问题:如图1,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=30°,连接BE,CF,延长BE交CF于点D.则BE与CF的数量关系:_____,∠BDC=_____°;
(2)类比探究:如图2,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=120°,连接BE,CF,延长BE,FC交于点D.请猜想BE与CF的数量关系及∠BDC的度数,并说明理由;
(3)拓展延伸:如图3,△ABC和△AEF均为等腰直角三角形,∠BAC=∠EAF=90°,连接BE,CF,且点B,E,F在一条直线上,过点A作AM⊥BF,垂足为点M.则BF,CF,AM之间的数量关系:_____;
【针对训练】
1.已知:四边形中,,,,对角线相交于点O,且平分,过点A作,垂足为H.判断线段之间的数量关系:___________;并证明你的结论.
2.如图1,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE.连结BE,CD,作AF⊥CD,垂足为F,交BE于点G.
(1)若∠GAE=70°,求∠ADC的度数;
(2)如图2,作EH⊥GF,垂足为H,HF=7,求EH+DF的长;
(3)求证:BG=EG.
3.如图,AD是△ABC的中线,BE⊥AD,垂足为E,CF⊥AD,交AD的延长线于点F,G是DA延长线上一点,连接BG.
(1)求证:BE=CF;
(2)若BG=CA,求证:GA=2DE.
类型三、全等三角形在证明线段位置关系的应用
【典例剖析】
例3-1.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
例3-2.已知AB=CD,AD=BC.求证:
①AD∥BC;
②∠B=∠D.
【针对训练】
1.两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:DC⊥BE.
2.如图,,,,在同一条直线上,于点,于点,,,求证:.
3.如图,点A,B,C,D在一条直线上,AB=CD,CE∥BF,CE=BF,求证:AE∥DF.
类型四、全等三角形在线段或角的计算中的应用
【典例剖析】
例4-1.如图,,.
(1)求证:;
(2)若,.求的度数.
例4-2.如图,在中,AD是BC边上的中线,E是AB边上一点,过点C作交ED的延长线于点F,
(1)求证:;
(2)当,,时,求AC的长.
【针对训练】
1.如图.点A,B,C,D在同一条直线上,点E,F分别在直线的两侧,且,,.
(1)求证:;
(2)若,,求的长.
2.如图,四边中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
3.如图,以的两边AC,BC为边分别向外作和,使得,,.
(1)求证:;
(2)若,,求的度数.
4.如图,C是线段AB的中点,CD平分,CE平分,.
(1)求证:;
(2)若,求的度数.
类型五、全等三角形在生活实际中的应用
【典例剖析】
例5-1.小明在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆点O处用一根细绳悬挂一个小球A,小球A可以自由摆动,如图,OA表示小球静止时的位置.当小明用发声物体靠近小球时,小球从OA摆到OB位置,此时过点B作BD⊥OA于点D,当小球摆到OC位置时,OB与OC恰好垂直(图中的A、B、O、C在同一平面上),过点C作CE⊥OA于点E,测得CE=15cm,OE=8cm.
(1)试说明:OE=BD;
(2)求DE的长.
例5-2.如图,小明在游乐场玩两层型滑梯,每层楼梯的高度相同(EH=HD),都为2.5米,他想知道左右两个滑梯BC和EF的长度是否相等,于是制定了如下方案:
课题 探究两个滑梯的长度是否相等
测量工具 长度为6米的米尺
测量步骤 ①测量出线段FD的长度
②测量出线段AB的长度
测量数据 DF=2.5米,AB=5米
(1)根据小明的测量方案和数据,判断两个滑梯BC和EF的长度是否相等?并说明理由.
(2)试猜想左右两个滑梯BC和EF所在直线的位置关系,并加以证明.
【针对训练】
1.如图,小明站在堤岸凉亭A点处,正对他的S点停有一艘游艇,他想知道凉亭与这艘游艇之间的距离,于是制定了如下方案.
课题 测凉亭与游艇之间的距离
测量工具 皮尺等
测量方案示意图
测量步骤 ①小明沿堤岸走到电线杆B旁;
②再往前走相同的距离,到达C点;
③然后他向左直行,当看到电线杆与游艇在一条直线上时停下来.
测量数据 AB=10米,BC=10米,CD=5米
(1)凉亭与游艇之间的距离是 _____米.
(2)请你说明小明做法的正确性.
2.如图,这是王玲家的养鱼塘,王玲想要测量鱼塘的宽AB,请你帮助她设计一个不必下水而且简单可行的方案,并说明理由,要求在原图上画出该方案的示意图.
3.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.2 三角形全等的判定
微专题 全等三角形应用的常见类型(解析版)
老师告诉你
全等三角形的对应边相等、对应角相等,为我们提供了解决线段相等,角相等的新思路、新方法,因此,判定两个三角形全等是解决线段相等,角相等的问题的基础,全等三角形的判定和性质的应用是各类考试的必考内容之一,主要题型有证明线段、角相等关系、和差关系、位置关系等.
类型一、全等三角形在证明线段相等角相等中的应用
【典例剖析】
例1-1.如图,在△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,点F在BC上,连接DF,且AD=DF.
(Ⅰ)求证:CF=AE;
(Ⅱ)若AE=3,BF=4,求AB的长.
【解析】(Ⅰ)通过HL证明Rt△CDF≌Rt△EDA,即可得出结论;
(Ⅱ)通过HL证明△BED≌△BCD,得BE=BC,再进行等量代换即可.
证明:(Ⅰ)∵∠C=90°,AD是∠BAC的平分线,DE⊥AB,
∴DE=DC,∠AED=90°,
在Rt△CDF与Rt△EDA中,
,
∴Rt△CDF≌Rt△EDA(HL),
∴CF=AE;
(Ⅱ)∵CF=AE,AE=3,
∴CF=3,
∵BF=4,
∴BC=BF+CF=4+3=7,
∵DE⊥AB,
∴∠DEB=90°,
∵∠C=90°,
∴∠DEB=∠C,
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD,
在△BED和△BCD中,
,
∴△BED≌△BCD(AAS),
∴BE=BC=7,
∴AB=BE+AE=7+3=10.
例1-2.如图,点B在线段AC上,BD∥CE,AB=EC,DB=BC.求证:AD=EB.
【解析】由平行线的性质可得∠A=∠EBC,由“AAS”可证△ABD≌△BEC,可得BD=EC.
证明:∵BD∥CE,
∴∠ABD=∠C,
在△ABD和△ECB中,
∴△ABD≌△ECB(SAS),
∴AD=EB.
【针对训练】
1.已知:如图,AB∥DE,AB=DE,AF=DC.求证:∠B=∠E.
【解析】由AF=DC,得AC=DF,由AB∥DE,得∠A=∠D,即可证△ABC≌△DEF(SAS),故∠B=∠E.
证明:∵AF=DC,
∴AF+CF=DC+CF,即AC=DF,
∵AB∥DE,
∴∠A=∠D,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠B=∠E.
2.如图,在中,,、分别为、上一点,.若,求证:.
【答案】见解析
【解析】先根据条件得出,,再根据判定,即可得到.
解:证明:,
,
,
,
,,
,
在与中,
,
,
.
【点睛】本题主要考查了全等三角形的判定与性质、等腰三角形的性质等知识;熟练掌握等腰三角形的性质,证明三角形全等是解题的关键.
3.如图,CA=CD,CB=CE,AB=DE,AB与DE交于点M.
(1)求证:∠ACD=∠BCE;
(2)连MC,若∠BMC=78°,求∠BMD的度数.
【解析】(1)根据SSS证明△ABC≌△DEC,进而利用全等三角形的性质解答即可;
(2)根据AAS证明△AGC≌△DHC,进而利用全等三角形的性质解答即可.
证明:(1)在△ABC和△DEC中,
,
∴△ABC≌△DEC(SSS),
∴∠ACB=∠DCE,
∴∠ACD=∠BCE;
(2)过C作CG⊥AB于G,CH⊥DE于H,
∵△ABC≌△DEC,
∴∠A=∠D,AC=DC,
∵∠AGC=∠DHC=90°,
在△AGC和△DHC中,
,
∴△AGC≌△DHC(AAS),
∴CG=CH,
∴MC平分∠BMD,
∴∠BMD=2∠BMC=2×78°=156°.
类型二、全等三角形在证明线段和差关系的应用
【典例剖析】
例2-1.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
【解析】(1)①由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,推出∠DAC=∠BCE,根据AAS即可得到答案;
②由(1)得到AD=CE,CD=BE,即可求出答案;
(2)与(1)证法类似可证出∠ACD=∠EBC,能推出△ADC≌△CEB,得到AD=CE,CD=BE,代入已知即可得到答案.
(1)①证明:∵AD⊥DE,BE⊥DE,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中
,
∴△ADC≌△CEB(AAS).
②证明:由(1)知:△ADC≌△CEB,
∴AD=CE,CD=BE,
∵DC+CE=DE,
∴AD+BE=DE.
(2)证明:∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中
,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=EC-CD=AD-BE.
例2-2.综合与实践:
数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
(1)发现问题:如图1,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=30°,连接BE,CF,延长BE交CF于点D.则BE与CF的数量关系:_____,∠BDC=_____°;
(2)类比探究:如图2,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=120°,连接BE,CF,延长BE,FC交于点D.请猜想BE与CF的数量关系及∠BDC的度数,并说明理由;
(3)拓展延伸:如图3,△ABC和△AEF均为等腰直角三角形,∠BAC=∠EAF=90°,连接BE,CF,且点B,E,F在一条直线上,过点A作AM⊥BF,垂足为点M.则BF,CF,AM之间的数量关系:_____;
【答案】(1)BE=CF;(2)30;(3)BF=CF+2AM;
【解析】(1)根据等腰三角形的性质,利用SAS证明△ABE≌△ACF即可得出结论;
(2)根据等腰三角形的性质,利用SAS证明△BAE≌△CAF即可得出结论;
(3)根据等腰直角三角形的性质,利用SAS证明△BAE≌△CAE即可得出结论;
(4)根据直径所对的圆周角是直角,先找到点P,利用勾股定理计算出BP,再利用第3小题的结论得到三角形的高,△ABP的面积即可求出.
解:(1)BE=CF,∠BDC=30°,
理由如下:如图1所示:
∵△ABC和△ADE都是等腰三角形,
∴AB=AC,AE=AF,
又∵∠BAC=∠EAF=30°,
∴△ABE≌△ACF(SAS),
∴BE=CF,
∴∠ABE=∠ACD,
∵∠AOE∠ABE+∠BAC,
∠AOE=∠ACD+∠BDC,
∴∠BDC=∠BAC=30°;
(2)BE=CF,∠BDC=60°,
理由如下:如图2所示:
证明:∵∠BAC=∠EAF=120°,
∴∠BAC-∠EAC=∠EAF-∠EAC,
即∠BAE=∠CAF,
又∵△ABC和△AEF都是等腰三角形,
∴AB=AC,AE=AF,
∴△BAE≌△CAF(SAS)
∴BE=CF,
∴∠AEB=∠AFC,
∵∠EAF=120°,AE=AF,
∴∠AEF=∠AFE=30°,
∴∠BDC=∠BEF-∠EFD=∠AEB+30°-(∠AFC-30°)=60°;
(3)BF=CF+2AM,
理由如下:如图3所示:
∵△ABC和△AEF都是等腰三角形,
∴∠CAB=∠EAF=90°,AB=AC,AE=AF,
∴∠CAB-∠CAE=∠FAE-∠CAE,
即:∠BAE=∠CAF,
∴△BAE≌△CAE(SAS),
∴BE=CF,
∵AM⊥BF,AE=AF,EAF=90°,
∴EF=2AM,
∵BF=BE+EF,
∴BF=CF+2AM;
【针对训练】
1.已知:四边形中,,,,对角线相交于点O,且平分,过点A作,垂足为H.判断线段之间的数量关系:___________;并证明你的结论.
【答案】,证明见解析
【解析】先证明是等边三角形,再证明,最后根据三角形内角和定理证明,在上截取,先证明,得出,再证明,得出,即可解决问题.
,
证明:∵,,
∴是等边三角形,
∴,
∵,平分,
∴,
∴,
∵,,,
∴,
在上截取,
∵,
∴,
又,
∴,
∴,
∴
∵,
∴,
∴,
∵,
∴.
【点睛】此题主要考查了全等三角形的判定和性质、等边三角形的判定和性质,三角形内角和定理,角平分线的定义等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
2.如图1,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE.连结BE,CD,作AF⊥CD,垂足为F,交BE于点G.
(1)若∠GAE=70°,求∠ADC的度数;
(2)如图2,作EH⊥GF,垂足为H,HF=7,求EH+DF的长;
(3)求证:BG=EG.
【解析】(1)由∠ADC+∠DAF=90°,∠GAE+∠DAF=90°,得∠ADC=∠GAE=70°;
(2)可证明△EAH≌△ADF,EH=AF,AH=DF,则EH+DF=AF+AH=HF=7;
(3)作EH⊥FG于点H,BI⊥FG交FG的延长线于点I,可证明△BAI≌△ACF,得BI=AF,而EH=AF,所以BI=EH,可证明△BGI≌△EGH,则BG=EG.
(1)解:如图1,∵AF⊥CD,
∴∠AFD=90°,
∴∠ADC+∠DAF=90°,
∵∠DAE=90°,
∴∠GAE+∠DAF=90°,
∴∠ADC=∠GAE=70°,
∴∠ADC的度数是70°.
(2)解:如图2,∵EH⊥GF,
∴∠EHA=∠AFD=90°,
由(1)得∠EAH=∠ADF,
在△EAH和△ADF中,
,
∴△EAH≌△ADF(AAS),
∴EH=AF,AH=DF,
∴EH+DF=AF+AH=HF=7,
∴EH+DF的长是7.
(3)证明:如图3,作EH⊥FG于点H,BI⊥FG交FG的延长线于点I,
∴∠I=∠EHG=∠AFC=90°,
∵∠BAC=90°,
∴∠BAI=∠ACF=90°-∠CAF,
在△BAI和△ACF中,
,
∴△BAI≌△ACF(AAS),
∴BI=AF,
由(2)得EH=AF,
∴BI=EH,
在△BGI和△EGH中,
,
∴△BGI≌△EGH(AAS),
∴BG=EG.
3.如图,AD是△ABC的中线,BE⊥AD,垂足为E,CF⊥AD,交AD的延长线于点F,G是DA延长线上一点,连接BG.
(1)求证:BE=CF;
(2)若BG=CA,求证:GA=2DE.
【解析】(1)利用AAS证明△BED≌△CFD,得BE=CF;
(2)利用HL证明Rt△BGE≌Rt△CAF,得GE=AF,从而解决问题.
证明:(1)∵AD是△ABC的中线,
∴BD=CD,
∵BE⊥AD,CF⊥AD,
∴∠BED=∠F,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),
∴BE=CF;
(2)在Rt△BGE和Rt△CAF中,
,
∴Rt△BGE≌Rt△CAF(HL),
∴GE=AF,
∴AG=EF.
∵△BED≌△CFD,
∴DE=DF,
∴GA=2DE.
类型三、全等三角形在证明线段位置关系的应用
【典例剖析】
例3-1.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
【解析】(1)根据平行线性质求出∠A=∠B,根据SAS推出即可.
(2)根据全等三角形性质推出CD=CE,根据等腰三角形性质求出即可.
证明:(1)∵AD∥BE,
∴∠A=∠B,
在△ACD和△BEC中
∴△ACD≌△BEC(SAS),
(2)∵△ACD≌△BEC,
∴CD=CE,
又∵CF平分∠DCE,
∴CF⊥DE.
例3-2.已知AB=CD,AD=BC.求证:
①AD∥BC;
②∠B=∠D.
【解析】①连接AC,由AB=CD,BC=DA,AC=CA,根据全等三角形的判定定理“SSS”证明△ABC≌△CDA,得∠ACB=∠CAD,则AD∥BC;
②由△ABC≌△CDA,得∠B=∠D.
证明:①连接AC,
在△ABC和△CDA中,
,
∴△ABC≌△CDA(SSS),
∴∠ACB=∠CAD,
∴AD∥BC.
②△ABC≌△CDA,
∴∠B=∠D.
【针对训练】
1.两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:DC⊥BE.
【解析】(1)根据等腰直角三角形的性质,可以得出△ABE≌△ACD;
(2)由△ABE≌△ACD可以得出∠B=∠ACD-45°,进而得出∠DCB=90°,就可以得出结论.
(1)△ABE≌△ACD.
证明:∵△ABC与△AED均为等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°.
∴∠BAC+∠CAE=∠EAD+∠CAE.
即∠BAE=∠CAD,
在△ABE与△ACD中,
,
∴△ABE≌△ACD;
(2)证明∵△ABE≌△ACD,
∴∠ACD=∠ABE=45°,
又∵∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=90°,
∴DC⊥BE.
2.如图,,,,在同一条直线上,于点,于点,,,求证:.
【答案】见解析
【解析】先证明,利用全等三角形的性质解题即可.
证明:∵,
∴,
又∵
∴
在和中,
,
∴
∴
∴
【点睛】本题考查全等三角形的判定和性质,平行线的判定,掌握全等三角形的判定方法是解题的关键.
3.如图,点A,B,C,D在一条直线上,AB=CD,CE∥BF,CE=BF,求证:AE∥DF.
【解析】根据平行线的性质得出∠ACE=∠DBF,求出AC=BD,根据全等三角形的判定得出△AEC≌△DFB,根据全等三角形的性质得出∠A=∠D,根据平行线的判定得出即可.
证明:∵CE∥BF,
∴∠ACE=∠DBF,
∵AB=CD,
∴AB+BC=CD+BC,
即AC=BD,
在△AEC和△DFB中,
,
∴△AEC≌△DFB(SAS),
∴∠A=∠D,
∴AE∥DF.
类型四、全等三角形在线段或角的计算中的应用
【典例剖析】
例4-1.如图,,.
(1)求证:;
(2)若,.求的度数.
答案:(1)见详解
(2)
解析:(1)证明:在与中,
,
,
;
(2),
,
,.
,
.
例4-2.如图,在中,AD是BC边上的中线,E是AB边上一点,过点C作交ED的延长线于点F,
(1)求证:;
(2)当,,时,求AC的长.
(1)答案:见解析
解析:,
,,
是边上的中线,
,
;
(2)答案:3
解析:,
,
,
,,
.
【针对训练】
1.如图.点A,B,C,D在同一条直线上,点E,F分别在直线的两侧,且,,.
(1)求证:;
(2)若,,求的长.
答案:(1)见解析
(2)4
解析:(1)在和中,
,
;
(2),,
,
又,
.
2.如图,四边中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
答案:(1)见解析
(2)3
解析:(1),
,
即:,
在和中,
,
,
;
(2),
,
,,
.
3.如图,以的两边AC,BC为边分别向外作和,使得,,.
(1)求证:;
(2)若,,求的度数.
答案:(1)见解析
(2)
解析:(1)证明:,
,
即.
又,,
;
(2)由(1)得,
,,
.
,
,
.
4.如图,C是线段AB的中点,CD平分,CE平分,.
(1)求证:;
(2)若,求的度数.
答案:(1)证明见解析;
(2).
解析:(1)点C是线段AB的中点,
,
又平分,CE平分,
,,
在和中,
(2)
.
类型五、全等三角形在生活实际中的应用
【典例剖析】
例5-1.小明在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆点O处用一根细绳悬挂一个小球A,小球A可以自由摆动,如图,OA表示小球静止时的位置.当小明用发声物体靠近小球时,小球从OA摆到OB位置,此时过点B作BD⊥OA于点D,当小球摆到OC位置时,OB与OC恰好垂直(图中的A、B、O、C在同一平面上),过点C作CE⊥OA于点E,测得CE=15cm,OE=8cm.
(1)试说明:OE=BD;
(2)求DE的长.
【解析】(1)利用AAS证明△COE≌△OBD,可得结论;
(2)利用全等三角形性质可得答案.
解:(1)∵OB⊥OC,
∴∠BOD+∠COE=90°,
∵CE⊥OA,BD⊥OA,
∴∠CEO=∠ODB=90°,
∴∠BOD+∠B=90°,
∴∠COE=∠B,
∵OC=BO,
∴△COE≌△OBD(AAS),
∴OE=BD;
(2)∵△COE≌△OBD,
∴CE=OD=15cm,
∴DE=OD-OE=7cm.
例5-2.如图,小明在游乐场玩两层型滑梯,每层楼梯的高度相同(EH=HD),都为2.5米,他想知道左右两个滑梯BC和EF的长度是否相等,于是制定了如下方案:
课题 探究两个滑梯的长度是否相等
测量工具 长度为6米的米尺
测量步骤 ①测量出线段FD的长度
②测量出线段AB的长度
测量数据 DF=2.5米,AB=5米
(1)根据小明的测量方案和数据,判断两个滑梯BC和EF的长度是否相等?并说明理由.
(2)试猜想左右两个滑梯BC和EF所在直线的位置关系,并加以证明.
【解析】(1)证明△BAC≌△EDF(SAS),由全等三角形的性质得出BC=EF;
(2)延长BC交EF于点M,由全等三角形的性质得出∠BMF=90°,则可得出结论.
解:(1)BC=EF.
理由:∵EH=DH=2.5米,
∴ED=5米,
∴AB=DE,
由题意可知四边形CADH为矩形,
∴CA=DH=2.5米,
∵DF=2.5米,
∴CA=DF,
∵∠BAC=∠EDF=90°,
∴△BAC≌△EDF(SAS),
∴BC=EF;
(2)BC⊥EF.
理由:延长BC交EF于点M,
∵∠EDF=90°,
∴∠F+∠EDF=90°,
∵△BAC≌△EDF,
∴∠B=∠DEF,
∴∠B+∠F=90°,
∴∠BMF=90°,
∴EF⊥BM.
【针对训练】
1.如图,小明站在堤岸凉亭A点处,正对他的S点停有一艘游艇,他想知道凉亭与这艘游艇之间的距离,于是制定了如下方案.
课题 测凉亭与游艇之间的距离
测量工具 皮尺等
测量方案示意图
测量步骤 ①小明沿堤岸走到电线杆B旁;
②再往前走相同的距离,到达C点;
③然后他向左直行,当看到电线杆与游艇在一条直线上时停下来.
测量数据 AB=10米,BC=10米,CD=5米
(1)凉亭与游艇之间的距离是 _____米.
(2)请你说明小明做法的正确性.
【答案】5
【解析】根据全等三角形的判定和性质即可得到结论.
解:(1)凉亭与游艇之间的距离是5米;
故答案为:5.
(2)理由:在△ABS与△CBD中,
,
∴△ABS≌△CBD(ASA),
∴AS=CD=5米.
2.如图,这是王玲家的养鱼塘,王玲想要测量鱼塘的宽AB,请你帮助她设计一个不必下水而且简单可行的方案,并说明理由,要求在原图上画出该方案的示意图.
【解析】方案设计为:从A点出发沿与AB垂直的方向到C点,再沿AC方向走到D点,使CD=AC,接着从B点出发,沿与AD垂直的方向走到E点,使E、C、B共线,则测出DE的长解能得到AB的宽;然后根据全等三角形的判断方法证明△ACB≌△DCE,从而得到AB=DE.
解:方案设计为:
从A点出发沿与AB垂直的方向到C点,再沿AC方向走到D点,使CD=AC,接着从B点出发,沿与AD垂直的方向走到E点,使E、C、B共线,则测出DE的长解能得到AB的宽.
理由如下:∵AD⊥AB,BE⊥AD,
∴∠BAC=∠EDC,
∵∠BCA=∠ECD,AC=DC,
∴△ACB≌△DCE(ASA),
∴AB=DE.
3.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
【解析】∠BAD与∠CAD相等,证角相等,常常通过把角放到两个全等三角形中来证,本题OA=OA公共边,可考虑SSS证明三角形全等,从而推出角相等.
解:雨伞开闭过程中二者关系始终是:∠BAD=∠CAD,
理由如下:
∵AB=AC,AE=AB,AF=AC,
∴AE=AF,
在△AOE与△AOF中,
,
∴△AOE≌△AOF(SSS),
∴∠BAD=∠CAD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
