人教版八年级数学上名师点拨精练 12.3角平分线的性质(1) (含解析)
文档属性
| 名称 | 人教版八年级数学上名师点拨精练 12.3角平分线的性质(1) (含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-07 23:47:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.3 角平分线的性质(1)
学习目标
1.通过全等三角形的知识理解角平分线的定理。
2.会利用尺规作一个角的角平分线。
3.在利用尺规作图的过程中培养学生的动手操作能力。
4.能运用角的平分线性质定理解决简单的几何问题。
【学习重难点】
角的平分线的性质的证明及运用。
老师告诉你
运用角的平分线的性质解决与面积有关问题的方法:
首先运用三角形的面积公式将面积关系转化为线段关系,再结合角的平分线的性质进一步转化为三角形的边长之间的关系,从而把两者建立起关系,结合已知条件可解决问题。
知识点拨
知识点1 作已知角的平分线
已知:∠AOB.
求作:∠AOB 的平分线.
作法:(1) 以点 O 为圆心,适当长为半径画弧,交 OA 于点 M,交 OB 于点 N;
(2) 分别以点 M、N 为圆心,大于MN 的长为半径画弧,两弧在∠AOB 的内部相交于点 C;
(3) 画射线 OC. 则射线 OC 即为所求.
【注意】(1)以小于MN 的长为半径画弧时,两弧没有交点.(2)不能说成“连接OC”.
【新知导学】
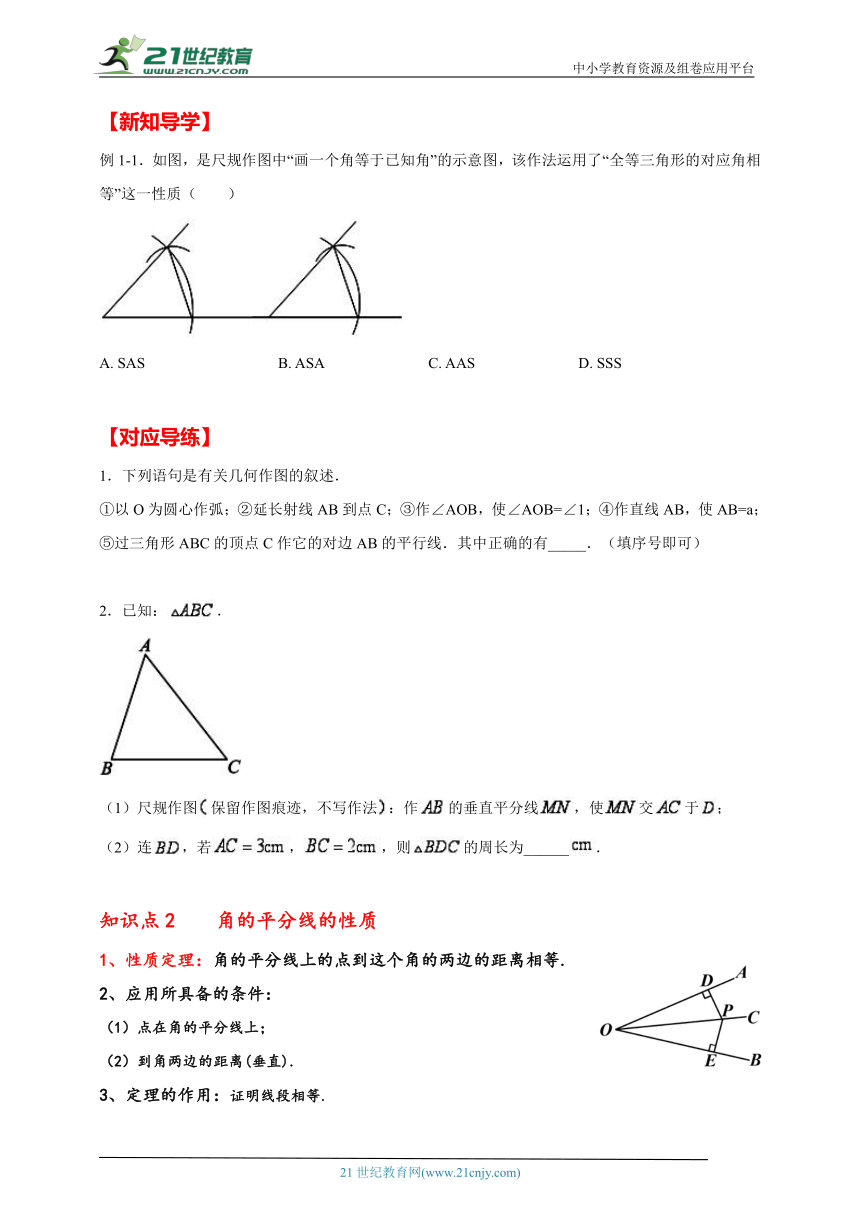
例1-1.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质( )
A. SAS B. ASA C. AAS D. SSS
【对应导练】
1.下列语句是有关几何作图的叙述.
①以O为圆心作弧;②延长射线AB到点C;③作∠AOB,使∠AOB=∠1;④作直线AB,使AB=a;⑤过三角形ABC的顶点C作它的对边AB的平行线.其中正确的有_____.(填序号即可)
2.已知:.
(1)尺规作图保留作图痕迹,不写作法:作的垂直平分线,使交于;
(2)连,若,,则的周长为______.
知识点2 角的平分线的性质
1、性质定理:角的平分线上的点到这个角的两边的距离相等.
2、应用所具备的条件:
(1)点在角的平分线上;
(2)到角两边的距离(垂直).
3、定理的作用:证明线段相等.
4、角平分线的性质的几何语言:
如图,∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PD=PE
【注意】①这里的距离是指点到角的两边垂线段的长;②该性质可以独立作为证明两条线段相等的依据,有时不必证明全等;③使用该结论的前提条件是图中有角平分线,有垂直.
【新知导学】
例2-1.如图,点D在的边上,且.
(1)作的平分线,交于点E(用尺规作图,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线与直线的位置关系,并说明理由.
【对应导练】
1.如图,,平分,交于C.
(1)尺规作图:过点B作的垂线,交于O,交于D,(保留作图痕迹,不写作法);
(2)求证:.
2.如图,中,点D在BC边上,,的平分线交AC于点E,过点E作,交BA的延长线于F,且,连接DE.
(1)求的度数;
(2)求证:DE平分;
(3)若,,,且,求的面积.
3.如图1,在中,,,AD,CE分别是,的平分线,AD,CE相交于点F.
(1)判断FE与FD之间的数量关系,并说明理由;
(2)如图2,如果不是直角,其他条件不变,(1)中所得结论是否仍然成立?请说明理由.
4.如图,已知BD是的平分线,,点P在BD上,,,垂足分别为M,N.试说明.
5.如图,中,平分,且,于E,于F,
(1)求证:与互补;
(2)如果,求的长.
题型训练
利用角平分线的作图在证明线段相等的应用
1.如图,四边形ABCD中,,,M为BC边上一点,且AM平分,DM平分.
求证:(1);
(2)M为BC的中点.
2.如图,已知BD是的平分线,,点P在BD上,,,垂足分别为M,N.试说明.
利用角平分线的性质求面积
3.如图,在中,的平分线相交于点O,连接OA,.求.
4.如图,在中,.
(1)过点B作的平分线交AC于点D(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);
(2)若,,求的面积.
利用角平分线的性质探究角的数量关系
5.如图13-1,已知BD是的角平分线,,交BD的延长线于点E.
(1)若.
①求和的度数
②求证:;
(2)如图13-2,AO平分,请直接写出与之间的数量关系.
6.如图,已知,AC平分,点B、D分别在AN、AM上.
(1)如图①,若,请你探索线段AD、AB、AC之间的数量关系,并给出证明;
(2)如图②,若,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
7.如图,,BD平分.求证:.
8.如图,在中,,为延长线上一点,,的平分线与交于点,连接.
(1)求证:点到的距离相等;
(2)求的度数.
牛刀小试
一、单选题(每小题4分,共32分)
1.下列尺规作图的语句错误的是( )
A. 作∠AOB,使∠AOB=∠α
B. 以点A为圆心,线段a的长为半径作弧
C. 作∠ABC,使∠ABC=∠α+∠β
D. 在∠AOC的边OC上用刻度尺截取5cm
2.如图,在Rt△ABC中,∠C=90°,以点A为圆心,适当长为半径作弧,分别交AB,AC于点D,E,再分别以点D,E,为圆心,以大于DE的长度为半径作弧,两弧交于点F,作射线AF交BC于点G,若AB=12,CG=3,则△ABG的面积是( )
A. 12 B. 18 C. 24 D. 36
3.如图,电信部门要修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路CD和EF的距离也必须相等.发射塔应该修建在( )
A. ∠AOB、∠COF两角的角平分线的交点
B. ∠COF的角平分线与线段AB的垂线平分线的交点
C. ∠DOF的角平分线与线段AB的垂线平分线的交点
D. ∠DOF、∠COF两角的角平分线分别与线段AB的垂线平分线的交点
4.如图,已知OC平分∠AOB,P是OC上任意一点,PD∥OA交OB于点D,PE⊥OA于点E,∠AOB=30°,如果PE=4,则OD的长为( )
A. 4 B. 6 C. 7 D. 8
5.如图,已知BP是∠ABC的平分线,AP⊥BP,若S△BPC=10cm2,则△ABC的面积等于( )
A. 20cm2 B. 30cm2 C. 25cm2 D. 不能确定
6.如图,在等边△ABC中,∠ABC和∠ACB的角平分线交于点D,过点D作EF//BC分别交AB、AC于点E、F,若EF=2,则△ABC的周长是( )
A. 10 B. 9 C. 8 D. 6
7.如图,AM垂直∠ABC的平分线BM于点M,D为BC中点,连接MD,若△ABC的面积为4,则△BMD的面积为( )
A. 1 B. 2 C. 2.5 D. 3
8.如图,点P为定角∠AOB平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论中,不正确的是( )
A. OM+ON的值不变 B. ∠PNM=∠POB
C. MN的长不变 D. 四边形PMON的面积不变
二、填空题(每小题4分,共20分)
9.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=20,则CD=_____.
10.如图,在Rt△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心,以小于AC长为半径作弧,分别交AC,AB于点M,N;②分别以M,N为圆心,以大于MN的长为半径作弧,在∠BAC内两弧交于点O;③作射线AO,交BC于点D.若点D到AB的距离为1,则CD的长为 _____.
11.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的是______.
①线段AD是△ABC的角平分线; ②∠ADC=60°;
③点D在AB的中垂线上; ④.
12.如图,在中,交于点,平分交于点,的面积为4,的面积为8,,则的长为 _____.
13.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,AB=6cm,则△DEB的周长为 _____.
三、解答题(共6小题,共48分)
14.(8分)如图,在△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,点F在BC上,连接DF,且AD=DF.
(Ⅰ)求证:CF=AE;
(Ⅱ)若AE=3,BF=4,求AB的长.
15.(8分)如图,△ABC 中,点D在边AC上,且AD=AB.
(1)请用无刻度的直尺和圆规作出∠A的平分线(保留作图痕迹,不写作法);
(2)若(1)中所作的角平分线与边BC交于点E,连接DE.求证:DE=BE.
16.(8分)如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=.
(1)尺规作图:作∠BAC的角平分线交BC于点P(不写作法,保留作图痕迹);
(2)在(1)所作图形中,求△ABP的面积.
17.(8分)如图,在中,为其角平分线,于点,于点,的面积是,,,求的长.
18.(8分)如图①,在△ABC中,AD是它的角平分线,P是AD上一点,PE∥AB交BC于E,PF∥AC交BC于F.
(1)求证:D到PE的距离与D到PF的距离相等;
(2)如图②,若点P在AD的延长线上,其他条件不变,试猜想(1)中的结论还成立吗?请证明你的猜想.
19 .(8分)在△ABC中,D是BC边上的点(不与点B、C重合),连接AD.
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD= ;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示);
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC= .
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.3 角平分线的性质(1)
学习目标
1.通过全等三角形的知识理解角平分线的定理。
2.会利用尺规作一个角的角平分线。
3.在利用尺规作图的过程中培养学生的动手操作能力。
4.能运用角的平分线性质定理解决简单的几何问题。
【学习重难点】
角的平分线的性质的证明及运用。
老师告诉你
运用角的平分线的性质解决与面积有关问题的方法:
首先运用三角形的面积公式将面积关系转化为线段关系,再结合角的平分线的性质进一步转化为三角形的边长之间的关系,从而把两者建立起关系,结合已知条件可解决问题。
知识点拨
知识点1 作已知角的平分线
已知:∠AOB.
求作:∠AOB 的平分线.
作法:(1) 以点 O 为圆心,适当长为半径画弧,交 OA 于点 M,交 OB 于点 N;
(2) 分别以点 M、N 为圆心,大于MN 的长为半径画弧,两弧在∠AOB 的内部相交于点 C;
(3) 画射线 OC. 则射线 OC 即为所求.
【注意】(1)以小于MN 的长为半径画弧时,两弧没有交点.(2)不能说成“连接OC”.
【新知导学】
例1-1.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质( )
A. SAS B. ASA C. AAS D. SSS
【答案】D
【解析】利用作图的基本原理,得到线段的关系证明即可.
解:如图,由作图可知,BA=CF.
在△AOB和△CEF中,,
∴△AOB≌△CEF(SSS),
故选:D.
【对应导练】
1.下列语句是有关几何作图的叙述.
①以O为圆心作弧;②延长射线AB到点C;③作∠AOB,使∠AOB=∠1;④作直线AB,使AB=a;⑤过三角形ABC的顶点C作它的对边AB的平行线.其中正确的有_____.(填序号即可)
【答案】③⑤
【解析】①根据确定圆的两个条件:圆心和半径判断即可;
②根据射线的性质判断即可;
③根据基本作图:作一个角等于已知角判断即可;
④根据直线的性质判断即可;
⑤根据平行公理判断即可.
解:①以O为圆心作弧可以画出无数条弧,因为半径不固定,所以叙述错误;
②射线AB是由A向B向无限延伸,所以叙述错误;
③根据作一个角等于已知角的作法,可以作一个角∠AOB,使∠AOB等于已知∠1,所以叙述正确;
④直线可以向两方无限延伸,所以叙述错误;
⑤根据平行公理:过直线外一点有且只有一条直线与已知直线平行,可以过三角形ABC的顶点C作它的对边AB的平行线,所以叙述正确.
所以正确的有③⑤.
故答案为:③⑤.
2.已知:.
(1)尺规作图保留作图痕迹,不写作法:作的垂直平分线,使交于;
(2)连,若,,则的周长为______.
【答案】(1)见解析 (2)5
【解析】对于(1),分别以A、B两点为圆心,以大于长度为半径画弧,在两边分别相交于两点,然后过这两点作直线,即为的垂直平分线;
对于(2),根据线段垂直平分线的性质得出,再根据周长公式即可得出答案.
【小问1详解】
作图如图所示:
【小问2详解】
的垂直平分线,
.
,,
的周长是:(cm).
故答案为:.
【点睛】本题主要考查了尺规作图和线段垂直平分线的性质,解题的关键是掌握“垂直平分线上的点到这条线段两端点的距离相等”.
知识点2 角的平分线的性质
1、性质定理:角的平分线上的点到这个角的两边的距离相等.
2、应用所具备的条件:
(1)点在角的平分线上;
(2)到角两边的距离(垂直).
3、定理的作用:证明线段相等.
4、角平分线的性质的几何语言:
如图,∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PD=PE
【注意】①这里的距离是指点到角的两边垂线段的长;②该性质可以独立作为证明两条线段相等的依据,有时不必证明全等;③使用该结论的前提条件是图中有角平分线,有垂直.
【新知导学】
例2-1.如图,点D在的边上,且.
(1)作的平分线,交于点E(用尺规作图,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线与直线的位置关系,并说明理由.
答案:
解:(1)如图.
(2)理由如下:
平分
.
,
.
.
【对应导练】
1.如图,,平分,交于C.
(1)尺规作图:过点B作的垂线,交于O,交于D,(保留作图痕迹,不写作法);
(2)求证:.
答案:(1)解:如图为所作
(2)证明:,
平分,
,
,平分,
.
2.如图,中,点D在BC边上,,的平分线交AC于点E,过点E作,交BA的延长线于F,且,连接DE.
(1)求的度数;
(2)求证:DE平分;
(3)若,,,且,求的面积.
答案:(1)解:,,
.
,.
(2)证明:过点E作于G,于H,如图.
,,,
.
BE平分,,,
,.
,,DE平分.
(3)解:,
,即,解得,
,
的面积为.
3.如图1,在中,,,AD,CE分别是,的平分线,AD,CE相交于点F.
(1)判断FE与FD之间的数量关系,并说明理由;
(2)如图2,如果不是直角,其他条件不变,(1)中所得结论是否仍然成立?请说明理由.
答案:(1).理由如下:
过点F作于点M, 于点N,则,
,,
,的平分线AD,CE交于点F,
点F在的平分线上,
又,
(2)成立.理由如下:
过点F作于点M, 于点N,
则,,
,,
4.如图,已知BD是的平分线,,点P在BD上,,,垂足分别为M,N.试说明.
答案:BD平分,,
又,,
,.
又,,
.
5.如图,中,平分,且,于E,于F,
(1)求证:与互补;
(2)如果,求的长.
答案:(1)略 (2)
题型训练
利用角平分线的作图在证明线段相等的应用
1.如图,四边形ABCD中,,,M为BC边上一点,且AM平分,DM平分.
求证:(1);
(2)M为BC的中点.
答案:证明:(1),,
AM平分,DM平分,
,
,
,即.
(2)如图,过M作,垂足为点N,
,,
,,
AM平分,DM平分,
,,
,即M为BC的中点.
2.如图,已知BD是的平分线,,点P在BD上,,,垂足分别为M,N.试说明.
答案:BD平分,,
又,,
,.
又,,
.
利用角平分线的性质求面积
3.如图,在中,的平分线相交于点O,连接OA,.求.
答案:解:如图,过点O作,垂足分别为点D,E,F.
由三角形三条角平分线的性质定理,可知.
,
.
4.如图,在中,.
(1)过点B作的平分线交AC于点D(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);
(2)若,,求的面积.
答案:(1)图见解析
(2)的面积24
解析:(1)的平分线如图中BD所示.
(2)如图,过点D作于H.
平分,,,
,
的面积
.
利用角平分线的性质探究角的数量关系
5.如图13-1,已知BD是的角平分线,,交BD的延长线于点E.
(1)若.
①求和的度数
②求证:;
(2)如图13-2,AO平分,请直接写出与之间的数量关系.
答案:(1)①的度数为72°,的度数为18°;
②
由①可知
(2)
6.如图,已知,AC平分,点B、D分别在AN、AM上.
(1)如图①,若,请你探索线段AD、AB、AC之间的数量关系,并给出证明;
(2)如图②,若,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
答案:(1).
证明:AC平分,,
,
又,
,
则.
.
(2)仍然成立.
证明:如图,过点C分别作AM、AN的垂线,垂足分别为E、F,
AC平分,
(角平分线上的点到角两边的距离相等),
,,
,
又,
,
,,
由(1)可知,
.
7.如图,,BD平分.求证:.
答案:证明:过点D作BA、BC的垂线,垂足分别为E、F,则(角平分线上的点到这个角的两边的距离相等).
在和中,,
,
,
.
8.如图,在中,,为延长线上一点,,的平分线与交于点,连接.
(1)求证:点到的距离相等;
(2)求的度数.
答案:(1)如图,过点作于点于点,交的延长线于点,
平分,.
,,
,,
,点到的距离相等.
(2)由(1)知,平分.
平分.
.
牛刀小试
一、单选题(每小题4分,共32分)
1.下列尺规作图的语句错误的是( )
A. 作∠AOB,使∠AOB=∠α
B. 以点A为圆心,线段a的长为半径作弧
C. 作∠ABC,使∠ABC=∠α+∠β
D. 在∠AOC的边OC上用刻度尺截取5cm
【答案】C
【解析】根据基本作图的方法,逐项分析,从而得出结论.
解:A、作一个角等于已知角是常见的尺规作图,故不符合题意;
B、画弧既需要圆心,还需要半径,故不符合题意.
C、作一个角等于已知角,但不能等于两角的和,故符合题意;
D、在∠AOC的边OC上用刻度尺截取5cm,故不符合题意;
故选:C.
2.如图,在Rt△ABC中,∠C=90°,以点A为圆心,适当长为半径作弧,分别交AB,AC于点D,E,再分别以点D,E,为圆心,以大于DE的长度为半径作弧,两弧交于点F,作射线AF交BC于点G,若AB=12,CG=3,则△ABG的面积是( )
A. 12 B. 18 C. 24 D. 36
【答案】B
【解析】过点G作GH⊥AB于点H,根据题意得,AF是∠CAB的角平分线,得CG=GH,根据三角形面积公式,即可求出△ABG的面积.
解:过点G作GH⊥AB于点H,
根据题意得,AF是∠CAB的角平分线,
∵∠C=90°,
∴AC⊥CG,
∵GH⊥AB,
∴CG=GH,
∵CG=3,
∴,
故选:B.
3.如图,电信部门要修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路CD和EF的距离也必须相等.发射塔应该修建在( )
A. ∠AOB、∠COF两角的角平分线的交点
B. ∠COF的角平分线与线段AB的垂线平分线的交点
C. ∠DOF的角平分线与线段AB的垂线平分线的交点
D. ∠DOF、∠COF两角的角平分线分别与线段AB的垂线平分线的交点
【答案】B
【解析】由线段垂直平分线的性质可知:要两个城镇A,B的距离,发射塔必须建在线段AB的垂直平分线上,再根据角平分线的性质可知要到两条高速公路CD和EF的距离相等需要建在∠COF的平分线上,即可知发射塔要在两线的交点位置.
解:要两个城镇A,B的距离,发射塔必须建在线段AB的垂直平分线上,要到两条高速公路EF和CD的距离相等需要建在∠COF的平分线上,
∴发射塔应该修建在∠COF的平分线和线段AB的垂直平分线的交点处.
故选:B.
4.如图,已知OC平分∠AOB,P是OC上任意一点,PD∥OA交OB于点D,PE⊥OA于点E,∠AOB=30°,如果PE=4,则OD的长为( )
A. 4 B. 6 C. 7 D. 8
【答案】D
【解析】过P作PH⊥OB于H,由角平分线的性质得到PH=PE=4,由含30°角的直角三角形的性质得到PD=2PH=8,由平行线的性质,角平分线的定义推出∠DPO=∠DOP,因此OD=PD=8.
解:过P作PH⊥OB于H,
∵OC平分∠AOB,PE⊥AO,
∴PH=PE=4,
∵PD∥OA,
∴∠PDH=∠AOB=30°,
∴PD=2PH=8,
∵PD∥OA,
∴∠DPO=∠POE,
∵OC平分∠AOB,
∴∠DOP=∠POE,
∴∠DPO=∠DOP,
∴OD=PD=8.
故选:D.
5.如图,已知BP是∠ABC的平分线,AP⊥BP,若S△BPC=10cm2,则△ABC的面积等于( )
A. 20cm2 B. 30cm2 C. 25cm2 D. 不能确定
【答案】A
【解析】先延长AP交BC于点D,根据已知条件证明△BAP≌△BDP,从而证出AP=PD,根据等底同高面积相等,得到△APC的面积=△DPC的面积,最后根据△BPC的面积是12cm2,求出答案即可.
解:如图所示:延长AP交BC于点D,
∵BP是∠ABC的平分线,
∴∠ABP=∠DBP,
∵AP⊥BP,
∴∠APB=∠DPB=90°,
∵BP=BP,
∴△BAP≌△BDP(ASA),
∴AP=DP,
∴△APC的面积=△DPC的面积,
∵△BPC的面积=10(cm2),
∴△BPD的面积+△CPD的面积=10(cm2),
∴△ABP的面积+△APC的面积=10(cm2),
∴△ABC的面积=△BPD的面积+△CPD的面积+△ABP的面积+△APC的面积=20(cm2),
故选:A.
6.如图,在等边△ABC中,∠ABC和∠ACB的角平分线交于点D,过点D作EF//BC分别交AB、AC于点E、F,若EF=2,则△ABC的周长是( )
A. 10 B. 9 C. 8 D. 6
【答案】B
【解析】利用角平分线性质可得两组角相等,再结合平行线的性质,可证出∠OBE=∠EOB,∠OCF=∠COF,那么利用等角对等边可得线段的相等,再利用等量代换可求得EF=BE+CF.
解:∵BD、CD是∠ABC、∠ACB的角平分线,
∴∠DBE=∠DBC,∠DCF=∠BCD,
又∵EF∥BC,
∴∠DBC=∠BDE,∠BCD=∠CDF,
∴∠OBE=∠BOE,∠COF=∠OCF,
∴BE=DE,CF=DF,
∴EF=DE+DF=BE+CF=2,
∵△ABC是等边三角形,BE=1,
∴AB=BC=EF+BE=3,
∴△ABC的周长是9.
故选:B.
7.如图,AM垂直∠ABC的平分线BM于点M,D为BC中点,连接MD,若△ABC的面积为4,则△BMD的面积为( )
A. 1 B. 2 C. 2.5 D. 3
【答案】A
【解析】延长AM交BC于N,证明△AMB≌△NMB,根据全等三角形的性质得到AM=NM,根据三角形的面积公式计算即可.
解:延长AM交BC于N,
在△AMB和△NMB中,
,
∴△AMB≌△NMB(ASA),
∴AM=NM,
∴S△AMB=S△NMB,S△AMC=S△NMC,
∴S△BMC=S△ABC=2,
∵D为BC中点,
∴S△BMD=S△BMC=1,
故选:A.
8.如图,点P为定角∠AOB平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论中,不正确的是( )
A. OM+ON的值不变 B. ∠PNM=∠POB
C. MN的长不变 D. 四边形PMON的面积不变
【答案】C
【解析】过P作PL⊥OB于M,PQ⊥OA于N,可以证明△PMQ≌△PNL(AAS),得到PM=PN,MQ=LN,OQ=OL,因此OM+ON=MQ+OQ+OL-LN=2OQ=定值;设∠MPN=x°,
∠PNM=∠PON=90°-x°,由M、N在移动,得到MN的长在变化,四边形PMON的面积=四边形PQOL的面积=2×△POQ的面积=OQ PQ=定值.
解:过P作PL⊥OB于M,PQ⊥OA于N,
∵OP平分∠AOB,
∴PL=PQ,
∵∠MPN与∠AOB互补,
∴∠PMQ+∠PNO=180°,
∴∠PNL+∠PNO=180°,
∴∠PMQ=∠PNL,
∵∠PQM=∠PLN=90°,
∴△PMQ≌△PNL(AAS),
∴PM=PN,MQ=LN,OQ=OL,
∴OM+ON=MQ+OQ+OL-LN=2OQ,
∵∠AOB的度数是定值,OP的长是定值,
∴OQ的长是定值,
∴OM+ON的值不变,
故A不符合题意;
设∠MPN=x°,
∵PM=PN,
∴∠PNM=∠PMN=×(180°-x)=90°-x°,
∵∠AOB+∠MPN=180°,
∴∠AOB=180°-x°
∴∠PON=×(180°-x)=90°-x°,
∴∠PNM=∠PON,
故B不符合题意;
∵M、N在移动,
∴MN的长在变化,
故C符合题意;
∵△PMQ≌△PNL,
∴四边形PMON的面积=四边形PQOL的面积,
∵OP=OP,PQ=PL,
∴Rt△POQ≌Rt△POL(HL),
∴四边形PQOL的面积=2×△POQ的面积=OQ PQ,
∵OQ,PQ的长是定值,
∴四边形PMON的面积不变,
故D不符合题意.
故选:C.
二、填空题(每小题4分,共20分)
9.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=20,则CD=_____.
【答案】4
【解析】过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得DE=CD,然后利用△ABD的面积列式计算即可得解.
解:如图,过点D作DE⊥AB于点E;
∵∠C=90°,AD平分∠BAC,
∴CD=DE;
∵S△ABD=AB DE=×10 DE=20,
∴DE=4,
∴CD=DE=4.
故答案为:4.
10.如图,在Rt△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心,以小于AC长为半径作弧,分别交AC,AB于点M,N;②分别以M,N为圆心,以大于MN的长为半径作弧,在∠BAC内两弧交于点O;③作射线AO,交BC于点D.若点D到AB的距离为1,则CD的长为 _____.
【答案】1
【解析】根据角平分线的性质得到CD=点D到AB的距离=1.
解:由作图知AD平分∠BAC,
∵∠C=90°,点D到AB的距离为1,
∴CD=1.
故答案为:1.
11.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的是______.
①线段AD是△ABC的角平分线; ②∠ADC=60°;
③点D在AB的中垂线上; ④.
【答案】①②③④
【解析】先根据三角形内角和计算出∠BAC=60°,再利用基本作图对①进行判断;利用∠BAD=∠CAD=30°得到∠ADC=60°,则可对②进行判断;利用∠B=∠BAD得到DA=DB,根据线段垂直平分线的性质定理的逆定理可对③进行判断;利用30度角所对的直角边是斜边的一半、三角形的面积计算公式即可得出两个三角形的面积之比.
详解】解:由作法得,AD平分∠BAC,故①正确;
∵∠C=90°,∠B=30°,
∴∠BAC=60°,
∴,
∴,故②正确;
∵,
∴,
∴点D在AB的垂直平分线上,故③正确;
∵在直角△ACD中,∠CAD=30°,
∴,
∴,
,
∴,
∴,
∴.故④正确.
综上所述,正确的有①②③④.
故答案为:①②③④.
【点睛】本题考查了角平分线的性质、线段垂直平分线的性质以及作图-基本作图.解题时需要熟悉等腰三角形的判定与性质.
12.如图,在中,交于点,平分交于点,的面积为4,的面积为8,,则的长为 _____.
【答案】6
【解析】根据垂直的定义得到∠CHD=90°,根据三角形的面积求得DH=,过D作DE⊥BC于E,根据角平分线的性质得到DE=DH=,于是得到结论.
解:∵BH⊥AC,
∴∠CHD=90°,
∵△DCH的面积为4,CH=3,
∴DH=,
过D作DE⊥BC于E,
∵CD平分∠ACB交BH于点D
∴DE=DH=,
∵△BCD的面积为8,
∴DE BC=BC=8,
∴BC=6,
故答案为:6.
【点睛】本题考查了角平分线的性质,三角形的面积的计算,正确的作出辅助线是解题的关键.
13.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,AB=6cm,则△DEB的周长为 _____.
【答案】6cm
【解析】先利用角平分线的性质得到DC=DE,则△DEB的周长=BC+BE,再证明Rt△ACD≌Rt△AED得到AC=AE,所以△DEB的周长=AE+BE=AB.
解:∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴DC=DE,
∴△DEB的周长=DE+BE+BD=CD+BD+BE=BC+BE,
在Rt△ACD和Rt△AED中
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∵AC=BC,
∴AE=BC,
∴△DEB的周长=AE+BE=AB=6cm.
故答案为:6cm.
三、解答题(共6小题,共48分)
14.(8分)如图,在△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,点F在BC上,连接DF,且AD=DF.
(Ⅰ)求证:CF=AE;
(Ⅱ)若AE=3,BF=4,求AB的长.
【解析】(Ⅰ)通过HL证明Rt△CDF≌Rt△EDA,即可得出结论;
(Ⅱ)通过HL证明△BED≌△BCD,得BE=BC,再进行等量代换即可.
证明:(Ⅰ)∵∠C=90°,AD是∠BAC的平分线,DE⊥AB,
∴DE=DC,∠AED=90°,
在Rt△CDF与Rt△EDA中,
,
∴Rt△CDF≌Rt△EDA(HL),
∴CF=AE;
(Ⅱ)∵CF=AE,AE=3,
∴CF=3,
∵BF=4,
∴BC=BF+CF=4+3=7,
∵DE⊥AB,
∴∠DEB=90°,
∵∠C=90°,
∴∠DEB=∠C,
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD,
在△BED和△BCD中,
,
∴△BED≌△BCD(AAS),
∴BE=BC=7,
∴AB=BE+AE=7+3=10.
15.(8分)如图,△ABC 中,点D在边AC上,且AD=AB.
(1)请用无刻度的直尺和圆规作出∠A的平分线(保留作图痕迹,不写作法);
(2)若(1)中所作的角平分线与边BC交于点E,连接DE.求证:DE=BE.
【解析】(1)利用角平分线的作图步骤作图即可;
(2)证明△BAE≌△DAE(SAS),即可得出结论.
(1)解:如图所示,即为所求,
(2)证明:∵AE平分∠BAC,
∴∠BAE=∠DAE,
∵AB=AD,AE=AE,
∴△BAE≌△DAE(SAS),
∴DE=BE.
16.(8分)如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=.
(1)尺规作图:作∠BAC的角平分线交BC于点P(不写作法,保留作图痕迹);
(2)在(1)所作图形中,求△ABP的面积.
【解析】(1)根据角平分线的作法,即可画出图形;
(2)由勾股定理求出AC,由角平分线的性质得到PC=PD,根据三角形的面积公式求出PD,即可求出结论.
解:(1)如图所示:AP即为所求;
(2)在Rt△ABC中,∠ACB=90°,AB=5,BC=,
∴AC==2,
过点P作PD⊥AB于D,
∵AP是∠BAC的角平分线,
∴PD=PC,
∵△ABC的面积=△ACP的面积+△ABP的面积,
∴AC PC+AB PD=AC BC,
∴2PD+5PD=2,
解得PD=,
∴△ABP的面积=AB PD==.
17.(8分)如图,在中,为其角平分线,于点,于点,的面积是,,,求的长.
【答案】
【解析】根据角平分线上的点到角的两边距离相等可得,再根据,计算即可得解.
解:为的平分线,,,
,
∵,
∴,
即,
解得:,
.
【点睛】本题主要考查了角平分线上的点到角的两边距离相等的性质,三角形的面积,熟记性质并列出方程是解题的关键.
18.(8分)如图①,在△ABC中,AD是它的角平分线,P是AD上一点,PE∥AB交BC于E,PF∥AC交BC于F.
(1)求证:D到PE的距离与D到PF的距离相等;
(2)如图②,若点P在AD的延长线上,其他条件不变,试猜想(1)中的结论还成立吗?请证明你的猜想.
【分析】(1)首先由PE∥AB,PF∥AC,根据两直线平行,同位角相等,可得∠EPD=∠BAD,∠DPF=∠CAD,又由△ABC中,AD是它的角平分线,可得DP平分∠EPF,根据角平分线的性质,即可证得D到PE的距离与D到PF的距离相等;
(2)若点P在AD的延长线上,其他条件不变,(1)中的结论还成立,同(1)证明即可.
【解答】(1)证明:∵PE∥AB,PF∥AC,
∴∠EPD=∠BAD,∠DPF=∠CAD,
∵△ABC中,AD是它的角平分线,
∴∠BAD=∠CAD,
∴∠EPD=∠DPF,
即PD平分∠EPF,
∴D到PE的距离与D到PF的距离相等;
(2)若点P在AD的延长线上,其他条件不变,(1)中的结论还成立.理由如下:
∵PE∥AB,PF∥AC,
∴∠EPD=∠BAD,∠DPF=∠CAD,
∵△ABC中,AD是它的角平分线,
∴∠BAD=∠CAD,
∴∠EPD=∠DPF,
即PD平分∠EPF,
∴D到PE的距离与D到PF的距离相等.
【点评】此题考查了角平分线的性质与平行线的性质.此题难度不大,解题的关键是熟记角平分线的性质定理的应用,注意数形结合思想的应用.
19 .(8分)在△ABC中,D是BC边上的点(不与点B、C重合),连接AD.
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD= ;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示);
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC= .
【分析】(1)过A作AE⊥BC于E,根据三角形面积公式求出即可;
(2)过D作DE⊥AB于E,DF⊥AC于F,根据角平分线性质求出DE=DF,根据三角形面积公式求出即可;
(3)根据已知和(1)(2)的结论求出△ABD和△ACD的面积,即可求出答案.
【解答】解:(1)过A作AE⊥BC于E,
∵点D是BC边上的中点,
∴BD=DC,
∴SABD:S△ACD=(BD×AE):(CD×AE)=1:1,
故答案为:1:1;
(2)过D作DE⊥AB于E,DF⊥AC于F,
∵AD为∠BAC的角平分线,
∴DE=DF,
∵AB=m,AC=n,
∴SABD:S△ACD=(AB×DE):(AC×DF)=m:n;
(3)
∵AD=DE,
∴由(1)知:S△ABD:S△EBD=1:1,
∵S△BDE=6,
∴S△ABD=6,
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知:S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=3+6=9,
故答案为:9.
【点评】本题考查了角平分线性质和三角形的面积公式,能根据(1)(2)得出规律是解此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.3 角平分线的性质(1)
学习目标
1.通过全等三角形的知识理解角平分线的定理。
2.会利用尺规作一个角的角平分线。
3.在利用尺规作图的过程中培养学生的动手操作能力。
4.能运用角的平分线性质定理解决简单的几何问题。
【学习重难点】
角的平分线的性质的证明及运用。
老师告诉你
运用角的平分线的性质解决与面积有关问题的方法:
首先运用三角形的面积公式将面积关系转化为线段关系,再结合角的平分线的性质进一步转化为三角形的边长之间的关系,从而把两者建立起关系,结合已知条件可解决问题。
知识点拨
知识点1 作已知角的平分线
已知:∠AOB.
求作:∠AOB 的平分线.
作法:(1) 以点 O 为圆心,适当长为半径画弧,交 OA 于点 M,交 OB 于点 N;
(2) 分别以点 M、N 为圆心,大于MN 的长为半径画弧,两弧在∠AOB 的内部相交于点 C;
(3) 画射线 OC. 则射线 OC 即为所求.
【注意】(1)以小于MN 的长为半径画弧时,两弧没有交点.(2)不能说成“连接OC”.
【新知导学】
例1-1.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质( )
A. SAS B. ASA C. AAS D. SSS
【对应导练】
1.下列语句是有关几何作图的叙述.
①以O为圆心作弧;②延长射线AB到点C;③作∠AOB,使∠AOB=∠1;④作直线AB,使AB=a;⑤过三角形ABC的顶点C作它的对边AB的平行线.其中正确的有_____.(填序号即可)
2.已知:.
(1)尺规作图保留作图痕迹,不写作法:作的垂直平分线,使交于;
(2)连,若,,则的周长为______.
知识点2 角的平分线的性质
1、性质定理:角的平分线上的点到这个角的两边的距离相等.
2、应用所具备的条件:
(1)点在角的平分线上;
(2)到角两边的距离(垂直).
3、定理的作用:证明线段相等.
4、角平分线的性质的几何语言:
如图,∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PD=PE
【注意】①这里的距离是指点到角的两边垂线段的长;②该性质可以独立作为证明两条线段相等的依据,有时不必证明全等;③使用该结论的前提条件是图中有角平分线,有垂直.
【新知导学】
例2-1.如图,点D在的边上,且.
(1)作的平分线,交于点E(用尺规作图,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线与直线的位置关系,并说明理由.
【对应导练】
1.如图,,平分,交于C.
(1)尺规作图:过点B作的垂线,交于O,交于D,(保留作图痕迹,不写作法);
(2)求证:.
2.如图,中,点D在BC边上,,的平分线交AC于点E,过点E作,交BA的延长线于F,且,连接DE.
(1)求的度数;
(2)求证:DE平分;
(3)若,,,且,求的面积.
3.如图1,在中,,,AD,CE分别是,的平分线,AD,CE相交于点F.
(1)判断FE与FD之间的数量关系,并说明理由;
(2)如图2,如果不是直角,其他条件不变,(1)中所得结论是否仍然成立?请说明理由.
4.如图,已知BD是的平分线,,点P在BD上,,,垂足分别为M,N.试说明.
5.如图,中,平分,且,于E,于F,
(1)求证:与互补;
(2)如果,求的长.
题型训练
利用角平分线的作图在证明线段相等的应用
1.如图,四边形ABCD中,,,M为BC边上一点,且AM平分,DM平分.
求证:(1);
(2)M为BC的中点.
2.如图,已知BD是的平分线,,点P在BD上,,,垂足分别为M,N.试说明.
利用角平分线的性质求面积
3.如图,在中,的平分线相交于点O,连接OA,.求.
4.如图,在中,.
(1)过点B作的平分线交AC于点D(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);
(2)若,,求的面积.
利用角平分线的性质探究角的数量关系
5.如图13-1,已知BD是的角平分线,,交BD的延长线于点E.
(1)若.
①求和的度数
②求证:;
(2)如图13-2,AO平分,请直接写出与之间的数量关系.
6.如图,已知,AC平分,点B、D分别在AN、AM上.
(1)如图①,若,请你探索线段AD、AB、AC之间的数量关系,并给出证明;
(2)如图②,若,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
7.如图,,BD平分.求证:.
8.如图,在中,,为延长线上一点,,的平分线与交于点,连接.
(1)求证:点到的距离相等;
(2)求的度数.
牛刀小试
一、单选题(每小题4分,共32分)
1.下列尺规作图的语句错误的是( )
A. 作∠AOB,使∠AOB=∠α
B. 以点A为圆心,线段a的长为半径作弧
C. 作∠ABC,使∠ABC=∠α+∠β
D. 在∠AOC的边OC上用刻度尺截取5cm
2.如图,在Rt△ABC中,∠C=90°,以点A为圆心,适当长为半径作弧,分别交AB,AC于点D,E,再分别以点D,E,为圆心,以大于DE的长度为半径作弧,两弧交于点F,作射线AF交BC于点G,若AB=12,CG=3,则△ABG的面积是( )
A. 12 B. 18 C. 24 D. 36
3.如图,电信部门要修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路CD和EF的距离也必须相等.发射塔应该修建在( )
A. ∠AOB、∠COF两角的角平分线的交点
B. ∠COF的角平分线与线段AB的垂线平分线的交点
C. ∠DOF的角平分线与线段AB的垂线平分线的交点
D. ∠DOF、∠COF两角的角平分线分别与线段AB的垂线平分线的交点
4.如图,已知OC平分∠AOB,P是OC上任意一点,PD∥OA交OB于点D,PE⊥OA于点E,∠AOB=30°,如果PE=4,则OD的长为( )
A. 4 B. 6 C. 7 D. 8
5.如图,已知BP是∠ABC的平分线,AP⊥BP,若S△BPC=10cm2,则△ABC的面积等于( )
A. 20cm2 B. 30cm2 C. 25cm2 D. 不能确定
6.如图,在等边△ABC中,∠ABC和∠ACB的角平分线交于点D,过点D作EF//BC分别交AB、AC于点E、F,若EF=2,则△ABC的周长是( )
A. 10 B. 9 C. 8 D. 6
7.如图,AM垂直∠ABC的平分线BM于点M,D为BC中点,连接MD,若△ABC的面积为4,则△BMD的面积为( )
A. 1 B. 2 C. 2.5 D. 3
8.如图,点P为定角∠AOB平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论中,不正确的是( )
A. OM+ON的值不变 B. ∠PNM=∠POB
C. MN的长不变 D. 四边形PMON的面积不变
二、填空题(每小题4分,共20分)
9.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=20,则CD=_____.
10.如图,在Rt△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心,以小于AC长为半径作弧,分别交AC,AB于点M,N;②分别以M,N为圆心,以大于MN的长为半径作弧,在∠BAC内两弧交于点O;③作射线AO,交BC于点D.若点D到AB的距离为1,则CD的长为 _____.
11.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的是______.
①线段AD是△ABC的角平分线; ②∠ADC=60°;
③点D在AB的中垂线上; ④.
12.如图,在中,交于点,平分交于点,的面积为4,的面积为8,,则的长为 _____.
13.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,AB=6cm,则△DEB的周长为 _____.
三、解答题(共6小题,共48分)
14.(8分)如图,在△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,点F在BC上,连接DF,且AD=DF.
(Ⅰ)求证:CF=AE;
(Ⅱ)若AE=3,BF=4,求AB的长.
15.(8分)如图,△ABC 中,点D在边AC上,且AD=AB.
(1)请用无刻度的直尺和圆规作出∠A的平分线(保留作图痕迹,不写作法);
(2)若(1)中所作的角平分线与边BC交于点E,连接DE.求证:DE=BE.
16.(8分)如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=.
(1)尺规作图:作∠BAC的角平分线交BC于点P(不写作法,保留作图痕迹);
(2)在(1)所作图形中,求△ABP的面积.
17.(8分)如图,在中,为其角平分线,于点,于点,的面积是,,,求的长.
18.(8分)如图①,在△ABC中,AD是它的角平分线,P是AD上一点,PE∥AB交BC于E,PF∥AC交BC于F.
(1)求证:D到PE的距离与D到PF的距离相等;
(2)如图②,若点P在AD的延长线上,其他条件不变,试猜想(1)中的结论还成立吗?请证明你的猜想.
19 .(8分)在△ABC中,D是BC边上的点(不与点B、C重合),连接AD.
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD= ;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示);
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC= .
人教版八年级数学上名师点拨精练
第12章 全等三角形
12.3 角平分线的性质(1)
学习目标
1.通过全等三角形的知识理解角平分线的定理。
2.会利用尺规作一个角的角平分线。
3.在利用尺规作图的过程中培养学生的动手操作能力。
4.能运用角的平分线性质定理解决简单的几何问题。
【学习重难点】
角的平分线的性质的证明及运用。
老师告诉你
运用角的平分线的性质解决与面积有关问题的方法:
首先运用三角形的面积公式将面积关系转化为线段关系,再结合角的平分线的性质进一步转化为三角形的边长之间的关系,从而把两者建立起关系,结合已知条件可解决问题。
知识点拨
知识点1 作已知角的平分线
已知:∠AOB.
求作:∠AOB 的平分线.
作法:(1) 以点 O 为圆心,适当长为半径画弧,交 OA 于点 M,交 OB 于点 N;
(2) 分别以点 M、N 为圆心,大于MN 的长为半径画弧,两弧在∠AOB 的内部相交于点 C;
(3) 画射线 OC. 则射线 OC 即为所求.
【注意】(1)以小于MN 的长为半径画弧时,两弧没有交点.(2)不能说成“连接OC”.
【新知导学】
例1-1.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质( )
A. SAS B. ASA C. AAS D. SSS
【答案】D
【解析】利用作图的基本原理,得到线段的关系证明即可.
解:如图,由作图可知,BA=CF.
在△AOB和△CEF中,,
∴△AOB≌△CEF(SSS),
故选:D.
【对应导练】
1.下列语句是有关几何作图的叙述.
①以O为圆心作弧;②延长射线AB到点C;③作∠AOB,使∠AOB=∠1;④作直线AB,使AB=a;⑤过三角形ABC的顶点C作它的对边AB的平行线.其中正确的有_____.(填序号即可)
【答案】③⑤
【解析】①根据确定圆的两个条件:圆心和半径判断即可;
②根据射线的性质判断即可;
③根据基本作图:作一个角等于已知角判断即可;
④根据直线的性质判断即可;
⑤根据平行公理判断即可.
解:①以O为圆心作弧可以画出无数条弧,因为半径不固定,所以叙述错误;
②射线AB是由A向B向无限延伸,所以叙述错误;
③根据作一个角等于已知角的作法,可以作一个角∠AOB,使∠AOB等于已知∠1,所以叙述正确;
④直线可以向两方无限延伸,所以叙述错误;
⑤根据平行公理:过直线外一点有且只有一条直线与已知直线平行,可以过三角形ABC的顶点C作它的对边AB的平行线,所以叙述正确.
所以正确的有③⑤.
故答案为:③⑤.
2.已知:.
(1)尺规作图保留作图痕迹,不写作法:作的垂直平分线,使交于;
(2)连,若,,则的周长为______.
【答案】(1)见解析 (2)5
【解析】对于(1),分别以A、B两点为圆心,以大于长度为半径画弧,在两边分别相交于两点,然后过这两点作直线,即为的垂直平分线;
对于(2),根据线段垂直平分线的性质得出,再根据周长公式即可得出答案.
【小问1详解】
作图如图所示:
【小问2详解】
的垂直平分线,
.
,,
的周长是:(cm).
故答案为:.
【点睛】本题主要考查了尺规作图和线段垂直平分线的性质,解题的关键是掌握“垂直平分线上的点到这条线段两端点的距离相等”.
知识点2 角的平分线的性质
1、性质定理:角的平分线上的点到这个角的两边的距离相等.
2、应用所具备的条件:
(1)点在角的平分线上;
(2)到角两边的距离(垂直).
3、定理的作用:证明线段相等.
4、角平分线的性质的几何语言:
如图,∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PD=PE
【注意】①这里的距离是指点到角的两边垂线段的长;②该性质可以独立作为证明两条线段相等的依据,有时不必证明全等;③使用该结论的前提条件是图中有角平分线,有垂直.
【新知导学】
例2-1.如图,点D在的边上,且.
(1)作的平分线,交于点E(用尺规作图,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线与直线的位置关系,并说明理由.
答案:
解:(1)如图.
(2)理由如下:
平分
.
,
.
.
【对应导练】
1.如图,,平分,交于C.
(1)尺规作图:过点B作的垂线,交于O,交于D,(保留作图痕迹,不写作法);
(2)求证:.
答案:(1)解:如图为所作
(2)证明:,
平分,
,
,平分,
.
2.如图,中,点D在BC边上,,的平分线交AC于点E,过点E作,交BA的延长线于F,且,连接DE.
(1)求的度数;
(2)求证:DE平分;
(3)若,,,且,求的面积.
答案:(1)解:,,
.
,.
(2)证明:过点E作于G,于H,如图.
,,,
.
BE平分,,,
,.
,,DE平分.
(3)解:,
,即,解得,
,
的面积为.
3.如图1,在中,,,AD,CE分别是,的平分线,AD,CE相交于点F.
(1)判断FE与FD之间的数量关系,并说明理由;
(2)如图2,如果不是直角,其他条件不变,(1)中所得结论是否仍然成立?请说明理由.
答案:(1).理由如下:
过点F作于点M, 于点N,则,
,,
,的平分线AD,CE交于点F,
点F在的平分线上,
又,
(2)成立.理由如下:
过点F作于点M, 于点N,
则,,
,,
4.如图,已知BD是的平分线,,点P在BD上,,,垂足分别为M,N.试说明.
答案:BD平分,,
又,,
,.
又,,
.
5.如图,中,平分,且,于E,于F,
(1)求证:与互补;
(2)如果,求的长.
答案:(1)略 (2)
题型训练
利用角平分线的作图在证明线段相等的应用
1.如图,四边形ABCD中,,,M为BC边上一点,且AM平分,DM平分.
求证:(1);
(2)M为BC的中点.
答案:证明:(1),,
AM平分,DM平分,
,
,
,即.
(2)如图,过M作,垂足为点N,
,,
,,
AM平分,DM平分,
,,
,即M为BC的中点.
2.如图,已知BD是的平分线,,点P在BD上,,,垂足分别为M,N.试说明.
答案:BD平分,,
又,,
,.
又,,
.
利用角平分线的性质求面积
3.如图,在中,的平分线相交于点O,连接OA,.求.
答案:解:如图,过点O作,垂足分别为点D,E,F.
由三角形三条角平分线的性质定理,可知.
,
.
4.如图,在中,.
(1)过点B作的平分线交AC于点D(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);
(2)若,,求的面积.
答案:(1)图见解析
(2)的面积24
解析:(1)的平分线如图中BD所示.
(2)如图,过点D作于H.
平分,,,
,
的面积
.
利用角平分线的性质探究角的数量关系
5.如图13-1,已知BD是的角平分线,,交BD的延长线于点E.
(1)若.
①求和的度数
②求证:;
(2)如图13-2,AO平分,请直接写出与之间的数量关系.
答案:(1)①的度数为72°,的度数为18°;
②
由①可知
(2)
6.如图,已知,AC平分,点B、D分别在AN、AM上.
(1)如图①,若,请你探索线段AD、AB、AC之间的数量关系,并给出证明;
(2)如图②,若,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
答案:(1).
证明:AC平分,,
,
又,
,
则.
.
(2)仍然成立.
证明:如图,过点C分别作AM、AN的垂线,垂足分别为E、F,
AC平分,
(角平分线上的点到角两边的距离相等),
,,
,
又,
,
,,
由(1)可知,
.
7.如图,,BD平分.求证:.
答案:证明:过点D作BA、BC的垂线,垂足分别为E、F,则(角平分线上的点到这个角的两边的距离相等).
在和中,,
,
,
.
8.如图,在中,,为延长线上一点,,的平分线与交于点,连接.
(1)求证:点到的距离相等;
(2)求的度数.
答案:(1)如图,过点作于点于点,交的延长线于点,
平分,.
,,
,,
,点到的距离相等.
(2)由(1)知,平分.
平分.
.
牛刀小试
一、单选题(每小题4分,共32分)
1.下列尺规作图的语句错误的是( )
A. 作∠AOB,使∠AOB=∠α
B. 以点A为圆心,线段a的长为半径作弧
C. 作∠ABC,使∠ABC=∠α+∠β
D. 在∠AOC的边OC上用刻度尺截取5cm
【答案】C
【解析】根据基本作图的方法,逐项分析,从而得出结论.
解:A、作一个角等于已知角是常见的尺规作图,故不符合题意;
B、画弧既需要圆心,还需要半径,故不符合题意.
C、作一个角等于已知角,但不能等于两角的和,故符合题意;
D、在∠AOC的边OC上用刻度尺截取5cm,故不符合题意;
故选:C.
2.如图,在Rt△ABC中,∠C=90°,以点A为圆心,适当长为半径作弧,分别交AB,AC于点D,E,再分别以点D,E,为圆心,以大于DE的长度为半径作弧,两弧交于点F,作射线AF交BC于点G,若AB=12,CG=3,则△ABG的面积是( )
A. 12 B. 18 C. 24 D. 36
【答案】B
【解析】过点G作GH⊥AB于点H,根据题意得,AF是∠CAB的角平分线,得CG=GH,根据三角形面积公式,即可求出△ABG的面积.
解:过点G作GH⊥AB于点H,
根据题意得,AF是∠CAB的角平分线,
∵∠C=90°,
∴AC⊥CG,
∵GH⊥AB,
∴CG=GH,
∵CG=3,
∴,
故选:B.
3.如图,电信部门要修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路CD和EF的距离也必须相等.发射塔应该修建在( )
A. ∠AOB、∠COF两角的角平分线的交点
B. ∠COF的角平分线与线段AB的垂线平分线的交点
C. ∠DOF的角平分线与线段AB的垂线平分线的交点
D. ∠DOF、∠COF两角的角平分线分别与线段AB的垂线平分线的交点
【答案】B
【解析】由线段垂直平分线的性质可知:要两个城镇A,B的距离,发射塔必须建在线段AB的垂直平分线上,再根据角平分线的性质可知要到两条高速公路CD和EF的距离相等需要建在∠COF的平分线上,即可知发射塔要在两线的交点位置.
解:要两个城镇A,B的距离,发射塔必须建在线段AB的垂直平分线上,要到两条高速公路EF和CD的距离相等需要建在∠COF的平分线上,
∴发射塔应该修建在∠COF的平分线和线段AB的垂直平分线的交点处.
故选:B.
4.如图,已知OC平分∠AOB,P是OC上任意一点,PD∥OA交OB于点D,PE⊥OA于点E,∠AOB=30°,如果PE=4,则OD的长为( )
A. 4 B. 6 C. 7 D. 8
【答案】D
【解析】过P作PH⊥OB于H,由角平分线的性质得到PH=PE=4,由含30°角的直角三角形的性质得到PD=2PH=8,由平行线的性质,角平分线的定义推出∠DPO=∠DOP,因此OD=PD=8.
解:过P作PH⊥OB于H,
∵OC平分∠AOB,PE⊥AO,
∴PH=PE=4,
∵PD∥OA,
∴∠PDH=∠AOB=30°,
∴PD=2PH=8,
∵PD∥OA,
∴∠DPO=∠POE,
∵OC平分∠AOB,
∴∠DOP=∠POE,
∴∠DPO=∠DOP,
∴OD=PD=8.
故选:D.
5.如图,已知BP是∠ABC的平分线,AP⊥BP,若S△BPC=10cm2,则△ABC的面积等于( )
A. 20cm2 B. 30cm2 C. 25cm2 D. 不能确定
【答案】A
【解析】先延长AP交BC于点D,根据已知条件证明△BAP≌△BDP,从而证出AP=PD,根据等底同高面积相等,得到△APC的面积=△DPC的面积,最后根据△BPC的面积是12cm2,求出答案即可.
解:如图所示:延长AP交BC于点D,
∵BP是∠ABC的平分线,
∴∠ABP=∠DBP,
∵AP⊥BP,
∴∠APB=∠DPB=90°,
∵BP=BP,
∴△BAP≌△BDP(ASA),
∴AP=DP,
∴△APC的面积=△DPC的面积,
∵△BPC的面积=10(cm2),
∴△BPD的面积+△CPD的面积=10(cm2),
∴△ABP的面积+△APC的面积=10(cm2),
∴△ABC的面积=△BPD的面积+△CPD的面积+△ABP的面积+△APC的面积=20(cm2),
故选:A.
6.如图,在等边△ABC中,∠ABC和∠ACB的角平分线交于点D,过点D作EF//BC分别交AB、AC于点E、F,若EF=2,则△ABC的周长是( )
A. 10 B. 9 C. 8 D. 6
【答案】B
【解析】利用角平分线性质可得两组角相等,再结合平行线的性质,可证出∠OBE=∠EOB,∠OCF=∠COF,那么利用等角对等边可得线段的相等,再利用等量代换可求得EF=BE+CF.
解:∵BD、CD是∠ABC、∠ACB的角平分线,
∴∠DBE=∠DBC,∠DCF=∠BCD,
又∵EF∥BC,
∴∠DBC=∠BDE,∠BCD=∠CDF,
∴∠OBE=∠BOE,∠COF=∠OCF,
∴BE=DE,CF=DF,
∴EF=DE+DF=BE+CF=2,
∵△ABC是等边三角形,BE=1,
∴AB=BC=EF+BE=3,
∴△ABC的周长是9.
故选:B.
7.如图,AM垂直∠ABC的平分线BM于点M,D为BC中点,连接MD,若△ABC的面积为4,则△BMD的面积为( )
A. 1 B. 2 C. 2.5 D. 3
【答案】A
【解析】延长AM交BC于N,证明△AMB≌△NMB,根据全等三角形的性质得到AM=NM,根据三角形的面积公式计算即可.
解:延长AM交BC于N,
在△AMB和△NMB中,
,
∴△AMB≌△NMB(ASA),
∴AM=NM,
∴S△AMB=S△NMB,S△AMC=S△NMC,
∴S△BMC=S△ABC=2,
∵D为BC中点,
∴S△BMD=S△BMC=1,
故选:A.
8.如图,点P为定角∠AOB平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论中,不正确的是( )
A. OM+ON的值不变 B. ∠PNM=∠POB
C. MN的长不变 D. 四边形PMON的面积不变
【答案】C
【解析】过P作PL⊥OB于M,PQ⊥OA于N,可以证明△PMQ≌△PNL(AAS),得到PM=PN,MQ=LN,OQ=OL,因此OM+ON=MQ+OQ+OL-LN=2OQ=定值;设∠MPN=x°,
∠PNM=∠PON=90°-x°,由M、N在移动,得到MN的长在变化,四边形PMON的面积=四边形PQOL的面积=2×△POQ的面积=OQ PQ=定值.
解:过P作PL⊥OB于M,PQ⊥OA于N,
∵OP平分∠AOB,
∴PL=PQ,
∵∠MPN与∠AOB互补,
∴∠PMQ+∠PNO=180°,
∴∠PNL+∠PNO=180°,
∴∠PMQ=∠PNL,
∵∠PQM=∠PLN=90°,
∴△PMQ≌△PNL(AAS),
∴PM=PN,MQ=LN,OQ=OL,
∴OM+ON=MQ+OQ+OL-LN=2OQ,
∵∠AOB的度数是定值,OP的长是定值,
∴OQ的长是定值,
∴OM+ON的值不变,
故A不符合题意;
设∠MPN=x°,
∵PM=PN,
∴∠PNM=∠PMN=×(180°-x)=90°-x°,
∵∠AOB+∠MPN=180°,
∴∠AOB=180°-x°
∴∠PON=×(180°-x)=90°-x°,
∴∠PNM=∠PON,
故B不符合题意;
∵M、N在移动,
∴MN的长在变化,
故C符合题意;
∵△PMQ≌△PNL,
∴四边形PMON的面积=四边形PQOL的面积,
∵OP=OP,PQ=PL,
∴Rt△POQ≌Rt△POL(HL),
∴四边形PQOL的面积=2×△POQ的面积=OQ PQ,
∵OQ,PQ的长是定值,
∴四边形PMON的面积不变,
故D不符合题意.
故选:C.
二、填空题(每小题4分,共20分)
9.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=20,则CD=_____.
【答案】4
【解析】过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得DE=CD,然后利用△ABD的面积列式计算即可得解.
解:如图,过点D作DE⊥AB于点E;
∵∠C=90°,AD平分∠BAC,
∴CD=DE;
∵S△ABD=AB DE=×10 DE=20,
∴DE=4,
∴CD=DE=4.
故答案为:4.
10.如图,在Rt△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心,以小于AC长为半径作弧,分别交AC,AB于点M,N;②分别以M,N为圆心,以大于MN的长为半径作弧,在∠BAC内两弧交于点O;③作射线AO,交BC于点D.若点D到AB的距离为1,则CD的长为 _____.
【答案】1
【解析】根据角平分线的性质得到CD=点D到AB的距离=1.
解:由作图知AD平分∠BAC,
∵∠C=90°,点D到AB的距离为1,
∴CD=1.
故答案为:1.
11.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的是______.
①线段AD是△ABC的角平分线; ②∠ADC=60°;
③点D在AB的中垂线上; ④.
【答案】①②③④
【解析】先根据三角形内角和计算出∠BAC=60°,再利用基本作图对①进行判断;利用∠BAD=∠CAD=30°得到∠ADC=60°,则可对②进行判断;利用∠B=∠BAD得到DA=DB,根据线段垂直平分线的性质定理的逆定理可对③进行判断;利用30度角所对的直角边是斜边的一半、三角形的面积计算公式即可得出两个三角形的面积之比.
详解】解:由作法得,AD平分∠BAC,故①正确;
∵∠C=90°,∠B=30°,
∴∠BAC=60°,
∴,
∴,故②正确;
∵,
∴,
∴点D在AB的垂直平分线上,故③正确;
∵在直角△ACD中,∠CAD=30°,
∴,
∴,
,
∴,
∴,
∴.故④正确.
综上所述,正确的有①②③④.
故答案为:①②③④.
【点睛】本题考查了角平分线的性质、线段垂直平分线的性质以及作图-基本作图.解题时需要熟悉等腰三角形的判定与性质.
12.如图,在中,交于点,平分交于点,的面积为4,的面积为8,,则的长为 _____.
【答案】6
【解析】根据垂直的定义得到∠CHD=90°,根据三角形的面积求得DH=,过D作DE⊥BC于E,根据角平分线的性质得到DE=DH=,于是得到结论.
解:∵BH⊥AC,
∴∠CHD=90°,
∵△DCH的面积为4,CH=3,
∴DH=,
过D作DE⊥BC于E,
∵CD平分∠ACB交BH于点D
∴DE=DH=,
∵△BCD的面积为8,
∴DE BC=BC=8,
∴BC=6,
故答案为:6.
【点睛】本题考查了角平分线的性质,三角形的面积的计算,正确的作出辅助线是解题的关键.
13.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,AB=6cm,则△DEB的周长为 _____.
【答案】6cm
【解析】先利用角平分线的性质得到DC=DE,则△DEB的周长=BC+BE,再证明Rt△ACD≌Rt△AED得到AC=AE,所以△DEB的周长=AE+BE=AB.
解:∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴DC=DE,
∴△DEB的周长=DE+BE+BD=CD+BD+BE=BC+BE,
在Rt△ACD和Rt△AED中
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∵AC=BC,
∴AE=BC,
∴△DEB的周长=AE+BE=AB=6cm.
故答案为:6cm.
三、解答题(共6小题,共48分)
14.(8分)如图,在△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,点F在BC上,连接DF,且AD=DF.
(Ⅰ)求证:CF=AE;
(Ⅱ)若AE=3,BF=4,求AB的长.
【解析】(Ⅰ)通过HL证明Rt△CDF≌Rt△EDA,即可得出结论;
(Ⅱ)通过HL证明△BED≌△BCD,得BE=BC,再进行等量代换即可.
证明:(Ⅰ)∵∠C=90°,AD是∠BAC的平分线,DE⊥AB,
∴DE=DC,∠AED=90°,
在Rt△CDF与Rt△EDA中,
,
∴Rt△CDF≌Rt△EDA(HL),
∴CF=AE;
(Ⅱ)∵CF=AE,AE=3,
∴CF=3,
∵BF=4,
∴BC=BF+CF=4+3=7,
∵DE⊥AB,
∴∠DEB=90°,
∵∠C=90°,
∴∠DEB=∠C,
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD,
在△BED和△BCD中,
,
∴△BED≌△BCD(AAS),
∴BE=BC=7,
∴AB=BE+AE=7+3=10.
15.(8分)如图,△ABC 中,点D在边AC上,且AD=AB.
(1)请用无刻度的直尺和圆规作出∠A的平分线(保留作图痕迹,不写作法);
(2)若(1)中所作的角平分线与边BC交于点E,连接DE.求证:DE=BE.
【解析】(1)利用角平分线的作图步骤作图即可;
(2)证明△BAE≌△DAE(SAS),即可得出结论.
(1)解:如图所示,即为所求,
(2)证明:∵AE平分∠BAC,
∴∠BAE=∠DAE,
∵AB=AD,AE=AE,
∴△BAE≌△DAE(SAS),
∴DE=BE.
16.(8分)如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=.
(1)尺规作图:作∠BAC的角平分线交BC于点P(不写作法,保留作图痕迹);
(2)在(1)所作图形中,求△ABP的面积.
【解析】(1)根据角平分线的作法,即可画出图形;
(2)由勾股定理求出AC,由角平分线的性质得到PC=PD,根据三角形的面积公式求出PD,即可求出结论.
解:(1)如图所示:AP即为所求;
(2)在Rt△ABC中,∠ACB=90°,AB=5,BC=,
∴AC==2,
过点P作PD⊥AB于D,
∵AP是∠BAC的角平分线,
∴PD=PC,
∵△ABC的面积=△ACP的面积+△ABP的面积,
∴AC PC+AB PD=AC BC,
∴2PD+5PD=2,
解得PD=,
∴△ABP的面积=AB PD==.
17.(8分)如图,在中,为其角平分线,于点,于点,的面积是,,,求的长.
【答案】
【解析】根据角平分线上的点到角的两边距离相等可得,再根据,计算即可得解.
解:为的平分线,,,
,
∵,
∴,
即,
解得:,
.
【点睛】本题主要考查了角平分线上的点到角的两边距离相等的性质,三角形的面积,熟记性质并列出方程是解题的关键.
18.(8分)如图①,在△ABC中,AD是它的角平分线,P是AD上一点,PE∥AB交BC于E,PF∥AC交BC于F.
(1)求证:D到PE的距离与D到PF的距离相等;
(2)如图②,若点P在AD的延长线上,其他条件不变,试猜想(1)中的结论还成立吗?请证明你的猜想.
【分析】(1)首先由PE∥AB,PF∥AC,根据两直线平行,同位角相等,可得∠EPD=∠BAD,∠DPF=∠CAD,又由△ABC中,AD是它的角平分线,可得DP平分∠EPF,根据角平分线的性质,即可证得D到PE的距离与D到PF的距离相等;
(2)若点P在AD的延长线上,其他条件不变,(1)中的结论还成立,同(1)证明即可.
【解答】(1)证明:∵PE∥AB,PF∥AC,
∴∠EPD=∠BAD,∠DPF=∠CAD,
∵△ABC中,AD是它的角平分线,
∴∠BAD=∠CAD,
∴∠EPD=∠DPF,
即PD平分∠EPF,
∴D到PE的距离与D到PF的距离相等;
(2)若点P在AD的延长线上,其他条件不变,(1)中的结论还成立.理由如下:
∵PE∥AB,PF∥AC,
∴∠EPD=∠BAD,∠DPF=∠CAD,
∵△ABC中,AD是它的角平分线,
∴∠BAD=∠CAD,
∴∠EPD=∠DPF,
即PD平分∠EPF,
∴D到PE的距离与D到PF的距离相等.
【点评】此题考查了角平分线的性质与平行线的性质.此题难度不大,解题的关键是熟记角平分线的性质定理的应用,注意数形结合思想的应用.
19 .(8分)在△ABC中,D是BC边上的点(不与点B、C重合),连接AD.
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD= ;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示);
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC= .
【分析】(1)过A作AE⊥BC于E,根据三角形面积公式求出即可;
(2)过D作DE⊥AB于E,DF⊥AC于F,根据角平分线性质求出DE=DF,根据三角形面积公式求出即可;
(3)根据已知和(1)(2)的结论求出△ABD和△ACD的面积,即可求出答案.
【解答】解:(1)过A作AE⊥BC于E,
∵点D是BC边上的中点,
∴BD=DC,
∴SABD:S△ACD=(BD×AE):(CD×AE)=1:1,
故答案为:1:1;
(2)过D作DE⊥AB于E,DF⊥AC于F,
∵AD为∠BAC的角平分线,
∴DE=DF,
∵AB=m,AC=n,
∴SABD:S△ACD=(AB×DE):(AC×DF)=m:n;
(3)
∵AD=DE,
∴由(1)知:S△ABD:S△EBD=1:1,
∵S△BDE=6,
∴S△ABD=6,
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知:S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=3+6=9,
故答案为:9.
【点评】本题考查了角平分线性质和三角形的面积公式,能根据(1)(2)得出规律是解此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
