第1章 勾股定理检测卷-数学八年级上册北师大版(含解析)
文档属性
| 名称 | 第1章 勾股定理检测卷-数学八年级上册北师大版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-08 06:37:40 | ||
图片预览




文档简介
第1章勾股定理检测卷-数学八年级上册北师大版
一、单选题
1.已知一直角三角形两直角边的长分别为9,12,则它的斜边长为( )
A.15 B.16 C.17 D.25
2.中,,,,则的长为( )
A. B. C.或 D.或
3.如图,在中,,,,把沿折叠,使点C落在边的点E处,则的长为( )
A. B. C.3 D.5
4.如图,长方形中,,,将长方形折叠,使点与的中点重合,折痕为,则线段的长为( )
A. B.4 C. D.5
5.如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形的面积是100,小正方形的面积是4,直角三角形较长直角边为,较短直角边为,则的值是( )
A.10 B.12 C.14 D.16
6.如图由边长为正方形组成的的方格阵,点、、、都在格点上〔即行和列的交点处),、分别是、上的动点,则周长的最小值是( )
A. B. C. D.
7.如图,在中,是射线上的动点,,则当是直角三角形时,的长为( )
A. B. C. D.
8.在学习“勾股数”的知识时,爱思考的小琦发现了一组有规律的勾股数,并将它们记录在如下的表格中:
6 8 10 12 14
8 15 24 35 48
10 17 26 37 50
则当时,的值为( )
A.242 B.200 C.128 D.162
二、填空题
9.如图,为的角平分线,,若,,则的长为 .
10.如图,在中,,于点D,,则 .
11.如图所示,一棱长为的正方体,把所有的面均分成个小正方形.其边长都为假设一只蚂蚁每秒爬行,则它从上底面点沿表面爬行至侧面的点,最少要用 秒(结果保留一位小数).
12.如图,在一个由4×4个边长为1的小正方形组成的正方形网络,阴影部分面积是 .
13.我们知道,以3,4,5为边长的三角形是直角三角形,称3,4,5为勾股数组,记为,可以看作;同时8,6,10也为勾股数组,记为,可以看作.类似的,依次可以得到第三个勾股数组.请根据上述勾股数组规律,写出第5个勾股数组: .
14.如图,圆柱的底面周长是,圆柱高为,一只蚂蚁如果要沿着圆柱的表面从下底面点A爬到与之相对的上底面点B,那么它爬行的最短路程为 .
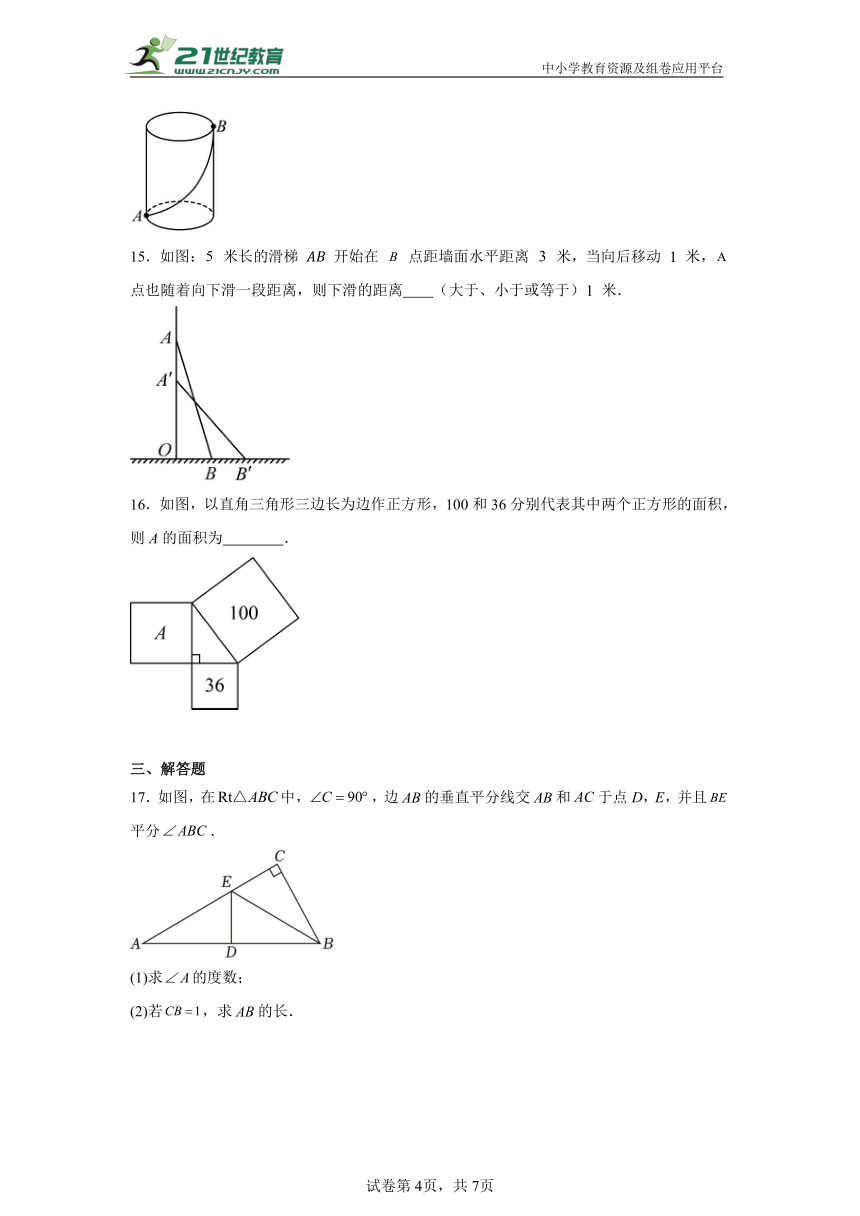
15.如图: 米长的滑梯 开始在 点距墙面水平距离 米,当向后移动 米, 点也随着向下滑一段距离,则下滑的距离 (大于、小于或等于) 米.
16.如图,以直角三角形三边长为边作正方形,100和36分别代表其中两个正方形的面积,则A的面积为 .
三、解答题
17.如图,在中,,边的垂直平分线交和于点D,E,并且平分.
(1)求的度数;
(2)若,求的长.
18.一艘轮船自西向东以每小时10海里的速度航行,上午.轮船在A处测得小岛C在北偏东方向上,到达B处,半径为15海里的范围内遍布暗礁,试问轮船继续向东航行是否有触礁的危险?请通过计算说明(参考数据:,)
19.如图,在笔直的公路旁有一座山,为方便运输货物现要从公路上的D处开道通一条公路到C处,已知点C与公路上的停靠站A的距离为,与公路上另一停靠站B的距离为,且.
(1)求修建的公路的长;
(2)若公路建成后,一辆货车由C处途经D处到达B处的总路程是多少?
20.如图,在,,,.点P从点A出发沿方向以的速度向终点B运动,点Q从点B出发沿方向以的速度向终点C运动,P,Q两点同时出发,设点P的运动时间为t秒.
(1)求的长;
(2)当时,求P,Q两点之间的距离;
(3)当时,求t的值?
21.(1)【基础巩固】
如图1,在和中,点D在线段上,,.线段与的数量关系为 ,位置关系为 ;
(2)【变式训练】
如图2,当点D在线段的延长线上,其它条件不变,(1)中的结论是否仍然成立,请说明理由.
(3)【拓展提高】
如图3,在和中,点D在线段上,如果,,,.求的值.
中小学教育资源及组卷应用平台
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8
答案 A A B B C B C D
1.A
【分析】本题考查了勾股定理,运用直角三角形的斜边平方等于两直角边平方和,代入数值进行计算,即可作答.
【详解】解:∵一直角三角形两直角边的长分别为9,12
∴斜边长为
故选:A
2.A
【分析】本题考查了勾股定理,根据勾股定理求解即可.
【详解】中,,,,
,
故选:A.
3.B
【分析】本题主要考查了勾股定理,折叠的性质,先根据勾股定理得出,然后求出,设,则,根据勾股定理得出,解方程即可.
【详解】解:∵在中,,,,
∴,
根据折叠可知:,,
∴,
设,则,
根据勾股定理得:,
∴,
解得:,
∴,
故选:B.
4.B
【分析】设,则,根据长方形,,得到,根据勾股定理,得,解得,解答即可.
本题考查了长方形的性质,折叠的性质,勾股定理,熟练掌握折叠的性质,勾股定理是解题的关键.
【详解】解:设,则,
∵长方形,,点与的中点重合,
∴,,
根据折叠的性质,得
∴,
解得,
故选B.
5.C
【分析】根据正方形的面积及直角边的关系,列出方程组,然后求解.本题考查勾股定理的证明,关键是根据正方形、直角三角形的性质及分析问题解答.
【详解】解:由条件可得,
即,,
则,
所以(负值已舍去),
故选:C.
6.B
【分析】本题考查了轴对称的性质、勾股定理,分别作点关于、的对称点、,连接交于,交于,由轴对称的性质得出周长的最小值,再由勾股定理计算即可得出答案.
【详解】解:如图,分别作点关于、的对称点、,连接交于,交于,
,
则,,
∵周长,
∴周长的最小值
∴周长的最小值为,
故选:B.
7.C
【分析】本题主要考查了勾股定理,等边三角形的判定及性质,含直角三角形的性质和直角三角形斜边的中线,分类讨论,数形结合是解答此题的关键.
【详解】解:当时,
;
在中,,
当,
,
,
,
,
为等边三角形,
,
,
;
情况二:
,
,
,
为等边三角形,
;
故选C.
8.D
【分析】本题考查了勾股数,关键是注意观察表格中的数据,确定、、的数量关系.
根据表格中数据确定、、的关系,然后再代入求出、的值进而可得答案.
【详解】解:根据表格中数据可得:,并且,
则,
当时,,
解得,
则,
则.
故选:D.
9.
【分析】本题考查了全等三角形的判定与性质,勾股定理,等面积法,正确掌握相关性质内容是解题的关键.先分别过作,在上截取,证明,经过等面积法得,结合勾股定理,,运用 数值计算,即可作答.
【详解】解:如图:分别过作,在上截取
∵为的角平分线
∴
∵,
∴
则
∵
∴
∵,
∴
∴
过点H作
∴
∴
则
∵
∴
∴
则
∵
∴
∴
在
∴
∴
解得(负值已舍去)
故答案为:
10.6
【分析】本题主要考查了勾股定理,先求出,再利用勾股定理可得.
【详解】解:∵,
∴,
∵,
∴,
在中,由勾股定理得,
故答案为:6.
11.
【分析】本题考查了勾股定理的拓展应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.把此正方体的点所在的面展开,然后在平面内,利用勾股定理求点和点间的线段长,即可得到蚂蚁爬行的最短距离.
【详解】解:如下图所示,将正方体沿着它的棱长展开,由勾股定理得;
如下图所示,将正方体沿着它的棱长展开,由勾股定理得;
如下图所示,将正方体沿着它的棱长展开,由勾股定理得,
∵
∴最短路径长为,
∴用时最少为秒.
故答案为:.
12.
【分析】此题考查了勾股定理及正方形的面积的计算.结合网格图,利用勾股定理求正方形边长是解此题的关键.先利用勾股定理计算得长,再利用正方形面积公式即可求得答案.
【详解】∵为直角三角形,由勾股定理得:
,
故易知阴影为正方形,
故
故答案为:
13.
【分析】本题考查数字型规律探究、勾股数,能从数字等式中找到变化规律是解答的关键.
根据给出的3组数以及勾股数的定义即可得出答案.
【详解】解:上述四组勾股数组的规律是:,
即,
∴
所以第5个勾股数组为,
故答案为:.
14./13厘米
【分析】本题考查勾股定理的应用—最短路径问题,将圆柱体展开,利用勾股定理求出最短路径的长即可.
【详解】解:把圆柱沿母线展开,点B展开后的对应点为,利用两点之间线段最短可判断蚂蚁爬行的最短路径为,如图所示:
由题意,得:,
在中,由勾股定理,得:;
故答案为:.
15.等于
【分析】本题主要考查勾股定理的应用,勾股定理:两直角边的平方和等于斜边的平方.
直接利用勾股定理得出的长,进而求出的长,即可得出答案.
【详解】解:由题意可得:,
故,
∵当向后移动 1 米,
,
,
则.
故下滑的距离为 1 米,
故答案为:等于.
16.64
【分析】本题考查了正方形各边相等,各内角为直角的性质,考查了直角三角形中勾股定理的运用,根据两个正方形的面积计算正方形的边长,计算的边长即为直角三角形的直角边和斜边,根据勾股定理可以计算直角边,即正方形A的边长.
【详解】解:因为以两个边长的正方形面积为100和36,则边长为和,
所以直角边的平方,
∴A的面积为64,
故答案为:64.
17.(1)
(2)2
【分析】此题考查了垂直平分线的性质,三角形内角和定理,勾股定理和含30度角直角三角形的性质,解题的关键是熟练掌握以上知识点.
(1)根据垂直平分线的性质得到,进而得到.由角平分线的概念得到,进而利用三角形内角和定理求解即可;
(2)根据含30度角直角三角形的性质得到,进而求解即可.
【详解】(1)解:∵边的垂直平分线交和于点D,E,
∴,
∴.
又∵平分,
∴,
而,
又∵,
∴.
(2)解:∵,
∴,
∵,
∴.
18.轮船继续向东航行没有触礁的危险
【分析】本题考查了勾股定理的实际应用,解题的关键是正确作出辅助线,构造直角三角形.
过点C作于点D,,海里,推出,则海里,再得出,则海里,根据勾股定理可得:(海里),即可得出结论.
【详解】解:过点C作于点D,
由题意可知,,海里,
∴,
∴,
∴海里,
∵,
∴,
∴海里,
根据勾股定理可得:(海里),
∵,
∴轮船继续向东航行没有触礁的危险.
19.(1)修建的公路的长为
(2)一辆货车由C处途经D处到达B处的总路程为
【分析】本题考查了勾股定理的实际应用,解题的关键是掌握直角三角形两直角边平方和等于斜边平方.
(1)先根据勾股定理得出,再根据列出方程计算即可;
(2)先根据勾股定理求出,即可解答.
【详解】(1)解:∵,
∴根据勾股定理可得:,
∵,
∴,即,
∴,
解得:,
∴修建的公路的长为.
(2)解:∵,
∴根据勾股定理可得:,
∴
答:一辆货车由C处途经D处到达B处的总路程为.
20.(1)
(2)
(3)、两点运动秒,.
【分析】(1)在中,根据勾股定理来求的长度;
(2)在中,根据勾股定理来求的长度;
(3)由路程时间速度求出,,再根据等量关系:列出方程求解即可.
本题考查了勾股定理和一元一次方程的应用.解题时,需要熟悉路程时间速度,以及变形后的公式.
【详解】(1)解:在中,,,,
.
(2)解:如图,连接,,
,
,
在中,由勾股定理得到:;
(3)解:设秒后,,,
∵,
∴,
解得.
答:、两点运动秒,.
21.(1) (2)仍成立;理由见解析 (3)128
【分析】本题考查了全等三角形的性质与判定,等腰直角三角形的性质,勾股定理等,掌握全等三角形的性质与判定是解题的关键.
(1)根据证明,得出,从而得到;
(2)根据证明,得出,从而得到;
(3)由勾股定理得,过点A作,交于点F,证明得,求出,由勾股定理求出,进而可求出的值.
【详解】(1)∵,
∴,
∴,
又∵,
∴,
∴,.
∵,
∴,
∴,
∴,
即;
故答案为:;
(2)当点D在的延长线上时,(1)的结论仍成立.
∵,
∴,
∴,
又∵,
∴,
∴,.
∵,
∴,
∴,
∴,
即;
(3)在中,,
∴
过点A作,交于点F,
∴
∴
∵在中,
∴
∴
又∵,
∴,
∴
∴
在中,
∴
∴
∴
∴
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知一直角三角形两直角边的长分别为9,12,则它的斜边长为( )
A.15 B.16 C.17 D.25
2.中,,,,则的长为( )
A. B. C.或 D.或
3.如图,在中,,,,把沿折叠,使点C落在边的点E处,则的长为( )
A. B. C.3 D.5
4.如图,长方形中,,,将长方形折叠,使点与的中点重合,折痕为,则线段的长为( )
A. B.4 C. D.5
5.如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形的面积是100,小正方形的面积是4,直角三角形较长直角边为,较短直角边为,则的值是( )
A.10 B.12 C.14 D.16
6.如图由边长为正方形组成的的方格阵,点、、、都在格点上〔即行和列的交点处),、分别是、上的动点,则周长的最小值是( )
A. B. C. D.
7.如图,在中,是射线上的动点,,则当是直角三角形时,的长为( )
A. B. C. D.
8.在学习“勾股数”的知识时,爱思考的小琦发现了一组有规律的勾股数,并将它们记录在如下的表格中:
6 8 10 12 14
8 15 24 35 48
10 17 26 37 50
则当时,的值为( )
A.242 B.200 C.128 D.162
二、填空题
9.如图,为的角平分线,,若,,则的长为 .
10.如图,在中,,于点D,,则 .
11.如图所示,一棱长为的正方体,把所有的面均分成个小正方形.其边长都为假设一只蚂蚁每秒爬行,则它从上底面点沿表面爬行至侧面的点,最少要用 秒(结果保留一位小数).
12.如图,在一个由4×4个边长为1的小正方形组成的正方形网络,阴影部分面积是 .
13.我们知道,以3,4,5为边长的三角形是直角三角形,称3,4,5为勾股数组,记为,可以看作;同时8,6,10也为勾股数组,记为,可以看作.类似的,依次可以得到第三个勾股数组.请根据上述勾股数组规律,写出第5个勾股数组: .
14.如图,圆柱的底面周长是,圆柱高为,一只蚂蚁如果要沿着圆柱的表面从下底面点A爬到与之相对的上底面点B,那么它爬行的最短路程为 .
15.如图: 米长的滑梯 开始在 点距墙面水平距离 米,当向后移动 米, 点也随着向下滑一段距离,则下滑的距离 (大于、小于或等于) 米.
16.如图,以直角三角形三边长为边作正方形,100和36分别代表其中两个正方形的面积,则A的面积为 .
三、解答题
17.如图,在中,,边的垂直平分线交和于点D,E,并且平分.
(1)求的度数;
(2)若,求的长.
18.一艘轮船自西向东以每小时10海里的速度航行,上午.轮船在A处测得小岛C在北偏东方向上,到达B处,半径为15海里的范围内遍布暗礁,试问轮船继续向东航行是否有触礁的危险?请通过计算说明(参考数据:,)
19.如图,在笔直的公路旁有一座山,为方便运输货物现要从公路上的D处开道通一条公路到C处,已知点C与公路上的停靠站A的距离为,与公路上另一停靠站B的距离为,且.
(1)求修建的公路的长;
(2)若公路建成后,一辆货车由C处途经D处到达B处的总路程是多少?
20.如图,在,,,.点P从点A出发沿方向以的速度向终点B运动,点Q从点B出发沿方向以的速度向终点C运动,P,Q两点同时出发,设点P的运动时间为t秒.
(1)求的长;
(2)当时,求P,Q两点之间的距离;
(3)当时,求t的值?
21.(1)【基础巩固】
如图1,在和中,点D在线段上,,.线段与的数量关系为 ,位置关系为 ;
(2)【变式训练】
如图2,当点D在线段的延长线上,其它条件不变,(1)中的结论是否仍然成立,请说明理由.
(3)【拓展提高】
如图3,在和中,点D在线段上,如果,,,.求的值.
中小学教育资源及组卷应用平台
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8
答案 A A B B C B C D
1.A
【分析】本题考查了勾股定理,运用直角三角形的斜边平方等于两直角边平方和,代入数值进行计算,即可作答.
【详解】解:∵一直角三角形两直角边的长分别为9,12
∴斜边长为
故选:A
2.A
【分析】本题考查了勾股定理,根据勾股定理求解即可.
【详解】中,,,,
,
故选:A.
3.B
【分析】本题主要考查了勾股定理,折叠的性质,先根据勾股定理得出,然后求出,设,则,根据勾股定理得出,解方程即可.
【详解】解:∵在中,,,,
∴,
根据折叠可知:,,
∴,
设,则,
根据勾股定理得:,
∴,
解得:,
∴,
故选:B.
4.B
【分析】设,则,根据长方形,,得到,根据勾股定理,得,解得,解答即可.
本题考查了长方形的性质,折叠的性质,勾股定理,熟练掌握折叠的性质,勾股定理是解题的关键.
【详解】解:设,则,
∵长方形,,点与的中点重合,
∴,,
根据折叠的性质,得
∴,
解得,
故选B.
5.C
【分析】根据正方形的面积及直角边的关系,列出方程组,然后求解.本题考查勾股定理的证明,关键是根据正方形、直角三角形的性质及分析问题解答.
【详解】解:由条件可得,
即,,
则,
所以(负值已舍去),
故选:C.
6.B
【分析】本题考查了轴对称的性质、勾股定理,分别作点关于、的对称点、,连接交于,交于,由轴对称的性质得出周长的最小值,再由勾股定理计算即可得出答案.
【详解】解:如图,分别作点关于、的对称点、,连接交于,交于,
,
则,,
∵周长,
∴周长的最小值
∴周长的最小值为,
故选:B.
7.C
【分析】本题主要考查了勾股定理,等边三角形的判定及性质,含直角三角形的性质和直角三角形斜边的中线,分类讨论,数形结合是解答此题的关键.
【详解】解:当时,
;
在中,,
当,
,
,
,
,
为等边三角形,
,
,
;
情况二:
,
,
,
为等边三角形,
;
故选C.
8.D
【分析】本题考查了勾股数,关键是注意观察表格中的数据,确定、、的数量关系.
根据表格中数据确定、、的关系,然后再代入求出、的值进而可得答案.
【详解】解:根据表格中数据可得:,并且,
则,
当时,,
解得,
则,
则.
故选:D.
9.
【分析】本题考查了全等三角形的判定与性质,勾股定理,等面积法,正确掌握相关性质内容是解题的关键.先分别过作,在上截取,证明,经过等面积法得,结合勾股定理,,运用 数值计算,即可作答.
【详解】解:如图:分别过作,在上截取
∵为的角平分线
∴
∵,
∴
则
∵
∴
∵,
∴
∴
过点H作
∴
∴
则
∵
∴
∴
则
∵
∴
∴
在
∴
∴
解得(负值已舍去)
故答案为:
10.6
【分析】本题主要考查了勾股定理,先求出,再利用勾股定理可得.
【详解】解:∵,
∴,
∵,
∴,
在中,由勾股定理得,
故答案为:6.
11.
【分析】本题考查了勾股定理的拓展应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.把此正方体的点所在的面展开,然后在平面内,利用勾股定理求点和点间的线段长,即可得到蚂蚁爬行的最短距离.
【详解】解:如下图所示,将正方体沿着它的棱长展开,由勾股定理得;
如下图所示,将正方体沿着它的棱长展开,由勾股定理得;
如下图所示,将正方体沿着它的棱长展开,由勾股定理得,
∵
∴最短路径长为,
∴用时最少为秒.
故答案为:.
12.
【分析】此题考查了勾股定理及正方形的面积的计算.结合网格图,利用勾股定理求正方形边长是解此题的关键.先利用勾股定理计算得长,再利用正方形面积公式即可求得答案.
【详解】∵为直角三角形,由勾股定理得:
,
故易知阴影为正方形,
故
故答案为:
13.
【分析】本题考查数字型规律探究、勾股数,能从数字等式中找到变化规律是解答的关键.
根据给出的3组数以及勾股数的定义即可得出答案.
【详解】解:上述四组勾股数组的规律是:,
即,
∴
所以第5个勾股数组为,
故答案为:.
14./13厘米
【分析】本题考查勾股定理的应用—最短路径问题,将圆柱体展开,利用勾股定理求出最短路径的长即可.
【详解】解:把圆柱沿母线展开,点B展开后的对应点为,利用两点之间线段最短可判断蚂蚁爬行的最短路径为,如图所示:
由题意,得:,
在中,由勾股定理,得:;
故答案为:.
15.等于
【分析】本题主要考查勾股定理的应用,勾股定理:两直角边的平方和等于斜边的平方.
直接利用勾股定理得出的长,进而求出的长,即可得出答案.
【详解】解:由题意可得:,
故,
∵当向后移动 1 米,
,
,
则.
故下滑的距离为 1 米,
故答案为:等于.
16.64
【分析】本题考查了正方形各边相等,各内角为直角的性质,考查了直角三角形中勾股定理的运用,根据两个正方形的面积计算正方形的边长,计算的边长即为直角三角形的直角边和斜边,根据勾股定理可以计算直角边,即正方形A的边长.
【详解】解:因为以两个边长的正方形面积为100和36,则边长为和,
所以直角边的平方,
∴A的面积为64,
故答案为:64.
17.(1)
(2)2
【分析】此题考查了垂直平分线的性质,三角形内角和定理,勾股定理和含30度角直角三角形的性质,解题的关键是熟练掌握以上知识点.
(1)根据垂直平分线的性质得到,进而得到.由角平分线的概念得到,进而利用三角形内角和定理求解即可;
(2)根据含30度角直角三角形的性质得到,进而求解即可.
【详解】(1)解:∵边的垂直平分线交和于点D,E,
∴,
∴.
又∵平分,
∴,
而,
又∵,
∴.
(2)解:∵,
∴,
∵,
∴.
18.轮船继续向东航行没有触礁的危险
【分析】本题考查了勾股定理的实际应用,解题的关键是正确作出辅助线,构造直角三角形.
过点C作于点D,,海里,推出,则海里,再得出,则海里,根据勾股定理可得:(海里),即可得出结论.
【详解】解:过点C作于点D,
由题意可知,,海里,
∴,
∴,
∴海里,
∵,
∴,
∴海里,
根据勾股定理可得:(海里),
∵,
∴轮船继续向东航行没有触礁的危险.
19.(1)修建的公路的长为
(2)一辆货车由C处途经D处到达B处的总路程为
【分析】本题考查了勾股定理的实际应用,解题的关键是掌握直角三角形两直角边平方和等于斜边平方.
(1)先根据勾股定理得出,再根据列出方程计算即可;
(2)先根据勾股定理求出,即可解答.
【详解】(1)解:∵,
∴根据勾股定理可得:,
∵,
∴,即,
∴,
解得:,
∴修建的公路的长为.
(2)解:∵,
∴根据勾股定理可得:,
∴
答:一辆货车由C处途经D处到达B处的总路程为.
20.(1)
(2)
(3)、两点运动秒,.
【分析】(1)在中,根据勾股定理来求的长度;
(2)在中,根据勾股定理来求的长度;
(3)由路程时间速度求出,,再根据等量关系:列出方程求解即可.
本题考查了勾股定理和一元一次方程的应用.解题时,需要熟悉路程时间速度,以及变形后的公式.
【详解】(1)解:在中,,,,
.
(2)解:如图,连接,,
,
,
在中,由勾股定理得到:;
(3)解:设秒后,,,
∵,
∴,
解得.
答:、两点运动秒,.
21.(1) (2)仍成立;理由见解析 (3)128
【分析】本题考查了全等三角形的性质与判定,等腰直角三角形的性质,勾股定理等,掌握全等三角形的性质与判定是解题的关键.
(1)根据证明,得出,从而得到;
(2)根据证明,得出,从而得到;
(3)由勾股定理得,过点A作,交于点F,证明得,求出,由勾股定理求出,进而可求出的值.
【详解】(1)∵,
∴,
∴,
又∵,
∴,
∴,.
∵,
∴,
∴,
∴,
即;
故答案为:;
(2)当点D在的延长线上时,(1)的结论仍成立.
∵,
∴,
∴,
又∵,
∴,
∴,.
∵,
∴,
∴,
∴,
即;
(3)在中,,
∴
过点A作,交于点F,
∴
∴
∵在中,
∴
∴
又∵,
∴,
∴
∴
在中,
∴
∴
∴
∴
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
