第1章 一元二次方程检测卷-数学九年级上册苏科版(含解析)
文档属性
| 名称 | 第1章 一元二次方程检测卷-数学九年级上册苏科版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 564.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-08 06:36:19 | ||
图片预览




文档简介
第1章一元二次方程检测卷-数学九年级上册苏科版
一、单选题
1.下列方程是一元二次方程的是( )
A. B. C. D.
2.方程的根是( )
A. B. C. D.或
3.方程二次项系数,一次项系数和常数项分别是( )
A.1,,1 B.,,1 C.1,3, D.1,3,1
4.如果是方程的一个根,则的值为( )
A.3 B.2 C. D.
5.已知实数a,b满足,则的值为( )
A.3 B.5 C.或5 D.3或
6.在平面直角坐标系中,若直线不经过第四象限,则关于x的方程的实数根的情况为( )
A.无解 B.两个不相等的实数根
C.两个相等的实数根 D.无法确定
7.如图是由一些等边三角形“△”堆成的“金字塔”图形,它的下一排依次比上一排多一个“△”;若第个图形的“△”的个数为45个,则的值为( )
A.7 B.8 C.9 D.10
8.某校截止到2022年底,校园绿化面积为1000平方米.为美化环境,该校计划2024年底绿化面积达到1440平方米.利用方程想想,设这两年绿化面积的年平均增长率为,则依题意列方程为( )
A. B.
C. D.
二、填空题
9.已知,,,求 .
10.小华在解一元二次方程时,只得出一个根是,则被他漏掉的一个根是 .
11.若a为方程的解,则的值为 .
12.美术兴趣小组在中秋节这一天人人相互送一个月饼,共送出56个月饼,美术兴趣小组人数是 .
13.若实数p、q,满足,,且,则的值为 .
14.已知,是方程的两个根,则代数式的值为 .
15.某产品原来成本是25元,按照固定的百分率降低成本,连续两次降低后比一次降低后所剩的成本少4元,设这个百分率为x,可得方程 .
16.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留宽的门.已知计划中的材料可建墙体(不包括门)总长为,则当建成的饲养室总占地面积为时,垂直于墙的一边长为 .
三、解答题
17.解方程∶
(1)
(2)
18.已知关于的一元二次方程.求证:无论取任何实数,此方程总有实数根.
19.已知关于x的方程.
(1)求证:方程总有两个实数根;
(2)若方程有一个不小于 3的根,求实数k的取值范围.
20.物美商场于今年年初以每件元的进价购进一批商品.当商品售价为元时,一月份销售件.二、三月该商品十分畅销.销售量持续走高.在售价不变的基础上,三月底的销售量达到件.设二、三这两个月销售量的月平均增长率不变.
(1)求二、三这两个月销售量的月平均增长率.
(2)从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每降价元,销售量增加件,当商品降价多少元时,商场获利元?
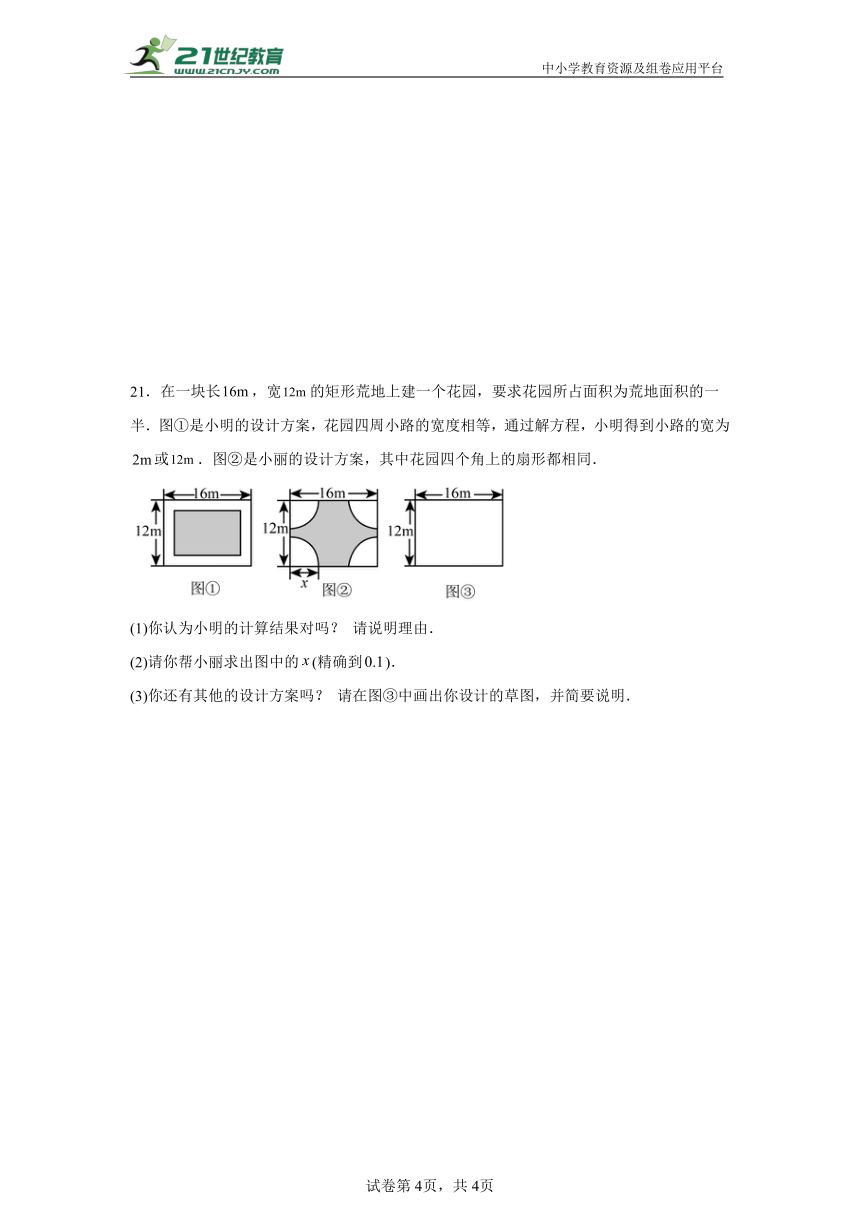
21.在一块长,宽的矩形荒地上建一个花园,要求花园所占面积为荒地面积的一半.图①是小明的设计方案,花园四周小路的宽度相等,通过解方程,小明得到小路的宽为或.图②是小丽的设计方案,其中花园四个角上的扇形都相同.
(1)你认为小明的计算结果对吗? 请说明理由.
(2)请你帮小丽求出图中的(精确到).
(3)你还有其他的设计方案吗? 请在图③中画出你设计的草图,并简要说明.
中小学教育资源及组卷应用平台
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8
答案 A D A C B B C B
1.A
【分析】本题考查了一元二次方程的概念,根据一元二次方程的定义,必须满足四个条件:①未知数的最高次数是2;②二次项系数不为0;③是整式方程;④含有一个未知数.由这四个条件对四个选项进行验证,满足这四个条件者为正确答案.
【详解】解:.是一元二次方程,该选项正确,符合题意;
. 是二元二次方程,该选项错误,不符合题意;
. 不是一元二次方程,该选项错误,不符合题意;
. 不是一元二次方程,该选项错误,不符合题意;
故选:A.
2.D
【分析】本题考查了解一元二次方程,掌握因式分解是解题的关键,根据题意,移项,再提取公因式即可求解.
【详解】解:
移项得,
提取公因式得,,整理得,,
解得,,,
故选:D .
3.A
【分析】本题主要考查了一元二次方程的一般式,对于一元二次方程,其中a、b、c是常数且,a叫做二次项系数,b叫做一次项系数,c叫做常数项,据此可得答案.
【详解】解:把原方程化为一般式为,
∴原方程的二次项系数为1,一次项系数为,常数项为1,
故选:A.
4.C
【分析】本题主要考查了一元二次方程的解,将代入方程,求解即可.
【详解】解:根据题意得:,
,
故选:C.
5.B
【分析】本题主要考查了换元法解一元二次方程,设,则原方程变为,解这个方程即可求得的值.
【详解】解:设,
原方程变为:,
,
解得:,
因为平方和是非负数,
所以的值为5;
故选:B.
6.B
【分析】本题考查了一次函数的性质,根的判别式:一元二次方程的根与有如下关系:当时,方程有两个不相等的实数根;当时,方程有两个相等的实数根;当时,方程无实数根.由直线解析式求得,然后确定的符号即可.
【详解】解:直线不经过第四象限,
,
关于的方程,
,
关于的方程有两个不相等的实数根.
故选:B.
7.C
【分析】此题考查了图形变化类规律问题的解决能力,解一元二次方程,关键是能根据观察图形变化,能够猜想、验证、归纳出此题规律,并能运用此规律解决相关问题.找出规律,第个图形有个“△”,再解一元二次方程即可.
【详解】解:第1个图形有1个,
第2个图形有个,
第3个图形有个,
第4个图形有个,
,
则第个图形有个,
∴,
解得:或(舍),
故选:C.
8.B
【分析】本题考查了一元二次方程的应用,设这两年绿化面积的年平均增长率为,根据“某校截止到2022年底,校园绿化面积为1000平方米.为美化环境,该校计划2024年底绿化面积达到1440平方米”列出方程即可,理解题意,找准等量关系,正确列出方程是解此题的关键.
【详解】解:设这两年绿化面积的年平均增长率为,则依题意列方程为,
故选:B.
9.2
【分析】本题主要考查一元二次方程根与系数的关系,a,b可以看作是一元二次方程的两根,根据根与系数的关系求解即可.
【详解】解:∵,,
∴a,b可以看作是一元二次方程的两根,
∴
故答案为:2.
10.
【分析】本题考查的是一元二次方程的解法,直接利用因式分解的方法解方程即可得到答案.
【详解】解:∵,
∴,
∴或,
解得:,,
∴被他漏掉的一个根是;
故答案为:
11.7
【分析】本题考查了一元二次方程的解,代数式求值,熟练掌握一元二次方程的解与一元二次方程的关系是解题的关键.
由题意得,将其变形与进行关联,即可求解.
【详解】解:∵a为方程的解,
∴,
∴,
∴.
故答案为:7.
12.8
【分析】本题主要考查一元二次方程的应用,找准等量关系列出方程是解题的关键.
根据题意找到“小组的人数(小组人数)”,然后列式计算即可.
【详解】解:设美术兴趣小组有x人,
,
解得:,(负值舍去),
∴美术兴趣小组有8人.
故答案为:8.
13.
【分析】本题考查一元二次方程根的定义,根与系数的关系,完全平方公式及其变式,由已知和是一元二次方程的两根,再根据一元二次方程根与系数的关系求出和的值,再利用完全平方公式的变式即可解决问题,灵活运用一元二次方程根的定义和根的判别式是解题的关键.
【详解】解:∵若实数p、q,满足,,
∴和是一元二次方程,即的两根,
∴,即,
∴,
∵,
∴,
∴,
故答案为:.
14.
【分析】本题考查了根与系数的关系,整式的混合运算,解题的关键是牢记两根之和等于、两根之积等于.
根据先将整式化简,,是方程的两个根,求得,,代入即可求解;
【详解】解: ,是方程的两个根,
,,
将,代入
可得:
故答案为:
15.
【分析】本题主要考查了一元二次方程的应用,解题的关键是设降低的百分率为x,再表示出连续两次降低后的成本,一次降低后的成本,根据连续两次降低后比一次降低后所剩的成本少4元,列出方程即可.
【详解】解:设降低的百分率为x,根据题意得:
.
故答案为:.
16.5
【分析】本题主要考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
设垂直于墙的材料长为米,则平行于墙的材料长为,表示出总面积:,由此列出方程并求得的值即可.
【详解】解:设垂直于墙的材料长为,则平行于墙的材料长为,
根据题意,得.
解得:,
故答案为:5.
17.(1)
(2)
【分析】本题主要考查了解一元二次方程:
(1)利用配方法解方程即可;
(2)先移项,然后利用因式分解法解方程即可.
【详解】(1)解:∵,
∴,
∴,
∴,
解得;
(2)解:∵,
∴,
∴,
∴或,
解得.
18.见解析
【分析】本题考查一元二次方程根的判别式,解题的关键是掌握根的判别式.利用根的判别式证明即可.
【详解】证明:,
,
,
无论取任何实数,此方程总有实数根.
19.(1)见解析
(2)
【分析】本题考查一元二次方程根的判别式与方程的根之间的关系,熟练掌握相关知识点是解题关键.
(1)证出根的判别式即可完成;
(2)将k视为数,求出方程的两个根,即可求出k的取值范围.
【详解】(1)证明:,
,
∴方程总有两个实数根;
(2)解:∵,
∴
∴,
∵方程有一个不小于 3的根,
∴,
解得:.
20.(1);
(2)元.
【分析】()设二、三这两个月销售量的月平均增长率为,根据题意列出方程即可求解;
()设商品降价元时,商场获利元,根据题意列出方程即可求解;
本题考查了一元二次方程的应用,根据题意正确列出方程是解题的关键.
【详解】(1)解:设二、三这两个月销售量的月平均增长率为,
由题意得,,
解得,(不合题意,舍去),
答:二、三这两个月销售量的月平均增长率为;
(2)解:设商品降价元时,商场获利元,
由题意得,,
解得,(不合题意,舍去),
答:当商品降价元时,商场获利元.
21.(1)小明的计算结果不对.理由见解析
(2)
(3)方案及作图见解析
【分析】本题考查一元二次方程的解法的运用,矩形的面积公式的运用,扇形的面积公式的运用,
(1)根据条件路的宽度小于,故得出小强的结果不对,应该是;
(2)根据四个扇形的面积=矩形的面积的一半建立方程求出的值即可;
(3)利用同底等高的三角形的面积等于矩形的面积的一半,可得另一方案;
解题的关键是抓住等量关系:花园的面积等于荒地面积的一半.
【详解】(1)解:小明的计算结果不对.理由如下:
设小路宽,
依题意,得:,
解得: ,,
∵荒地的宽为,
∴当时,不符合题意,舍去,
∴,
∴小路的宽为;
(2)依题意得:,
∴,
解得:或(负值不符合题意,舍去),.
∴;
(3)答案不唯一.
如图,取上边长的中点作为三角形的顶点,下边的长的两个端点为三角形的另外两个顶点,则三角形的面积为:,矩形面积为:.
∴此时三角形的面积等于矩形面积的一半.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.下列方程是一元二次方程的是( )
A. B. C. D.
2.方程的根是( )
A. B. C. D.或
3.方程二次项系数,一次项系数和常数项分别是( )
A.1,,1 B.,,1 C.1,3, D.1,3,1
4.如果是方程的一个根,则的值为( )
A.3 B.2 C. D.
5.已知实数a,b满足,则的值为( )
A.3 B.5 C.或5 D.3或
6.在平面直角坐标系中,若直线不经过第四象限,则关于x的方程的实数根的情况为( )
A.无解 B.两个不相等的实数根
C.两个相等的实数根 D.无法确定
7.如图是由一些等边三角形“△”堆成的“金字塔”图形,它的下一排依次比上一排多一个“△”;若第个图形的“△”的个数为45个,则的值为( )
A.7 B.8 C.9 D.10
8.某校截止到2022年底,校园绿化面积为1000平方米.为美化环境,该校计划2024年底绿化面积达到1440平方米.利用方程想想,设这两年绿化面积的年平均增长率为,则依题意列方程为( )
A. B.
C. D.
二、填空题
9.已知,,,求 .
10.小华在解一元二次方程时,只得出一个根是,则被他漏掉的一个根是 .
11.若a为方程的解,则的值为 .
12.美术兴趣小组在中秋节这一天人人相互送一个月饼,共送出56个月饼,美术兴趣小组人数是 .
13.若实数p、q,满足,,且,则的值为 .
14.已知,是方程的两个根,则代数式的值为 .
15.某产品原来成本是25元,按照固定的百分率降低成本,连续两次降低后比一次降低后所剩的成本少4元,设这个百分率为x,可得方程 .
16.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留宽的门.已知计划中的材料可建墙体(不包括门)总长为,则当建成的饲养室总占地面积为时,垂直于墙的一边长为 .
三、解答题
17.解方程∶
(1)
(2)
18.已知关于的一元二次方程.求证:无论取任何实数,此方程总有实数根.
19.已知关于x的方程.
(1)求证:方程总有两个实数根;
(2)若方程有一个不小于 3的根,求实数k的取值范围.
20.物美商场于今年年初以每件元的进价购进一批商品.当商品售价为元时,一月份销售件.二、三月该商品十分畅销.销售量持续走高.在售价不变的基础上,三月底的销售量达到件.设二、三这两个月销售量的月平均增长率不变.
(1)求二、三这两个月销售量的月平均增长率.
(2)从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每降价元,销售量增加件,当商品降价多少元时,商场获利元?
21.在一块长,宽的矩形荒地上建一个花园,要求花园所占面积为荒地面积的一半.图①是小明的设计方案,花园四周小路的宽度相等,通过解方程,小明得到小路的宽为或.图②是小丽的设计方案,其中花园四个角上的扇形都相同.
(1)你认为小明的计算结果对吗? 请说明理由.
(2)请你帮小丽求出图中的(精确到).
(3)你还有其他的设计方案吗? 请在图③中画出你设计的草图,并简要说明.
中小学教育资源及组卷应用平台
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8
答案 A D A C B B C B
1.A
【分析】本题考查了一元二次方程的概念,根据一元二次方程的定义,必须满足四个条件:①未知数的最高次数是2;②二次项系数不为0;③是整式方程;④含有一个未知数.由这四个条件对四个选项进行验证,满足这四个条件者为正确答案.
【详解】解:.是一元二次方程,该选项正确,符合题意;
. 是二元二次方程,该选项错误,不符合题意;
. 不是一元二次方程,该选项错误,不符合题意;
. 不是一元二次方程,该选项错误,不符合题意;
故选:A.
2.D
【分析】本题考查了解一元二次方程,掌握因式分解是解题的关键,根据题意,移项,再提取公因式即可求解.
【详解】解:
移项得,
提取公因式得,,整理得,,
解得,,,
故选:D .
3.A
【分析】本题主要考查了一元二次方程的一般式,对于一元二次方程,其中a、b、c是常数且,a叫做二次项系数,b叫做一次项系数,c叫做常数项,据此可得答案.
【详解】解:把原方程化为一般式为,
∴原方程的二次项系数为1,一次项系数为,常数项为1,
故选:A.
4.C
【分析】本题主要考查了一元二次方程的解,将代入方程,求解即可.
【详解】解:根据题意得:,
,
故选:C.
5.B
【分析】本题主要考查了换元法解一元二次方程,设,则原方程变为,解这个方程即可求得的值.
【详解】解:设,
原方程变为:,
,
解得:,
因为平方和是非负数,
所以的值为5;
故选:B.
6.B
【分析】本题考查了一次函数的性质,根的判别式:一元二次方程的根与有如下关系:当时,方程有两个不相等的实数根;当时,方程有两个相等的实数根;当时,方程无实数根.由直线解析式求得,然后确定的符号即可.
【详解】解:直线不经过第四象限,
,
关于的方程,
,
关于的方程有两个不相等的实数根.
故选:B.
7.C
【分析】此题考查了图形变化类规律问题的解决能力,解一元二次方程,关键是能根据观察图形变化,能够猜想、验证、归纳出此题规律,并能运用此规律解决相关问题.找出规律,第个图形有个“△”,再解一元二次方程即可.
【详解】解:第1个图形有1个,
第2个图形有个,
第3个图形有个,
第4个图形有个,
,
则第个图形有个,
∴,
解得:或(舍),
故选:C.
8.B
【分析】本题考查了一元二次方程的应用,设这两年绿化面积的年平均增长率为,根据“某校截止到2022年底,校园绿化面积为1000平方米.为美化环境,该校计划2024年底绿化面积达到1440平方米”列出方程即可,理解题意,找准等量关系,正确列出方程是解此题的关键.
【详解】解:设这两年绿化面积的年平均增长率为,则依题意列方程为,
故选:B.
9.2
【分析】本题主要考查一元二次方程根与系数的关系,a,b可以看作是一元二次方程的两根,根据根与系数的关系求解即可.
【详解】解:∵,,
∴a,b可以看作是一元二次方程的两根,
∴
故答案为:2.
10.
【分析】本题考查的是一元二次方程的解法,直接利用因式分解的方法解方程即可得到答案.
【详解】解:∵,
∴,
∴或,
解得:,,
∴被他漏掉的一个根是;
故答案为:
11.7
【分析】本题考查了一元二次方程的解,代数式求值,熟练掌握一元二次方程的解与一元二次方程的关系是解题的关键.
由题意得,将其变形与进行关联,即可求解.
【详解】解:∵a为方程的解,
∴,
∴,
∴.
故答案为:7.
12.8
【分析】本题主要考查一元二次方程的应用,找准等量关系列出方程是解题的关键.
根据题意找到“小组的人数(小组人数)”,然后列式计算即可.
【详解】解:设美术兴趣小组有x人,
,
解得:,(负值舍去),
∴美术兴趣小组有8人.
故答案为:8.
13.
【分析】本题考查一元二次方程根的定义,根与系数的关系,完全平方公式及其变式,由已知和是一元二次方程的两根,再根据一元二次方程根与系数的关系求出和的值,再利用完全平方公式的变式即可解决问题,灵活运用一元二次方程根的定义和根的判别式是解题的关键.
【详解】解:∵若实数p、q,满足,,
∴和是一元二次方程,即的两根,
∴,即,
∴,
∵,
∴,
∴,
故答案为:.
14.
【分析】本题考查了根与系数的关系,整式的混合运算,解题的关键是牢记两根之和等于、两根之积等于.
根据先将整式化简,,是方程的两个根,求得,,代入即可求解;
【详解】解: ,是方程的两个根,
,,
将,代入
可得:
故答案为:
15.
【分析】本题主要考查了一元二次方程的应用,解题的关键是设降低的百分率为x,再表示出连续两次降低后的成本,一次降低后的成本,根据连续两次降低后比一次降低后所剩的成本少4元,列出方程即可.
【详解】解:设降低的百分率为x,根据题意得:
.
故答案为:.
16.5
【分析】本题主要考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
设垂直于墙的材料长为米,则平行于墙的材料长为,表示出总面积:,由此列出方程并求得的值即可.
【详解】解:设垂直于墙的材料长为,则平行于墙的材料长为,
根据题意,得.
解得:,
故答案为:5.
17.(1)
(2)
【分析】本题主要考查了解一元二次方程:
(1)利用配方法解方程即可;
(2)先移项,然后利用因式分解法解方程即可.
【详解】(1)解:∵,
∴,
∴,
∴,
解得;
(2)解:∵,
∴,
∴,
∴或,
解得.
18.见解析
【分析】本题考查一元二次方程根的判别式,解题的关键是掌握根的判别式.利用根的判别式证明即可.
【详解】证明:,
,
,
无论取任何实数,此方程总有实数根.
19.(1)见解析
(2)
【分析】本题考查一元二次方程根的判别式与方程的根之间的关系,熟练掌握相关知识点是解题关键.
(1)证出根的判别式即可完成;
(2)将k视为数,求出方程的两个根,即可求出k的取值范围.
【详解】(1)证明:,
,
∴方程总有两个实数根;
(2)解:∵,
∴
∴,
∵方程有一个不小于 3的根,
∴,
解得:.
20.(1);
(2)元.
【分析】()设二、三这两个月销售量的月平均增长率为,根据题意列出方程即可求解;
()设商品降价元时,商场获利元,根据题意列出方程即可求解;
本题考查了一元二次方程的应用,根据题意正确列出方程是解题的关键.
【详解】(1)解:设二、三这两个月销售量的月平均增长率为,
由题意得,,
解得,(不合题意,舍去),
答:二、三这两个月销售量的月平均增长率为;
(2)解:设商品降价元时,商场获利元,
由题意得,,
解得,(不合题意,舍去),
答:当商品降价元时,商场获利元.
21.(1)小明的计算结果不对.理由见解析
(2)
(3)方案及作图见解析
【分析】本题考查一元二次方程的解法的运用,矩形的面积公式的运用,扇形的面积公式的运用,
(1)根据条件路的宽度小于,故得出小强的结果不对,应该是;
(2)根据四个扇形的面积=矩形的面积的一半建立方程求出的值即可;
(3)利用同底等高的三角形的面积等于矩形的面积的一半,可得另一方案;
解题的关键是抓住等量关系:花园的面积等于荒地面积的一半.
【详解】(1)解:小明的计算结果不对.理由如下:
设小路宽,
依题意,得:,
解得: ,,
∵荒地的宽为,
∴当时,不符合题意,舍去,
∴,
∴小路的宽为;
(2)依题意得:,
∴,
解得:或(负值不符合题意,舍去),.
∴;
(3)答案不唯一.
如图,取上边长的中点作为三角形的顶点,下边的长的两个端点为三角形的另外两个顶点,则三角形的面积为:,矩形面积为:.
∴此时三角形的面积等于矩形面积的一半.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
