高中(人教A版数学必修一册)精品同步讲义第2章第05讲第二章一元二次函数、方程和不等式章末题型大总结(12类热点题型讲练)(学生版+解析)
文档属性
| 名称 | 高中(人教A版数学必修一册)精品同步讲义第2章第05讲第二章一元二次函数、方程和不等式章末题型大总结(12类热点题型讲练)(学生版+解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-08 09:05:36 | ||
图片预览





文档简介
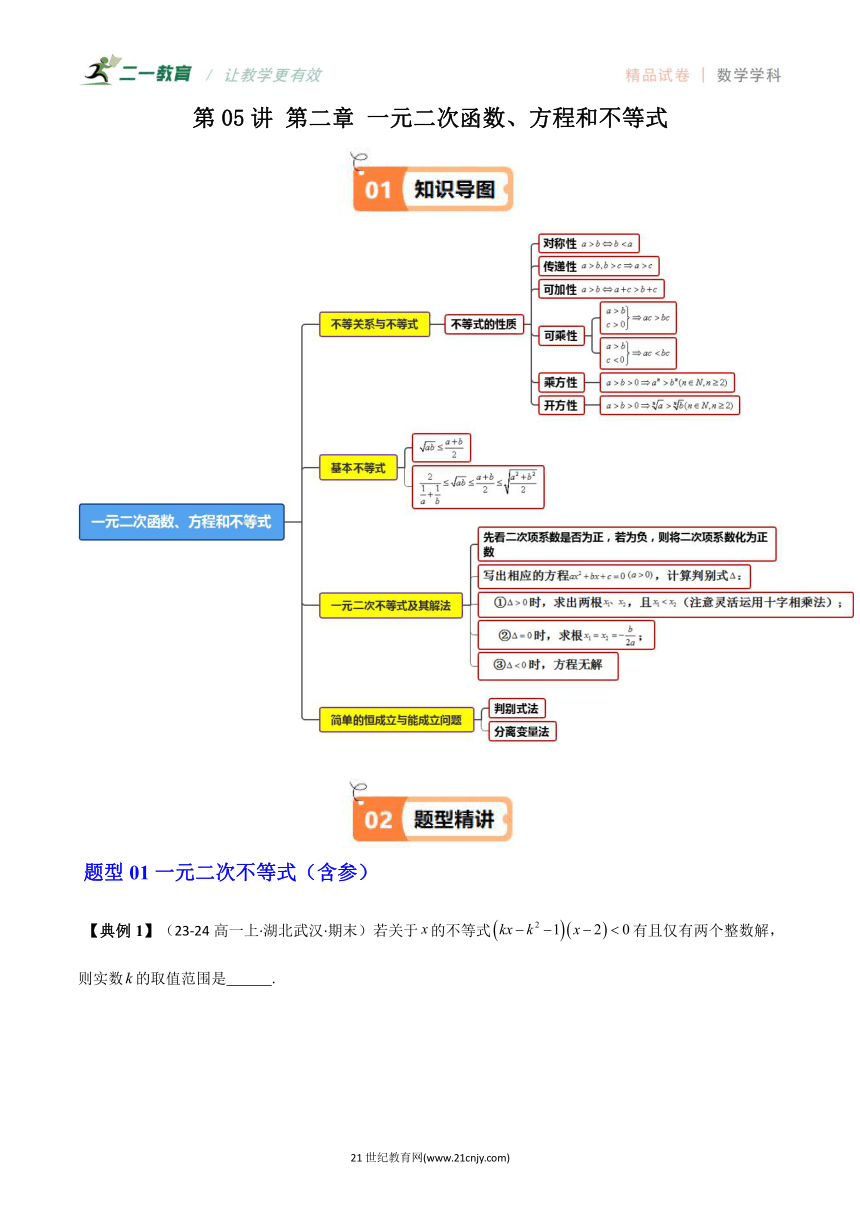
第05讲 第二章 一元二次函数、方程和不等式
题型01一元二次不等式(含参)
【典例1】(23-24高一上·湖北武汉·期末)若关于的不等式有且仅有两个整数解,则实数的取值范围是 .
【典例2】(23-24高一上·云南德宏·期末)已知.
(1)若恒成立,求实数的取值范围;
(2)求不等式的解集.
【变式1】(23-24高一上·北京密云·期末)已知函数.
(1)若不等式的解集为,求的值;
(2)若不等式对任意的恒成立,求实数的取值范围;
(3)解关于的不等式.
【变式2】(23-24高一上·重庆·期末)已知关于的不等式.
(1)若该不等式的解集为,求和的值;
(2)若,求该不等式的解集.
题型02由一元二次不等式的解确定参数
【典例1】(23-24高一下·广东湛江·开学考试)关于的不等式的解集为,则的值为( )
A. B. C. D.
【典例2】(23-24高一下·江西上饶·开学考试)已知不等式.
(1)若不等式的解集是或,求的值;
(2)若不等式的解集是,求的取值范围.
【变式1】(23-24高一上·云南昭通·期末)不等式的解集是,则的值是( )
A. B. C. D.
【变式2】(多选)(23-24高一下·云南·阶段练习)若关于的不等式的解集为,则下列说法正确的是( )
A.
B.
C.的解集为
D.的最小值为
【变式3】(23-24高二上·甘肃白银·期末)已知一元二次不等式的解集为,求的值.
题型03一元二次方程根的分布问题
【典例1】(23-24高一上·辽宁大连·期中)关于x的方程至少有一个负根的充要条件是( )
A. B. C. D.
【典例2】(23-24高一上·山东·期中)已知函数.
(1)若关于的不等式的解集为,求的值;
(2)当时,方程有一个根大于1,一个根小于1,求实数的取值范围.
【变式2】(2024高二下·浙江·学业考试)已知正实数,满足,则的最小值为 .
【变式3】(2024·陕西西安·三模)已知,,则的最小值为 .
题型08与基本不等式有关的恒成立问题
【典例1】(23-24高一上·浙江杭州·期末)若正实数、满足,且恒成立,则实数的取值范围是( )
A. B.
C. D.
【典例2】(23-24高一上·重庆·期末)当,且满足时,有恒成立,则的取值范围为( )
A. B. C. D.
【变式1】(23-24高一上·山东滨州·期末)已知,,且,若恒成立,则实数的取值范围为( )
A. B.
C. D.
【变式2】(2024·江西·一模)已知正数x,y满足,若不等式恒成立,则实数a的取值范围是 .
【变式3】(23-24高一下·江苏镇江·开学考试)设,若恒成立,则的取值范围为 .
题型09不等式与实际问题的关联
【典例1】(23-24高三下·山东济宁·开学考试)一家商店使用一架两臂不等长的天平称黄金.一位顾客到店里购买黄金,售货员现将的砝码放在天平的左盘中,取出黄金放在天平右盘中使天平平衡;将天平左右盘清空后,再将的砝码放在天平右盘中,再取出黄金放在天平的左盘中,使天平平衡;最后将两次称得的黄金交给顾客.则( )
A. B.
C. D.以上都有可能
题型10函数与方程的思想
【典例1】(23-24高一上·江苏宿迁·期中)已知关于的一元二次不等式的解集为,且实数,满足,则实数的取值范围是( )
A. B. C.或 D.或
【典例2】(23-24高一上·浙江杭州·期中)不等式的解集是,则不等式的解集是(用集合表示) .
【变式1】(多选)(23-24高一上·湖南娄底·期末)已知关于x的不等式(,)的解集为,则下列结论正确的是( )
A. B.的最大值为
C.的最小值为4 D.的最小值为
题型11分类讨论思想
【典例1】(23-24高一上·江西抚州·期末)已知函数
(1)是否存在实数使得关于的不等式的解集为,若存在.求实数的值或取值范围,若不存在,请说明理由;
(2)若关于的不等式的解集是,集合,若,求实数的取值范围.
【典例2】(23-24高二上·陕西咸阳·阶段练习)已知命题:“”是真命题
(1)求实数m的取值集合B;
(2)设关于x的不等式的解集为A,若“”是“”的充分不必要条件,求实数a的取值范围.
题型12化归与转化的思想
【典例1】(多选)(23-24高二上·云南大理·期末)已知且,若恒成立,则实数可取( )
A.0 B.1 C.2 D.3
【典例2】(23-24高一上·山西运城·期末)已知正实数a,b满足,且不等式恒成立,则实数m的取值范围是 .
【变式1】(多选)(23-24高一上·福建泉州·期中)已知,且不等式恒成立,则的值可以是( )
A.2 B.3 C.4 D.521世纪教育网(www.21cnjy.com)
第05讲 第二章 一元二次函数、方程和不等式
题型01一元二次不等式(含参)
【典例1】(23-24高一上·湖北武汉·期末)若关于的不等式有且仅有两个整数解,则实数的取值范围是 .
【答案】或,
【分析】分、、三种情况讨论,当时得到,即可求出的取值范围.
【详解】①当时,解得,不符合题意;
故,关于的不等式,即,
②当时,不等式即,解得或,
即它的解集为或,,不满足题意;
③当时,不等式即,
由于,当且仅当时取等号,故它的解集为,,
由题意,即,解得或,
则实数的取值范围为或,.
故答案为:或,
【典例2】(23-24高一上·云南德宏·期末)已知.
(1)若恒成立,求实数的取值范围;
(2)求不等式的解集.
【答案】(1)
(2)答案见解析
【分析】(1)由恒成立,即恒成立,即得,从而可求解.
(2)由即,然后对分情况讨论,从而可求解.
【详解】(1)∵ 恒成立,
∴ 对恒成立,
故,化简得,解得,
故实数的取值范围.
(2),即;
当时,不等式的解为或,
当时,不等式的解为或,
当时,不等式的解为.
【变式1】(23-24高一上·北京密云·期末)已知函数.
(1)若不等式的解集为,求的值;
(2)若不等式对任意的恒成立,求实数的取值范围;
(3)解关于的不等式.
【答案】(1)
(2)
(3)解集见解析
【分析】(1)根据一元二次不等式解集与一元二次方程根的关系解出即可;
(2)根据一元二次不等式恒成立,即可由判别式求解;
(3)分解因式,结合分类讨论,即可由一元二次不等式解的特征求解.
【详解】(1)因为不等式的解集为,
所以方程的两根分别为,
根据韦达定理可知,,解得;
(2)不等式对任意的恒成立,
即对任意的恒成立,所以,
即,解得,所以实数a的取值范围为;
(3)即,
当时,不等式的解为或,
当时,不等式的解为或,
当时,不等式的解为,
综上所述,当时,不等式的解集为,
当时,不等式的解集为.
【变式2】(23-24高一上·重庆·期末)已知关于的不等式.
(1)若该不等式的解集为,求和的值;
(2)若,求该不等式的解集.
【答案】(1)
(2)答案见解析
【分析】(1)由二次不等式的解得二次方程的根,利用韦达定理建立方程求解即可;
(2)分类讨论解一元二次不等式即可.
【详解】(1)因为不等式的解集为,
所以二次方程的根为,
由韦达定理可得,解得;
(2)若,则不等式为,即,
令,得,当,即时,;
当,即时,无解;当,即时,.
综上:时,解集为;时,解集为;时,解集为.
题型02由一元二次不等式的解确定参数
【典例1】(23-24高一下·广东湛江·开学考试)关于的不等式的解集为,则的值为( )
A. B. C. D.
【答案】C
【分析】将问题转化为是方程的两个实根,再直接代入方程得到关于的方程组,解之即可得解.
【详解】因为不等式的解集为,
所以是方程的两个实根,
所以,解得,
所以.
故选:C.
【典例2】(23-24高一下·江西上饶·开学考试)已知不等式.
(1)若不等式的解集是或,求的值;
(2)若不等式的解集是,求的取值范围.
【答案】(1)
(2)
【分析】(1)由一元二次不等式的性质可知方程的两根为,再由韦达定理可解.
(2)由二次函数的性质可得关于的不等式组,解出即可.
【详解】(1)由题意可知方程的两个根分别为,
由韦达定理可知,解得,经检验满足题设.
(2)若不等式的解集是,即恒成立,则满足,解得.
【变式1】(23-24高一上·云南昭通·期末)不等式的解集是,则的值是( )
A. B. C. D.
【答案】D
【分析】由题意得,,和是方程的根,然后结合方程的根与系数关系即可求解.
【详解】因为不等式的解集是,
所以,和是方程的根,
所以,即,,则.
故选:D.
【变式2】(多选)(23-24高一下·云南·阶段练习)若关于的不等式的解集为,则下列说法正确的是( )
A.
B.
C.的解集为
D.的最小值为
【答案】BC
【分析】题意说明的两根为,代入法1得的值,从而可逐项判断.
【详解】根据题意,关于的不等式的解集为,
所以的两根为,
则,解得,
所以,即A错误,B正确;
且为,解得或,
所以的解集为,C正确;
,
所以的最大值为,D错误.
故选:BC
【变式3】(23-24高二上·甘肃白银·期末)已知一元二次不等式的解集为,求的值.
【答案】
【分析】依题意关于的一元二次方程的两根为、且,利用韦达定理得到方程组,解得即可.
【详解】因为一元二次不等式的解集为,
所以关于的一元二次方程的两根为、且,
所以,解得,所以.
题型03一元二次方程根的分布问题
【典例1】(23-24高一上·辽宁大连·期中)关于x的方程至少有一个负根的充要条件是( )
A. B. C. D.
【答案】D
【分析】根据实数是不是为零进行分类讨论,结合根的判别式及韦达定理即可得解.
【详解】当时,方程为,此时方程的根为负根,
当时,方程,
当方程有二个负根时,则有,
当方程有一个负根一个正根时,则有,
综上所述:当关于x的方程至少有一个负根时,有,
即关于x的方程至少有一个负根的充要条件是.
故选:D.
【典例2】(23-24高一上·山东·期中)已知函数.
(1)若关于的不等式的解集为,求的值;
(2)当时,方程有一个根大于1,一个根小于1,求实数的取值范围.
【答案】(1)
(2)
【分析】(1)由题意可知,和1是方程的两个实数根,结合韦达定理可求a,b的值;
(2)由于二次函数的图象开口向上,所以可将“一根大于1,一根小于1”转化为,即a的范围可求.
【详解】(1)由题意可知,和1是方程的两个实数根,
所以,
解得.
(2)当时,,因为函数的图象开口向上,且的根一根大于1,一根小于1,
所以,即,解得或,
所以实数的取值范围是.
【变式1】(23-24高一上·北京·期中)如果关于的一元二次方程有两个不同的正数实数根,那么的取值范围为( )
A. B. C. D.
【答案】A
【分析】根据方程有两个不同的正实根,则两根之和大于零,两根之积大于零及,列出不等式组,解出即可.
【详解】因为关于的一元二次方程有两个不同的正数实数根,
则有,
故选:A
【变式2】(23-24高一上·浙江金华·阶段练习)已知关于的方程 ,当方程的根满足下列条件时,求的取值范围.
(1)有两个实数根,且一个比2大,一个比2小;
(2)至少有一个正根.
【答案】(1)
(2)
【分析】(1)设,则由题意可得,求解即可得答案;
(2)采用正难则反的原则再进行分类讨论即可.
【详解】(1)设,
则由题意可得,解得.
(2)关于x的方程无实数根时,,
解得,
关于x的方程有两个负实数根时,
,解得,
所以关于x的方程无实数根时或有两个负实数根时,
可得关于x的方程至少有一个正实数根,则.
题型04一元二次不等式的恒成立(有解)问题
【典例1】(23-24高一上·河北·阶段练习)若命题“”为假命题,则的最大值为( )
A. B. C. D.
【答案】A
【分析】由题意可得命题“”是真命题,则在上恒成立,结合二次函数的性质即可求解.
【详解】由题意知命题“”是真命题.
因为,所以.
当时,函数的最大值为6,
则的最小值为,所以,即的最大值为.
故选:A.
【典例2】(23-24高一上·江苏盐城·期中)设函数.
(1)若对于恒成立,求的取值范围;
(2)若对于恒成立,求的取值范围.
【答案】(1)
(2)
【分析】(1)先转化为对于恒成立,再求的最小值,即得m的取值范围.
(2)题设条件可以转化为对于恒成立,将分别代入不等式,即可求出的范围.
【详解】(1)由题意得,在恒成立,
即在恒成立,
∵对一切实数恒成立,
∴在恒成立,
∵函数在上单调递减,在上单调递增,
∴,∴在上的最小值为,∴.
故的取值范围为.
(2)对于恒成立,
对于恒成立,
,
解得,
故的取值范围为.
【变式1】(23-24高一上·安徽合肥·期中)命题“,”是假命题,则实数的取值范围是( )
A. B. C. D.
【答案】D
【分析】原命题的否定为真命题,由二次不等式恒成立的条件,求实数的取值范围.
【详解】由题意,原命题的否定“,”为真命题,
令,则当时,,
故,解得.
所以实数的取值范围是.
故选:D
【变式2】(23-24高一下·上海·开学考试)若对于任意,恒成立,则实数的取值范围是 .
【答案】
【分析】分和两种情况讨论即可得解.
【详解】①当时,不等式恒成立,所以符合要求;
②当时,题意等价于,即,解得,
综上可知.
故答案为:.
【变式3】(23-24高一上·江苏盐城·期末)关于的不等式在上有解,则实数的取值范围是 .
【答案】
【分析】
根据题意将不等式转化为在能成立即可,再由二次函数性质求出即可得的取值范围是.
【详解】由不等式以及可得,
依题意可知即可,
令,
又,由可得,
利用二次函数性质可知,即可得;
即实数的取值范围是.
故答案为:
【变式4】(23-24高一上·江苏镇江·期中)若关于的不等式在区间内有解,则实数的取值范围 .
【答案】
【分析】
根据二次函数的性质,结合配方法进行求解即可.
【详解】,
设,
,该二次函数的对称轴为,开口向下,
当时,,
要想关于的不等式在区间内有解,
只需,
所以实数的取值范围为,
故答案为:
题型05“1”的代换转化为基本不等式求最值
【典例1】(23-24高一下·广西南宁·开学考试)已知,且,则的最小值为( )
A. B.1 C. D.2
【答案】C
【分析】依题意可得,再利用乘“1”法及基本不等式计算可得.
【详解】因为,且,所以,
所以
,
当且仅当,即时取等号,
所以的最小值为.
故选:C.
【典例2】(23-24高一上·安徽蚌埠·期末)已知正数满足,若恒成立,则实数的取值范围为 .
【答案】
【分析】
根据基本不等式求得不等式左边的最小值,建立不等式,解出即可.
【详解】因为且,所以
,当且仅当时取等号.
因为不等式恒成立,
所以,解得.
故答案为:.
【变式1】(23-24高一下·黑龙江大庆·开学考试)若正数满足,则的最小值为
【答案】6
【分析】先把已知变形为,再利用“1”的妙用,结合基本不等式求最值.
【详解】由得,
所以,
当且仅当,即时,等号成立.
故答案为:6.
【变式2】(23-24高一上·山东菏泽·阶段练习)若两个正实数满足,且不等式恒成立,则实数的取值范围为 .
【答案】
【分析】
根据等式变形,利用常值代换法凑项,运用基本不等式求得即得.
【详解】
因为两个正实数 满足,则,
故
,当且仅当时取等号,
因不等式恒成立,则,故.
故答案为:.
【变式3】(2024·四川成都·模拟预测)已知实数,若,则的最小值为 .
【答案】/
【分析】由乘“1”的方法,利用基本不等式求最值.
【详解】由,
,
当且仅当,即时,等号成立,
所以的最小值为为.
故答案为:.
题型06基本不等式(条件最值问题)
【典例1】(2024·山西·三模)已知正实数x,y满足,则的最小值为( )
A. B. C. D.
【答案】A
【分析】根据题意分析可知,利用基本不等式运算求解.
【详解】因为正实数x,y满足,则,
则,
当且仅当,即时,等号成立,
所以的最小值为.
故选:A.
【典例2】(多选)(23-24高三下·重庆大足·阶段练习)设正实数,,且满足,则( )
A. B.
C. D.
【答案】AD
【分析】对于A项,通过题设求出,代入所求式消元,凑项运用基本不等式即得;对于B项,直接运用基本不等式将其转化成关于的不等式求解即得;对于C项,运用完全平方式将其转化成关于的二次函数,通过其图象单调性即得;对于D项,通分后将其化成关于的分式函数,求其值域即得.
【详解】对于A项,由可得:,
因,故,将其代入可得:
当且仅当时等号成立,故A项正确;
对于B项,由可得,
因,故得:,则,
当且仅当时等号成立,故B项错误;
对于C项,由,
设,由上分析知,,
则在上单调递增,故,即C项错误;
对于D项,由,
由上分析知,则,
故,即,故D项正确.
故选:AD.
【变式1】(多选)(23-24高三上·云南昆明·阶段练习)已知正数满足,则( )
A.的最小值为3 B.的最小值为6
C.的最小值为 D.的最小值为
【答案】BCD
【分析】根据题意,结合基本不等式,逐项判定,即可求解.
【详解】因为,
令,则,解得,即,
则,其中所有不等式等号成立均当且,所以A错误,B正确;
对两边同除以可得,由,可得,
所以,当且仅当时,等号成立,所以C正确;
由可得,
则,
当且仅当即时,等号成立,故D正确.
故选:BCD.
【变式2】(2024高二下·浙江·学业考试)已知正实数,满足,则的最小值为 .
【答案】/
【分析】依题意可得,令,,即可得到且,,目标式子,利用基本不等式计算可得.
【详解】因为正实数,满足,
即,令,,则且,,
所以,
当且仅当,即,时取等号.
故答案为:
【变式3】(2024·陕西西安·三模)已知,,则的最小值为 .
【答案】/
【分析】依题意可得,再由基本不等式计算可得.
【详解】因为,且,
所以,
所以,
当且仅当,即,时,等号成立,
故的最小值为.
故答案为:.
题型08与基本不等式有关的恒成立问题
【典例1】(23-24高一上·浙江杭州·期末)若正实数、满足,且恒成立,则实数的取值范围是( )
A. B.
C. D.
【答案】B
【分析】依题意可得,利用乘“1”法及基本不等式求出的最小值,即可得到,解得即可.
【详解】因为正实数、满足,
即,所以,
所以,
当且仅当,即,时取等号,
因为正实数、满足,且恒成立,
所以,解得,即实数的取值范围是.
故选:B.
【典例2】(23-24高一上·重庆·期末)当,且满足时,有恒成立,则的取值范围为( )
A. B. C. D.
【答案】A
【分析】把恒成立问题转化成求最值问题,利用基本不等式求出的最小值,然后解二次不等式即可.
【详解】因为即且,
所以,
当且仅当,即时等号成立,
因为不等式恒成立,所以,
即,解得,故的取值范围为.
故选:A
【变式1】(23-24高一上·山东滨州·期末)已知,,且,若恒成立,则实数的取值范围为( )
A. B.
C. D.
【答案】B
【分析】将问题转化为,利用“1”的代换以及基本不等式求解,从而得到,求解不等式,即可得到答案.
【详解】因为不等式恒成立,
则,
因为,,由可得,
所以,
当且仅当,即,时取等号,
故,
所以,即,解得,
则实数的取值范围是.
故选:B.
【变式2】(2024·江西·一模)已知正数x,y满足,若不等式恒成立,则实数a的取值范围是 .
【答案】
【分析】
将变形为,利用均值不等式求的最小值即可求解.
【详解】因为,
所以
,
所以
,等号成立当且仅当,
所以,,
故实数a的取值范围是.
故答案为:
【点睛】关键点点睛:解题关键是先得到,再进一步结合乘“1”法即可顺利得解.
【变式3】(23-24高一下·江苏镇江·开学考试)设,若恒成立,则的取值范围为 .
【答案】
【分析】因为,所以将转化为然后与相乘然后运用基本不等式求解.
【详解】因为,所以
.
当且仅当时,即时等号成立,
所以.
故答案为:.
题型09不等式与实际问题的关联
【典例1】(23-24高三下·山东济宁·开学考试)一家商店使用一架两臂不等长的天平称黄金.一位顾客到店里购买黄金,售货员现将的砝码放在天平的左盘中,取出黄金放在天平右盘中使天平平衡;将天平左右盘清空后,再将的砝码放在天平右盘中,再取出黄金放在天平的左盘中,使天平平衡;最后将两次称得的黄金交给顾客.则( )
A. B.
C. D.以上都有可能
【答案】A
【分析】根据杠杆原理可得,,进而可根据基本不等式求解.
【详解】设天平左臂长为,右臂长为,且,则有,,即 ,,
所以,,
又因为,所以.
故选:A
【典例2】(23-24高一上·甘肃临夏·期末)某单位建造一间地面面积为12平方米的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过5米,房屋正面的造价为400元/平方米,房屋侧面的造价为150元/平方米,屋顶和地面的造价费用合计为5800元,如果墙高为3米,且不计房屋背面的费用,当侧面的长度为多少时,总造价最低?最低总造价是多少元?
【答案】当侧面的长度为4米时,总造价最低.最低总造价是13000元
【分析】根据题意得到函数表达式,利用基本不等式求出最小值即可.
【详解】由题可知
因为,当且仅当,即时取等号,
所以在时取最小值,
于是当侧面的长度为米时,总造价最低.最低总造价是元.
【变式1】(23-24高三上·山西吕梁·阶段练习)第19届亚运会于2023年9月23日至10月8日在中国杭州举行,参赛的各国运动员在比赛、训练之余,都爱逛逛杭州亚运会特许商品零售店,开启“买买买”模式.某商店售卖的一种亚运会纪念章,每枚的最低售价为15元,若每枚按最低售价销售,每天能卖出45枚,每枚售价每提高1元,日销售量将减少3枚,为了使这批纪念章每天获得600元以上的销售收入,则这批纪念章的销售单价x(单位:元)的取值范围是( )
A. B. C. D.
【答案】B
【分析】根据题中条件列出不等式,解出即可.
【详解】由题意,得,
即,∴,
解得.又每枚的最低售价为15元,∴.
故选:B.
【变式2】(23-24高一上·浙江湖州·阶段练习)若不计空气阻力,竖直上抛的物体距离抛出点的高度与时间满足关系式:,其中取.已知一名同学以初速度竖直上抛一排球,排球能够在抛出点以上的位置停留 秒时间.
【答案】
【分析】根据题意求得关系式,令,得到,即可求解.
【详解】由题意,竖直上抛的物体距离抛出点的高度与时间满足关系式,
因为,所以,
令,得,即,解得,,
所以停留的时间为.
故答案为:.
【变式3】(23-24高一上·贵州贵阳·阶段练习)一家车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量(单位:辆)与创造的价值(单位:元)之间有如下的关系:.若这家工厂希望在一个星期内利用这条流水线创收6000元以上,则在一个星期内大约应该生产 (填写区间范围)辆摩托车?
【答案】51~59
【分析】依据题意列出不等关系,解不等式再根据实际意义即可求出需生产51~59辆摩托车.
【详解】根据题意可知,
转化为不等式,即可得,
解得;
所以应该生产51~59辆摩托车.
故答案为:51~59
【变式4】(23-24高一上·四川成都·期中)石室中学“跳蚤市场”活动即将开启,学生们在该活动中的商品所卖款项将用来支持慈善事业.为了在这次活动中最大限度地筹集资金,某班进行了前期调查.若商品进货
因为,,所以,可得,
当且仅当时取等号,所以的最大值为,所以B正确;
由,
当且仅当时,即时取等号,所以的最小值为,所以C错误;
由,
当且仅当时,即时,等号成立,
所以的最小值为,所以D正确.
故选:ABD
题型11分类讨论思想
【典例1】(23-24高一上·江西抚州·期末)已知函数
(1)是否存在实数使得关于的不等式的解集为,若存在.求实数的值或取值范围,若不存在,请说明理由;
(2)若关于的不等式的解集是,集合,若,求实数的取值范围.
【答案】(1)存在
(2)
【分析】(1)设在恒成立,可得时不满足,当时,结合二次函数的开口方向、判别式可得答案;
(2)由题意可设在上恒成立,分、、讨论,结合一元二次不等式恒成立可得答案.
【详解】(1)设在恒成立,
显然当,即时不满足在上恒成立;
当时,
,
综上,存在使得的解集为;
(2)由题意可设在上恒成立,
②当,即时,,符合题意;
③当,即时,,
又“”是“”的充分不必要条件,
∴是的真子集,即包含于,
∴,∴;
综上,实数a的取值范围为.
题型12化归与转化的思想
【典例1】(多选)(23-24高二上·云南大理·期末)已知且,若恒成立,则实数可取( )
A.0 B.1 C.2 D.3
【答案】AB
【分析】利用基本不等式单位“1”的应用,求出的最小值,从而可求解.
【详解】由题意知,,
所以,
当且仅当时取等号,所以,解得,所以A、B正确.
故选:AB.
【典例2】(23-24高一上·山西运城·期末)已知正实数a,b满足,且不等式恒成立,则实数m的取值范围是 .
【答案】
【分析】分离参数得恒成立,即,然后结合基本不等式求解即可.
【详解】因为正实数a,b满足,,
所以,
因为,
当且仅当,即时取等号,
所以,
所以不等式恒成立,只需即可.
故答案为:
【变式1】(多选)(23-24高一上·福建泉州·期中)已知,且不等式恒成立,则的值可以是( )
A.2 B.3 C.4 D.5
【答案】AB
【分析】令,,(当且仅当时取等号),(当且仅当时取等号),所以,再利用基本不等式计算出的最小值,即可求出的取值范围,即可得解.
【详解】令,,因为,,所以,,
则(当且仅当时取等号),(当且仅当时取等号),
则,
当且仅当时取等号,即时取等号,
因为不等式恒成立,
所以,则.
故选:AB
21世纪教育网(www.21cnjy.com)
题型01一元二次不等式(含参)
【典例1】(23-24高一上·湖北武汉·期末)若关于的不等式有且仅有两个整数解,则实数的取值范围是 .
【典例2】(23-24高一上·云南德宏·期末)已知.
(1)若恒成立,求实数的取值范围;
(2)求不等式的解集.
【变式1】(23-24高一上·北京密云·期末)已知函数.
(1)若不等式的解集为,求的值;
(2)若不等式对任意的恒成立,求实数的取值范围;
(3)解关于的不等式.
【变式2】(23-24高一上·重庆·期末)已知关于的不等式.
(1)若该不等式的解集为,求和的值;
(2)若,求该不等式的解集.
题型02由一元二次不等式的解确定参数
【典例1】(23-24高一下·广东湛江·开学考试)关于的不等式的解集为,则的值为( )
A. B. C. D.
【典例2】(23-24高一下·江西上饶·开学考试)已知不等式.
(1)若不等式的解集是或,求的值;
(2)若不等式的解集是,求的取值范围.
【变式1】(23-24高一上·云南昭通·期末)不等式的解集是,则的值是( )
A. B. C. D.
【变式2】(多选)(23-24高一下·云南·阶段练习)若关于的不等式的解集为,则下列说法正确的是( )
A.
B.
C.的解集为
D.的最小值为
【变式3】(23-24高二上·甘肃白银·期末)已知一元二次不等式的解集为,求的值.
题型03一元二次方程根的分布问题
【典例1】(23-24高一上·辽宁大连·期中)关于x的方程至少有一个负根的充要条件是( )
A. B. C. D.
【典例2】(23-24高一上·山东·期中)已知函数.
(1)若关于的不等式的解集为,求的值;
(2)当时,方程有一个根大于1,一个根小于1,求实数的取值范围.
【变式2】(2024高二下·浙江·学业考试)已知正实数,满足,则的最小值为 .
【变式3】(2024·陕西西安·三模)已知,,则的最小值为 .
题型08与基本不等式有关的恒成立问题
【典例1】(23-24高一上·浙江杭州·期末)若正实数、满足,且恒成立,则实数的取值范围是( )
A. B.
C. D.
【典例2】(23-24高一上·重庆·期末)当,且满足时,有恒成立,则的取值范围为( )
A. B. C. D.
【变式1】(23-24高一上·山东滨州·期末)已知,,且,若恒成立,则实数的取值范围为( )
A. B.
C. D.
【变式2】(2024·江西·一模)已知正数x,y满足,若不等式恒成立,则实数a的取值范围是 .
【变式3】(23-24高一下·江苏镇江·开学考试)设,若恒成立,则的取值范围为 .
题型09不等式与实际问题的关联
【典例1】(23-24高三下·山东济宁·开学考试)一家商店使用一架两臂不等长的天平称黄金.一位顾客到店里购买黄金,售货员现将的砝码放在天平的左盘中,取出黄金放在天平右盘中使天平平衡;将天平左右盘清空后,再将的砝码放在天平右盘中,再取出黄金放在天平的左盘中,使天平平衡;最后将两次称得的黄金交给顾客.则( )
A. B.
C. D.以上都有可能
题型10函数与方程的思想
【典例1】(23-24高一上·江苏宿迁·期中)已知关于的一元二次不等式的解集为,且实数,满足,则实数的取值范围是( )
A. B. C.或 D.或
【典例2】(23-24高一上·浙江杭州·期中)不等式的解集是,则不等式的解集是(用集合表示) .
【变式1】(多选)(23-24高一上·湖南娄底·期末)已知关于x的不等式(,)的解集为,则下列结论正确的是( )
A. B.的最大值为
C.的最小值为4 D.的最小值为
题型11分类讨论思想
【典例1】(23-24高一上·江西抚州·期末)已知函数
(1)是否存在实数使得关于的不等式的解集为,若存在.求实数的值或取值范围,若不存在,请说明理由;
(2)若关于的不等式的解集是,集合,若,求实数的取值范围.
【典例2】(23-24高二上·陕西咸阳·阶段练习)已知命题:“”是真命题
(1)求实数m的取值集合B;
(2)设关于x的不等式的解集为A,若“”是“”的充分不必要条件,求实数a的取值范围.
题型12化归与转化的思想
【典例1】(多选)(23-24高二上·云南大理·期末)已知且,若恒成立,则实数可取( )
A.0 B.1 C.2 D.3
【典例2】(23-24高一上·山西运城·期末)已知正实数a,b满足,且不等式恒成立,则实数m的取值范围是 .
【变式1】(多选)(23-24高一上·福建泉州·期中)已知,且不等式恒成立,则的值可以是( )
A.2 B.3 C.4 D.521世纪教育网(www.21cnjy.com)
第05讲 第二章 一元二次函数、方程和不等式
题型01一元二次不等式(含参)
【典例1】(23-24高一上·湖北武汉·期末)若关于的不等式有且仅有两个整数解,则实数的取值范围是 .
【答案】或,
【分析】分、、三种情况讨论,当时得到,即可求出的取值范围.
【详解】①当时,解得,不符合题意;
故,关于的不等式,即,
②当时,不等式即,解得或,
即它的解集为或,,不满足题意;
③当时,不等式即,
由于,当且仅当时取等号,故它的解集为,,
由题意,即,解得或,
则实数的取值范围为或,.
故答案为:或,
【典例2】(23-24高一上·云南德宏·期末)已知.
(1)若恒成立,求实数的取值范围;
(2)求不等式的解集.
【答案】(1)
(2)答案见解析
【分析】(1)由恒成立,即恒成立,即得,从而可求解.
(2)由即,然后对分情况讨论,从而可求解.
【详解】(1)∵ 恒成立,
∴ 对恒成立,
故,化简得,解得,
故实数的取值范围.
(2),即;
当时,不等式的解为或,
当时,不等式的解为或,
当时,不等式的解为.
【变式1】(23-24高一上·北京密云·期末)已知函数.
(1)若不等式的解集为,求的值;
(2)若不等式对任意的恒成立,求实数的取值范围;
(3)解关于的不等式.
【答案】(1)
(2)
(3)解集见解析
【分析】(1)根据一元二次不等式解集与一元二次方程根的关系解出即可;
(2)根据一元二次不等式恒成立,即可由判别式求解;
(3)分解因式,结合分类讨论,即可由一元二次不等式解的特征求解.
【详解】(1)因为不等式的解集为,
所以方程的两根分别为,
根据韦达定理可知,,解得;
(2)不等式对任意的恒成立,
即对任意的恒成立,所以,
即,解得,所以实数a的取值范围为;
(3)即,
当时,不等式的解为或,
当时,不等式的解为或,
当时,不等式的解为,
综上所述,当时,不等式的解集为,
当时,不等式的解集为.
【变式2】(23-24高一上·重庆·期末)已知关于的不等式.
(1)若该不等式的解集为,求和的值;
(2)若,求该不等式的解集.
【答案】(1)
(2)答案见解析
【分析】(1)由二次不等式的解得二次方程的根,利用韦达定理建立方程求解即可;
(2)分类讨论解一元二次不等式即可.
【详解】(1)因为不等式的解集为,
所以二次方程的根为,
由韦达定理可得,解得;
(2)若,则不等式为,即,
令,得,当,即时,;
当,即时,无解;当,即时,.
综上:时,解集为;时,解集为;时,解集为.
题型02由一元二次不等式的解确定参数
【典例1】(23-24高一下·广东湛江·开学考试)关于的不等式的解集为,则的值为( )
A. B. C. D.
【答案】C
【分析】将问题转化为是方程的两个实根,再直接代入方程得到关于的方程组,解之即可得解.
【详解】因为不等式的解集为,
所以是方程的两个实根,
所以,解得,
所以.
故选:C.
【典例2】(23-24高一下·江西上饶·开学考试)已知不等式.
(1)若不等式的解集是或,求的值;
(2)若不等式的解集是,求的取值范围.
【答案】(1)
(2)
【分析】(1)由一元二次不等式的性质可知方程的两根为,再由韦达定理可解.
(2)由二次函数的性质可得关于的不等式组,解出即可.
【详解】(1)由题意可知方程的两个根分别为,
由韦达定理可知,解得,经检验满足题设.
(2)若不等式的解集是,即恒成立,则满足,解得.
【变式1】(23-24高一上·云南昭通·期末)不等式的解集是,则的值是( )
A. B. C. D.
【答案】D
【分析】由题意得,,和是方程的根,然后结合方程的根与系数关系即可求解.
【详解】因为不等式的解集是,
所以,和是方程的根,
所以,即,,则.
故选:D.
【变式2】(多选)(23-24高一下·云南·阶段练习)若关于的不等式的解集为,则下列说法正确的是( )
A.
B.
C.的解集为
D.的最小值为
【答案】BC
【分析】题意说明的两根为,代入法1得的值,从而可逐项判断.
【详解】根据题意,关于的不等式的解集为,
所以的两根为,
则,解得,
所以,即A错误,B正确;
且为,解得或,
所以的解集为,C正确;
,
所以的最大值为,D错误.
故选:BC
【变式3】(23-24高二上·甘肃白银·期末)已知一元二次不等式的解集为,求的值.
【答案】
【分析】依题意关于的一元二次方程的两根为、且,利用韦达定理得到方程组,解得即可.
【详解】因为一元二次不等式的解集为,
所以关于的一元二次方程的两根为、且,
所以,解得,所以.
题型03一元二次方程根的分布问题
【典例1】(23-24高一上·辽宁大连·期中)关于x的方程至少有一个负根的充要条件是( )
A. B. C. D.
【答案】D
【分析】根据实数是不是为零进行分类讨论,结合根的判别式及韦达定理即可得解.
【详解】当时,方程为,此时方程的根为负根,
当时,方程,
当方程有二个负根时,则有,
当方程有一个负根一个正根时,则有,
综上所述:当关于x的方程至少有一个负根时,有,
即关于x的方程至少有一个负根的充要条件是.
故选:D.
【典例2】(23-24高一上·山东·期中)已知函数.
(1)若关于的不等式的解集为,求的值;
(2)当时,方程有一个根大于1,一个根小于1,求实数的取值范围.
【答案】(1)
(2)
【分析】(1)由题意可知,和1是方程的两个实数根,结合韦达定理可求a,b的值;
(2)由于二次函数的图象开口向上,所以可将“一根大于1,一根小于1”转化为,即a的范围可求.
【详解】(1)由题意可知,和1是方程的两个实数根,
所以,
解得.
(2)当时,,因为函数的图象开口向上,且的根一根大于1,一根小于1,
所以,即,解得或,
所以实数的取值范围是.
【变式1】(23-24高一上·北京·期中)如果关于的一元二次方程有两个不同的正数实数根,那么的取值范围为( )
A. B. C. D.
【答案】A
【分析】根据方程有两个不同的正实根,则两根之和大于零,两根之积大于零及,列出不等式组,解出即可.
【详解】因为关于的一元二次方程有两个不同的正数实数根,
则有,
故选:A
【变式2】(23-24高一上·浙江金华·阶段练习)已知关于的方程 ,当方程的根满足下列条件时,求的取值范围.
(1)有两个实数根,且一个比2大,一个比2小;
(2)至少有一个正根.
【答案】(1)
(2)
【分析】(1)设,则由题意可得,求解即可得答案;
(2)采用正难则反的原则再进行分类讨论即可.
【详解】(1)设,
则由题意可得,解得.
(2)关于x的方程无实数根时,,
解得,
关于x的方程有两个负实数根时,
,解得,
所以关于x的方程无实数根时或有两个负实数根时,
可得关于x的方程至少有一个正实数根,则.
题型04一元二次不等式的恒成立(有解)问题
【典例1】(23-24高一上·河北·阶段练习)若命题“”为假命题,则的最大值为( )
A. B. C. D.
【答案】A
【分析】由题意可得命题“”是真命题,则在上恒成立,结合二次函数的性质即可求解.
【详解】由题意知命题“”是真命题.
因为,所以.
当时,函数的最大值为6,
则的最小值为,所以,即的最大值为.
故选:A.
【典例2】(23-24高一上·江苏盐城·期中)设函数.
(1)若对于恒成立,求的取值范围;
(2)若对于恒成立,求的取值范围.
【答案】(1)
(2)
【分析】(1)先转化为对于恒成立,再求的最小值,即得m的取值范围.
(2)题设条件可以转化为对于恒成立,将分别代入不等式,即可求出的范围.
【详解】(1)由题意得,在恒成立,
即在恒成立,
∵对一切实数恒成立,
∴在恒成立,
∵函数在上单调递减,在上单调递增,
∴,∴在上的最小值为,∴.
故的取值范围为.
(2)对于恒成立,
对于恒成立,
,
解得,
故的取值范围为.
【变式1】(23-24高一上·安徽合肥·期中)命题“,”是假命题,则实数的取值范围是( )
A. B. C. D.
【答案】D
【分析】原命题的否定为真命题,由二次不等式恒成立的条件,求实数的取值范围.
【详解】由题意,原命题的否定“,”为真命题,
令,则当时,,
故,解得.
所以实数的取值范围是.
故选:D
【变式2】(23-24高一下·上海·开学考试)若对于任意,恒成立,则实数的取值范围是 .
【答案】
【分析】分和两种情况讨论即可得解.
【详解】①当时,不等式恒成立,所以符合要求;
②当时,题意等价于,即,解得,
综上可知.
故答案为:.
【变式3】(23-24高一上·江苏盐城·期末)关于的不等式在上有解,则实数的取值范围是 .
【答案】
【分析】
根据题意将不等式转化为在能成立即可,再由二次函数性质求出即可得的取值范围是.
【详解】由不等式以及可得,
依题意可知即可,
令,
又,由可得,
利用二次函数性质可知,即可得;
即实数的取值范围是.
故答案为:
【变式4】(23-24高一上·江苏镇江·期中)若关于的不等式在区间内有解,则实数的取值范围 .
【答案】
【分析】
根据二次函数的性质,结合配方法进行求解即可.
【详解】,
设,
,该二次函数的对称轴为,开口向下,
当时,,
要想关于的不等式在区间内有解,
只需,
所以实数的取值范围为,
故答案为:
题型05“1”的代换转化为基本不等式求最值
【典例1】(23-24高一下·广西南宁·开学考试)已知,且,则的最小值为( )
A. B.1 C. D.2
【答案】C
【分析】依题意可得,再利用乘“1”法及基本不等式计算可得.
【详解】因为,且,所以,
所以
,
当且仅当,即时取等号,
所以的最小值为.
故选:C.
【典例2】(23-24高一上·安徽蚌埠·期末)已知正数满足,若恒成立,则实数的取值范围为 .
【答案】
【分析】
根据基本不等式求得不等式左边的最小值,建立不等式,解出即可.
【详解】因为且,所以
,当且仅当时取等号.
因为不等式恒成立,
所以,解得.
故答案为:.
【变式1】(23-24高一下·黑龙江大庆·开学考试)若正数满足,则的最小值为
【答案】6
【分析】先把已知变形为,再利用“1”的妙用,结合基本不等式求最值.
【详解】由得,
所以,
当且仅当,即时,等号成立.
故答案为:6.
【变式2】(23-24高一上·山东菏泽·阶段练习)若两个正实数满足,且不等式恒成立,则实数的取值范围为 .
【答案】
【分析】
根据等式变形,利用常值代换法凑项,运用基本不等式求得即得.
【详解】
因为两个正实数 满足,则,
故
,当且仅当时取等号,
因不等式恒成立,则,故.
故答案为:.
【变式3】(2024·四川成都·模拟预测)已知实数,若,则的最小值为 .
【答案】/
【分析】由乘“1”的方法,利用基本不等式求最值.
【详解】由,
,
当且仅当,即时,等号成立,
所以的最小值为为.
故答案为:.
题型06基本不等式(条件最值问题)
【典例1】(2024·山西·三模)已知正实数x,y满足,则的最小值为( )
A. B. C. D.
【答案】A
【分析】根据题意分析可知,利用基本不等式运算求解.
【详解】因为正实数x,y满足,则,
则,
当且仅当,即时,等号成立,
所以的最小值为.
故选:A.
【典例2】(多选)(23-24高三下·重庆大足·阶段练习)设正实数,,且满足,则( )
A. B.
C. D.
【答案】AD
【分析】对于A项,通过题设求出,代入所求式消元,凑项运用基本不等式即得;对于B项,直接运用基本不等式将其转化成关于的不等式求解即得;对于C项,运用完全平方式将其转化成关于的二次函数,通过其图象单调性即得;对于D项,通分后将其化成关于的分式函数,求其值域即得.
【详解】对于A项,由可得:,
因,故,将其代入可得:
当且仅当时等号成立,故A项正确;
对于B项,由可得,
因,故得:,则,
当且仅当时等号成立,故B项错误;
对于C项,由,
设,由上分析知,,
则在上单调递增,故,即C项错误;
对于D项,由,
由上分析知,则,
故,即,故D项正确.
故选:AD.
【变式1】(多选)(23-24高三上·云南昆明·阶段练习)已知正数满足,则( )
A.的最小值为3 B.的最小值为6
C.的最小值为 D.的最小值为
【答案】BCD
【分析】根据题意,结合基本不等式,逐项判定,即可求解.
【详解】因为,
令,则,解得,即,
则,其中所有不等式等号成立均当且,所以A错误,B正确;
对两边同除以可得,由,可得,
所以,当且仅当时,等号成立,所以C正确;
由可得,
则,
当且仅当即时,等号成立,故D正确.
故选:BCD.
【变式2】(2024高二下·浙江·学业考试)已知正实数,满足,则的最小值为 .
【答案】/
【分析】依题意可得,令,,即可得到且,,目标式子,利用基本不等式计算可得.
【详解】因为正实数,满足,
即,令,,则且,,
所以,
当且仅当,即,时取等号.
故答案为:
【变式3】(2024·陕西西安·三模)已知,,则的最小值为 .
【答案】/
【分析】依题意可得,再由基本不等式计算可得.
【详解】因为,且,
所以,
所以,
当且仅当,即,时,等号成立,
故的最小值为.
故答案为:.
题型08与基本不等式有关的恒成立问题
【典例1】(23-24高一上·浙江杭州·期末)若正实数、满足,且恒成立,则实数的取值范围是( )
A. B.
C. D.
【答案】B
【分析】依题意可得,利用乘“1”法及基本不等式求出的最小值,即可得到,解得即可.
【详解】因为正实数、满足,
即,所以,
所以,
当且仅当,即,时取等号,
因为正实数、满足,且恒成立,
所以,解得,即实数的取值范围是.
故选:B.
【典例2】(23-24高一上·重庆·期末)当,且满足时,有恒成立,则的取值范围为( )
A. B. C. D.
【答案】A
【分析】把恒成立问题转化成求最值问题,利用基本不等式求出的最小值,然后解二次不等式即可.
【详解】因为即且,
所以,
当且仅当,即时等号成立,
因为不等式恒成立,所以,
即,解得,故的取值范围为.
故选:A
【变式1】(23-24高一上·山东滨州·期末)已知,,且,若恒成立,则实数的取值范围为( )
A. B.
C. D.
【答案】B
【分析】将问题转化为,利用“1”的代换以及基本不等式求解,从而得到,求解不等式,即可得到答案.
【详解】因为不等式恒成立,
则,
因为,,由可得,
所以,
当且仅当,即,时取等号,
故,
所以,即,解得,
则实数的取值范围是.
故选:B.
【变式2】(2024·江西·一模)已知正数x,y满足,若不等式恒成立,则实数a的取值范围是 .
【答案】
【分析】
将变形为,利用均值不等式求的最小值即可求解.
【详解】因为,
所以
,
所以
,等号成立当且仅当,
所以,,
故实数a的取值范围是.
故答案为:
【点睛】关键点点睛:解题关键是先得到,再进一步结合乘“1”法即可顺利得解.
【变式3】(23-24高一下·江苏镇江·开学考试)设,若恒成立,则的取值范围为 .
【答案】
【分析】因为,所以将转化为然后与相乘然后运用基本不等式求解.
【详解】因为,所以
.
当且仅当时,即时等号成立,
所以.
故答案为:.
题型09不等式与实际问题的关联
【典例1】(23-24高三下·山东济宁·开学考试)一家商店使用一架两臂不等长的天平称黄金.一位顾客到店里购买黄金,售货员现将的砝码放在天平的左盘中,取出黄金放在天平右盘中使天平平衡;将天平左右盘清空后,再将的砝码放在天平右盘中,再取出黄金放在天平的左盘中,使天平平衡;最后将两次称得的黄金交给顾客.则( )
A. B.
C. D.以上都有可能
【答案】A
【分析】根据杠杆原理可得,,进而可根据基本不等式求解.
【详解】设天平左臂长为,右臂长为,且,则有,,即 ,,
所以,,
又因为,所以.
故选:A
【典例2】(23-24高一上·甘肃临夏·期末)某单位建造一间地面面积为12平方米的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过5米,房屋正面的造价为400元/平方米,房屋侧面的造价为150元/平方米,屋顶和地面的造价费用合计为5800元,如果墙高为3米,且不计房屋背面的费用,当侧面的长度为多少时,总造价最低?最低总造价是多少元?
【答案】当侧面的长度为4米时,总造价最低.最低总造价是13000元
【分析】根据题意得到函数表达式,利用基本不等式求出最小值即可.
【详解】由题可知
因为,当且仅当,即时取等号,
所以在时取最小值,
于是当侧面的长度为米时,总造价最低.最低总造价是元.
【变式1】(23-24高三上·山西吕梁·阶段练习)第19届亚运会于2023年9月23日至10月8日在中国杭州举行,参赛的各国运动员在比赛、训练之余,都爱逛逛杭州亚运会特许商品零售店,开启“买买买”模式.某商店售卖的一种亚运会纪念章,每枚的最低售价为15元,若每枚按最低售价销售,每天能卖出45枚,每枚售价每提高1元,日销售量将减少3枚,为了使这批纪念章每天获得600元以上的销售收入,则这批纪念章的销售单价x(单位:元)的取值范围是( )
A. B. C. D.
【答案】B
【分析】根据题中条件列出不等式,解出即可.
【详解】由题意,得,
即,∴,
解得.又每枚的最低售价为15元,∴.
故选:B.
【变式2】(23-24高一上·浙江湖州·阶段练习)若不计空气阻力,竖直上抛的物体距离抛出点的高度与时间满足关系式:,其中取.已知一名同学以初速度竖直上抛一排球,排球能够在抛出点以上的位置停留 秒时间.
【答案】
【分析】根据题意求得关系式,令,得到,即可求解.
【详解】由题意,竖直上抛的物体距离抛出点的高度与时间满足关系式,
因为,所以,
令,得,即,解得,,
所以停留的时间为.
故答案为:.
【变式3】(23-24高一上·贵州贵阳·阶段练习)一家车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量(单位:辆)与创造的价值(单位:元)之间有如下的关系:.若这家工厂希望在一个星期内利用这条流水线创收6000元以上,则在一个星期内大约应该生产 (填写区间范围)辆摩托车?
【答案】51~59
【分析】依据题意列出不等关系,解不等式再根据实际意义即可求出需生产51~59辆摩托车.
【详解】根据题意可知,
转化为不等式,即可得,
解得;
所以应该生产51~59辆摩托车.
故答案为:51~59
【变式4】(23-24高一上·四川成都·期中)石室中学“跳蚤市场”活动即将开启,学生们在该活动中的商品所卖款项将用来支持慈善事业.为了在这次活动中最大限度地筹集资金,某班进行了前期调查.若商品进货
因为,,所以,可得,
当且仅当时取等号,所以的最大值为,所以B正确;
由,
当且仅当时,即时取等号,所以的最小值为,所以C错误;
由,
当且仅当时,即时,等号成立,
所以的最小值为,所以D正确.
故选:ABD
题型11分类讨论思想
【典例1】(23-24高一上·江西抚州·期末)已知函数
(1)是否存在实数使得关于的不等式的解集为,若存在.求实数的值或取值范围,若不存在,请说明理由;
(2)若关于的不等式的解集是,集合,若,求实数的取值范围.
【答案】(1)存在
(2)
【分析】(1)设在恒成立,可得时不满足,当时,结合二次函数的开口方向、判别式可得答案;
(2)由题意可设在上恒成立,分、、讨论,结合一元二次不等式恒成立可得答案.
【详解】(1)设在恒成立,
显然当,即时不满足在上恒成立;
当时,
,
综上,存在使得的解集为;
(2)由题意可设在上恒成立,
②当,即时,,符合题意;
③当,即时,,
又“”是“”的充分不必要条件,
∴是的真子集,即包含于,
∴,∴;
综上,实数a的取值范围为.
题型12化归与转化的思想
【典例1】(多选)(23-24高二上·云南大理·期末)已知且,若恒成立,则实数可取( )
A.0 B.1 C.2 D.3
【答案】AB
【分析】利用基本不等式单位“1”的应用,求出的最小值,从而可求解.
【详解】由题意知,,
所以,
当且仅当时取等号,所以,解得,所以A、B正确.
故选:AB.
【典例2】(23-24高一上·山西运城·期末)已知正实数a,b满足,且不等式恒成立,则实数m的取值范围是 .
【答案】
【分析】分离参数得恒成立,即,然后结合基本不等式求解即可.
【详解】因为正实数a,b满足,,
所以,
因为,
当且仅当,即时取等号,
所以,
所以不等式恒成立,只需即可.
故答案为:
【变式1】(多选)(23-24高一上·福建泉州·期中)已知,且不等式恒成立,则的值可以是( )
A.2 B.3 C.4 D.5
【答案】AB
【分析】令,,(当且仅当时取等号),(当且仅当时取等号),所以,再利用基本不等式计算出的最小值,即可求出的取值范围,即可得解.
【详解】令,,因为,,所以,,
则(当且仅当时取等号),(当且仅当时取等号),
则,
当且仅当时取等号,即时取等号,
因为不等式恒成立,
所以,则.
故选:AB
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
