(人教A版选择性必修一册)高中数学精品讲义第1章第07讲拓展一:异面直线所成角(传统法与向量法)(学生版+解析)
文档属性
| 名称 | (人教A版选择性必修一册)高中数学精品讲义第1章第07讲拓展一:异面直线所成角(传统法与向量法)(学生版+解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-08 00:00:00 | ||
图片预览




文档简介
第07讲 拓展一:异面直线所成角(传统法与向量法)
1、(传统法)核心技巧:平移使相交
具体操作,通过平移一条(或2条),使异面直线转化为相交直线,然后在三角形中利用余弦定理求角
2、(向量法)用向量运算求两条直线所成角
已知,为两异面直线,,与,分别是,上的任意两点,,所成的角为,则
①
②.
题型01求异面直线所成角(定值)(传统法)
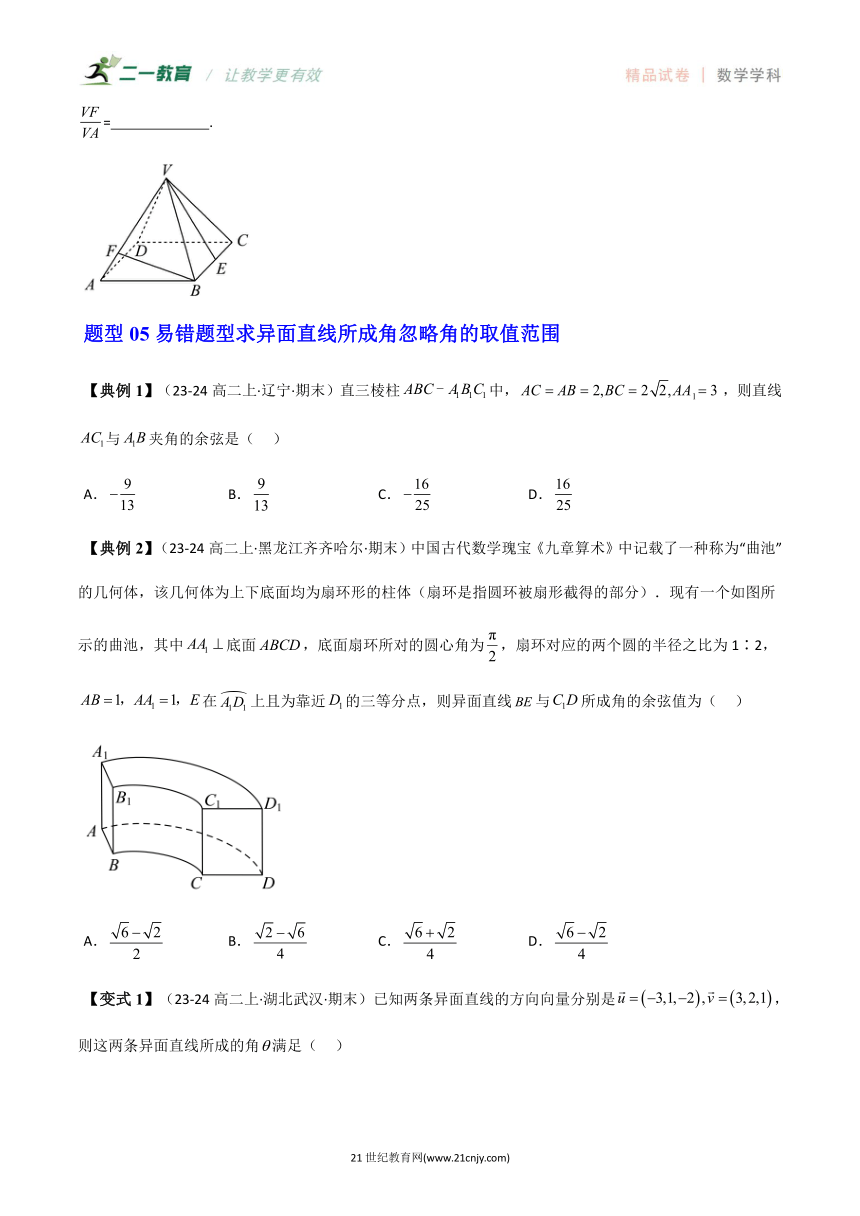
【典例1】(23-24高一下·山东烟台·阶段练习)已知在长方体中,,直线与平面所成角的正弦值为为线段的中点,则直线与直线所成角的余弦值为( )
A. B. C. D.
【典例2】(23-24高一下·浙江·阶段练习)在正三棱柱中,面ABC,,则异面直线与所成角的余弦值为( )
A. B. C. D.
【变式1】(2024·重庆·模拟预测)如图,已知四边形是平行四边形,分别是的中点,点P在平面内的射影为与平面所成角的正切值为2,则直线与所成角的余弦值为( )
题型02求异面直线所成角(定值)(向量法)
【典例1】(2024·辽宁沈阳·模拟预测)已知直三棱柱中,,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
【典例2】(23-24高三上·广西·开学考试)正多面体被古希腊圣哲认为是构成宇宙的基本元素,加上它们的多种变体,一直是科学、艺术、哲学灵感的源泉之一.如图,该几何体是一个高为4的正八面体,G为的中点,则异面直线与所成角的正弦值为 .
【典例3】(2024高一下·全国·专题练习)如图,已知是圆柱下底面圆的圆心,为圆柱的一条母线,为圆柱下底面圆周上一点,,,为等腰直角三角形,则异面直线与所成角的余弦值为 .
【变式1】(2024·湖北武汉·模拟预测)已知菱形,,将沿对角线折起,使以四点为顶点的三棱锥体积最大,则异面直线与所成角的余弦值为( )
A. B. C. D.
【变式2】(23-24高三下·四川德阳·期末)正四面体中,、分别是和的中点,则和所成角的大小是 .
【变式3】(23-24高二上·广东茂名·期末)长方体中,,,点F是底面的中心,则直线与直线所成角的余弦值为 .
题型03求异面直线所成角(最值或范围)
【典例1】(23-24高二下·山东烟台·阶段练习)如图,在边长为1的正方体中,点在上,点在平面内,设直线与直线所成角为.若直线到平面的距离为,则的最小值为 .
【典例2】(23-24高二上·浙江金华·阶段练习)如图,在多面体中,平面,平面平面,是边长为的等边三角形,,.
(1)求点B到平面的距离;
(2)若M为的中点,N为线段上的动点,设异面直线与所成角为,求的最大值及此时的值
【变式3】(23-24高二上·吉林通化·期末)如图,在正四棱锥中,二面角为60°,E为的中点.已知F为直线上一点,且F与A不重合,若异面直线与所成角为60°,则= .
题型05易错题型求异面直线所成角忽略角的取值范围
【典例1】(23-24高二上·辽宁·期末)直三棱柱中,,则直线与夹角的余弦是( )
A. B. C. D.
【典例2】(23-24高二上·黑龙江齐齐哈尔·期末)中国古代数学瑰宝《九章算术》中记载了一种称为“曲池”的几何体,该几何体为上下底面均为扇环形的柱体(扇环是指圆环被扇形截得的部分).现有一个如图所示的曲池,其中底面,底面扇环所对的圆心角为,扇环对应的两个圆的半径之比为1∶2,在上且为靠近的三等分点,则异面直线与所成角的余弦值为( )
A. B. C. D.
【变式1】(23-24高二上·湖北武汉·期末)已知两条异面直线的方向向量分别是,则这两条异面直线所成的角满足( )
A. B.
C. D.
【变式2】(23-24高二上·山东枣庄·阶段练习)如图,在四棱锥中,底面为正方形,底面,,E为上一点,且,则异面直线与所成角的余弦值为( )
A. B. C. D.
21世纪教育网(www.21cnjy.com)
第07讲 拓展一:异面直线所成角(传统法与向量法)
1、(传统法)核心技巧:平移使相交
具体操作,通过平移一条(或2条),使异面直线转化为相交直线,然后在三角形中利用余弦定理求角
2、(向量法)用向量运算求两条直线所成角
已知,为两异面直线,,与,分别是,上的任意两点,,所成的角为,则
①
②.
题型01求异面直线所成角(定值)(传统法)
【典例1】(23-24高一下·山东烟台·阶段练习)已知在长方体中,,直线与平面所成角的正弦值为为线段的中点,则直线与直线所成角的余弦值为( )
A. B. C. D.
【答案】A
【分析】结合条件根据线面角的定义求得,连接,根据异面直线夹角的定义,利用余弦定理求解即可.
【详解】连接,因为平面,所以为直线与平面所成角,
设,则,
所以,所以,
连接连接,由长方体的性质知,且,
所以四边形为平行四边形,
所以,则或其补角即为直线与直线所成角,
在中,,
所以由余弦定理得,
即直线与直线所成角的余弦值为.
故选:A
【典例2】(23-24高一下·浙江·阶段练习)在正三棱柱中,面ABC,,则异面直线与所成角的余弦值为( )
A. B. C. D.
【答案】A
【分析】分别取的中点,可得是异面直线与所成角即为与所成角(或其补角),在中,由余弦定理求解即可.
【详解】分别取的中点,
连接,所以,
所以异面直线与所成角即为与所成角(或其补角),
即,设,所以,
,
所以在中,所以,
所以异面直线与所成角的余弦值为.
故选:A.
【变式1】(2024·重庆·模拟预测)如图,已知四边形是平行四边形,分别是的中点,点P在平面内的射影为与平面所成角的正切值为2,则直线与所成角的余弦值为( )
A. B. C. D.
【答案】A
【分析】根据题意,由条件可证,则直线与所成的角为,然后结合条件以及余弦定理代入计算,即可得到结果.
【详解】
如图,取的中点E,连接.因为分别是的中点,
所以.
因为四边形是平行四边形,所以.
因为N为的中点,所以,所以.
故四边形为平行四边形,所以,
所以直线与所成的角为.
连接,因为点P在平面内的射影为N,所以平面,
所以与平面所成的角为,所以.
不妨令,则,所以,
所以,
在中,
由余弦定理得.
故选:A.
【变式2】(23-24高一下·安徽阜阳·期中)如图,在正方体中,M,N分别为C1D1和CC1的中点,则异面直线AM与BN所成角的余弦值为( )
A. B. C. D.
【答案】A
【分析】分别为的中点,或其补角为AM与BN所成的角,设正方体的边长为,余弦定理求解即可.
【详解】取AB的中点,的中点,连接,
又M,N分别为和的中点,正方体中,,,
四边形为平行四边形,有,
同理有,则或其补角为AM与BN所成的角,
连接EF,设正方体的边长为,则,
,,
所以,
即异面直线AM与BN所成角的余弦值为.
故选:A.
【变式3】(23-24高三上·河南鹤壁·期中)如图,在正三棱柱中,,,则直线与直线所成角的正切值为 .
【答案】/
【分析】根据给定条件,作出直线与直线所成的角,再借助余弦定理求出余弦值即可求解.
【详解】在正三棱柱中,连接交于O点,取的中点F,连接OF,
显然是的中点,则,是与所成的角或其补角,
在中,,,,
,,
所以直线与直线所成角的正切值为.
故答案为:
【变式4】(2024·全国·模拟预测)在三棱锥中,,,,为的中点,则异面直线与所成角的余弦值是 .
【答案】
【分析】先根据异面直线所成角的定义确定为异面直线与所成的角或其补角;再根据勾股定理求出,余弦定理求出.,进而得出;最后在中,利用余弦定理即可求出.
【详解】取的中点,连接,如图所示:
因为为的中点,为的中点,
则根据三角形的中位线定理可得,且.
所以为异面直线与所成的角或其补角.
因为在中,,,,
所以,则.
又,所以.
又在中,,,
所以由余弦定理可得:.
又因为在中,,
所以由余弦定理可得:.
则在中,由余弦定理可得,,
所以异面直线与所成角的余弦值为.
故答案为:.
题型02求异面直线所成角(定值)(向量法)
【典例1】(2024·辽宁沈阳·模拟预测)已知直三棱柱中,,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
【答案】C
【分析】根据空间向量法求线线角解决即可.
【详解】以为原点,在平面过作的垂线交于,
以为轴,以为轴,以为轴,建立空间直角坐标系,
因为直三棱柱中,,,,
所以,
所以,
设异面直线与所成角为,
所以.
故选:C.
【典例2】(23-24高三上·广西·开学考试)正多面体被古希腊圣哲认为是构成宇宙的基本元素,加上它们的多种变体,一直是科学、艺术、哲学灵感的源泉之一.如图,该几何体是一个高为4的正八面体,G为的中点,则异面直线与所成角的正弦值为 .
【答案】
【分析】依题意,求出棱长,建立空间直角坐标系,借助向量求出异面直线夹角的余弦值,再转换为正弦值即可.
【详解】
连接交于点,连接,
因为该几何体是一个高为4的正八面体,
所以,,,
设棱长为,则,,
所以在中,,即,解得,
以所在直线为轴,建立如图所示空间直角坐标系,
则,
所以,
设异面直线与夹角为,
则,
因为,
所以异面直线与所成角的正弦值,
故答案为:.
【典例3】(2024高一下·全国·专题练习)如图,已知是圆柱下底面圆的圆心,为圆柱的一条母线,为圆柱下底面圆周上一点,,,为等腰直角三角形,则异面直线与所成角的余弦值为 .
【答案】
【分析】可借助等角定理得到或其补角即异面直线与所成的角,结合余弦定理计算;或借助空间向量的线性运算得到,再利用夹角公式计算.
【详解】方法一 :
如图,过点作交圆柱的上底面于点,连接,,
则由圆柱的性质易证四边形为矩形,所以,
所以或其补角即异面直线与所成的角,
在中,,所以,
因为为等腰直角三角形,且,所以,
所以,又,
所以,
即异面直线与所成角的余弦值为.
方法二 :
在中,,
所以,,
因为为等腰直角三角形,且,所以,
易知,所以,,,
所以,
所以,
则异面直线与所成角的余弦值为.
故答案为:.
【变式1】(2024·湖北武汉·模拟预测)已知菱形,,将沿对角线折起,使以四点为顶点的三棱锥体积最大,则异面直线与所成角的余弦值为( )
A. B. C. D.
【答案】C
【分析】当三棱锥的体积最大时,平面平面,以E为原点,分别为轴的正方向建立空间直角坐标系,求出向量的坐标,根据向量夹角的坐标表示可解.
【详解】记的 中点分别为,因为,所以,
同理,,记,
因为,所以,
所以,,
易知,当平面平面时,三棱锥的体积最大,此时,
以E为原点,分别为轴的正方向建立空间直角坐标系,
则
所以,
所以,
所以异面直线与所成角的余弦值为.
故选:C
【变式2】(23-24高三下·四川德阳·期末)正四面体中,、分别是和的中点,则和所成角的大小是 .
【答案】/
【分析】构造辅助线,利用中位线定理得到是和所成角,然后结合向量数量积的变形即可求解.
【详解】取中点,连接,令棱长为,
因为、分别是和的中点,
所以,,,,
所以是和所成角,
又,
,
,
所以 ,
,,
所以,
所以,即和所成角的大小为.
故答案为:
【变式3】(23-24高二上·广东茂名·期末)长方体中,,,点F是底面的中心,则直线与直线所成角的余弦值为 .
【答案】/
【分析】建立空间直角坐标系,利用坐标进行计算即可.
【详解】如图所示,建立如下空间直角坐标系,
依题可得,,
则,
所以,
故直线与直线所成角的余弦值为,
故答案为:.
题型03求异面直线所成角(最值或范围)
【典例1】(23-24高二下·山东烟台·阶段练习)如图,在边长为1的正方体中,点在上,点在平面内,设直线与直线所成角为.若直线到平面的距离为,则的最小值为 .
【答案】
【分析】建立空间直角坐标系,利用向量法表示出到面的距离,进而求出点坐标,过作平面的平行平面,得到点的轨迹,再利用向量法求线线角,进而求其最值即可.
【详解】因为直线到平面的距离为,
所以必有面,即点到平面的距离为,
如图建立空间直角坐标系,设,又,
则,
设面的法向量为,
则,取得,
则,解得,即,
过作平面的平行平面,与正方体的截面为,
分别为线段和线段的中点,则
所以在直线上,
设,
又,则,
当时,,
当时,,
又,所以,
则的最小值为.
故答案为:
【典例2】(23-24高二上·浙江金华·阶段练习)如图,在多面体中,平面,平面平面,是边长为的等边三角形,,.
(1)求点B到平面的距离;
(2)若M为的中点,N为线段上的动点,设异面直线与所成角为,求的最大值及此时的值
【答案】(1)
(2);
【分析】
(1)说明两两垂直,建立空间直角坐标系,求出相关点的坐标,求出平面的法向量,根据空间距离的向量求法,即可求得答案;
(2)设,表示出N点坐标,即可求得坐标,结合的坐标,根据空间角的向量求法,即可求得的最大值及此时的值.
【详解】(1)设的中点为O,连接,而,则,
是边长为的等边三角形,故,则,
平面平面,平面平面,平面,
故平面,平面,故,
又是边长为的等边三角形,的中点为O,故,
故以所在直线为轴,建立空间直角坐标系,
则,
,
设平面的一个法向量为,则,
令,则,又,
故点B到平面的距离为;
(2)M为的中点,即为O点;
N为线段上的动点,设,
而,即,故点,
故,而,
设异面直线与所成角为,则
,
令,则,
故,
令,则,即为,
当时,取得最小值,
即,即时,取得最大值,
即的最大值为,此时的值为.
【典例3】(23-24高三下·湖南长沙·开学考试)三棱锥中,平面,,.,点是面内的动点(不含边界),,则异面直线与所成角的余弦值的取值范围为( )
A. B. C. D.
【答案】A
【分析】建立空间直角坐标系,由,可得,再利用线线角的向量求法求解即得.
【详解】由平面平面,得,
又平面,则平面,
平面,则,又,平面,
因此平面,而平面,则,
如图,以为坐标原点,的方向为轴正方向建立空间直角坐标系,
则,设,
,由,得,
,设异面直线与所成角为,
则,
令,则,
显然函数在上单调递增,此时,,
所以异面直线与所成角的余弦值的取值范围为.
故选:A
【点睛】思路点睛:求空间角余弦的最值或范围问题,根据给定条件,选定变量,将该角的余弦建立起变量的函数,求出函数最值或范围即可.
【变式1】(23-24高二上·山东潍坊·期末)在直三棱柱中,,,平面经过点A,且直线与平面所成的角为30°,过点作平面的垂线,垂足为H,则点到平面的距离为 ,直线与BH所成角的范围为 .
【答案】 2
【分析】利用,得出在以为直径的球面上,其时可得出到平面的距离,由直线与平面所成的角为30°,得在以为轴,顶角为的圆锥面上,从而得出的轨迹是圆,然后建立如图所示的空间直角坐标系,利用空间向量法求得与所成角的余弦值,角的范围.
【详解】如图,连接,因为,,所以,
所以在以为直径的球面上,又直线与平面所成角为,而即为直线与平面所成的角,因此,因此在以为轴,顶角为的圆锥面上,
过作于点,则,其中的长即为到平面的距离.
所以在圆锥的底面圆上,为圆心,半径为,
以为轴,为轴,过与垂直的直线的为轴建立如图所示的空间直角坐标系,
则,设,
,取的一个方向向量为,
,
又,所以,
所以直线与所成角的范围是,即,
故答案为:;.
【变式2】(23-24高二上·黑龙江哈尔滨·期末)如图,在长方体中,E是的中点,点F是AD上一点,,,,动点P在上底面上,且满足三棱锥的体积等于1,则直线CP与所成角的余弦值的最大值为 .
【答案】/
【分析】建立空间直角坐标系,设,通过向量法算出点P到平面BFE的距离,结合三棱锥的体积等于1可得到,再通过向量法计算直线CP与所成角的余弦值的范围,继而算出答案
【详解】以D为坐标原点,分别以所在直线为x,y,z轴建立空间直角坐标系,
,则,,
,
设平面的法向量为,则,令,得,
而,则点P到平面BFE的距离,
又,
在等腰中,到的高为,则
而,于是,
解得或,由,得,则,
设直线与所成的角为,则,,
,当且仅当时取等号,
所以的最大值为,
故答案为:
【点睛】方法点睛:求点到平面的距离可以利用几何法,作出点到平面的垂线段求解;也可以用向量法,求出平面的法向量,再求出这一点与平面内任意一点确定的向量在法向量的投影即可.
【变式3】(23-24高二上·河南洛阳·期中)如图,四边形和均为正方形,且,平面平面分别为的中点,为线段上的动点,则异面直线与所成角的余弦值最大时, .
【答案】
【分析】根据题意建立空间直角坐标系,求出异面直线与所成角的余弦值最大时点位置,进而求出大小.
【详解】
由题可以为原点,建立空间直角坐标系如图所示:
则,设,
则,
设异面直线与所成角为,
则,
令,
则,
当时,,
当时,,
令,则,
因为,
当时,有最小值,
此时有最大值,
由得,,
则异面直线与所成角的余弦值最大时,
即,,
所以.
故答案为:
题型04已知线线角求参数
【典例1】(23-24高三上·河北唐山·期末)如图,在四棱柱中,底面,且底面为菱形,,,,为的中点,在上,在平面内运动(不与重合),且平面,异面直线与所成角的余弦值为,则的最大值为 .
【答案】/
【分析】连接交于点,推导出平面,然后以点为坐标原点,、、的方向分别为、、轴的正方向建立空间直角坐标系,设,其中,利用空间向量法可求得的值,求出点的坐标为,求出的最小值,即可求得的最大值.
【详解】连接交于点,平面,平面,则,
因为四边形为菱形,则,
,、平面,平面,
以点为坐标原点,、、的方向分别为、、轴的正方向建立如下图所示的空间直角坐标系,
则、、、、、、,
易知平面的一个法向量为,
因为平面,所以,,
设点,其中,则,
由已知可得,
因为,解得,即点,
设点,则,
因为,则,可得,且,可得,
所以,点,
因为平面,、平面,,,
且,
所以,.
故答案为:.
【典例2】(23-24高二上·辽宁大连·期中)已知四棱锥P-ABCD的底面是边长为2的正方形,△PAD是以AD为斜边的等腰直角三角形,AB⊥平面PAD,E是线段PD上的动点(不含端点),若线段AB上存在点F(不含端点),使得异面直线PA和EF所成的角的大小为30°,则线段AF长的取值范围是 .
【答案】
【分析】建立空间直角坐标系,利用向量法列方程,结合二次函数的性质求得长的取值范围.
【详解】设是的中点,则,
由于平面,平面,所以,
由于平面,所以平面,
由于平面,所以平面平面,
以为原点建立如图所示空间直角坐标系,
,,
设;设,
则,
设与所成角为,则,
,
整理得,
函数的开口向下,对称轴为,
已知为直线上一点,且与不重合,若异面直线与所成角为余弦值为,则 .
【答案】
【分析】连接、交于点,以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,设,其中,利用空间向量法可得出关于实数的方程,结合可求得结果.
【详解】连接、交于点,则,
因为四棱锥为正四棱锥,故底面,
以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,
则、、、,
设,其中,
,则,
,由已知可得,
整理可得,因为,解得,即.
故答案为:
【变式3】(23-24高二上·吉林通化·期末)如图,在正四棱锥中,二面角为60°,E为的中点.已知F为直线上一点,且F与A不重合,若异面直线与所成角为60°,则= .
【答案】11
【分析】由题意建立空间直角坐标系,由二面角的定义得出,从而写出的坐标,由向量共线的性质设,利用向量的加法得出,由异面直线与所成角,利用向量法得出的值,从而得出的值.
【详解】取的中点G,与的交点为,以O为坐标原点,分别以为轴的正方向,建立空间直角坐标系,设
因为二面角为60°,所以
则.
设,则
从而
整理得,解得(舍),
故.
故答案为:
【点睛】本题主要考查了已知面面角,线线角求参数,属于中档题.
题型05易错题型求异面直线所成角忽略角的取值范围
【典例1】(23-24高二上·辽宁·期末)直三棱柱中,,则直线
,,
又两条异面所成的角为,则,
故选:B.
【变式2】(23-24高二上·山东枣庄·阶段练习)如图,在四棱锥中,底面为正方形,底面,,E为上一点,且,则异面直线与所成角的余弦值为( )
A. B. C. D.
【答案】B
【分析】以为坐标原点,以所在直线分别为轴,建立空间直角坐标系,利用向量夹角公式求解.
【详解】以为坐标原点,以所在直线分别为轴,建立空间直角坐标系,
设,则,
,
,
则异面直线与所成角的余弦值为.
故选:B.
21世纪教育网(www.21cnjy.com)
1、(传统法)核心技巧:平移使相交
具体操作,通过平移一条(或2条),使异面直线转化为相交直线,然后在三角形中利用余弦定理求角
2、(向量法)用向量运算求两条直线所成角
已知,为两异面直线,,与,分别是,上的任意两点,,所成的角为,则
①
②.
题型01求异面直线所成角(定值)(传统法)
【典例1】(23-24高一下·山东烟台·阶段练习)已知在长方体中,,直线与平面所成角的正弦值为为线段的中点,则直线与直线所成角的余弦值为( )
A. B. C. D.
【典例2】(23-24高一下·浙江·阶段练习)在正三棱柱中,面ABC,,则异面直线与所成角的余弦值为( )
A. B. C. D.
【变式1】(2024·重庆·模拟预测)如图,已知四边形是平行四边形,分别是的中点,点P在平面内的射影为与平面所成角的正切值为2,则直线与所成角的余弦值为( )
题型02求异面直线所成角(定值)(向量法)
【典例1】(2024·辽宁沈阳·模拟预测)已知直三棱柱中,,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
【典例2】(23-24高三上·广西·开学考试)正多面体被古希腊圣哲认为是构成宇宙的基本元素,加上它们的多种变体,一直是科学、艺术、哲学灵感的源泉之一.如图,该几何体是一个高为4的正八面体,G为的中点,则异面直线与所成角的正弦值为 .
【典例3】(2024高一下·全国·专题练习)如图,已知是圆柱下底面圆的圆心,为圆柱的一条母线,为圆柱下底面圆周上一点,,,为等腰直角三角形,则异面直线与所成角的余弦值为 .
【变式1】(2024·湖北武汉·模拟预测)已知菱形,,将沿对角线折起,使以四点为顶点的三棱锥体积最大,则异面直线与所成角的余弦值为( )
A. B. C. D.
【变式2】(23-24高三下·四川德阳·期末)正四面体中,、分别是和的中点,则和所成角的大小是 .
【变式3】(23-24高二上·广东茂名·期末)长方体中,,,点F是底面的中心,则直线与直线所成角的余弦值为 .
题型03求异面直线所成角(最值或范围)
【典例1】(23-24高二下·山东烟台·阶段练习)如图,在边长为1的正方体中,点在上,点在平面内,设直线与直线所成角为.若直线到平面的距离为,则的最小值为 .
【典例2】(23-24高二上·浙江金华·阶段练习)如图,在多面体中,平面,平面平面,是边长为的等边三角形,,.
(1)求点B到平面的距离;
(2)若M为的中点,N为线段上的动点,设异面直线与所成角为,求的最大值及此时的值
【变式3】(23-24高二上·吉林通化·期末)如图,在正四棱锥中,二面角为60°,E为的中点.已知F为直线上一点,且F与A不重合,若异面直线与所成角为60°,则= .
题型05易错题型求异面直线所成角忽略角的取值范围
【典例1】(23-24高二上·辽宁·期末)直三棱柱中,,则直线与夹角的余弦是( )
A. B. C. D.
【典例2】(23-24高二上·黑龙江齐齐哈尔·期末)中国古代数学瑰宝《九章算术》中记载了一种称为“曲池”的几何体,该几何体为上下底面均为扇环形的柱体(扇环是指圆环被扇形截得的部分).现有一个如图所示的曲池,其中底面,底面扇环所对的圆心角为,扇环对应的两个圆的半径之比为1∶2,在上且为靠近的三等分点,则异面直线与所成角的余弦值为( )
A. B. C. D.
【变式1】(23-24高二上·湖北武汉·期末)已知两条异面直线的方向向量分别是,则这两条异面直线所成的角满足( )
A. B.
C. D.
【变式2】(23-24高二上·山东枣庄·阶段练习)如图,在四棱锥中,底面为正方形,底面,,E为上一点,且,则异面直线与所成角的余弦值为( )
A. B. C. D.
21世纪教育网(www.21cnjy.com)
第07讲 拓展一:异面直线所成角(传统法与向量法)
1、(传统法)核心技巧:平移使相交
具体操作,通过平移一条(或2条),使异面直线转化为相交直线,然后在三角形中利用余弦定理求角
2、(向量法)用向量运算求两条直线所成角
已知,为两异面直线,,与,分别是,上的任意两点,,所成的角为,则
①
②.
题型01求异面直线所成角(定值)(传统法)
【典例1】(23-24高一下·山东烟台·阶段练习)已知在长方体中,,直线与平面所成角的正弦值为为线段的中点,则直线与直线所成角的余弦值为( )
A. B. C. D.
【答案】A
【分析】结合条件根据线面角的定义求得,连接,根据异面直线夹角的定义,利用余弦定理求解即可.
【详解】连接,因为平面,所以为直线与平面所成角,
设,则,
所以,所以,
连接连接,由长方体的性质知,且,
所以四边形为平行四边形,
所以,则或其补角即为直线与直线所成角,
在中,,
所以由余弦定理得,
即直线与直线所成角的余弦值为.
故选:A
【典例2】(23-24高一下·浙江·阶段练习)在正三棱柱中,面ABC,,则异面直线与所成角的余弦值为( )
A. B. C. D.
【答案】A
【分析】分别取的中点,可得是异面直线与所成角即为与所成角(或其补角),在中,由余弦定理求解即可.
【详解】分别取的中点,
连接,所以,
所以异面直线与所成角即为与所成角(或其补角),
即,设,所以,
,
所以在中,所以,
所以异面直线与所成角的余弦值为.
故选:A.
【变式1】(2024·重庆·模拟预测)如图,已知四边形是平行四边形,分别是的中点,点P在平面内的射影为与平面所成角的正切值为2,则直线与所成角的余弦值为( )
A. B. C. D.
【答案】A
【分析】根据题意,由条件可证,则直线与所成的角为,然后结合条件以及余弦定理代入计算,即可得到结果.
【详解】
如图,取的中点E,连接.因为分别是的中点,
所以.
因为四边形是平行四边形,所以.
因为N为的中点,所以,所以.
故四边形为平行四边形,所以,
所以直线与所成的角为.
连接,因为点P在平面内的射影为N,所以平面,
所以与平面所成的角为,所以.
不妨令,则,所以,
所以,
在中,
由余弦定理得.
故选:A.
【变式2】(23-24高一下·安徽阜阳·期中)如图,在正方体中,M,N分别为C1D1和CC1的中点,则异面直线AM与BN所成角的余弦值为( )
A. B. C. D.
【答案】A
【分析】分别为的中点,或其补角为AM与BN所成的角,设正方体的边长为,余弦定理求解即可.
【详解】取AB的中点,的中点,连接,
又M,N分别为和的中点,正方体中,,,
四边形为平行四边形,有,
同理有,则或其补角为AM与BN所成的角,
连接EF,设正方体的边长为,则,
,,
所以,
即异面直线AM与BN所成角的余弦值为.
故选:A.
【变式3】(23-24高三上·河南鹤壁·期中)如图,在正三棱柱中,,,则直线与直线所成角的正切值为 .
【答案】/
【分析】根据给定条件,作出直线与直线所成的角,再借助余弦定理求出余弦值即可求解.
【详解】在正三棱柱中,连接交于O点,取的中点F,连接OF,
显然是的中点,则,是与所成的角或其补角,
在中,,,,
,,
所以直线与直线所成角的正切值为.
故答案为:
【变式4】(2024·全国·模拟预测)在三棱锥中,,,,为的中点,则异面直线与所成角的余弦值是 .
【答案】
【分析】先根据异面直线所成角的定义确定为异面直线与所成的角或其补角;再根据勾股定理求出,余弦定理求出.,进而得出;最后在中,利用余弦定理即可求出.
【详解】取的中点,连接,如图所示:
因为为的中点,为的中点,
则根据三角形的中位线定理可得,且.
所以为异面直线与所成的角或其补角.
因为在中,,,,
所以,则.
又,所以.
又在中,,,
所以由余弦定理可得:.
又因为在中,,
所以由余弦定理可得:.
则在中,由余弦定理可得,,
所以异面直线与所成角的余弦值为.
故答案为:.
题型02求异面直线所成角(定值)(向量法)
【典例1】(2024·辽宁沈阳·模拟预测)已知直三棱柱中,,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
【答案】C
【分析】根据空间向量法求线线角解决即可.
【详解】以为原点,在平面过作的垂线交于,
以为轴,以为轴,以为轴,建立空间直角坐标系,
因为直三棱柱中,,,,
所以,
所以,
设异面直线与所成角为,
所以.
故选:C.
【典例2】(23-24高三上·广西·开学考试)正多面体被古希腊圣哲认为是构成宇宙的基本元素,加上它们的多种变体,一直是科学、艺术、哲学灵感的源泉之一.如图,该几何体是一个高为4的正八面体,G为的中点,则异面直线与所成角的正弦值为 .
【答案】
【分析】依题意,求出棱长,建立空间直角坐标系,借助向量求出异面直线夹角的余弦值,再转换为正弦值即可.
【详解】
连接交于点,连接,
因为该几何体是一个高为4的正八面体,
所以,,,
设棱长为,则,,
所以在中,,即,解得,
以所在直线为轴,建立如图所示空间直角坐标系,
则,
所以,
设异面直线与夹角为,
则,
因为,
所以异面直线与所成角的正弦值,
故答案为:.
【典例3】(2024高一下·全国·专题练习)如图,已知是圆柱下底面圆的圆心,为圆柱的一条母线,为圆柱下底面圆周上一点,,,为等腰直角三角形,则异面直线与所成角的余弦值为 .
【答案】
【分析】可借助等角定理得到或其补角即异面直线与所成的角,结合余弦定理计算;或借助空间向量的线性运算得到,再利用夹角公式计算.
【详解】方法一 :
如图,过点作交圆柱的上底面于点,连接,,
则由圆柱的性质易证四边形为矩形,所以,
所以或其补角即异面直线与所成的角,
在中,,所以,
因为为等腰直角三角形,且,所以,
所以,又,
所以,
即异面直线与所成角的余弦值为.
方法二 :
在中,,
所以,,
因为为等腰直角三角形,且,所以,
易知,所以,,,
所以,
所以,
则异面直线与所成角的余弦值为.
故答案为:.
【变式1】(2024·湖北武汉·模拟预测)已知菱形,,将沿对角线折起,使以四点为顶点的三棱锥体积最大,则异面直线与所成角的余弦值为( )
A. B. C. D.
【答案】C
【分析】当三棱锥的体积最大时,平面平面,以E为原点,分别为轴的正方向建立空间直角坐标系,求出向量的坐标,根据向量夹角的坐标表示可解.
【详解】记的 中点分别为,因为,所以,
同理,,记,
因为,所以,
所以,,
易知,当平面平面时,三棱锥的体积最大,此时,
以E为原点,分别为轴的正方向建立空间直角坐标系,
则
所以,
所以,
所以异面直线与所成角的余弦值为.
故选:C
【变式2】(23-24高三下·四川德阳·期末)正四面体中,、分别是和的中点,则和所成角的大小是 .
【答案】/
【分析】构造辅助线,利用中位线定理得到是和所成角,然后结合向量数量积的变形即可求解.
【详解】取中点,连接,令棱长为,
因为、分别是和的中点,
所以,,,,
所以是和所成角,
又,
,
,
所以 ,
,,
所以,
所以,即和所成角的大小为.
故答案为:
【变式3】(23-24高二上·广东茂名·期末)长方体中,,,点F是底面的中心,则直线与直线所成角的余弦值为 .
【答案】/
【分析】建立空间直角坐标系,利用坐标进行计算即可.
【详解】如图所示,建立如下空间直角坐标系,
依题可得,,
则,
所以,
故直线与直线所成角的余弦值为,
故答案为:.
题型03求异面直线所成角(最值或范围)
【典例1】(23-24高二下·山东烟台·阶段练习)如图,在边长为1的正方体中,点在上,点在平面内,设直线与直线所成角为.若直线到平面的距离为,则的最小值为 .
【答案】
【分析】建立空间直角坐标系,利用向量法表示出到面的距离,进而求出点坐标,过作平面的平行平面,得到点的轨迹,再利用向量法求线线角,进而求其最值即可.
【详解】因为直线到平面的距离为,
所以必有面,即点到平面的距离为,
如图建立空间直角坐标系,设,又,
则,
设面的法向量为,
则,取得,
则,解得,即,
过作平面的平行平面,与正方体的截面为,
分别为线段和线段的中点,则
所以在直线上,
设,
又,则,
当时,,
当时,,
又,所以,
则的最小值为.
故答案为:
【典例2】(23-24高二上·浙江金华·阶段练习)如图,在多面体中,平面,平面平面,是边长为的等边三角形,,.
(1)求点B到平面的距离;
(2)若M为的中点,N为线段上的动点,设异面直线与所成角为,求的最大值及此时的值
【答案】(1)
(2);
【分析】
(1)说明两两垂直,建立空间直角坐标系,求出相关点的坐标,求出平面的法向量,根据空间距离的向量求法,即可求得答案;
(2)设,表示出N点坐标,即可求得坐标,结合的坐标,根据空间角的向量求法,即可求得的最大值及此时的值.
【详解】(1)设的中点为O,连接,而,则,
是边长为的等边三角形,故,则,
平面平面,平面平面,平面,
故平面,平面,故,
又是边长为的等边三角形,的中点为O,故,
故以所在直线为轴,建立空间直角坐标系,
则,
,
设平面的一个法向量为,则,
令,则,又,
故点B到平面的距离为;
(2)M为的中点,即为O点;
N为线段上的动点,设,
而,即,故点,
故,而,
设异面直线与所成角为,则
,
令,则,
故,
令,则,即为,
当时,取得最小值,
即,即时,取得最大值,
即的最大值为,此时的值为.
【典例3】(23-24高三下·湖南长沙·开学考试)三棱锥中,平面,,.,点是面内的动点(不含边界),,则异面直线与所成角的余弦值的取值范围为( )
A. B. C. D.
【答案】A
【分析】建立空间直角坐标系,由,可得,再利用线线角的向量求法求解即得.
【详解】由平面平面,得,
又平面,则平面,
平面,则,又,平面,
因此平面,而平面,则,
如图,以为坐标原点,的方向为轴正方向建立空间直角坐标系,
则,设,
,由,得,
,设异面直线与所成角为,
则,
令,则,
显然函数在上单调递增,此时,,
所以异面直线与所成角的余弦值的取值范围为.
故选:A
【点睛】思路点睛:求空间角余弦的最值或范围问题,根据给定条件,选定变量,将该角的余弦建立起变量的函数,求出函数最值或范围即可.
【变式1】(23-24高二上·山东潍坊·期末)在直三棱柱中,,,平面经过点A,且直线与平面所成的角为30°,过点作平面的垂线,垂足为H,则点到平面的距离为 ,直线与BH所成角的范围为 .
【答案】 2
【分析】利用,得出在以为直径的球面上,其时可得出到平面的距离,由直线与平面所成的角为30°,得在以为轴,顶角为的圆锥面上,从而得出的轨迹是圆,然后建立如图所示的空间直角坐标系,利用空间向量法求得与所成角的余弦值,角的范围.
【详解】如图,连接,因为,,所以,
所以在以为直径的球面上,又直线与平面所成角为,而即为直线与平面所成的角,因此,因此在以为轴,顶角为的圆锥面上,
过作于点,则,其中的长即为到平面的距离.
所以在圆锥的底面圆上,为圆心,半径为,
以为轴,为轴,过与垂直的直线的为轴建立如图所示的空间直角坐标系,
则,设,
,取的一个方向向量为,
,
又,所以,
所以直线与所成角的范围是,即,
故答案为:;.
【变式2】(23-24高二上·黑龙江哈尔滨·期末)如图,在长方体中,E是的中点,点F是AD上一点,,,,动点P在上底面上,且满足三棱锥的体积等于1,则直线CP与所成角的余弦值的最大值为 .
【答案】/
【分析】建立空间直角坐标系,设,通过向量法算出点P到平面BFE的距离,结合三棱锥的体积等于1可得到,再通过向量法计算直线CP与所成角的余弦值的范围,继而算出答案
【详解】以D为坐标原点,分别以所在直线为x,y,z轴建立空间直角坐标系,
,则,,
,
设平面的法向量为,则,令,得,
而,则点P到平面BFE的距离,
又,
在等腰中,到的高为,则
而,于是,
解得或,由,得,则,
设直线与所成的角为,则,,
,当且仅当时取等号,
所以的最大值为,
故答案为:
【点睛】方法点睛:求点到平面的距离可以利用几何法,作出点到平面的垂线段求解;也可以用向量法,求出平面的法向量,再求出这一点与平面内任意一点确定的向量在法向量的投影即可.
【变式3】(23-24高二上·河南洛阳·期中)如图,四边形和均为正方形,且,平面平面分别为的中点,为线段上的动点,则异面直线与所成角的余弦值最大时, .
【答案】
【分析】根据题意建立空间直角坐标系,求出异面直线与所成角的余弦值最大时点位置,进而求出大小.
【详解】
由题可以为原点,建立空间直角坐标系如图所示:
则,设,
则,
设异面直线与所成角为,
则,
令,
则,
当时,,
当时,,
令,则,
因为,
当时,有最小值,
此时有最大值,
由得,,
则异面直线与所成角的余弦值最大时,
即,,
所以.
故答案为:
题型04已知线线角求参数
【典例1】(23-24高三上·河北唐山·期末)如图,在四棱柱中,底面,且底面为菱形,,,,为的中点,在上,在平面内运动(不与重合),且平面,异面直线与所成角的余弦值为,则的最大值为 .
【答案】/
【分析】连接交于点,推导出平面,然后以点为坐标原点,、、的方向分别为、、轴的正方向建立空间直角坐标系,设,其中,利用空间向量法可求得的值,求出点的坐标为,求出的最小值,即可求得的最大值.
【详解】连接交于点,平面,平面,则,
因为四边形为菱形,则,
,、平面,平面,
以点为坐标原点,、、的方向分别为、、轴的正方向建立如下图所示的空间直角坐标系,
则、、、、、、,
易知平面的一个法向量为,
因为平面,所以,,
设点,其中,则,
由已知可得,
因为,解得,即点,
设点,则,
因为,则,可得,且,可得,
所以,点,
因为平面,、平面,,,
且,
所以,.
故答案为:.
【典例2】(23-24高二上·辽宁大连·期中)已知四棱锥P-ABCD的底面是边长为2的正方形,△PAD是以AD为斜边的等腰直角三角形,AB⊥平面PAD,E是线段PD上的动点(不含端点),若线段AB上存在点F(不含端点),使得异面直线PA和EF所成的角的大小为30°,则线段AF长的取值范围是 .
【答案】
【分析】建立空间直角坐标系,利用向量法列方程,结合二次函数的性质求得长的取值范围.
【详解】设是的中点,则,
由于平面,平面,所以,
由于平面,所以平面,
由于平面,所以平面平面,
以为原点建立如图所示空间直角坐标系,
,,
设;设,
则,
设与所成角为,则,
,
整理得,
函数的开口向下,对称轴为,
已知为直线上一点,且与不重合,若异面直线与所成角为余弦值为,则 .
【答案】
【分析】连接、交于点,以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,设,其中,利用空间向量法可得出关于实数的方程,结合可求得结果.
【详解】连接、交于点,则,
因为四棱锥为正四棱锥,故底面,
以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,
则、、、,
设,其中,
,则,
,由已知可得,
整理可得,因为,解得,即.
故答案为:
【变式3】(23-24高二上·吉林通化·期末)如图,在正四棱锥中,二面角为60°,E为的中点.已知F为直线上一点,且F与A不重合,若异面直线与所成角为60°,则= .
【答案】11
【分析】由题意建立空间直角坐标系,由二面角的定义得出,从而写出的坐标,由向量共线的性质设,利用向量的加法得出,由异面直线与所成角,利用向量法得出的值,从而得出的值.
【详解】取的中点G,与的交点为,以O为坐标原点,分别以为轴的正方向,建立空间直角坐标系,设
因为二面角为60°,所以
则.
设,则
从而
整理得,解得(舍),
故.
故答案为:
【点睛】本题主要考查了已知面面角,线线角求参数,属于中档题.
题型05易错题型求异面直线所成角忽略角的取值范围
【典例1】(23-24高二上·辽宁·期末)直三棱柱中,,则直线
,,
又两条异面所成的角为,则,
故选:B.
【变式2】(23-24高二上·山东枣庄·阶段练习)如图,在四棱锥中,底面为正方形,底面,,E为上一点,且,则异面直线与所成角的余弦值为( )
A. B. C. D.
【答案】B
【分析】以为坐标原点,以所在直线分别为轴,建立空间直角坐标系,利用向量夹角公式求解.
【详解】以为坐标原点,以所在直线分别为轴,建立空间直角坐标系,
设,则,
,
,
则异面直线与所成角的余弦值为.
故选:B.
21世纪教育网(www.21cnjy.com)
