江苏省徐州市邳州市戴庄中学2024-2025学年九年级上学期数学第一次学情检测试卷(无答案)
文档属性
| 名称 | 江苏省徐州市邳州市戴庄中学2024-2025学年九年级上学期数学第一次学情检测试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 151.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-08 16:27:40 | ||
图片预览

文档简介
(
……………………………………密……………………………………封……………………………………线………………………………………
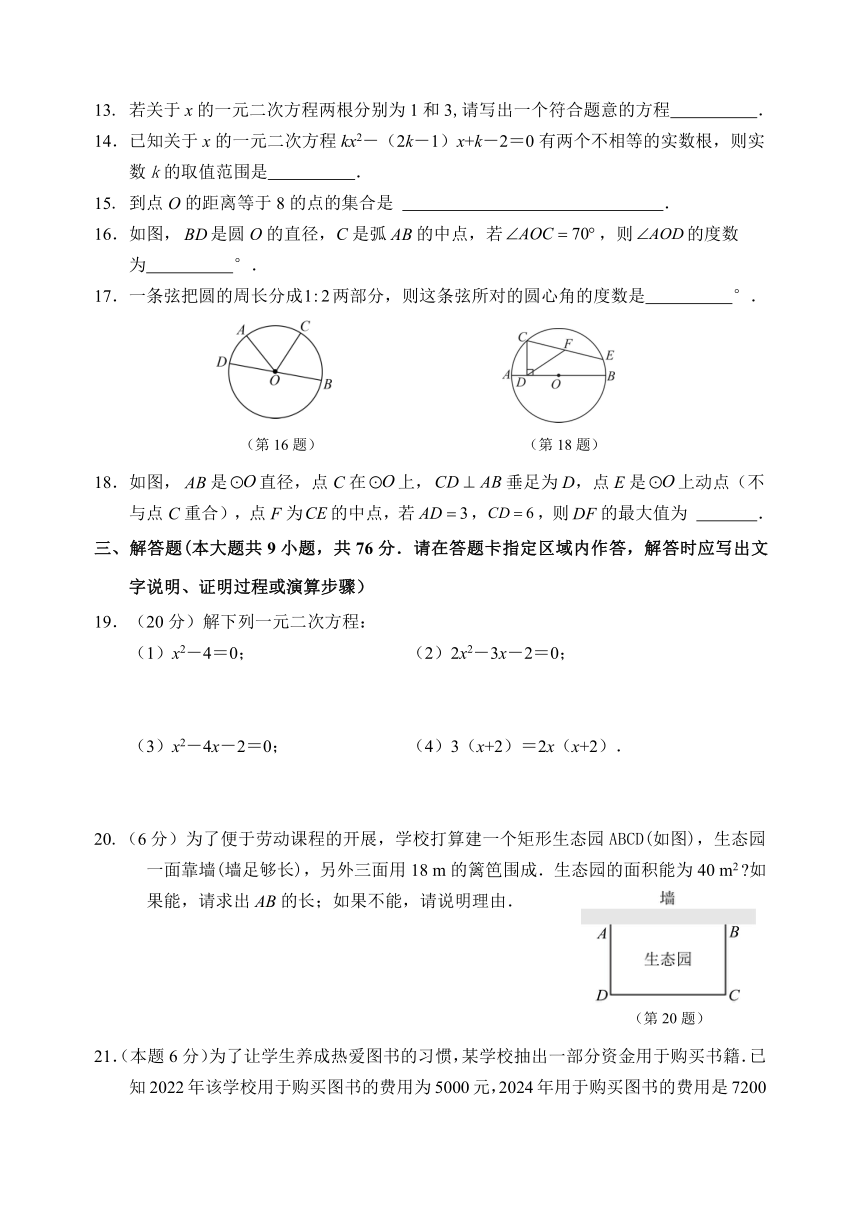
学
校
班
级
____________
姓
名
得分
)2024~2025学年度第一学期九年级学情调研数学试题
一、选择题(本大题共8小题,每小题4分,共32分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置)
1.下列方程中,属于一元二次方程的是( )
A. B. C. D.
2.把一元二次方程2x(x-1)=(x-3)+4化成一般形式之后,其二次项系数与一次项分别( )
A. 2、-3 B. -2、-3 C. 2、-3x D. -2、-3x
3.用配方法解一元二次方程x2-6x+8=0配方后得到的方程是( )
A.(x+6)2=28 B.(x-6)2=28 C.(x+3)2=1 D.(x-3)2=1
4.若关于x的方程x2+mx+1=0有两个不相等的实数根,则m的值可以是( )
A. 0 B. -1 C. 2 D. -3
5.若n(n≠0)是关于x的方程x2+mx+2n=0的根,则m+n的值为( )
A. -2 B. -1 C. 1 D. 2
6. 某地区2021年人均可支配收入为26000元,2023年人均可支配收入为31000元.设该地区2021年至2023年居民人均可支配收入的年平均增长率为x,则可列方程为( )
A. 26000(1+2x)=31000 B. 26000(1+x)2=31000
C. 26000(1-2x)=31000 D. 26000(1-x)2=31000
7.已知☉O的直径为10cm,点P到圆心O的距离为8cm,则点P和圆的位置关系( )
A. 点P在圆内 B. 点P在圆外
C. 点P在圆上 D. 无法判断
8.下列说法中,正确的个数为( )
①面积相等的圆是等圆;②过圆心的线段是直径; ③长度相等的弧是等弧;④半径是弦;⑤直径是最长的弦;⑥等弧所在的圆一定是等圆或同圆,
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共10小题,每小题4分,共40分.不需写出解答过程,请将答案直接填写在答题卡相应位置)
9.一元二次方程的解是 .
10.关于x的方程是一元二次方程,则m= .
11.已知m为方程 的一个根,则代数式的值是 .
12. 若x1,x2是一元二次方程x2+5x-1=0的两个实数根,则x1+x2的值为 .
13. 若关于x的一元二次方程两根分别为1和3,请写出一个符合题意的方程 .
14.已知关于x的一元二次方程kx2-(2k-1)x+k-2=0有两个不相等的实数根,则实数k的取值范围是 .
15. 到点O的距离等于8的点的集合是 .
16.如图,是圆O的直径,C是弧的中点,若,则的度数为 °.
17.一条弦把圆的周长分成两部分,则这条弦所对的圆心角的度数是 °.
(
(第
16
题)
(第
18
题)
)
18.如图,是直径,点C在上,垂足为D,点E是上动点(不与点C重合),点F为的中点,若,,则的最大值为 .
三、解答题(本大题共9小题,共76分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
19.(20分)解下列一元二次方程:
(1)x2-4=0; (2)2x2-3x-2=0;
(3)x2-4x-2=0; (4)3(x+2)=2x(x+2).
(
(
第
20
题)
)20.(6分)为了便于劳动课程的开展,学校打算建一个矩形生态园ABCD(如图),生态园一面靠墙(墙足够长),另外三面用18 m的篱笆围成.生态园的面积能为40 m2 如果能,请求出AB的长;如果不能,请说明理由.
21.(本题6分)为了让学生养成热爱图书的习惯,某学校抽出一部分资金用于购买书籍.已知2022年该学校用于购买图书的费用为5000元,2024年用于购买图书的费用是7200元,求2022至2024年买书资金的平均增长率.
22.(本题6分)已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)若x=1是方程的一个根,求实数m的值;
(2)求证:方程总有两个不相等的实数根.
23.(本题7分)如图,在宽为20 m,长为32 m的矩形耕地上,修筑同样宽的三条道路,把耕地分成大小相等的六块作试验田,要使试验田面积为570 m2,求道路的宽度.
(
(第
23
题)
)
24.(本题8分)某商品现在的售价为每件60元,每星期可卖出300件. 市场调查反映:每降价0.5元,每星期可多卖出10件. 已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6080元的利润,应将销售单价定为多少元
(
(第
25
题)
)25.(本题8分)饮食文化源远流长,“老碗面”是陕西地方特色美食之一.图②是从正面看到的一个“老碗”( 图①)的形状示意图.是⊙O的一部分,D是的中点,连接OD,与弦AB交于点C,连接OA,OB.已知AB=24 cm,碗深CD=8 cm,求⊙O的半径OA.
26.(本题12分)如图所示,四边形ABCD为矩形,AB=6 cm,AD=4 cm,若点Q从A点出发沿AD以1 cm/s的速度向D运动,P从B点出发沿BA以2 cm/s的速度向A运动,如果P、Q分别同时出发,当一个点到达终点时,另一点也同时停止.设运动的时间为t s.
(1)当t为何值时,△PAQ为等腰三角形?
(2)当t为何值时,△APD的面积为6 cm2?
(3)五边形PBCDQ的面积能否达到20 cm2?若能,请求出t的值;若不能,请说明理由.
(
(第
26
题)
)
……………………………………密……………………………………封……………………………………线………………………………………
学
校
班
级
____________
姓
名
得分
)2024~2025学年度第一学期九年级学情调研数学试题
一、选择题(本大题共8小题,每小题4分,共32分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置)
1.下列方程中,属于一元二次方程的是( )
A. B. C. D.
2.把一元二次方程2x(x-1)=(x-3)+4化成一般形式之后,其二次项系数与一次项分别( )
A. 2、-3 B. -2、-3 C. 2、-3x D. -2、-3x
3.用配方法解一元二次方程x2-6x+8=0配方后得到的方程是( )
A.(x+6)2=28 B.(x-6)2=28 C.(x+3)2=1 D.(x-3)2=1
4.若关于x的方程x2+mx+1=0有两个不相等的实数根,则m的值可以是( )
A. 0 B. -1 C. 2 D. -3
5.若n(n≠0)是关于x的方程x2+mx+2n=0的根,则m+n的值为( )
A. -2 B. -1 C. 1 D. 2
6. 某地区2021年人均可支配收入为26000元,2023年人均可支配收入为31000元.设该地区2021年至2023年居民人均可支配收入的年平均增长率为x,则可列方程为( )
A. 26000(1+2x)=31000 B. 26000(1+x)2=31000
C. 26000(1-2x)=31000 D. 26000(1-x)2=31000
7.已知☉O的直径为10cm,点P到圆心O的距离为8cm,则点P和圆的位置关系( )
A. 点P在圆内 B. 点P在圆外
C. 点P在圆上 D. 无法判断
8.下列说法中,正确的个数为( )
①面积相等的圆是等圆;②过圆心的线段是直径; ③长度相等的弧是等弧;④半径是弦;⑤直径是最长的弦;⑥等弧所在的圆一定是等圆或同圆,
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共10小题,每小题4分,共40分.不需写出解答过程,请将答案直接填写在答题卡相应位置)
9.一元二次方程的解是 .
10.关于x的方程是一元二次方程,则m= .
11.已知m为方程 的一个根,则代数式的值是 .
12. 若x1,x2是一元二次方程x2+5x-1=0的两个实数根,则x1+x2的值为 .
13. 若关于x的一元二次方程两根分别为1和3,请写出一个符合题意的方程 .
14.已知关于x的一元二次方程kx2-(2k-1)x+k-2=0有两个不相等的实数根,则实数k的取值范围是 .
15. 到点O的距离等于8的点的集合是 .
16.如图,是圆O的直径,C是弧的中点,若,则的度数为 °.
17.一条弦把圆的周长分成两部分,则这条弦所对的圆心角的度数是 °.
(
(第
16
题)
(第
18
题)
)
18.如图,是直径,点C在上,垂足为D,点E是上动点(不与点C重合),点F为的中点,若,,则的最大值为 .
三、解答题(本大题共9小题,共76分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
19.(20分)解下列一元二次方程:
(1)x2-4=0; (2)2x2-3x-2=0;
(3)x2-4x-2=0; (4)3(x+2)=2x(x+2).
(
(
第
20
题)
)20.(6分)为了便于劳动课程的开展,学校打算建一个矩形生态园ABCD(如图),生态园一面靠墙(墙足够长),另外三面用18 m的篱笆围成.生态园的面积能为40 m2 如果能,请求出AB的长;如果不能,请说明理由.
21.(本题6分)为了让学生养成热爱图书的习惯,某学校抽出一部分资金用于购买书籍.已知2022年该学校用于购买图书的费用为5000元,2024年用于购买图书的费用是7200元,求2022至2024年买书资金的平均增长率.
22.(本题6分)已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)若x=1是方程的一个根,求实数m的值;
(2)求证:方程总有两个不相等的实数根.
23.(本题7分)如图,在宽为20 m,长为32 m的矩形耕地上,修筑同样宽的三条道路,把耕地分成大小相等的六块作试验田,要使试验田面积为570 m2,求道路的宽度.
(
(第
23
题)
)
24.(本题8分)某商品现在的售价为每件60元,每星期可卖出300件. 市场调查反映:每降价0.5元,每星期可多卖出10件. 已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6080元的利润,应将销售单价定为多少元
(
(第
25
题)
)25.(本题8分)饮食文化源远流长,“老碗面”是陕西地方特色美食之一.图②是从正面看到的一个“老碗”( 图①)的形状示意图.是⊙O的一部分,D是的中点,连接OD,与弦AB交于点C,连接OA,OB.已知AB=24 cm,碗深CD=8 cm,求⊙O的半径OA.
26.(本题12分)如图所示,四边形ABCD为矩形,AB=6 cm,AD=4 cm,若点Q从A点出发沿AD以1 cm/s的速度向D运动,P从B点出发沿BA以2 cm/s的速度向A运动,如果P、Q分别同时出发,当一个点到达终点时,另一点也同时停止.设运动的时间为t s.
(1)当t为何值时,△PAQ为等腰三角形?
(2)当t为何值时,△APD的面积为6 cm2?
(3)五边形PBCDQ的面积能否达到20 cm2?若能,请求出t的值;若不能,请说明理由.
(
(第
26
题)
)
同课章节目录
