湘教版数学九年级上册(新)导学案:4.1.1 《正弦》(无答案)
文档属性
| 名称 | 湘教版数学九年级上册(新)导学案:4.1.1 《正弦》(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 36.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-18 18:46:03 | ||
图片预览

文档简介
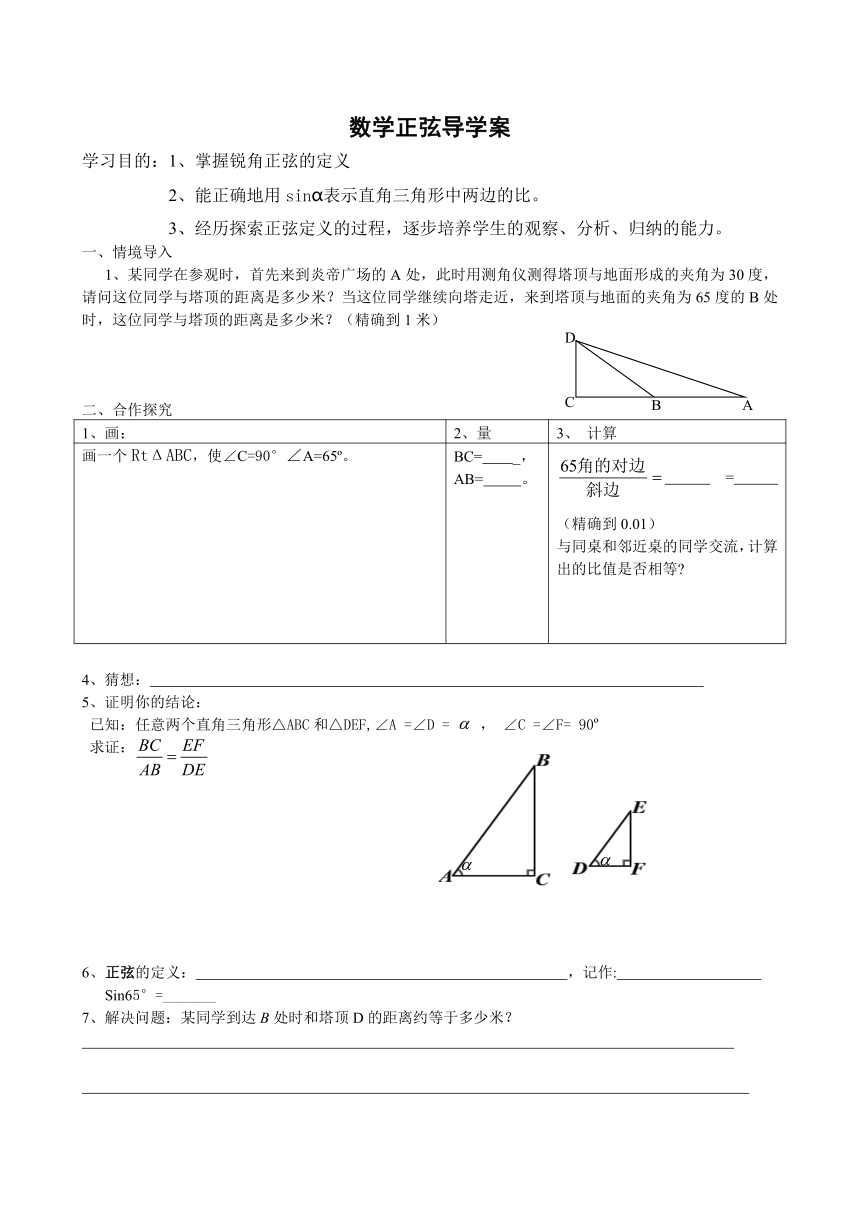
数学正弦导学案
学习目的:1、掌握锐角正弦的定义
2、能正确地用sinɑ表示直角三角形中两边的比。
3、经历探索正弦定义的过程,逐步培养学生的观察、分析、归纳的能力。
一、情境导入
1、某同学在参观时,首先来到炎帝广场的A ( http: / / www.21cnjy.com )处,此时用测角仪测得塔顶与地面形成的夹角为30度,请问这位同学与塔顶的距离是多少米?当这位同学继续向塔走近,来到塔顶与地面的夹角为65度的B处时,这位同学与塔顶的距离是多少米?(精确到1米)
二、合作探究
1、画: 2、量 3、 计算
画一个RtΔABC,使∠C=90°∠A=65 。 BC= _,AB= 。 = (精确到0.01)与同桌和邻近桌的同学交流,计算出的比值是否相等
4、猜想:
5、证明你的结论:
已知:任意两个直角三角形△ABC和△DEF,∠A =∠D = , ∠C =∠F= 90
求证:
6、正弦的定义: ,记作:
Sin65°=_______
7、解决问题:某同学到达B处时和塔顶D的距离约等于多少米?
三.典例精析:
例1:如图,在Rt△ABC中,∠C=90°,BC=3,AB=5. (1)求∠A的正弦sinA;(2)求∠B的正弦sinB。 例2.在Rt△ABC中, ∠C= 90 , BC=4,sinA =.(1)求AB的长;(2)求AC的长;
当堂检测:
1、RtΔABC中, AC=1,BC=1,则sinB= ,sinA= 。
2、RtΔABC中, AC=3,BC=4,则sinB= ,sinA= 。
3、 Rt△ABC中,∠C是直角,斜边AB是3,AC=2,则sinA=______,sinB=_______。
4、在直角三角形ABC中,若三边长都扩大2倍,则锐角A的正弦值( )
A、扩大2倍 B、不变 C、缩小2倍 D、无法确定。
5、在Rt△ABC中,∠C=90,sinB=,AB= cm,则AC= .
6、如图,Rt△ABC中,∠C=90°,BC=5,AB=13.求sinA 、sinB的值. 7.如图,在平面直角坐标系内有一点P(3,4)连接OP,求OP与x轴正方向所夹锐角ɑ的正弦值。
五、本节课你有什么收获 ?
六、拓展提升:小刚说:对于任意锐角α,都有0﹤sinɑ﹤1,你认为他说得对吗?为什么?
A
B
C
D
C
A
B
3
5
C
A
B
4
C
A
B
5
13
P(3,4)
学习目的:1、掌握锐角正弦的定义
2、能正确地用sinɑ表示直角三角形中两边的比。
3、经历探索正弦定义的过程,逐步培养学生的观察、分析、归纳的能力。
一、情境导入
1、某同学在参观时,首先来到炎帝广场的A ( http: / / www.21cnjy.com )处,此时用测角仪测得塔顶与地面形成的夹角为30度,请问这位同学与塔顶的距离是多少米?当这位同学继续向塔走近,来到塔顶与地面的夹角为65度的B处时,这位同学与塔顶的距离是多少米?(精确到1米)
二、合作探究
1、画: 2、量 3、 计算
画一个RtΔABC,使∠C=90°∠A=65 。 BC= _,AB= 。 = (精确到0.01)与同桌和邻近桌的同学交流,计算出的比值是否相等
4、猜想:
5、证明你的结论:
已知:任意两个直角三角形△ABC和△DEF,∠A =∠D = , ∠C =∠F= 90
求证:
6、正弦的定义: ,记作:
Sin65°=_______
7、解决问题:某同学到达B处时和塔顶D的距离约等于多少米?
三.典例精析:
例1:如图,在Rt△ABC中,∠C=90°,BC=3,AB=5. (1)求∠A的正弦sinA;(2)求∠B的正弦sinB。 例2.在Rt△ABC中, ∠C= 90 , BC=4,sinA =.(1)求AB的长;(2)求AC的长;
当堂检测:
1、RtΔABC中, AC=1,BC=1,则sinB= ,sinA= 。
2、RtΔABC中, AC=3,BC=4,则sinB= ,sinA= 。
3、 Rt△ABC中,∠C是直角,斜边AB是3,AC=2,则sinA=______,sinB=_______。
4、在直角三角形ABC中,若三边长都扩大2倍,则锐角A的正弦值( )
A、扩大2倍 B、不变 C、缩小2倍 D、无法确定。
5、在Rt△ABC中,∠C=90,sinB=,AB= cm,则AC= .
6、如图,Rt△ABC中,∠C=90°,BC=5,AB=13.求sinA 、sinB的值. 7.如图,在平面直角坐标系内有一点P(3,4)连接OP,求OP与x轴正方向所夹锐角ɑ的正弦值。
五、本节课你有什么收获 ?
六、拓展提升:小刚说:对于任意锐角α,都有0﹤sinɑ﹤1,你认为他说得对吗?为什么?
A
B
C
D
C
A
B
3
5
C
A
B
4
C
A
B
5
13
P(3,4)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
