22.1 二次函数y=ax2的图象和性质课件
文档属性
| 名称 | 22.1 二次函数y=ax2的图象和性质课件 |  | |
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-19 23:16:37 | ||
图片预览







文档简介
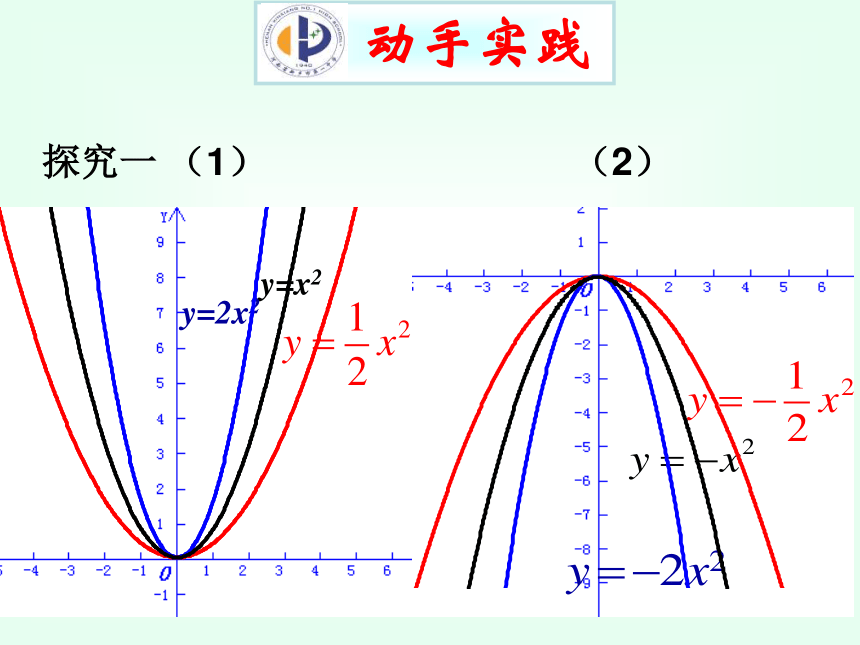
课件24张PPT。抛物线型弹头1.会用描点法画函数 的图象. 2.能够结合函数 的图象理解抛物线的有关 概念和探究函数的性质.学习重点:1.会画函数 的图象.2.能根据函数图象观察分析出二次函数 的 性质.3.在经历画函数图象、观察、分析、比较、归纳等探究活动中,体会蕴含的数学思想及方法. 学习目标列表描点连线画函数图象的一般步骤确定自变量的取值范围 温故知新用平滑曲线将点从左到右顺次连接(2)函数 的图象. 请你在所发的直角坐标纸中画出(1)函数 的图象.探究一 画函数图象 动手实践 动手实践 探究一 (1) (2)想一想:可以从哪些角度探究函数
的性质?开口方向对称性顶点坐标最值增减性 探索性质 探究二
分别找出探究一的(1)和(2)中所画图象的共同点和不同点,进而总结归纳出二次函数 和 的性质,并填写学案上的表格. 探索性质抛物线顶点坐标对称轴最高
(低)点开口方向增减性y的最值y=ax2 (a>0)y= ax2 (a<0)(0,0)(0,0)y轴y轴有最低点(0,0)有最高点(0,0)向上(向上无限延伸)向下(向下无限延伸)当x=0时,有最小值为y=0.当x=0时,有最大值为y=0.在对称轴的左侧(x≤0),
y随x的增大而减小.
在对称轴的右侧(x≥0),
y随x的增大而增大. 在对称轴的左侧(x≤0),
y随x的增大而增大.
在对称轴的右侧 (x≥0),
y随x的增大而减小. 开口大小a越大,开口越小a越小,开口越小1 归纳性质对比同颜色的函数图象 对比探究1. 抛物线 的顶点坐标是 ;
抛物线 的开口方向是 .(0,0)开口向下四① 图象是一条抛物线;② 图象是一条折线;③ 图象开口向上;④ 图象过点(0,0);⑤ 图象关于y轴对称;⑥ y随x的增大而增大.
一定正确的有( )
A、①③④⑥ B、②③④⑤
C、①④⑤ D、②③⑤⑥C1.你在本节课中学到了哪些数学知识?
2.你在本节课中领会到了哪些数学思想、
用到了哪些数学方法?
谈谈你的收获数形结合、类比、分类讨论、由特殊到一般.请课代表宣读优胜小组3.根据自己的能力选做训练案中的题目.(A 级是拔高题、B级是能力题、C级是基础题)提倡挑战自我.1.画出探究一中你在课上没有画的函数图象. 课堂作业 强大的国防力量只是中华民族快速发展的一个缩影,民族复兴的重任将由我们当代人承担.学好数学,提高探索和认识世界的能力是我们义不容辞的责任.让我们共同努力,实现中国梦! 结束寄语
的性质?开口方向对称性顶点坐标最值增减性 探索性质 探究二
分别找出探究一的(1)和(2)中所画图象的共同点和不同点,进而总结归纳出二次函数 和 的性质,并填写学案上的表格. 探索性质抛物线顶点坐标对称轴最高
(低)点开口方向增减性y的最值y=ax2 (a>0)y= ax2 (a<0)(0,0)(0,0)y轴y轴有最低点(0,0)有最高点(0,0)向上(向上无限延伸)向下(向下无限延伸)当x=0时,有最小值为y=0.当x=0时,有最大值为y=0.在对称轴的左侧(x≤0),
y随x的增大而减小.
在对称轴的右侧(x≥0),
y随x的增大而增大. 在对称轴的左侧(x≤0),
y随x的增大而增大.
在对称轴的右侧 (x≥0),
y随x的增大而减小. 开口大小a越大,开口越小a越小,开口越小1 归纳性质对比同颜色的函数图象 对比探究1. 抛物线 的顶点坐标是 ;
抛物线 的开口方向是 .(0,0)开口向下四① 图象是一条抛物线;② 图象是一条折线;③ 图象开口向上;④ 图象过点(0,0);⑤ 图象关于y轴对称;⑥ y随x的增大而增大.
一定正确的有( )
A、①③④⑥ B、②③④⑤
C、①④⑤ D、②③⑤⑥C1.你在本节课中学到了哪些数学知识?
2.你在本节课中领会到了哪些数学思想、
用到了哪些数学方法?
谈谈你的收获数形结合、类比、分类讨论、由特殊到一般.请课代表宣读优胜小组3.根据自己的能力选做训练案中的题目.(A 级是拔高题、B级是能力题、C级是基础题)提倡挑战自我.1.画出探究一中你在课上没有画的函数图象. 课堂作业 强大的国防力量只是中华民族快速发展的一个缩影,民族复兴的重任将由我们当代人承担.学好数学,提高探索和认识世界的能力是我们义不容辞的责任.让我们共同努力,实现中国梦! 结束寄语
同课章节目录
