高考数学考点题型归纳与方法总结(新高考)素养拓展29立体几何中的结构不良问题(学案+练习)
文档属性
| 名称 | 高考数学考点题型归纳与方法总结(新高考)素养拓展29立体几何中的结构不良问题(学案+练习) |  | |
| 格式 | docx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-08 18:07:52 | ||
图片预览




文档简介
2024年高考数学高频考点题型归纳与方法总结(新高考通用)
素养拓展29 立体几何中的结构不良问题(精讲+精练)
一、空间向量与立体几何的求解公式
(1)异面直线成角:设a,b分别是两异面直线l1,l2的方向向量,则l1与l2所成的角θ满足:cos θ=;
(2)线面成角:设直线l的方向向量为a,平面α的法向量为n,a与n的夹角为β,
则直线l与平面α所成的角为θ满足:sin θ=|cos β|=.
(9)二面角:设n1,n2分别是二面角α-l-β的两个半平面α,β的法向量,
则两面的成角θ满足:cos θ=cos〈n1,n2〉=;
注意:二面角的平面角大小是向量n1与n2的夹角或是向量n1与n2的夹角的补角,具体情况要判断确定.
(4)点到平面的距离:如右图所示,已知AB为平面α的一条斜线段,n为平面α的法向量,
则点B到平面α的距离为:||=,即向量在法向量n的方向上的投影长.
二、几种常见角的取值范围
①异面直线成角∈(0,] ;②二面角∈[0,π] ;③线面角∈[0,] ;④向量夹角∈[0,π]
三、平行构造的常用方法
①三角形中位线法;②平行四边形线法;③比例线段法.
四、垂直构造的常用方法
①等腰三角形三线合一法;②勾股定理法;③投影法.
五、用向量证明空间中的平行关系
(1)线线平行:设直线l1和l2的方向向量分别为v1和v2,则l1∥l2(或l1与l2重合) v1∥v2.
(2)线面平行:设直线l的方向向量为v,平面α的法向量为u,则l∥α或l α v⊥u.
(9)面面平行:设平面α和β的法向量分别为u1,u2,则α∥β u1 ∥u2.
六、用向量证明空间中的垂直关系
(1)线线垂直:设直线l1和l2的方向向量分别为v1和v2,则l1⊥l2 v1⊥v2 v1·v2=0.
(2)线面垂直:设直线l的方向向量为v,平面α的法向量为u,则l⊥α v∥u.
(9)面面垂直:设平面α和β的法向量分别为u1和u2,则α⊥β u1⊥u2 u1·u2=0.
七、点面距常用方法
①作点到面的垂线,点到垂足的距离即为点到平面的距离;②等体积法;③向量法
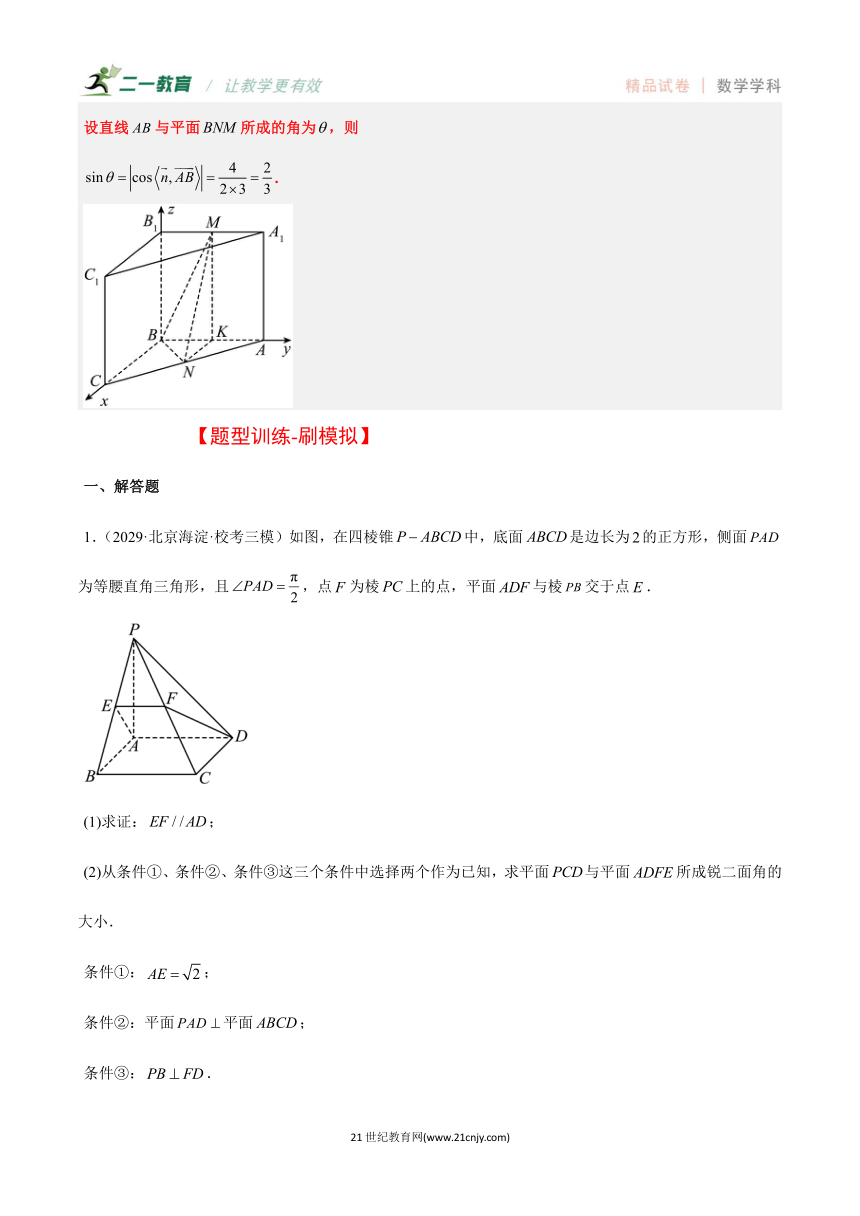
【典例1】(2022·北京·统考高考真题)如图,在三棱柱中,侧面为正方形,平面平面,,M,N分别为,AC的中点.
(1)求证:平面;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB与平面BMN所成角的正弦值.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】(1)见解析
(2)见解析
【分析】(1)取的中点为,连接,可证平面平面,从而可证平面.
(2)选①②均可证明平面,从而可建立如图所示的空间直角坐标系,利用空间向量可求线面角的正弦值.
【详解】(1)取的中点为,连接,
由三棱柱可得四边形为平行四边形,
而,则,
而平面,平面,故平面,
而,则,同理可得平面,
而平面,
故平面平面,而平面,故平面,
(2)因为侧面为正方形,故,
而平面,平面平面,
平面平面,故平面,
因为,故平面,
因为平面,故,
若选①,则,而,,
故平面,而平面,故,
所以,而,,故平面,
故可建立如所示的空间直角坐标系,则,
故,
设平面的法向量为,
则,从而,取,则,
设直线与平面所成的角为,则
.
若选②,因为,故平面,而平面,
故,而,故,
而,,故,
所以,故,
而,,故平面,
故可建立如所示的空间直角坐标系,则,
故,
设平面的法向量为,
则,从而,取,则,
设直线与平面所成的角为,则
.
【题型训练-刷模拟】
一、解答题
1.(2029·北京海淀·校考三模)如图,在四棱锥中,底面是边长为的正方形,侧面为等腰直角三角形,且,点为棱上的点,平面与棱交于点.
(1)求证:;
(2)从条件①、条件②、条件③这三个条件中选择两个作为已知,求平面与平面所成锐二面角的大小.
条件①:;
条件②:平面平面;
条件③:.
2.(2029·全国·高三专题练习)如图,在长方体中,,E为的中点.
(1)证明:平面平面;
(2)若点F在内,且,从下面三个结论中选一个求解.
①求直线 与平面所成角的正弦值;
②求平面与平面所成角的余弦值;
③求二面角的余弦值.
注:若选择多个结论分别解答,按第一个解答计分.
9.(2029·北京·统考模拟预测)如图,在三棱柱中,平面,,为线段上一点,平面交棱于点.
(1)求证:;
(2)若直线与平面所成角为,再从条件①和条件②这两个条件中选择一个作为已知,求点到平面的距离.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
4.(2029·北京海淀·校考三模)在四棱锥中,底面是边长为2的菱形,,且平面,分别是的中点,是上一点,且.
(1)求证:平面;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线与平面所成角的正弦值.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答记分.
5.(2029·全国·高三专题练习)如图在几何体中,底面为菱形,.
(1)判断是否平行于平面,并证明;
(2)再从条件①、条件②、条件③这三个条件中选择一个作为已知,求:
(i)平面与平面所成角的大小;
(ii)求点到平面的距离.
条件①:面面
条件②:
条件③:
注:如果选择多个条件分别作答,按第一个解答计分.
6.(2029·北京·校考模拟预测)如图,在四棱锥中,,,底面,为棱上的点,,.
(1)若平面,求证:点为的中点;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求平面与平面夹角的余弦值.
条件①:平面
条件②:直线与夹角的余弦值为
注:如果选择条件①和条件②分别解答,按第一个解答计分.
7.(2029·全国·高三专题练习)如图,四边形是边长为2的菱形,,四边形为矩形,,从下列三个条件中任选一个作为已知条件,并解答问题(如果选择多个条件分别解答,按第一个解答计分).
①与平面所成角相等;②三棱锥体积为;③
(1)平面平面;
(2)求二面角的大小;
(9)求点到平面的距离.
8.(2029·全国·高三专题练习)如图在三棱柱中,为的中点,,.
(1)证明:;
(2)若,且满足:______,______(待选条件).
从下面给出的①②③中选择两个填入待选条件,求二面角的正弦值.
①三棱柱的体积为;
②直线与平面所成的角的正弦值为;
③二面角的大小为60°;
注:若选择不同的组合分别解答,则按第一个解答计分.
9.(2029·甘肃兰州·统考模拟预测)如图所示的五边形中是矩形,,,沿折叠成四棱锥,点是的中点,.
(1)在四棱锥中,可以满足条件①;②;③,请从中任选两个作为补充条件,证明:侧面底面;(注:若选择不同的组合分别解答,则按第一个解答计分.)
(2)在(1)的条件下求直线与平面所成角的正弦值.
10.(2029·全国·高三专题练习)在中,,过点作,交线段于点(如图1),沿将折起,使(如图2),点分别为棱的中点.
(1)求证:;
(2)在①图1中,②图1中,③图2中三棱锥的体积最大.
这三个条件中任选一个,补充在下面问题中,再解答问题.
问题:已知__________,试在棱上确定一点,使得,并求平面与平面的夹角的余弦值.
注:如果选择多个条件分别解答,按第一个解答计分.
11.(2029·甘肃兰州·统考模拟预测)如图所示的五边形中是矩形,,,沿折叠成四棱锥,点是的中点,.
(1)在四棱锥中,可以满足条件①;②;③,请从中任选两个作为补充条件,证明:侧面底面;(注:若选择不同的组合分别解答,则按第一个解答计分.)
(2)在(1)的条件下求点到平面的距离.
12.(2029·全国·高三专题练习)如图,在四棱锥中,侧棱平面,底面四边形是矩形,,点、分别为棱、的中点,点在棱上.
(1)若,求证:直线平面;
(2)若,从下面①②两个条件中选取一个作为已知,证明另外一个成立.
①平面与平面的交线为直线,与直线成角的余弦值为;
②二面角的余弦值为.
注:若选择不同的组合分别作答,则按第一个解答计分.
19.(2029·江苏盐城·盐城中学校考模拟预测)如图,在四棱锥中,底面ABCD是矩形,底面ABCD,且,E是PC的中点,平面ABE与线段PD交于点F.
(1)证明:F为PD的中点;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线BE与平面PAD所成角的正弦值.
条件①:三角形BCF的面积为;
条件②:三棱锥的体积为1.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
14.(2029·北京·高三专题练习)如图,已知直三棱柱中,,为中点,,再从条件①,条件②这两个条件中选择一个作为已知,完成以下问题:
(1)证明:;
(2)求直线与平面所成角的正弦值.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
15.(2029·黑龙江哈尔滨·哈九中校考模拟预测)如图,已知四棱锥,底面是平行四边形,且,是线段的中点,.
(1)求证:平面;
(2)下列条件任选其一,求二面角的余弦值.
①与平面所成的角为;
②到平面的距离为.
注:如果选择多个条件分别解答,按一个解答计分.
16.(2029·江苏·统考三模)如图,三棱锥P-ABC的底面为等腰直角三角形,∠ABC=90°,AB=2.D,E分别为AC,BC的中点,PD⊥平面ABC,点M在线段PE上.
(1)再从条件①、②、③、④四个条件中选择两个作为已知,使得平面MBD⊥平面PBC,并给予证明;
(2)在(1)的条件下,求直线BP与平面MBD所成的角的正弦值.
条件①:;
条件②:∠PED=60°;
条件③:PM=9ME:
条件④:PE=9ME.
2024年高考数学高频考点题型归纳与方法总结(新高考通用)
素养拓展29 立体几何中的结构不良问题(精讲+精练)
一、空间向量与立体几何的求解公式
(1)异面直线成角:设a,b分别是两异面直线l1,l2的方向向量,则l1与l2所成的角θ满足:cos θ=;
(2)线面成角:设直线l的方向向量为a,平面α的法向量为n,a与n的夹角为β,
则直线l与平面α所成的角为θ满足:sin θ=|cos β|=.
(9)二面角:设n1,n2分别是二面角α-l-β的两个半平面α,β的法向量,
则两面的成角θ满足:cos θ=cos〈n1,n2〉=;
注意:二面角的平面角大小是向量n1与n2的夹角或是向量n1与n2的夹角的补角,具体情况要判断确定.
(4)点到平面的距离:如右图所示,已知AB为平面α的一条斜线段,n为平面α的法向量,
则点B到平面α的距离为:||=,即向量在法向量n的方向上的投影长.
二、几种常见角的取值范围
①异面直线成角∈(0,] ;②二面角∈[0,π] ;③线面角∈[0,] ;④向量夹角∈[0,π]
三、平行构造的常用方法
①三角形中位线法;②平行四边形线法;③比例线段法.
四、垂直构造的常用方法
①等腰三角形三线合一法;②勾股定理法;③投影法.
五、用向量证明空间中的平行关系
(1)线线平行:设直线l1和l2的方向向量分别为v1和v2,则l1∥l2(或l1与l2重合) v1∥v2.
(2)线面平行:设直线l的方向向量为v,平面α的法向量为u,则l∥α或l α v⊥u.
(9)面面平行:设平面α和β的法向量分别为u1,u2,则α∥β u1 ∥u2.
六、用向量证明空间中的垂直关系
(1)线线垂直:设直线l1和l2的方向向量分别为v1和v2,则l1⊥l2 v1⊥v2 v1·v2=0.
(2)线面垂直:设直线l的方向向量为v,平面α的法向量为u,则l⊥α v∥u.
(9)面面垂直:设平面α和β的法向量分别为u1和u2,则α⊥β u1⊥u2 u1·u2=0.
七、点面距常用方法
①作点到面的垂线,点到垂足的距离即为点到平面的距离;②等体积法;③向量法
【典例1】(2022·北京·统考高考真题)如图,在三棱柱中,侧面为正方形,平面平面,,M,N分别为,AC的中点.
(1)求证:平面;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB与平面BMN所成角的正弦值.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】(1)见解析
(2)见解析
【分析】(1)取的中点为,连接,可证平面平面,从而可证平面.
(2)选①②均可证明平面,从而可建立如图所示的空间直角坐标系,利用空间向量可求线面角的正弦值.
【详解】(1)取的中点为,连接,
由三棱柱可得四边形为平行四边形,
而,则,
而平面,平面,故平面,
而,则,同理可得平面,
而平面,
故平面平面,而平面,故平面,
(2)因为侧面为正方形,故,
而平面,平面平面,
平面平面,故平面,
因为,故平面,
因为平面,故,
若选①,则,而,,
故平面,而平面,故,
所以,而,,故平面,
故可建立如所示的空间直角坐标系,则,
故,
设平面的法向量为,
则,从而,取,则,
设直线与平面所成的角为,则
.
若选②,因为,故平面,而平面,
故,而,故,
而,,故,
所以,故,
而,,故平面,
故可建立如所示的空间直角坐标系,则,
故,
设平面的法向量为,
则,从而,取,则,
设直线与平面所成的角为,则
.
【题型训练-刷模拟】
一、解答题
1.(2029·北京海淀·校考三模)如图,在四棱锥中,底面是边长为的正方形,侧面为等腰直角三角形,且,点为棱上的点,平面与棱交于点.
(1)求证:;
(2)从条件①、条件②、条件③这三个条件中选择两个作为已知,求平面与平面所成锐二面角的大小.
条件①:;
条件②:平面平面;
条件③:.
【答案】(1)证明见解析
(2)
【分析】(1)由底面是正方形得,用线面平行的判定定理证得平面,再用线面平行的性质定理证得;
(2) 若选条件①②,由平面平面得,,由为正方形得,即可建立空间直角坐标系,由点的坐标求出向量的坐标,从而求出平面和平面的法向量,代入夹角公式即可求出平面与平面所成锐二面角的大小;若选条件①③,易证得平面,从而证得,所以平面,从而得到,又因为,则可说明为等腰直角三角形,即可建立与①②相同的空间直角坐标系,下面用与①②相同的过程求解;若选条件②③,由平面平面,可证平面,所以,,又由平面,可证,结合可得点为的中点,则可得,即可建立与①②相同的空间直角坐标系,下面用与①②相同的过程求解.
【详解】(1)证明:因为底面是正方形,所以,
平面,平面,所以平面,
又因为平面与交于点,平面,平面平面
所以.
(2)选条件①②,则,平面平面.
因为侧面为等腰直角三角形,且,即,,
因为平面平面,平面平面,平面,
所以平面,
又因为平面,平面,所以,,
又由为正方形得.
以点为坐标原点,,,分别为轴,轴,轴正方向,建立如图所示空间直角坐标系,
则,,,,,
因为,所以点为的中点,则,
从而,,, ,
设平面的法向量为,则,
令,可得,
设平面的法向量为,则,
令,可得,
所以,
则两平面所成的锐二面角为.
选条件①③,则,.
侧面为等腰直角三角形,且,即,,
因为,,且两直线在平面内,可得平面,
因为平面,则.
又因为,,且两直线在平面内,
则平面,
因为平面则,
因为,所以为等腰三角形,所以点为的中点.
又因为,所以为等腰直角三角形,
则可建立与①②相同的空间直角坐标系,以下用与①②相同的过程求解.
选条件②③,则平面平面,.
因为侧面为等腰直角三角形,且,
即,,
因为平面平面,平面平面,平面,
所以平面,
又因为平面,平面,所以,,
又由为正方形得.
因为,,且两直线在平面内,则平面,
因为平面,则,
因为,所以为等腰三角形,所以点为的中点,则.
则可建立与①②相同的空间直角坐标系,以下的过程与①②相同.
2.(2029·全国·高三专题练习)如图,在长方体中,,E为的中点.
(1)证明:平面平面;
(2)若点F在内,且,从下面三个结论中选一个求解.
①求直线 与平面所成角的正弦值;
②求平面与平面所成角的余弦值;
③求二面角的余弦值.
注:若选择多个结论分别解答,按第一个解答计分.
【答案】(1)证明见解析
(2)答案见解析
【分析】(1)故以为坐标原点,,,所在直线分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系,分别求出平面平面的法向量,由,即可证明;
(2)选①,分别求出直线的方向向量与平面的法向量,由线面角的向量公式求解即可;选②、③,分别求出两个平面的法向量,由二面角的向量公式代入即可得出答案.
【详解】(1)因为是长方体,所以,,两两垂直,
故以为坐标原点,,,所在直线分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系.
因为,所以,,,,.
则,,,.
设平面EAB的法向量为,则即
令,则,,得;
设平面的法向量为,则即
令,则,,得.
因为,所以,故平面平面.
(2)取的中点H,由长方体的性质易得,,连接,
所以四边形为平行四边形,,
因为,所以平面,
所以平面,即平面.
由是等边三角形,易得三棱锥为正三棱锥,
所以点F为等边的中心,故,.
选择结论①:
由(1)得平面的一个法向量为.
设直线BF与平面所成角为,则,
所以BF与平面所成角的正弦值为.
选择结论②:
由(1)得平面EAB的一个法向量,又,,
设平面FAB的法向量为,则即
令a=0,得b=5,c=2,则.
设平面FAB与平面EAB所成角为,则.
选择结论③:
因为点F在内,,所以为直线与平面的交点,
所以平面的一个法向量为.
又,,
设平面FAB的法向量为,则即令a=0,得b=5,c=2,则.
设二面角为,则.
观察图形可得二面角为钝二面角,所以二面角的余弦值为.
9.(2029·北京·统考模拟预测)如图,在三棱柱中,平面,,为线段上一点,平面交棱于点.
(1)求证:;
(2)若直线与平面所成角为,再从条件①和条件②这两个条件中选择一个作为已知,求点到平面的距离.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】(1)证明见解析
(2).
【分析】(1)由线面平行的性质定理证明即可;
(2)建立空间直角坐标系,利用坐标法计算点到平面的距离即可.
【详解】(1)证明:由题意可知,
因为三棱柱,平面
所以侧面为矩形
面,平面
平面
又平面平面
且平面
(2)解:若选择条件①,
平面,平面,平面,
,,
又
两两垂直;
若选择条件②,
平面,平面,平面,
,,
又,,
,
两两垂直;
以下条件①和条件②的计算过程相同,
因为两两垂直,所以如图建立空间直角坐直角坐标系.
可得,.
则,.
设,
则
.
设为平面的法向量,
则即
令,则,,可得.
则.
解得,则.
因为,
所以点到平面的距离为.
4.(2029·北京海淀·校考三模)在四棱锥中,底面是边长为2的菱形,,且平面,分别是的中点,是上一点,且.
(1)求证:平面;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线与平面所成角的正弦值.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答记分.
【答案】(1)证明见解析;
(2).
【分析】(1)通过证明即可证明结论;
(2)以O为原点建立空间直角坐标系,由选择条件可得相应点坐标,可得向量PA坐标与平面法向量坐标,即可得答案.
【详解】(1)因G,F分别为中点,则为中位线,则.
又平面,平面,则平面.
(2)如图以O为原点建立空间直角坐标系.
若选①,因,底面是边长为2的菱形,则,
若选②,因,底面是边长为2的菱形,则,
则,.
所以.
又,则,得.
则,.
设平面法向量为,则.
得,又,设直线与平面所成角为.
则.
5.(2029·全国·高三专题练习)如图在几何体中,底面为菱形,.
(1)判断是否平行于平面,并证明;
(2)再从条件①、条件②、条件③这三个条件中选择一个作为已知,求:
(i)平面与平面所成角的大小;
(ii)求点到平面的距离.
条件①:面面
条件②:
条件③:
注:如果选择多个条件分别作答,按第一个解答计分.
【答案】(1)与平面不平行,证明见解析
(2)(i);(ii)
【分析】(1)利用线面平行的判定定理构造平行四边形得线线平行,即可得结论;
(2)选择条件证明线线垂直建立空间直角坐标系,利用空间向量的坐标运算求解平面与平面的角及点到平面距离.
【详解】(1)不平行于平面,理由如下:
取中点,
因为,所以
则四边形为平行四边形,所以,又,所以不平行于,
假设平面,因为平面平面,平面
所以,与不平行于矛盾,所以假设不成立,即不平行于平面;
(2)选择条件①:
取中点,连接
因为菱形,所以为正三角形,又为中点,所以,
由于,所以,
又因为面面,面面,面
所以面,因为面,所以
又因为,面,所以面,
而面,所以,
所以如图,以为原点,所在直线为轴建立空间直角坐标系,
则
(i)因为面,所以为平面的一个法向量
设平面的法向量为,因为
所以,令,
设平面与平面所成角为,
所以,则
即平面与平面所成角大小为;
(ii)因为,由(i)知平面的一个法向量为
所以点到平面的距离为.
选择条件②:连接,取中点,连接
因为菱形,所以为正三角形,又为中点,所以,由于,所以,
在菱形中,有,
又因为,平面,所以平面,
因为平面,所以
又因为,面,所以面,
而面,所以,
所以如图,以为原点,所在直线为轴建立空间直角坐标系,
则
(i)因为面,所以为平面的一个法向量
设平面的法向量为,因为
所以,令,
设平面与平面所成角为,
所以,则
即平面与平面所成角大小为;
(ii)因为,由(i)知平面的一个法向量为
所以点到平面的距离为.
条件③:
取中点,连接
因为菱形,所以为正三角形,又为中点,所以,由于,所以,
因为,由(1)可得,所以
所以,即
因为,所以
又因为,面,所以面,
而面,所以,
所以如图,以为原点,所在直线为轴建立空间直角坐标系,
则
(i)因为面,所以为平面的一个法向量
设平面的法向量为,因为
所以,令,
设平面与平面所成角为,
所以,则
即平面与平面所成角大小为;
(ii)因为,由(i)知平面的一个法向量为
所以点到平面的距离为.
6.(2029·北京·校考模拟预测)如图,在四棱锥中,,,底面,为棱上的点,,.
(1)若平面,求证:点为的中点;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求平面与平面夹角的余弦值.
条件①:平面
条件②:直线与夹角的余弦值为
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】(1)证明见解析
(2)
【分析】(1)利用线面平行的性质证明线线平行,即可得结论;
(2)以为坐标原点,建立空间直角坐标系,选择条件①,利用平面,确定的坐标,进而利用向量法可求平面与平面夹角的余弦值;选择条件②,利用直线与夹角的余弦值为,确定的坐标,进而利用向量法可求平面与平面夹角的余弦值.
【详解】(1)证明:过作交于,连接,如图所示:
,,,确定平面,
平面,平面,
平面平面,
,
∴四边形为平行四边形,则
为的中位线,点为的中点;
(2)选择条件①:平面
底面,,
以为坐标原点,建立如图所示的空间直角坐标系,
则,0,,,0,,,2,,,0,,,1,,
设,,,且,,,,,
,2,,,,,2,,
,,,
,,,
,,,,1,,
设平面的一个法向量为,,,
则,令,则,,
平面的一个法向量为,,,
,0,,若平面,则,
,解得,,,,
平面,,0,是平面的一个法向量,
则,,
平面与平面夹角的余弦值为.
选择条件②:直线与夹角的余弦值为
底面,,
以为坐标原点,建立如图所示的空间直角坐标系,
则,0,,,0,,,2,,,0,,,1,,
设,,,且,,,,,
,2,,,,,2,,
,,,
,,,
,,,,1,,
直线与夹角的余弦值为
,整理得,解得或(舍),
设平面的一个法向量为,,,
则,令,则,,
平面的一个法向量为,,,
平面,,0,是平面的一个法向量,
则,,
平面与平面夹角的余弦值为.
7.(2029·全国·高三专题练习)如图,四边形是边长为2的菱形,,四边形为矩形,,从下列三个条件中任选一个作为已知条件,并解答问题(如果选择多个条件分别解答,按第一个解答计分).
①与平面所成角相等;②三棱锥体积为;③
(1)平面平面;
(2)求二面角的大小;
(9)求点到平面的距离.
【答案】(1)证明见解析
(2)
(9)
【分析】(1)若选①,则作面,证明和重合从而得到面,从而得到面面垂直;若选②,计算得到到面的距离,得到面,从而得到面面垂直;若选③,通过余弦定理计算得到,再通过面,从而得到面面垂直;
(2)通过建立空间直角坐标系,求出两个平面的法向量,结合二面角计算公式计算即可;
(9)通过点面距离的计算公式直接计算即可.
【详解】(1)选①,连接,作面,垂足为.
与平面所成角相等,
,
在的中垂线上,
在平面内,,
和重合,
面,
又面,
面面
若选②,设到面的距离为,
,得,
即为到面的距离,即面,
又面,
面面.
若选③,由余弦定理得,,
,又面
面,
又面
面面
(2)因为面,面,
所以,
取中点,则,
所以,又因为,
所以建立如下图所示空间直角坐标系,
,
,
设平面的一个法向量为,
则,即,
令,则,
设平面的一个法向量为,
则,即,
令,则,
,
,
由图可知二面角是钝角,
所以二面角的大小为.
(9),
平面的一个法向量为,
点到平面的距离.
8.(2029·全国·高三专题练习)如图在三棱柱中,为的中点,,.
(1)证明:;
(2)若,且满足:______,______(待选条件).
从下面给出的①②③中选择两个填入待选条件,求二面角的正弦值.
①三棱柱的体积为;
②直线与平面所成的角的正弦值为;
③二面角的大小为60°;
注:若选择不同的组合分别解答,则按第一个解答计分.
【答案】(1)证明见解析
(2)答案见解析
【分析】(1)通过证明平面来证得.
(2)先选择条件,然后根据所选条件,利用几何法或向量法求得二面角的正弦值.
【详解】(1)在三棱柱中,由题意可得,,,
∴,又∵,∴,
同时在中,∵,,∴,
∵平面,
∴平面,
又∵平面,∴.
(2)∵,且,∴平面,
方案一:选择①③
∵平面,∴,,
∴为二面角的平面角,即,
∴,又∵三棱柱的体积为,∴.
法一:取的中点为,连接,,过作于点,连接,
∵平面,∴平面,
又∵,由三垂线定理可得,
∴为二面角的平面角,
其中,,,则,
由于二面角的平面角与二面角的平面角互补,
故二面角的正弦值为.
法二:过作,过作,过作交于点,连接,
∴为二面角的平面角,其中,,,
∴,故二面角的正弦值为.
法三:如图所示,建立空间直角坐标系,
设平面的一个法向量为,且,,
则,令,则,,故,
设平面的一个法向量为,且,,
则,
令,则,,故,
,故二面角的正弦值为.
方案二:选择①②;
解析:过点作于点∵平面平面,,
∴平面,故直线与平面所成角为,且,
设,,则,即,.
余下解法参考方案一.
方案三:选择②③;
∵平面,∴,,
∴为二面角的平面角,即,
过点作于点,
∵平面平面且交线为,,平面,
∴平面,故直线与平面所成角为,且.
设,则,即.
余下解法参考方案一.
9.(2029·甘肃兰州·统考模拟预测)如图所示的五边形中是矩形,,,沿折叠成四棱锥,点是的中点,.
(1)在四棱锥中,可以满足条件①;②;③,请从中任选两个作为补充条件,证明:侧面底面;(注:若选择不同的组合分别解答,则按第一个解答计分.)
(2)在(1)的条件下求直线与平面所成角的正弦值.
【答案】(1)证明见解析
(2)
【分析】(1)选条件①②,利用勾股定理得到,进而得到底面,利用面面垂直的判定定理即可得证;
选条件①③,利用正弦定理得到,进而得到底面,利用面面垂直的判定定理即可得证;
选条件②③,利用余弦定理和勾股定理得到,进而得到底面,利用面面垂直的判定定理即可得证;
(2)由(1)可得平面,建立空间直角坐标系,利用空间向量法计算可得.
【详解】(1)证明:(1)方案一:选条件①②.
因为在四棱锥中,点是的中点,,所以,
又因为在中,,所以,
又因为是矩形,,所以,,
由可得,所以,
则由,,,平面,所以平面,又因为侧面,
所以侧面底面;
方案二:选条件①③.
因为在四棱锥中,点是的中点,,所以,
又因为在中,,
所以由正弦定理得:,即,所以,
即,所以,
则由,,,平面,所以平面,又因为侧面,
所以侧面底面;
方案三:选条件②③.
因为在四棱锥中,点是的中点,,所以,
又因为在中,,所以,
又因为是矩形,,所以,
又因为在中,,则,
设,,
所以有,解得或(舍,所以,
由可得,所以,
则由,,,平面,所以平面,又因为侧面,
所以侧面底面;
(2)在(1)条件下知平面,且,
故如图所示:以为坐标原点,以所在直线为轴,以所在直线为轴,以所在直线为轴,建立空间直角坐标系,
则,,,,
则,,
设平面的法向量为,则,则,
,
设直线与平面所成角为,则,
直线与平面所成角的正弦值为.
10.(2029·全国·高三专题练习)在中,,过点作,交线段于点(如图1),沿将折起,使(如图2),点分别为棱的中点.
(1)求证:;
(2)在①图1中,②图1中,③图2中三棱锥的体积最大.
这三个条件中任选一个,补充在下面问题中,再解答问题.
问题:已知__________,试在棱上确定一点,使得,并求平面与平面的夹角的余弦值.
注:如果选择多个条件分别解答,按第一个解答计分.
【答案】(1)证明见解析
(2).
【分析】(1)根据线面垂直的判定定理与性质可得,结合中位线的性质可得,即可证明;
(2)选①:由二倍角的正切公式求出,进而求出BD,选②:根据向量的线性运算求出BD,选③:设,利用线面垂直的判定定理和性质可得平面,则,利用导数求出体积的最大值,求出BD.分别建立如图空间直角坐标系,利用向量法求出面面角即可;
【详解】(1),平面,
平面平面.
又分别为的中点,
.
(2)选①,在图1所示的中,由,
解得或(舍去).
设,在Rt中,,
解得.
以点为原点,分别为轴建立如图所示的坐标系,
,
则.
设,则.
,即,解得,
当(即是的靠近的一个四等分点)时,.
设平面的一个法向量为,且,
由得令,则,
取平面CBN的一个法向量,
则,
平面BMN与平面的夹角的余弦值为.
选②,在图1所示的中,设,
则,
又,由平面向量基本定理知,即.
以点为原点,分别为轴建立如图所示的空间直角坐标系,
,
则.
设,则,
即,解得,
当(即是的靠近的一个四等分点)时,.
设平面的一个法向量为,且,
由得令,则.
取平面的一个法向量,
则,
平面与平面的夹角的余弦值为.
选③,在图1所示的中,设,则,
为等腰直角三角形,.
折起后,且,平面,
平面,又,
,
令,
当时,;当时,,
时,三棱锥的体积最大.
以点为原点,分别为轴建立如图所示直角坐标系,
,
,则,
设,则.
,即,
解得,
当(即是的靠近的一个四等分点)时,.
设平面的一个法向量为,且,
由得令,则.
取平面的一个法向量,
则,
平面与平面的夹角的余弦值为.
11.(2029·甘肃兰州·统考模拟预测)如图所示的五边形中是矩形,,,沿折叠成四棱锥,点是的中点,.
(1)在四棱锥中,可以满足条件①;②;③,请从中任选两个作为补充条件,证明:侧面底面;(注:若选择不同的组合分别解答,则按第一个解答计分.)
(2)在(1)的条件下求点到平面的距离.
【答案】(1)条件选择见解析,证明见解析
(2)
【分析】(1)选条件①②,利用勾股定理逆定理证得,由等腰三角形的几何性质可得出,利用线面和面面垂直的判定定理可证得结论成立;
选条件 ①③,利用正弦定理推导出,,由等腰三角形的几何性质可得出,利用线面和面面垂直的判定定理可证得结论成立;
选条件②③,利用余弦定理求出的长,利用勾股定理逆定理证得,由等腰三角形的几何性质可得出,利用线面和面面垂直的判定定理可证得结论成立;
(2)计算出三棱锥的体积,计算出的面积,利用等体积法可求得点到平面的距离.
【详解】(1)证明:方案一:选条件①②.
因为在四棱锥中,,点为的中点,则,
因为,在中,,,
又因为四边形为矩形,,则,,
因为,,,所以,,则,
因为,、平面,所以,平面,
因为平面,所以,侧面平面;
方案二:选条件①③.
因为在四棱锥中,,点为的中点,则,
在中,,,,
由正弦定理可得,即,所以,,
所以,,即,
因为,、平面,所以,平面,
因为平面,所以,侧面平面;
方案三:选条件②③.
因为在四棱锥中,,点为的中点,则,且,
在中,,,
又因为四边形为矩形,,则,
所以,,
在中,,则,
设,由余弦定理可得,
整理可得,解得或(舍),所以,,
因为,,,所以,,则,
因为,、平面,所以,平面,
因为平面,所以,侧面平面.
(2)解:在(1)的条件下,平面,
因为为的中点,,,
在中,,,则,
所以,,则,
,
在中,,,则,
所以,,
所以,,
设点到平面的距离为,由可得,
所以,.
因此,点到平面的距离为.
12.(2029·全国·高三专题练习)如图,在四棱锥中,侧棱平面,底面四边形是矩形,,点、分别为棱、的中点,点在棱上.
(1)若,求证:直线平面;
(2)若,从下面①②两个条件中选取一个作为已知,证明另外一个成立.
①平面与平面的交线为直线,与直线成角的余弦值为;
②二面角的余弦值为.
注:若选择不同的组合分别作答,则按第一个解答计分.
【答案】(1)证明见解析
(2)条件选择见解析,证明见解析
【分析】(1)取的中点,连接、,证明出平面平面,利用面面平行的性质可证得结论成立;
(2)若选①,分析可知异面直线与所成的角即为,由结合勾股定理可求得的长,然后以点为坐标原点,、、的方向分别为、、轴的正方向建立空间直角坐标系,利用空间向量法可求得二面角的余弦值;
若选②,以点为坐标原点,、、的方向分别为、、轴的正方向建立空间直角坐标系,设,利用空间向量法可求得的值,分析可知异面直线与所成的角即为,求出的余弦值即可.
【详解】(1)证明:如下图所示,取的中点,连接、,
因为、分别为、的中点,所以,,
因为平面,平面,所以,平面,
又因为,所以,,
因为平面,平面,所以,平面,
因为,、平面,故平面平面,
因为平面,所以,平面.
(2)证明:若选①作为已知条件,平面与平面的交线为直线,作出直线如图,
由于,平面,平面,所以,平面,
因为平面,平面平面,所以,,
所以,异面直线与所成的角即为,
因为,则,则,
故,
以点为坐标原点,、、的方向分别为、、轴的正方向建立如下图所示的空间直角坐标系,
则、、、,,,
设平面的法向量为,则,
取,可得,易知平面的一个法向量为,
则,
由图可知,二面角为锐角,故二面角的余弦值为;
若选②为已知条件,以点为坐标原点,、、的方向分别为、、轴的正方向建立如图所示的空间直角坐标系,
设,则、、,,。
设平面的的法向量为,则,
取,可得,
易知平面的一个法向量为,且二面角的余弦值为,
则,解得,
平面与平面的交线为直线,作出直线如图,
由于,平面,平面,所以,平面,
因为平面,平面平面,所以,,
所以,异面直线与所成的角即为,
因为,则,
则.
19.(2029·江苏盐城·盐城中学校考模拟预测)如图,在四棱锥中,底面ABCD是矩形,底面ABCD,且,E是PC的中点,平面ABE与线段PD交于点F.
(1)证明:F为PD的中点;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线BE与平面PAD所成角的正弦值.
条件①:三角形BCF的面积为;
条件②:三棱锥的体积为1.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】(1)证明见解析
(2)
【分析】(1)由线面平行的判定证面,再由线面平行的性质可证,进而有△中为中位线,即可证结论;
(2)由线面垂直的性质、判定证两两垂直,且面,构建空间直角坐标系,根据所选条件求得,进而求直线方向向量和面的法向量,利用线面角夹角的向量求法求其正弦值.
【详解】(1)由底面ABCD是矩形,则,而面,面,
所以面,
又E是PC的中点,面ABE与线段PD交于点F,即面面,
而面,则,故,
△中为中位线,故F为PD的中点;
(2)由底面ABCD,面,则,又,
由,面,则面,
由面,故,即△为直角三角形,且;
由面,则面面,同理有面面;
又面,故,又,
所以两两垂直,可构建如下空间直角坐标系,
选①,则,故,而,
选②,由,而,所以;
此时,,,则,
又是面的一个法向量,若直线BE与平面PAD所成角为,
所以.
14.(2029·北京·高三专题练习)如图,已知直三棱柱中,,为中点,,再从条件①,条件②这两个条件中选择一个作为已知,完成以下问题:
(1)证明:;
(2)求直线与平面所成角的正弦值.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】(1)证明详见解析
(2)条件选择见解析,直线与平面所成角的正弦值为
【分析】(1)若选①,则通过证明平面来证得.若选②,则先证明,然后通过证明平面来证得.
(2)建立空间直角坐标系,利用向量法求得直线与平面所成角的正弦值.
【详解】(1)若选择条件①:,连接,
在直三棱柱中,平面,平面,
所以.
在三角形中,,为的中点,
所以,由于,平面,
所以平面,由于平面,所以,
由于,,平面,
所以平面,
由于平面,所以.
若选择条件②:,连接,
由于是中点,所以,
根据直三棱柱的性质可知,
由于平面,所以平面,
由于平面,所以.
由于,所以,
所以,则,则,
由于,平面,所以平面,
由于平面,所以.
(2)先得到:
若选①,则在中,由,得,
又,所以,.
若选②,则.
在三角形中,,所以,
所以,
根据直三棱柱的性质可知,,
以点为原点,分别以为轴建立空间直角坐标系,
则,,,,,,
,,,
设平面的法向量为,则,
令,得,
设直线与平面所成角为,
则.
15.(2029·黑龙江哈尔滨·哈九中校考模拟预测)如图,已知四棱锥,底面是平行四边形,且,是线段的中点,.
(1)求证:平面;
(2)下列条件任选其一,求二面角的余弦值.
①与平面所成的角为;
②到平面的距离为.
注:如果选择多个条件分别解答,按一个解答计分.
【答案】(1)证明见解析
(2)
【分析】(1)根据平行四边形中的几何关系可得再根据勾股定理可得,利用线面垂直的判定定理即可证明结果;
(2)选①,取中点为,连接,根据几何关系可得,根据(1)可得,根据线面垂直的判定定理可得平面,则与平面所成的角为,由此计算出,进而计算得,可得为等边三角形;
选②,取中点为,连接,计算长度及根据等体积法可求得,即可得为等边三角形,建立合适的空间直角坐标系,求得各个点的坐标,进而求得平面的法向量及平面的法向量,根据法向量夹角的余弦值的绝对值即为二面角的余弦值绝对值即可求得结果.
【详解】(1)证明:因为,且,故,
在中,,
由余弦定理可得:,
解得,在中,,
所以,即,
又因为平面,平面,
所以平面;
(2)选①,取中点为,连接,如图所示:
因为,故,由(1)得平面,
因为平面,所以,
因为,平面,平面,
所以平面,所以为与平面所成的角,
即,因为,,
所以为等边三角形,且边长为1,所以,,
由可得,
因为,,
所以,所以为等边三角形,
以为原点,为在轴正方向建立如图所示空间直角坐标系:
所以,
,
设是平面的法向量,
则,即,
取,可得,
设为平面的法向量,
则,即,
取,可得,
设二面角所成的角为,则,
所以二面角的余弦值为.
选②, 取中点为,连接,如图所示:
因为,故,由(1)得平面,
因为平面,所以,
因为,平面,平面,所以平面,
设到平面的距离为,
因为,,所以等边三角形,
所以,,设,则,
因为,所以,
因为,为中点,所以,
所以,由,,
平面,平面,所以平面,
因为平面,所以,即,
所以,因为,
即,
即,
解得,即,所以,所以为等边三角形,
以为原点,为在轴正方向建立如图所示空间直角坐标系:
所以,
,
设是平面的法向量,
则,即,
取,可得,
设为平面的法向量,
则,即,
取,可得,
设所成的角为,则,
所以二面角的余弦值为.
16.(2029·江苏·统考三模)如图,三棱锥P-ABC的底面为等腰直角三角形,∠ABC=90°,AB=2.D,E分别为AC,BC的中点,PD⊥平面ABC,点M在线段PE上.
(1)再从条件①、②、③、④四个条件中选择两个作为已知,使得平面MBD⊥平面PBC,并给予证明;
(2)在(1)的条件下,求直线BP与平面MBD所成的角的正弦值.
条件①:;
条件②:∠PED=60°;
条件③:PM=9ME:
条件④:PE=9ME.
【答案】(1)答案见解析
(2)答案见解析
【分析】(1)如图,建立以D为原点的空间直角坐标系,设,,由平面MBD⊥平面PBC,可得两平面法向量互相垂直,即可得,据此可知可选择①④或②③;
(2)由(1)所建立空间直角坐标系及平面MBD法向量,利用向量方法可得答案.
【详解】(1)因PD⊥平面ABC,平面ABC,平面ABC,则,
又由题可知,则如图,建立以D为原点的空间直角坐标系,
则,,,,
设,.
则,,,,.
故.
设平面MBD法向量为,
则,令,可得;
设平面PBC法向量为,
则,可令,可得.
要使平面MBD⊥平面PBC,需满足.
注意到条件①,
PD⊥平面ABC,平面ABC,,又由题可知,则条件②,
条件③,条件④.
则当条件①④成立或条件②③成立时,都有,即可以使平面MBD⊥平面PBC;
(2)由(1),当选择①④时,,,.
则,平面MBD法向量为,
设BP与平面MBD所成角为,则;
当选择②③时,,,.
则,平面MBD法向量,
设BP与平面MBD所成角为,则;
.
21世纪教育网(www.21cnjy.com)
素养拓展29 立体几何中的结构不良问题(精讲+精练)
一、空间向量与立体几何的求解公式
(1)异面直线成角:设a,b分别是两异面直线l1,l2的方向向量,则l1与l2所成的角θ满足:cos θ=;
(2)线面成角:设直线l的方向向量为a,平面α的法向量为n,a与n的夹角为β,
则直线l与平面α所成的角为θ满足:sin θ=|cos β|=.
(9)二面角:设n1,n2分别是二面角α-l-β的两个半平面α,β的法向量,
则两面的成角θ满足:cos θ=cos〈n1,n2〉=;
注意:二面角的平面角大小是向量n1与n2的夹角或是向量n1与n2的夹角的补角,具体情况要判断确定.
(4)点到平面的距离:如右图所示,已知AB为平面α的一条斜线段,n为平面α的法向量,
则点B到平面α的距离为:||=,即向量在法向量n的方向上的投影长.
二、几种常见角的取值范围
①异面直线成角∈(0,] ;②二面角∈[0,π] ;③线面角∈[0,] ;④向量夹角∈[0,π]
三、平行构造的常用方法
①三角形中位线法;②平行四边形线法;③比例线段法.
四、垂直构造的常用方法
①等腰三角形三线合一法;②勾股定理法;③投影法.
五、用向量证明空间中的平行关系
(1)线线平行:设直线l1和l2的方向向量分别为v1和v2,则l1∥l2(或l1与l2重合) v1∥v2.
(2)线面平行:设直线l的方向向量为v,平面α的法向量为u,则l∥α或l α v⊥u.
(9)面面平行:设平面α和β的法向量分别为u1,u2,则α∥β u1 ∥u2.
六、用向量证明空间中的垂直关系
(1)线线垂直:设直线l1和l2的方向向量分别为v1和v2,则l1⊥l2 v1⊥v2 v1·v2=0.
(2)线面垂直:设直线l的方向向量为v,平面α的法向量为u,则l⊥α v∥u.
(9)面面垂直:设平面α和β的法向量分别为u1和u2,则α⊥β u1⊥u2 u1·u2=0.
七、点面距常用方法
①作点到面的垂线,点到垂足的距离即为点到平面的距离;②等体积法;③向量法
【典例1】(2022·北京·统考高考真题)如图,在三棱柱中,侧面为正方形,平面平面,,M,N分别为,AC的中点.
(1)求证:平面;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB与平面BMN所成角的正弦值.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】(1)见解析
(2)见解析
【分析】(1)取的中点为,连接,可证平面平面,从而可证平面.
(2)选①②均可证明平面,从而可建立如图所示的空间直角坐标系,利用空间向量可求线面角的正弦值.
【详解】(1)取的中点为,连接,
由三棱柱可得四边形为平行四边形,
而,则,
而平面,平面,故平面,
而,则,同理可得平面,
而平面,
故平面平面,而平面,故平面,
(2)因为侧面为正方形,故,
而平面,平面平面,
平面平面,故平面,
因为,故平面,
因为平面,故,
若选①,则,而,,
故平面,而平面,故,
所以,而,,故平面,
故可建立如所示的空间直角坐标系,则,
故,
设平面的法向量为,
则,从而,取,则,
设直线与平面所成的角为,则
.
若选②,因为,故平面,而平面,
故,而,故,
而,,故,
所以,故,
而,,故平面,
故可建立如所示的空间直角坐标系,则,
故,
设平面的法向量为,
则,从而,取,则,
设直线与平面所成的角为,则
.
【题型训练-刷模拟】
一、解答题
1.(2029·北京海淀·校考三模)如图,在四棱锥中,底面是边长为的正方形,侧面为等腰直角三角形,且,点为棱上的点,平面与棱交于点.
(1)求证:;
(2)从条件①、条件②、条件③这三个条件中选择两个作为已知,求平面与平面所成锐二面角的大小.
条件①:;
条件②:平面平面;
条件③:.
2.(2029·全国·高三专题练习)如图,在长方体中,,E为的中点.
(1)证明:平面平面;
(2)若点F在内,且,从下面三个结论中选一个求解.
①求直线 与平面所成角的正弦值;
②求平面与平面所成角的余弦值;
③求二面角的余弦值.
注:若选择多个结论分别解答,按第一个解答计分.
9.(2029·北京·统考模拟预测)如图,在三棱柱中,平面,,为线段上一点,平面交棱于点.
(1)求证:;
(2)若直线与平面所成角为,再从条件①和条件②这两个条件中选择一个作为已知,求点到平面的距离.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
4.(2029·北京海淀·校考三模)在四棱锥中,底面是边长为2的菱形,,且平面,分别是的中点,是上一点,且.
(1)求证:平面;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线与平面所成角的正弦值.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答记分.
5.(2029·全国·高三专题练习)如图在几何体中,底面为菱形,.
(1)判断是否平行于平面,并证明;
(2)再从条件①、条件②、条件③这三个条件中选择一个作为已知,求:
(i)平面与平面所成角的大小;
(ii)求点到平面的距离.
条件①:面面
条件②:
条件③:
注:如果选择多个条件分别作答,按第一个解答计分.
6.(2029·北京·校考模拟预测)如图,在四棱锥中,,,底面,为棱上的点,,.
(1)若平面,求证:点为的中点;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求平面与平面夹角的余弦值.
条件①:平面
条件②:直线与夹角的余弦值为
注:如果选择条件①和条件②分别解答,按第一个解答计分.
7.(2029·全国·高三专题练习)如图,四边形是边长为2的菱形,,四边形为矩形,,从下列三个条件中任选一个作为已知条件,并解答问题(如果选择多个条件分别解答,按第一个解答计分).
①与平面所成角相等;②三棱锥体积为;③
(1)平面平面;
(2)求二面角的大小;
(9)求点到平面的距离.
8.(2029·全国·高三专题练习)如图在三棱柱中,为的中点,,.
(1)证明:;
(2)若,且满足:______,______(待选条件).
从下面给出的①②③中选择两个填入待选条件,求二面角的正弦值.
①三棱柱的体积为;
②直线与平面所成的角的正弦值为;
③二面角的大小为60°;
注:若选择不同的组合分别解答,则按第一个解答计分.
9.(2029·甘肃兰州·统考模拟预测)如图所示的五边形中是矩形,,,沿折叠成四棱锥,点是的中点,.
(1)在四棱锥中,可以满足条件①;②;③,请从中任选两个作为补充条件,证明:侧面底面;(注:若选择不同的组合分别解答,则按第一个解答计分.)
(2)在(1)的条件下求直线与平面所成角的正弦值.
10.(2029·全国·高三专题练习)在中,,过点作,交线段于点(如图1),沿将折起,使(如图2),点分别为棱的中点.
(1)求证:;
(2)在①图1中,②图1中,③图2中三棱锥的体积最大.
这三个条件中任选一个,补充在下面问题中,再解答问题.
问题:已知__________,试在棱上确定一点,使得,并求平面与平面的夹角的余弦值.
注:如果选择多个条件分别解答,按第一个解答计分.
11.(2029·甘肃兰州·统考模拟预测)如图所示的五边形中是矩形,,,沿折叠成四棱锥,点是的中点,.
(1)在四棱锥中,可以满足条件①;②;③,请从中任选两个作为补充条件,证明:侧面底面;(注:若选择不同的组合分别解答,则按第一个解答计分.)
(2)在(1)的条件下求点到平面的距离.
12.(2029·全国·高三专题练习)如图,在四棱锥中,侧棱平面,底面四边形是矩形,,点、分别为棱、的中点,点在棱上.
(1)若,求证:直线平面;
(2)若,从下面①②两个条件中选取一个作为已知,证明另外一个成立.
①平面与平面的交线为直线,与直线成角的余弦值为;
②二面角的余弦值为.
注:若选择不同的组合分别作答,则按第一个解答计分.
19.(2029·江苏盐城·盐城中学校考模拟预测)如图,在四棱锥中,底面ABCD是矩形,底面ABCD,且,E是PC的中点,平面ABE与线段PD交于点F.
(1)证明:F为PD的中点;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线BE与平面PAD所成角的正弦值.
条件①:三角形BCF的面积为;
条件②:三棱锥的体积为1.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
14.(2029·北京·高三专题练习)如图,已知直三棱柱中,,为中点,,再从条件①,条件②这两个条件中选择一个作为已知,完成以下问题:
(1)证明:;
(2)求直线与平面所成角的正弦值.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
15.(2029·黑龙江哈尔滨·哈九中校考模拟预测)如图,已知四棱锥,底面是平行四边形,且,是线段的中点,.
(1)求证:平面;
(2)下列条件任选其一,求二面角的余弦值.
①与平面所成的角为;
②到平面的距离为.
注:如果选择多个条件分别解答,按一个解答计分.
16.(2029·江苏·统考三模)如图,三棱锥P-ABC的底面为等腰直角三角形,∠ABC=90°,AB=2.D,E分别为AC,BC的中点,PD⊥平面ABC,点M在线段PE上.
(1)再从条件①、②、③、④四个条件中选择两个作为已知,使得平面MBD⊥平面PBC,并给予证明;
(2)在(1)的条件下,求直线BP与平面MBD所成的角的正弦值.
条件①:;
条件②:∠PED=60°;
条件③:PM=9ME:
条件④:PE=9ME.
2024年高考数学高频考点题型归纳与方法总结(新高考通用)
素养拓展29 立体几何中的结构不良问题(精讲+精练)
一、空间向量与立体几何的求解公式
(1)异面直线成角:设a,b分别是两异面直线l1,l2的方向向量,则l1与l2所成的角θ满足:cos θ=;
(2)线面成角:设直线l的方向向量为a,平面α的法向量为n,a与n的夹角为β,
则直线l与平面α所成的角为θ满足:sin θ=|cos β|=.
(9)二面角:设n1,n2分别是二面角α-l-β的两个半平面α,β的法向量,
则两面的成角θ满足:cos θ=cos〈n1,n2〉=;
注意:二面角的平面角大小是向量n1与n2的夹角或是向量n1与n2的夹角的补角,具体情况要判断确定.
(4)点到平面的距离:如右图所示,已知AB为平面α的一条斜线段,n为平面α的法向量,
则点B到平面α的距离为:||=,即向量在法向量n的方向上的投影长.
二、几种常见角的取值范围
①异面直线成角∈(0,] ;②二面角∈[0,π] ;③线面角∈[0,] ;④向量夹角∈[0,π]
三、平行构造的常用方法
①三角形中位线法;②平行四边形线法;③比例线段法.
四、垂直构造的常用方法
①等腰三角形三线合一法;②勾股定理法;③投影法.
五、用向量证明空间中的平行关系
(1)线线平行:设直线l1和l2的方向向量分别为v1和v2,则l1∥l2(或l1与l2重合) v1∥v2.
(2)线面平行:设直线l的方向向量为v,平面α的法向量为u,则l∥α或l α v⊥u.
(9)面面平行:设平面α和β的法向量分别为u1,u2,则α∥β u1 ∥u2.
六、用向量证明空间中的垂直关系
(1)线线垂直:设直线l1和l2的方向向量分别为v1和v2,则l1⊥l2 v1⊥v2 v1·v2=0.
(2)线面垂直:设直线l的方向向量为v,平面α的法向量为u,则l⊥α v∥u.
(9)面面垂直:设平面α和β的法向量分别为u1和u2,则α⊥β u1⊥u2 u1·u2=0.
七、点面距常用方法
①作点到面的垂线,点到垂足的距离即为点到平面的距离;②等体积法;③向量法
【典例1】(2022·北京·统考高考真题)如图,在三棱柱中,侧面为正方形,平面平面,,M,N分别为,AC的中点.
(1)求证:平面;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB与平面BMN所成角的正弦值.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】(1)见解析
(2)见解析
【分析】(1)取的中点为,连接,可证平面平面,从而可证平面.
(2)选①②均可证明平面,从而可建立如图所示的空间直角坐标系,利用空间向量可求线面角的正弦值.
【详解】(1)取的中点为,连接,
由三棱柱可得四边形为平行四边形,
而,则,
而平面,平面,故平面,
而,则,同理可得平面,
而平面,
故平面平面,而平面,故平面,
(2)因为侧面为正方形,故,
而平面,平面平面,
平面平面,故平面,
因为,故平面,
因为平面,故,
若选①,则,而,,
故平面,而平面,故,
所以,而,,故平面,
故可建立如所示的空间直角坐标系,则,
故,
设平面的法向量为,
则,从而,取,则,
设直线与平面所成的角为,则
.
若选②,因为,故平面,而平面,
故,而,故,
而,,故,
所以,故,
而,,故平面,
故可建立如所示的空间直角坐标系,则,
故,
设平面的法向量为,
则,从而,取,则,
设直线与平面所成的角为,则
.
【题型训练-刷模拟】
一、解答题
1.(2029·北京海淀·校考三模)如图,在四棱锥中,底面是边长为的正方形,侧面为等腰直角三角形,且,点为棱上的点,平面与棱交于点.
(1)求证:;
(2)从条件①、条件②、条件③这三个条件中选择两个作为已知,求平面与平面所成锐二面角的大小.
条件①:;
条件②:平面平面;
条件③:.
【答案】(1)证明见解析
(2)
【分析】(1)由底面是正方形得,用线面平行的判定定理证得平面,再用线面平行的性质定理证得;
(2) 若选条件①②,由平面平面得,,由为正方形得,即可建立空间直角坐标系,由点的坐标求出向量的坐标,从而求出平面和平面的法向量,代入夹角公式即可求出平面与平面所成锐二面角的大小;若选条件①③,易证得平面,从而证得,所以平面,从而得到,又因为,则可说明为等腰直角三角形,即可建立与①②相同的空间直角坐标系,下面用与①②相同的过程求解;若选条件②③,由平面平面,可证平面,所以,,又由平面,可证,结合可得点为的中点,则可得,即可建立与①②相同的空间直角坐标系,下面用与①②相同的过程求解.
【详解】(1)证明:因为底面是正方形,所以,
平面,平面,所以平面,
又因为平面与交于点,平面,平面平面
所以.
(2)选条件①②,则,平面平面.
因为侧面为等腰直角三角形,且,即,,
因为平面平面,平面平面,平面,
所以平面,
又因为平面,平面,所以,,
又由为正方形得.
以点为坐标原点,,,分别为轴,轴,轴正方向,建立如图所示空间直角坐标系,
则,,,,,
因为,所以点为的中点,则,
从而,,, ,
设平面的法向量为,则,
令,可得,
设平面的法向量为,则,
令,可得,
所以,
则两平面所成的锐二面角为.
选条件①③,则,.
侧面为等腰直角三角形,且,即,,
因为,,且两直线在平面内,可得平面,
因为平面,则.
又因为,,且两直线在平面内,
则平面,
因为平面则,
因为,所以为等腰三角形,所以点为的中点.
又因为,所以为等腰直角三角形,
则可建立与①②相同的空间直角坐标系,以下用与①②相同的过程求解.
选条件②③,则平面平面,.
因为侧面为等腰直角三角形,且,
即,,
因为平面平面,平面平面,平面,
所以平面,
又因为平面,平面,所以,,
又由为正方形得.
因为,,且两直线在平面内,则平面,
因为平面,则,
因为,所以为等腰三角形,所以点为的中点,则.
则可建立与①②相同的空间直角坐标系,以下的过程与①②相同.
2.(2029·全国·高三专题练习)如图,在长方体中,,E为的中点.
(1)证明:平面平面;
(2)若点F在内,且,从下面三个结论中选一个求解.
①求直线 与平面所成角的正弦值;
②求平面与平面所成角的余弦值;
③求二面角的余弦值.
注:若选择多个结论分别解答,按第一个解答计分.
【答案】(1)证明见解析
(2)答案见解析
【分析】(1)故以为坐标原点,,,所在直线分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系,分别求出平面平面的法向量,由,即可证明;
(2)选①,分别求出直线的方向向量与平面的法向量,由线面角的向量公式求解即可;选②、③,分别求出两个平面的法向量,由二面角的向量公式代入即可得出答案.
【详解】(1)因为是长方体,所以,,两两垂直,
故以为坐标原点,,,所在直线分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系.
因为,所以,,,,.
则,,,.
设平面EAB的法向量为,则即
令,则,,得;
设平面的法向量为,则即
令,则,,得.
因为,所以,故平面平面.
(2)取的中点H,由长方体的性质易得,,连接,
所以四边形为平行四边形,,
因为,所以平面,
所以平面,即平面.
由是等边三角形,易得三棱锥为正三棱锥,
所以点F为等边的中心,故,.
选择结论①:
由(1)得平面的一个法向量为.
设直线BF与平面所成角为,则,
所以BF与平面所成角的正弦值为.
选择结论②:
由(1)得平面EAB的一个法向量,又,,
设平面FAB的法向量为,则即
令a=0,得b=5,c=2,则.
设平面FAB与平面EAB所成角为,则.
选择结论③:
因为点F在内,,所以为直线与平面的交点,
所以平面的一个法向量为.
又,,
设平面FAB的法向量为,则即令a=0,得b=5,c=2,则.
设二面角为,则.
观察图形可得二面角为钝二面角,所以二面角的余弦值为.
9.(2029·北京·统考模拟预测)如图,在三棱柱中,平面,,为线段上一点,平面交棱于点.
(1)求证:;
(2)若直线与平面所成角为,再从条件①和条件②这两个条件中选择一个作为已知,求点到平面的距离.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】(1)证明见解析
(2).
【分析】(1)由线面平行的性质定理证明即可;
(2)建立空间直角坐标系,利用坐标法计算点到平面的距离即可.
【详解】(1)证明:由题意可知,
因为三棱柱,平面
所以侧面为矩形
面,平面
平面
又平面平面
且平面
(2)解:若选择条件①,
平面,平面,平面,
,,
又
两两垂直;
若选择条件②,
平面,平面,平面,
,,
又,,
,
两两垂直;
以下条件①和条件②的计算过程相同,
因为两两垂直,所以如图建立空间直角坐直角坐标系.
可得,.
则,.
设,
则
.
设为平面的法向量,
则即
令,则,,可得.
则.
解得,则.
因为,
所以点到平面的距离为.
4.(2029·北京海淀·校考三模)在四棱锥中,底面是边长为2的菱形,,且平面,分别是的中点,是上一点,且.
(1)求证:平面;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线与平面所成角的正弦值.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答记分.
【答案】(1)证明见解析;
(2).
【分析】(1)通过证明即可证明结论;
(2)以O为原点建立空间直角坐标系,由选择条件可得相应点坐标,可得向量PA坐标与平面法向量坐标,即可得答案.
【详解】(1)因G,F分别为中点,则为中位线,则.
又平面,平面,则平面.
(2)如图以O为原点建立空间直角坐标系.
若选①,因,底面是边长为2的菱形,则,
若选②,因,底面是边长为2的菱形,则,
则,.
所以.
又,则,得.
则,.
设平面法向量为,则.
得,又,设直线与平面所成角为.
则.
5.(2029·全国·高三专题练习)如图在几何体中,底面为菱形,.
(1)判断是否平行于平面,并证明;
(2)再从条件①、条件②、条件③这三个条件中选择一个作为已知,求:
(i)平面与平面所成角的大小;
(ii)求点到平面的距离.
条件①:面面
条件②:
条件③:
注:如果选择多个条件分别作答,按第一个解答计分.
【答案】(1)与平面不平行,证明见解析
(2)(i);(ii)
【分析】(1)利用线面平行的判定定理构造平行四边形得线线平行,即可得结论;
(2)选择条件证明线线垂直建立空间直角坐标系,利用空间向量的坐标运算求解平面与平面的角及点到平面距离.
【详解】(1)不平行于平面,理由如下:
取中点,
因为,所以
则四边形为平行四边形,所以,又,所以不平行于,
假设平面,因为平面平面,平面
所以,与不平行于矛盾,所以假设不成立,即不平行于平面;
(2)选择条件①:
取中点,连接
因为菱形,所以为正三角形,又为中点,所以,
由于,所以,
又因为面面,面面,面
所以面,因为面,所以
又因为,面,所以面,
而面,所以,
所以如图,以为原点,所在直线为轴建立空间直角坐标系,
则
(i)因为面,所以为平面的一个法向量
设平面的法向量为,因为
所以,令,
设平面与平面所成角为,
所以,则
即平面与平面所成角大小为;
(ii)因为,由(i)知平面的一个法向量为
所以点到平面的距离为.
选择条件②:连接,取中点,连接
因为菱形,所以为正三角形,又为中点,所以,由于,所以,
在菱形中,有,
又因为,平面,所以平面,
因为平面,所以
又因为,面,所以面,
而面,所以,
所以如图,以为原点,所在直线为轴建立空间直角坐标系,
则
(i)因为面,所以为平面的一个法向量
设平面的法向量为,因为
所以,令,
设平面与平面所成角为,
所以,则
即平面与平面所成角大小为;
(ii)因为,由(i)知平面的一个法向量为
所以点到平面的距离为.
条件③:
取中点,连接
因为菱形,所以为正三角形,又为中点,所以,由于,所以,
因为,由(1)可得,所以
所以,即
因为,所以
又因为,面,所以面,
而面,所以,
所以如图,以为原点,所在直线为轴建立空间直角坐标系,
则
(i)因为面,所以为平面的一个法向量
设平面的法向量为,因为
所以,令,
设平面与平面所成角为,
所以,则
即平面与平面所成角大小为;
(ii)因为,由(i)知平面的一个法向量为
所以点到平面的距离为.
6.(2029·北京·校考模拟预测)如图,在四棱锥中,,,底面,为棱上的点,,.
(1)若平面,求证:点为的中点;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求平面与平面夹角的余弦值.
条件①:平面
条件②:直线与夹角的余弦值为
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】(1)证明见解析
(2)
【分析】(1)利用线面平行的性质证明线线平行,即可得结论;
(2)以为坐标原点,建立空间直角坐标系,选择条件①,利用平面,确定的坐标,进而利用向量法可求平面与平面夹角的余弦值;选择条件②,利用直线与夹角的余弦值为,确定的坐标,进而利用向量法可求平面与平面夹角的余弦值.
【详解】(1)证明:过作交于,连接,如图所示:
,,,确定平面,
平面,平面,
平面平面,
,
∴四边形为平行四边形,则
为的中位线,点为的中点;
(2)选择条件①:平面
底面,,
以为坐标原点,建立如图所示的空间直角坐标系,
则,0,,,0,,,2,,,0,,,1,,
设,,,且,,,,,
,2,,,,,2,,
,,,
,,,
,,,,1,,
设平面的一个法向量为,,,
则,令,则,,
平面的一个法向量为,,,
,0,,若平面,则,
,解得,,,,
平面,,0,是平面的一个法向量,
则,,
平面与平面夹角的余弦值为.
选择条件②:直线与夹角的余弦值为
底面,,
以为坐标原点,建立如图所示的空间直角坐标系,
则,0,,,0,,,2,,,0,,,1,,
设,,,且,,,,,
,2,,,,,2,,
,,,
,,,
,,,,1,,
直线与夹角的余弦值为
,整理得,解得或(舍),
设平面的一个法向量为,,,
则,令,则,,
平面的一个法向量为,,,
平面,,0,是平面的一个法向量,
则,,
平面与平面夹角的余弦值为.
7.(2029·全国·高三专题练习)如图,四边形是边长为2的菱形,,四边形为矩形,,从下列三个条件中任选一个作为已知条件,并解答问题(如果选择多个条件分别解答,按第一个解答计分).
①与平面所成角相等;②三棱锥体积为;③
(1)平面平面;
(2)求二面角的大小;
(9)求点到平面的距离.
【答案】(1)证明见解析
(2)
(9)
【分析】(1)若选①,则作面,证明和重合从而得到面,从而得到面面垂直;若选②,计算得到到面的距离,得到面,从而得到面面垂直;若选③,通过余弦定理计算得到,再通过面,从而得到面面垂直;
(2)通过建立空间直角坐标系,求出两个平面的法向量,结合二面角计算公式计算即可;
(9)通过点面距离的计算公式直接计算即可.
【详解】(1)选①,连接,作面,垂足为.
与平面所成角相等,
,
在的中垂线上,
在平面内,,
和重合,
面,
又面,
面面
若选②,设到面的距离为,
,得,
即为到面的距离,即面,
又面,
面面.
若选③,由余弦定理得,,
,又面
面,
又面
面面
(2)因为面,面,
所以,
取中点,则,
所以,又因为,
所以建立如下图所示空间直角坐标系,
,
,
设平面的一个法向量为,
则,即,
令,则,
设平面的一个法向量为,
则,即,
令,则,
,
,
由图可知二面角是钝角,
所以二面角的大小为.
(9),
平面的一个法向量为,
点到平面的距离.
8.(2029·全国·高三专题练习)如图在三棱柱中,为的中点,,.
(1)证明:;
(2)若,且满足:______,______(待选条件).
从下面给出的①②③中选择两个填入待选条件,求二面角的正弦值.
①三棱柱的体积为;
②直线与平面所成的角的正弦值为;
③二面角的大小为60°;
注:若选择不同的组合分别解答,则按第一个解答计分.
【答案】(1)证明见解析
(2)答案见解析
【分析】(1)通过证明平面来证得.
(2)先选择条件,然后根据所选条件,利用几何法或向量法求得二面角的正弦值.
【详解】(1)在三棱柱中,由题意可得,,,
∴,又∵,∴,
同时在中,∵,,∴,
∵平面,
∴平面,
又∵平面,∴.
(2)∵,且,∴平面,
方案一:选择①③
∵平面,∴,,
∴为二面角的平面角,即,
∴,又∵三棱柱的体积为,∴.
法一:取的中点为,连接,,过作于点,连接,
∵平面,∴平面,
又∵,由三垂线定理可得,
∴为二面角的平面角,
其中,,,则,
由于二面角的平面角与二面角的平面角互补,
故二面角的正弦值为.
法二:过作,过作,过作交于点,连接,
∴为二面角的平面角,其中,,,
∴,故二面角的正弦值为.
法三:如图所示,建立空间直角坐标系,
设平面的一个法向量为,且,,
则,令,则,,故,
设平面的一个法向量为,且,,
则,
令,则,,故,
,故二面角的正弦值为.
方案二:选择①②;
解析:过点作于点∵平面平面,,
∴平面,故直线与平面所成角为,且,
设,,则,即,.
余下解法参考方案一.
方案三:选择②③;
∵平面,∴,,
∴为二面角的平面角,即,
过点作于点,
∵平面平面且交线为,,平面,
∴平面,故直线与平面所成角为,且.
设,则,即.
余下解法参考方案一.
9.(2029·甘肃兰州·统考模拟预测)如图所示的五边形中是矩形,,,沿折叠成四棱锥,点是的中点,.
(1)在四棱锥中,可以满足条件①;②;③,请从中任选两个作为补充条件,证明:侧面底面;(注:若选择不同的组合分别解答,则按第一个解答计分.)
(2)在(1)的条件下求直线与平面所成角的正弦值.
【答案】(1)证明见解析
(2)
【分析】(1)选条件①②,利用勾股定理得到,进而得到底面,利用面面垂直的判定定理即可得证;
选条件①③,利用正弦定理得到,进而得到底面,利用面面垂直的判定定理即可得证;
选条件②③,利用余弦定理和勾股定理得到,进而得到底面,利用面面垂直的判定定理即可得证;
(2)由(1)可得平面,建立空间直角坐标系,利用空间向量法计算可得.
【详解】(1)证明:(1)方案一:选条件①②.
因为在四棱锥中,点是的中点,,所以,
又因为在中,,所以,
又因为是矩形,,所以,,
由可得,所以,
则由,,,平面,所以平面,又因为侧面,
所以侧面底面;
方案二:选条件①③.
因为在四棱锥中,点是的中点,,所以,
又因为在中,,
所以由正弦定理得:,即,所以,
即,所以,
则由,,,平面,所以平面,又因为侧面,
所以侧面底面;
方案三:选条件②③.
因为在四棱锥中,点是的中点,,所以,
又因为在中,,所以,
又因为是矩形,,所以,
又因为在中,,则,
设,,
所以有,解得或(舍,所以,
由可得,所以,
则由,,,平面,所以平面,又因为侧面,
所以侧面底面;
(2)在(1)条件下知平面,且,
故如图所示:以为坐标原点,以所在直线为轴,以所在直线为轴,以所在直线为轴,建立空间直角坐标系,
则,,,,
则,,
设平面的法向量为,则,则,
,
设直线与平面所成角为,则,
直线与平面所成角的正弦值为.
10.(2029·全国·高三专题练习)在中,,过点作,交线段于点(如图1),沿将折起,使(如图2),点分别为棱的中点.
(1)求证:;
(2)在①图1中,②图1中,③图2中三棱锥的体积最大.
这三个条件中任选一个,补充在下面问题中,再解答问题.
问题:已知__________,试在棱上确定一点,使得,并求平面与平面的夹角的余弦值.
注:如果选择多个条件分别解答,按第一个解答计分.
【答案】(1)证明见解析
(2).
【分析】(1)根据线面垂直的判定定理与性质可得,结合中位线的性质可得,即可证明;
(2)选①:由二倍角的正切公式求出,进而求出BD,选②:根据向量的线性运算求出BD,选③:设,利用线面垂直的判定定理和性质可得平面,则,利用导数求出体积的最大值,求出BD.分别建立如图空间直角坐标系,利用向量法求出面面角即可;
【详解】(1),平面,
平面平面.
又分别为的中点,
.
(2)选①,在图1所示的中,由,
解得或(舍去).
设,在Rt中,,
解得.
以点为原点,分别为轴建立如图所示的坐标系,
,
则.
设,则.
,即,解得,
当(即是的靠近的一个四等分点)时,.
设平面的一个法向量为,且,
由得令,则,
取平面CBN的一个法向量,
则,
平面BMN与平面的夹角的余弦值为.
选②,在图1所示的中,设,
则,
又,由平面向量基本定理知,即.
以点为原点,分别为轴建立如图所示的空间直角坐标系,
,
则.
设,则,
即,解得,
当(即是的靠近的一个四等分点)时,.
设平面的一个法向量为,且,
由得令,则.
取平面的一个法向量,
则,
平面与平面的夹角的余弦值为.
选③,在图1所示的中,设,则,
为等腰直角三角形,.
折起后,且,平面,
平面,又,
,
令,
当时,;当时,,
时,三棱锥的体积最大.
以点为原点,分别为轴建立如图所示直角坐标系,
,
,则,
设,则.
,即,
解得,
当(即是的靠近的一个四等分点)时,.
设平面的一个法向量为,且,
由得令,则.
取平面的一个法向量,
则,
平面与平面的夹角的余弦值为.
11.(2029·甘肃兰州·统考模拟预测)如图所示的五边形中是矩形,,,沿折叠成四棱锥,点是的中点,.
(1)在四棱锥中,可以满足条件①;②;③,请从中任选两个作为补充条件,证明:侧面底面;(注:若选择不同的组合分别解答,则按第一个解答计分.)
(2)在(1)的条件下求点到平面的距离.
【答案】(1)条件选择见解析,证明见解析
(2)
【分析】(1)选条件①②,利用勾股定理逆定理证得,由等腰三角形的几何性质可得出,利用线面和面面垂直的判定定理可证得结论成立;
选条件 ①③,利用正弦定理推导出,,由等腰三角形的几何性质可得出,利用线面和面面垂直的判定定理可证得结论成立;
选条件②③,利用余弦定理求出的长,利用勾股定理逆定理证得,由等腰三角形的几何性质可得出,利用线面和面面垂直的判定定理可证得结论成立;
(2)计算出三棱锥的体积,计算出的面积,利用等体积法可求得点到平面的距离.
【详解】(1)证明:方案一:选条件①②.
因为在四棱锥中,,点为的中点,则,
因为,在中,,,
又因为四边形为矩形,,则,,
因为,,,所以,,则,
因为,、平面,所以,平面,
因为平面,所以,侧面平面;
方案二:选条件①③.
因为在四棱锥中,,点为的中点,则,
在中,,,,
由正弦定理可得,即,所以,,
所以,,即,
因为,、平面,所以,平面,
因为平面,所以,侧面平面;
方案三:选条件②③.
因为在四棱锥中,,点为的中点,则,且,
在中,,,
又因为四边形为矩形,,则,
所以,,
在中,,则,
设,由余弦定理可得,
整理可得,解得或(舍),所以,,
因为,,,所以,,则,
因为,、平面,所以,平面,
因为平面,所以,侧面平面.
(2)解:在(1)的条件下,平面,
因为为的中点,,,
在中,,,则,
所以,,则,
,
在中,,,则,
所以,,
所以,,
设点到平面的距离为,由可得,
所以,.
因此,点到平面的距离为.
12.(2029·全国·高三专题练习)如图,在四棱锥中,侧棱平面,底面四边形是矩形,,点、分别为棱、的中点,点在棱上.
(1)若,求证:直线平面;
(2)若,从下面①②两个条件中选取一个作为已知,证明另外一个成立.
①平面与平面的交线为直线,与直线成角的余弦值为;
②二面角的余弦值为.
注:若选择不同的组合分别作答,则按第一个解答计分.
【答案】(1)证明见解析
(2)条件选择见解析,证明见解析
【分析】(1)取的中点,连接、,证明出平面平面,利用面面平行的性质可证得结论成立;
(2)若选①,分析可知异面直线与所成的角即为,由结合勾股定理可求得的长,然后以点为坐标原点,、、的方向分别为、、轴的正方向建立空间直角坐标系,利用空间向量法可求得二面角的余弦值;
若选②,以点为坐标原点,、、的方向分别为、、轴的正方向建立空间直角坐标系,设,利用空间向量法可求得的值,分析可知异面直线与所成的角即为,求出的余弦值即可.
【详解】(1)证明:如下图所示,取的中点,连接、,
因为、分别为、的中点,所以,,
因为平面,平面,所以,平面,
又因为,所以,,
因为平面,平面,所以,平面,
因为,、平面,故平面平面,
因为平面,所以,平面.
(2)证明:若选①作为已知条件,平面与平面的交线为直线,作出直线如图,
由于,平面,平面,所以,平面,
因为平面,平面平面,所以,,
所以,异面直线与所成的角即为,
因为,则,则,
故,
以点为坐标原点,、、的方向分别为、、轴的正方向建立如下图所示的空间直角坐标系,
则、、、,,,
设平面的法向量为,则,
取,可得,易知平面的一个法向量为,
则,
由图可知,二面角为锐角,故二面角的余弦值为;
若选②为已知条件,以点为坐标原点,、、的方向分别为、、轴的正方向建立如图所示的空间直角坐标系,
设,则、、,,。
设平面的的法向量为,则,
取,可得,
易知平面的一个法向量为,且二面角的余弦值为,
则,解得,
平面与平面的交线为直线,作出直线如图,
由于,平面,平面,所以,平面,
因为平面,平面平面,所以,,
所以,异面直线与所成的角即为,
因为,则,
则.
19.(2029·江苏盐城·盐城中学校考模拟预测)如图,在四棱锥中,底面ABCD是矩形,底面ABCD,且,E是PC的中点,平面ABE与线段PD交于点F.
(1)证明:F为PD的中点;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线BE与平面PAD所成角的正弦值.
条件①:三角形BCF的面积为;
条件②:三棱锥的体积为1.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】(1)证明见解析
(2)
【分析】(1)由线面平行的判定证面,再由线面平行的性质可证,进而有△中为中位线,即可证结论;
(2)由线面垂直的性质、判定证两两垂直,且面,构建空间直角坐标系,根据所选条件求得,进而求直线方向向量和面的法向量,利用线面角夹角的向量求法求其正弦值.
【详解】(1)由底面ABCD是矩形,则,而面,面,
所以面,
又E是PC的中点,面ABE与线段PD交于点F,即面面,
而面,则,故,
△中为中位线,故F为PD的中点;
(2)由底面ABCD,面,则,又,
由,面,则面,
由面,故,即△为直角三角形,且;
由面,则面面,同理有面面;
又面,故,又,
所以两两垂直,可构建如下空间直角坐标系,
选①,则,故,而,
选②,由,而,所以;
此时,,,则,
又是面的一个法向量,若直线BE与平面PAD所成角为,
所以.
14.(2029·北京·高三专题练习)如图,已知直三棱柱中,,为中点,,再从条件①,条件②这两个条件中选择一个作为已知,完成以下问题:
(1)证明:;
(2)求直线与平面所成角的正弦值.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】(1)证明详见解析
(2)条件选择见解析,直线与平面所成角的正弦值为
【分析】(1)若选①,则通过证明平面来证得.若选②,则先证明,然后通过证明平面来证得.
(2)建立空间直角坐标系,利用向量法求得直线与平面所成角的正弦值.
【详解】(1)若选择条件①:,连接,
在直三棱柱中,平面,平面,
所以.
在三角形中,,为的中点,
所以,由于,平面,
所以平面,由于平面,所以,
由于,,平面,
所以平面,
由于平面,所以.
若选择条件②:,连接,
由于是中点,所以,
根据直三棱柱的性质可知,
由于平面,所以平面,
由于平面,所以.
由于,所以,
所以,则,则,
由于,平面,所以平面,
由于平面,所以.
(2)先得到:
若选①,则在中,由,得,
又,所以,.
若选②,则.
在三角形中,,所以,
所以,
根据直三棱柱的性质可知,,
以点为原点,分别以为轴建立空间直角坐标系,
则,,,,,,
,,,
设平面的法向量为,则,
令,得,
设直线与平面所成角为,
则.
15.(2029·黑龙江哈尔滨·哈九中校考模拟预测)如图,已知四棱锥,底面是平行四边形,且,是线段的中点,.
(1)求证:平面;
(2)下列条件任选其一,求二面角的余弦值.
①与平面所成的角为;
②到平面的距离为.
注:如果选择多个条件分别解答,按一个解答计分.
【答案】(1)证明见解析
(2)
【分析】(1)根据平行四边形中的几何关系可得再根据勾股定理可得,利用线面垂直的判定定理即可证明结果;
(2)选①,取中点为,连接,根据几何关系可得,根据(1)可得,根据线面垂直的判定定理可得平面,则与平面所成的角为,由此计算出,进而计算得,可得为等边三角形;
选②,取中点为,连接,计算长度及根据等体积法可求得,即可得为等边三角形,建立合适的空间直角坐标系,求得各个点的坐标,进而求得平面的法向量及平面的法向量,根据法向量夹角的余弦值的绝对值即为二面角的余弦值绝对值即可求得结果.
【详解】(1)证明:因为,且,故,
在中,,
由余弦定理可得:,
解得,在中,,
所以,即,
又因为平面,平面,
所以平面;
(2)选①,取中点为,连接,如图所示:
因为,故,由(1)得平面,
因为平面,所以,
因为,平面,平面,
所以平面,所以为与平面所成的角,
即,因为,,
所以为等边三角形,且边长为1,所以,,
由可得,
因为,,
所以,所以为等边三角形,
以为原点,为在轴正方向建立如图所示空间直角坐标系:
所以,
,
设是平面的法向量,
则,即,
取,可得,
设为平面的法向量,
则,即,
取,可得,
设二面角所成的角为,则,
所以二面角的余弦值为.
选②, 取中点为,连接,如图所示:
因为,故,由(1)得平面,
因为平面,所以,
因为,平面,平面,所以平面,
设到平面的距离为,
因为,,所以等边三角形,
所以,,设,则,
因为,所以,
因为,为中点,所以,
所以,由,,
平面,平面,所以平面,
因为平面,所以,即,
所以,因为,
即,
即,
解得,即,所以,所以为等边三角形,
以为原点,为在轴正方向建立如图所示空间直角坐标系:
所以,
,
设是平面的法向量,
则,即,
取,可得,
设为平面的法向量,
则,即,
取,可得,
设所成的角为,则,
所以二面角的余弦值为.
16.(2029·江苏·统考三模)如图,三棱锥P-ABC的底面为等腰直角三角形,∠ABC=90°,AB=2.D,E分别为AC,BC的中点,PD⊥平面ABC,点M在线段PE上.
(1)再从条件①、②、③、④四个条件中选择两个作为已知,使得平面MBD⊥平面PBC,并给予证明;
(2)在(1)的条件下,求直线BP与平面MBD所成的角的正弦值.
条件①:;
条件②:∠PED=60°;
条件③:PM=9ME:
条件④:PE=9ME.
【答案】(1)答案见解析
(2)答案见解析
【分析】(1)如图,建立以D为原点的空间直角坐标系,设,,由平面MBD⊥平面PBC,可得两平面法向量互相垂直,即可得,据此可知可选择①④或②③;
(2)由(1)所建立空间直角坐标系及平面MBD法向量,利用向量方法可得答案.
【详解】(1)因PD⊥平面ABC,平面ABC,平面ABC,则,
又由题可知,则如图,建立以D为原点的空间直角坐标系,
则,,,,
设,.
则,,,,.
故.
设平面MBD法向量为,
则,令,可得;
设平面PBC法向量为,
则,可令,可得.
要使平面MBD⊥平面PBC,需满足.
注意到条件①,
PD⊥平面ABC,平面ABC,,又由题可知,则条件②,
条件③,条件④.
则当条件①④成立或条件②③成立时,都有,即可以使平面MBD⊥平面PBC;
(2)由(1),当选择①④时,,,.
则,平面MBD法向量为,
设BP与平面MBD所成角为,则;
当选择②③时,,,.
则,平面MBD法向量,
设BP与平面MBD所成角为,则;
.
21世纪教育网(www.21cnjy.com)
同课章节目录
