第三单元《分数除法》(应用题篇四大题型)单元复习讲义(知识梳理+典例精讲+专项精练)-2024-2025学年六年级数学上册(人教版)(学生版+解析)
文档属性
| 名称 | 第三单元《分数除法》(应用题篇四大题型)单元复习讲义(知识梳理+典例精讲+专项精练)-2024-2025学年六年级数学上册(人教版)(学生版+解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 980.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-08 20:12:31 | ||
图片预览





文档简介
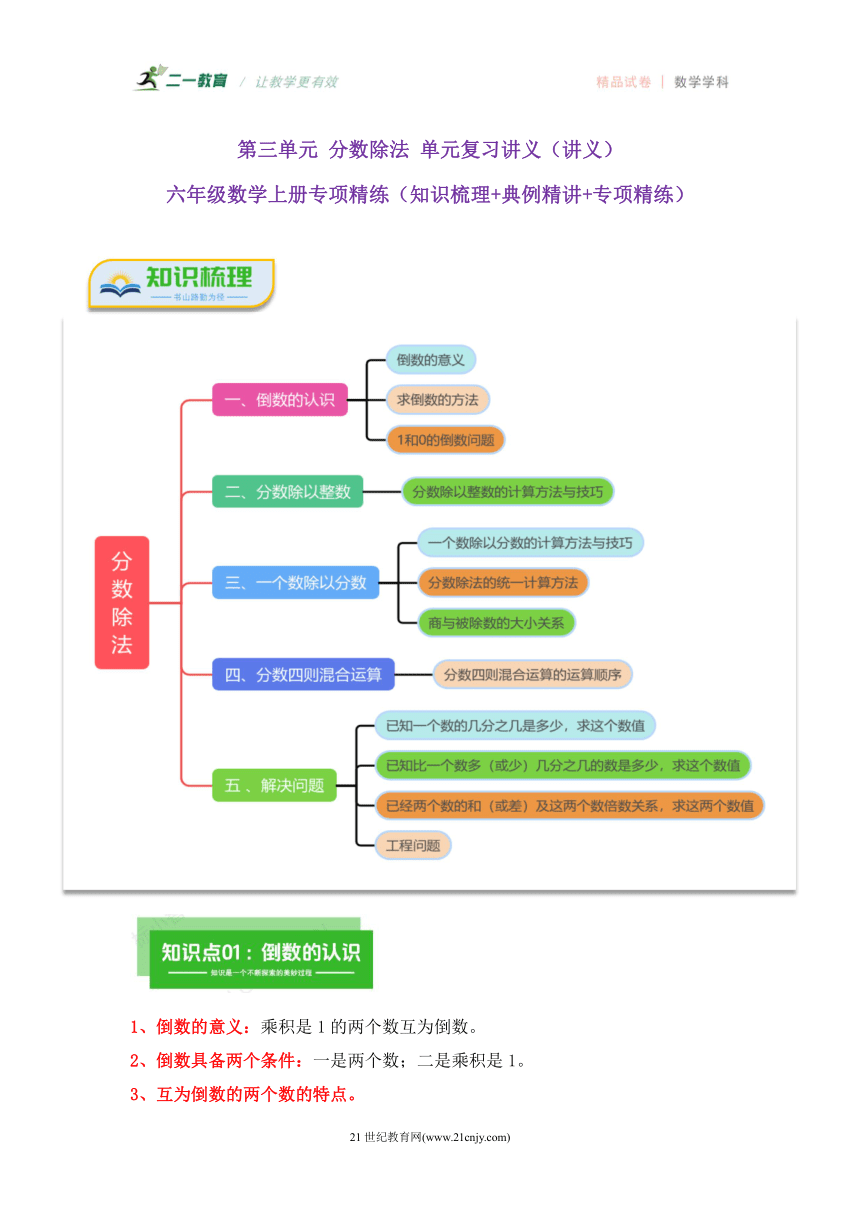
第三单元 分数除法 单元复习讲义(讲义)
六年级数学上册专项精练(知识梳理+典例精讲+专项精练)
1、倒数的意义:乘积是1的两个数互为倒数。
2、倒数具备两个条件:一是两个数;二是乘积是1。
3、互为倒数的两个数的特点。
(1)如果两个数都是分数,那么两个分数的分子和分母正好颠倒了位置;
(2)如果一个是整数,则另一个分数的分子是1,分母是这个整数。
4、求一个数的倒数的方法。
(1)求一个分数的倒数,把这个分数的分子、分母交换位置即可;
(2)求小数的倒数,先把小数化成分数,再求倒数;
(3)求非0整数的倒数,让这个整数作分母,分子是1。
5、注意事项:
(1)1的倒数是1,等于它本身;
(2)0没有倒数。
6、易错点:
(1)易错点在于混淆倒数定义。记住,乘积为1的两个数互为倒数,如5的倒数是 。计算时,常错将分子分母颠倒而不求其积为1,如误将 的倒数写为 的相反数。务必理解并准确应用倒数概念。
1、分数除以整数的计算方法。
(1)当一个分数被除以一个非零整数时,其结果等同于该分数乘以该整数的倒数。
在数学运算中,当遇到分子能够被某个整数整除的情况时,应采取以下步骤进行化简:将原分子除以该整数,并将所得的商作为新的分子,而分母则保持不变。这一操作确保了分数的等价性,同时简化了其表达形式。
2、一个数除以分数。
(1) 整数除以分数的计算方法:整数除以分数,用这个整数乘这个分数的倒数。
(2)分数除以分数的计算方法:分数除以分数,用被除数乘除数的倒数。
(3)分数除法的一般方法:一个数除以一个不等于0的数,等于乘这个数的倒数。
3、被除数与商的变化规律。
(1)除以大于 1 的数,商小于被除数:a÷b=c 当b>1时,c<a (a≠0);
(2)除以小于 1 的数,商大于被除数:a÷b=c 当b<1时,c>a (a≠0,b≠0);
(3)除以等于 1 的数,商等于被除数:a÷b=c 当b=1时,c=a。
4、易错点:分数除法时,易混淆除数与被除数位置,将分数除以整数误变为倒数相乘。同时,解题时易忽视找单位“1”,导致等量关系错误。此外,还需注意混合运算顺序,以及理解分数除法与乘法的互逆关系。
1、情况一:在进行同级运算时,应当严格遵循从左至右的顺序进行计算。
2、情况二:在进行数学运算时,若未涉及小括号,则需遵循既定的运算优先级规则,即先进行乘除运算,随后再执行加减运算。
3、情况三:在进行数学运算时,若表达式中包含小括号,则应首先计算小括号内的运算,待小括号内的运算完成后,再进行小括号外的运算。这是数学运算的基本规则之一,旨在确保运算的准确性和逻辑性。
4、易错点:混淆运算顺序,如先加减后乘除;忽视括号优先级,去括号时符号出错;错用运算律,如乘法分配律误用于除法;对分数意义理解不足,导致计算错误。需特别注意运算规则与分数性质,确保计算准确。
1、“已知一个数的几分之几是多少,求这个数”的方法:
已知量÷已知量占单位“1”的几分之几=单位“1”的量;
2、“已知比一个数多(或少)几分之几的数是多少,求这个数”的方法:
单位“1”的量×(1±几分之几)=已知量
单位“1”的量±单位“1”的量×几分之几=已知量
3、“已知两个量的和(差),其中一个量是另一个量的几分之几,求这两个量”的问题的解法:
有两个量都是未知的,先把谁看作单位“1”都可以,再用方程法求解:
(1)找出单位“1”,设未知量为x;
(2)找出题中的等量关系式;
(3)列出方程并解答;
(4)检验并写出答案。
4、工程问题。
(1)工作时间=工作总量÷工作效率
(2)利用抽象的“1”解决实际问题:
工程问题是分数问题的特例,工作总量与工作效率都不是具体的数,而是用抽象的分数来表示。一般地,工作总量用单位“1”来表示,工作效率则用完成总量所需时间的倒数来表示。
5、易错点:易错点在于混淆了乘除法的应用情境。例如,在涉及单价、数量、总价和工程的问题中,学生可能错误地将单价乘以数量视为总价,或反过来用总价除以数量得到单价,导致计算结果错误。此外,未准确理解题目中的比例关系也是常见错误。因此,审题需细致,理解题意后再选择正确算法,完成解题后,务必结合实际推理检验。
【典例精讲1】.“a是一个整数,它的倒数一定是。”这句话对吗?请说明理由。
【答案】解:这句话不对。如果a是0,0也是整数,但0没有倒数。
【解析】【分析】求一个数(0除外)的倒数=1÷这个数,因为0不能作除数,所以和这个数不能是0。
【典例精讲2】.(2023-2024-2024六上·万载月考)一根m 长的钢管重 10kg,这种钢管每米重多少千克?每千克钢管有多少米?
【答案】解:10÷=16(千克)
÷10=(米)
答:这种钢管每米重16千克,每千克钢管有米。
【解析】【分析】这种钢管每米重的质量=总质量÷这种钢管的长度;每千克钢管的长度=总长度÷总质量。
【典例精讲3】.(2023-2024-2024六上·五华月考)一个制药厂每天可以提炼t药材,现因业务需要,计划提炼t药材。则提炼这批药材需要多少天?
【答案】解: =7.5(天)
答:提炼这批药材需要7.5天。
【解析】【分析】提炼这批药材需要的天数=提炼药材的总质量÷平均每天提炼药材的质量。
【典例精讲4】.(2023-2024-2024六上·易门月考)一罐千克的奶粉,小峰最多可以喝几天,最少可以喝几天?
【答案】解:=7(天)
=3.5(天)
答:小峰最多可以喝7天,最少可以喝3.5天。
【解析】【分析】小峰最多可以喝的天数=一罐奶粉的质量÷小峰每天最少喝的质量,小峰最少可以喝的天数=一罐奶粉的质量÷小峰每天最多喝的质量,据此代入数值作答即可。
【典例精讲5】.(2023-2024-2024六上·期末)学校图书室里有故事书有390本,比科技书的本数多。学校图书室里有多少本科技书?
【答案】解:390÷(1+)
=390÷
=390×
=240(本)
答:学校图书室里有240本科技书。
【解析】【分析】将科技书的本数看作单位“1”,则故事书的本数是科技书的1+,求单位“1”用除法。科技书的本数=故事书的本数÷故事书的本数是科技书的几分之几。
【典例精讲6】.(2023-2024-2024六上·钱塘)美丽乡村建设时,某工程队修一条路,第二天修的长度是第一天的,两天一共修了600米,则第二天比第一天少修多少米?
【答案】解:600÷(1+ )
=600÷
=320 (米)
600-320=280 (米)
320-280=40 (米)
答:则第二天比第一天少修40米。
【解析】【分析】把第一天修的长度看成单位“1”,所以第一天修的长度=两天一共修的长度÷两天一共修了几分之几,第二天修的长度=两天一共修的长度-第一天修的长度,那么第二天比第一天少修的长度=第一天修的长度-第二天修的长度,据此代入数值作答即可。
【典例精讲7】.(2023-2024-2024六上·金乡县期中)一段路长 3600米,甲工程队单独修需要30天完成,乙工程队单独修需要45天,两队合修几天可修这条路的三分之二?
【答案】解:3600×=2400(米)
3600÷30=120(米)
3600÷45=80(米)
2400÷(120+80)
=2400÷200
=12(天)
答:两队合修12天可修这条路的三分之二。
【解析】【分析】这条路的三分之二的长度=这条路的长度×,甲工程队每天修的长度=这条路的长度÷甲工程队单独修完需要的天数,乙工程队每天修的长度=这条路的长度÷乙工程队单独修完需要的天数,那么两队合修完成这条路的三分之二需要的天数=这条路的三分之二的长度÷两工程队每天一共修的长度,据此代入数值作答即可。
应用题。
一本故事书,小瑞第一天看了第二天看了刚好看到第60页,这本书有多少页
2.(2023-2024六上·英山期末)新洲小学购买一批图书,其中科技书有280本,正好是这批图书的,这批图书一共有多少本?
3.(2023-2024六上·凉州期末)一杯250毫升的鲜牛奶含有克的钙质,占一个成年人一天所需钙质的。一个成年人一天需要多少钙质?
4.(2023-2024六上·余杭月考)某工程队修一条长500米的公路,5天后,未修的公路长度是已修公路长度的。工程队已经修了多少米?
5.(2023-2024六上·阳春期中)六年级男生比女生多60人,女生人数是男生人数的,六年级男、女生各有多少人?
6.(2023-2024六上·阳春期中)一辆汽车以每小时45千米的速度从甲地到乙地,3小时行了全程的,这辆汽车还要行多少千米才能到达乙地?
7.(2023-2024六上·斗门期中)小东看一本科技书,已经看了210页,占全书页数的 。这本科技书有多少页?(先用线段图表示题中数量关系,再解答)。
(2023-2024六上·龙岗期中)某工厂九月份用水30吨,九月份比十月份多用水,十月份用多少吨?
9.狮子奔跑时的最高速度可以达到60千米/时,比猎豹奔跑时的最高速度慢。猎豹奔跑时的最高速度是多少?
10.(2023-2024六上·永福期中) 小宇的体重是42千克,小宇的体重比爸爸的体重轻,爸爸的体重是多少千克?
11.(2023-2024六上·红安期中)一项工程,甲单独做20天完成,乙单独做用30天完成。甲、乙两队合修3天后,雨下的由乙队做,需要多少天才能完成?
12.(2023-2024六上·张湾期中)六年级同学为学校图书馆整理图书,他们已经整理了300本,还剩没有整理。需要整理的图书一共有多少本?
13.(2023-2024六上·张湾期中)服装厂接到一批订单,第一车间单独做需要10天完成,第二车间单独做3天完成了,如果两个车间同时做这批订单,多少天可以完成这批订单?
14.(2023-2024六上·监利期中)一辆货车从甲地开往乙地,已行全程的,距中点还有25千米,甲乙两地相距多少千米?
15.(2023-2024六上·鄂城期中)某工厂全部改用节能LED灯具后,现在每月照明用电量是185千瓦时,比原来每月节约,原来每月用电量是多少千瓦时?
16.(2023-2024六上·涟源期中)李老师从新化开车去长沙,行了全程的后,还剩下90km没有行,从新化到长沙共有多少千米?
17.(2023-2024六上·新田期中) 一项工程,甲单独做8天可以完成,乙单独做6天可以完成。
(1)甲乙合作一起完成,需要多少天?
(2)如果由乙先做3天,剩下的由甲来做,还需要多少天能完成这项工程?
(2023-2024六上·慈利期中)国庆节布置教室,六⑴班一共需要做320朵黄花,其中黄花的朵数是红花朵数的,红花比黄花多多少朵?
19.张师傅带了一些钱去购买办公桌椅。这些钱如果全部用来购买桌子,可以买20张;如果全部用来购买椅子,可以买30把。这些钱可以买多少套办公桌椅?(一张桌子和一把椅子是1套)
20.(2023-2024六上·黔江期末) 水果批发市场新进一批水果,运来苹果3吨,比运来橘子的少0.2吨,运来橘子多少吨?
21.一年好景君须记,最是橙黄橘绿时”,果园里橘子大丰收了!今年王奶奶还尝试了“直播带货”,销量大增,一共卖出了3500千克,其中通过直播卖出的橘子数量是线下的。线上直播卖出了多少千克
22.为迎接新年,实验小学六(3)班布置教室,买了一个大灯笼和12个小灯笼,一共花费112元.已知一个小灯笼是一个大灯笼单价的。小灯笼和大灯笼的单价各是多少元
23.一项工程,甲队单独做10天完成,乙队的工作效率是甲队的。如果甲、乙两队合做,几天可以完成这项工程的?
24.(2023-2024六上·新田期末)果园里有苹果树120棵。桃树的棵树是苹果树的,还是梨树的,果园里有梨树多少棵?
25.(2023-2024六上·淮滨月考)十一假期期间,聪聪一家开车去鸡公山景区游玩,小时行驶了90千米,正好是全程的。
(1)聪聪从家到鸡公山景区有多少千米
(2)聪聪从家开车到鸡公山景区一共需要多少小时
26.(2023-2024六上·淮滨月考)实验小学足球社团有54人,是舞蹈社团人数的,比合唱社团的人数少,舞蹈社团和合唱社团各有多少人?
27.(2023-2024六上·阳春期中)修一条公路,甲队单独修要15天完成,乙队单独修要20天完成,甲乙两队一起修了6天后,甲队有事离开了,由乙队单独修完,乙队还需要多少天?
28.筑路队修一条10千米的公路.第一天修了全长的 ,第二天修了 千米,还有多少千米没有修?
29.(2023-2024六上·天河期末)冬至是一年中白昼最短、黑夜最长的一天。这一天,某地的白昼时间是黑夜时间的 ,该地冬至的白昼时间是多少小时?
30.(2023-2024六上·岑巩期中)开学初, 阳光小学共有 84 名同学参加了少先队大队委的竞选活动。其中女生人数是男生人数的 , 参加竞选活动的男生、女生各有多少人?
31.(2023-2024六上·播州期中)小军看一本故事书, 第一周看了全书的 , 第二周看了余下的 , 还剩 75 页没有读, 这本故事书有多少页
32.(2023-2024六上·张湾期中)一辆大巴从A地出发,以80千米每时的速度行驶,6小时到达B地,如果大巴速度再快,几小时可到达B地?
33.(2023-2024六上·鄂城期中)迎宾大道铺沥青,工程队每天修千米,8天后,还剩下全长的,迎宾大道全长多少千米?
34.(2023-2024六上·桂林月考)书的人类进步的阶梯,天天小学举行“读书增智”的活动,活动期间,明明读一本名人传记,第一天读了全书的,第二天读了余下的,还剩60页没有读,这本名人传记共有多少页?
35.(2023-2024六上·播州期中)某救援小队奉命为灾区运送救灾物资,救援小队已经行驶了全程的,如果再行驶15km,那么就行驶了全程的一半。救援小队的出发地距离灾区多少千米
36.(2023-2024六上·邢台期中)学校安排六年级学生做小红旗,六⑴班做了60面小红旗,比六⑵班少做了,你能算出六⑴班比六⑵班同学少做了多少面小红旗吗?
37.(2023-2024六上·邢台期中)甲、乙两个修路队合修一条路,甲队已经修了40千米,乙队已经修了44千米,乙队修的比甲队修的多这条路的,这条路全长多少千米?
38.在某大坝截流时,用载重卡车将一堆石料运到围堰龙口,第一次运了这堆石料的少2万方,第二次运了剩下的多3万方,此时还剩下12万方未运,则这堆石料共有多少万方?
39.(2023-2024六上·莲湖期末)某路段为了防止内涝,需要挖一条1200 米长的下水道,第一周挖了总长的 ,比第二周挖的长度短 ,第二周挖了多少米?
40.(2023-2024六上·平果期中)希望小学即将迎来10周华校庆,六⑴班准备召开校庆联欢会,小江和小南负资布置教室。小江单独挂彩条,需要12分钟:小南单独挂彩条,需要24分钟。
(1)如果两人合作挂彩条需要多长时间
(2)如果两人合作4分钟后,小南去摆桌椅,由小江单独挂剩下的彩条,还需要多长时问才能把彩条排好
21世纪教育网(www.21cnjy.com)
第三单元 分数除法 单元复习讲义(讲义)
六年级数学上册专项精练(知识梳理+典例精讲+专项精练)
1、倒数的意义:乘积是1的两个数互为倒数。
2、倒数具备两个条件:一是两个数;二是乘积是1。
3、互为倒数的两个数的特点。
(1)如果两个数都是分数,那么两个分数的分子和分母正好颠倒了位置;
(2)如果一个是整数,则另一个分数的分子是1,分母是这个整数。
4、求一个数的倒数的方法。
(1)求一个分数的倒数,把这个分数的分子、分母交换位置即可;
(2)求小数的倒数,先把小数化成分数,再求倒数;
(3)求非0整数的倒数,让这个整数作分母,分子是1。
5、注意事项:
(1)1的倒数是1,等于它本身;
(2)0没有倒数。
6、易错点:
(1)易错点在于混淆倒数定义。记住,乘积为1的两个数互为倒数,如5的倒数是 。计算时,常错将分子分母颠倒而不求其积为1,如误将 的倒数写为 的相反数。务必理解并准确应用倒数概念。
1、分数除以整数的计算方法。
(1)当一个分数被除以一个非零整数时,其结果等同于该分数乘以该整数的倒数。
在数学运算中,当遇到分子能够被某个整数整除的情况时,应采取以下步骤进行化简:将原分子除以该整数,并将所得的商作为新的分子,而分母则保持不变。这一操作确保了分数的等价性,同时简化了其表达形式。
2、一个数除以分数。
(1) 整数除以分数的计算方法:整数除以分数,用这个整数乘这个分数的倒数。
(2)分数除以分数的计算方法:分数除以分数,用被除数乘除数的倒数。
(3)分数除法的一般方法:一个数除以一个不等于0的数,等于乘这个数的倒数。
3、被除数与商的变化规律。
(1)除以大于 1 的数,商小于被除数:a÷b=c 当b>1时,c<a (a≠0);
(2)除以小于 1 的数,商大于被除数:a÷b=c 当b<1时,c>a (a≠0,b≠0);
(3)除以等于 1 的数,商等于被除数:a÷b=c 当b=1时,c=a。
4、易错点:分数除法时,易混淆除数与被除数位置,将分数除以整数误变为倒数相乘。同时,解题时易忽视找单位“1”,导致等量关系错误。此外,还需注意混合运算顺序,以及理解分数除法与乘法的互逆关系。
1、情况一:在进行同级运算时,应当严格遵循从左至右的顺序进行计算。
2、情况二:在进行数学运算时,若未涉及小括号,则需遵循既定的运算优先级规则,即先进行乘除运算,随后再执行加减运算。
3、情况三:在进行数学运算时,若表达式中包含小括号,则应首先计算小括号内的运算,待小括号内的运算完成后,再进行小括号外的运算。这是数学运算的基本规则之一,旨在确保运算的准确性和逻辑性。
4、易错点:混淆运算顺序,如先加减后乘除;忽视括号优先级,去括号时符号出错;错用运算律,如乘法分配律误用于除法;对分数意义理解不足,导致计算错误。需特别注意运算规则与分数性质,确保计算准确。
1、“已知一个数的几分之几是多少,求这个数”的方法:
已知量÷已知量占单位“1”的几分之几=单位“1”的量;
2、“已知比一个数多(或少)几分之几的数是多少,求这个数”的方法:
单位“1”的量×(1±几分之几)=已知量
单位“1”的量±单位“1”的量×几分之几=已知量
3、“已知两个量的和(差),其中一个量是另一个量的几分之几,求这两个量”的问题的解法:
有两个量都是未知的,先把谁看作单位“1”都可以,再用方程法求解:
(1)找出单位“1”,设未知量为x;
(2)找出题中的等量关系式;
(3)列出方程并解答;
(4)检验并写出答案。
4、工程问题。
(1)工作时间=工作总量÷工作效率
(2)利用抽象的“1”解决实际问题:
工程问题是分数问题的特例,工作总量与工作效率都不是具体的数,而是用抽象的分数来表示。一般地,工作总量用单位“1”来表示,工作效率则用完成总量所需时间的倒数来表示。
5、易错点:易错点在于混淆了乘除法的应用情境。例如,在涉及单价、数量、总价和工程的问题中,学生可能错误地将单价乘以数量视为总价,或反过来用总价除以数量得到单价,导致计算结果错误。此外,未准确理解题目中的比例关系也是常见错误。因此,审题需细致,理解题意后再选择正确算法,完成解题后,务必结合实际推理检验。
【典例精讲1】.“a是一个整数,它的倒数一定是。”这句话对吗?请说明理由。
【答案】解:这句话不对。如果a是0,0也是整数,但0没有倒数。
【解析】【分析】求一个数(0除外)的倒数=1÷这个数,因为0不能作除数,所以和这个数不能是0。
【典例精讲2】.(2023-2024-2024-2024六上·万载月考)一根m 长的钢管重 10kg,这种钢管每米重多少千克?每千克钢管有多少米?
【答案】解:10÷=16(千克)
÷10=(米)
答:这种钢管每米重16千克,每千克钢管有米。
【解析】【分析】这种钢管每米重的质量=总质量÷这种钢管的长度;每千克钢管的长度=总长度÷总质量。
【典例精讲3】.(2023-2024-2024-2024六上·五华月考)一个制药厂每天可以提炼t药材,现因业务需要,计划提炼t药材。则提炼这批药材需要多少天?
【答案】解: =7.5(天)
答:提炼这批药材需要7.5天。
【解析】【分析】提炼这批药材需要的天数=提炼药材的总质量÷平均每天提炼药材的质量。
【典例精讲4】.(2023-2024-2024-2024六上·易门月考)一罐千克的奶粉,小峰最多可以喝几天,最少可以喝几天?
【答案】解:=7(天)
=3.5(天)
答:小峰最多可以喝7天,最少可以喝3.5天。
【解析】【分析】小峰最多可以喝的天数=一罐奶粉的质量÷小峰每天最少喝的质量,小峰最少可以喝的天数=一罐奶粉的质量÷小峰每天最多喝的质量,据此代入数值作答即可。
【典例精讲5】.(2023-2024-2024-2024六上·期末)学校图书室里有故事书有390本,比科技书的本数多。学校图书室里有多少本科技书?
【答案】解:390÷(1+)
=390÷
=390×
=240(本)
答:学校图书室里有240本科技书。
【解析】【分析】将科技书的本数看作单位“1”,则故事书的本数是科技书的1+,求单位“1”用除法。科技书的本数=故事书的本数÷故事书的本数是科技书的几分之几。
【典例精讲6】.(2023-2024-2024-2024六上·钱塘)美丽乡村建设时,某工程队修一条路,第二天修的长度是第一天的,两天一共修了600米,则第二天比第一天少修多少米?
【答案】解:600÷(1+ )
=600÷
=320 (米)
600-320=280 (米)
320-280=40 (米)
答:则第二天比第一天少修40米。
【解析】【分析】把第一天修的长度看成单位“1”,所以第一天修的长度=两天一共修的长度÷两天一共修了几分之几,第二天修的长度=两天一共修的长度-第一天修的长度,那么第二天比第一天少修的长度=第一天修的长度-第二天修的长度,据此代入数值作答即可。
【典例精讲7】.(2023-2024-2024-2024六上·金乡县期中)一段路长 3600米,甲工程队单独修需要30天完成,乙工程队单独修需要45天,两队合修几天可修这条路的三分之二?
【答案】解:3600×=2400(米)
3600÷30=120(米)
3600÷45=80(米)
2400÷(120+80)
=2400÷200
=12(天)
答:两队合修12天可修这条路的三分之二。
【解析】【分析】这条路的三分之二的长度=这条路的长度×,甲工程队每天修的长度=这条路的长度÷甲工程队单独修完需要的天数,乙工程队每天修的长度=这条路的长度÷乙工程队单独修完需要的天数,那么两队合修完成这条路的三分之二需要的天数=这条路的三分之二的长度÷两工程队每天一共修的长度,据此代入数值作答即可。
应用题。
1.一本故事书,小瑞第一天看了第二天看了刚好看到第60页,这本书有多少页
【答案】解:60÷(+)
=60÷
=175(页)
答:这本书有175页。
【解析】【分析】这本书的总页数=已经看的页数÷(第一天看的分率+第二天看的分率)。
2.(2023-2024六上·英山期末)新洲小学购买一批图书,其中科技书有280本,正好是这批图书的,这批图书一共有多少本?
【答案】解:280÷=2450(本)
答:这批图书一共有2450本。
【解析】【分析】根据题意,把这批图书的总本数看作单位“1”,求单位“1”用除法计算,科技书的本数÷科技书占图书的=图书的总本数,据此列式解答。
3.(2023-2024六上·凉州期末)一杯250毫升的鲜牛奶含有克的钙质,占一个成年人一天所需钙质的。一个成年人一天需要多少钙质?
【答案】解:÷ =(千克)
答:一个成年人一天需要 克钙质。
【解析】【分析】一个成年人一天需要钙质的质量=一杯250毫升的鲜牛奶中钙质的质量÷一个成年人一天所需钙质的分率。
4.(2023-2024六上·余杭月考)某工程队修一条长500米的公路,5天后,未修的公路长度是已修公路长度的。工程队已经修了多少米?
【答案】解:500÷(1+)
=500÷
=312.5(米)
答:工程队已经修了312.5米。
【解析】【分析】工程队已经修的米数=这条公路的总长÷(1+)。
5.(2023-2024六上·阳春期中)六年级男生比女生多60人,女生人数是男生人数的,六年级男、女生各有多少人?
【答案】解:60÷(1- )
=60÷
=600(人)
600+60=660(人)
答:六年级男生660人,女生600人。
【解析】【分析】六年级女生人数=六年级男生比女生多的人数÷(1-) ,六年级男生人数=六年级女生人数+多的60人。
6.(2023-2024六上·阳春期中)一辆汽车以每小时45千米的速度从甲地到乙地,3小时行了全程的,这辆汽车还要行多少千米才能到达乙地?
【答案】解:45×3÷ -45×3
=189-135
=54(千米)
答:这辆汽车还要行54千米才能到达乙地。
【解析】【分析】到达乙地这辆汽车还要行驶的路程=这辆汽车的速度×行驶的时间÷已经行驶的路程- 这辆汽车的速度×行驶的时间。
7.(2023-2024六上·斗门期中)小东看一本科技书,已经看了210页,占全书页数的 。这本科技书有多少页?(先用线段图表示题中数量关系,再解答)。
【答案】解:
210÷ =490(页)
答:这本科技书有490页。
【解析】【分析】这本科技书的页数=已经看的页数÷所占的百分率。
8.(2023-2024六上·龙岗期中)某工厂九月份用水30吨,九月份比十月份多用水,十月份用多少吨?
【答案】解:30÷(1+ )
=30÷
=25(吨)
答:十月份用水25吨。
【解析】【分析】十月份用水的吨数=九月份用水的吨数÷(1+多的分率)。
9.狮子奔跑时的最高速度可以达到60千米/时,比猎豹奔跑时的最高速度慢。猎豹奔跑时的最高速度是多少?
【答案】解:60÷(1-)
=60÷
=110(千米/时)
答:猎豹奔跑时的最高速度是110千米/时。
【解析】【分析】猎豹奔跑时的最高速度=狮子奔跑时的最高速度÷(1-慢的分率)。
10.(2023-2024六上·永福期中) 小宇的体重是42千克,小宇的体重比爸爸的体重轻,爸爸的体重是多少千克?
【答案】解:42÷(1-)
=42÷
=70(千克)
答:爸爸的体重是70千克。
【解析】【分析】爸爸的体重=小宇的体重÷(1-轻的分率)。
11.(2023-2024六上·红安期中)一项工程,甲单独做20天完成,乙单独做用30天完成。甲、乙两队合修3天后,雨下的由乙队做,需要多少天才能完成?
【答案】解:
=
=
=
=22.5(天)
答:需要22.5天才能完成
【解析】【分析】根据题目可知,甲的工作效率是,乙的工作效率是, 把这项工程看作单位“1”,用单位“1”减去甲、乙两队合作3天的工作量,得出剩下的工作总量,剩下的工作总量除以乙的工作效率即可求出需要的时间。
12.(2023-2024六上·张湾期中)六年级同学为学校图书馆整理图书,他们已经整理了300本,还剩没有整理。需要整理的图书一共有多少本?
【答案】解:300÷(1)
=300
=750(本)
答:需要整理的图书一共有750本。
【解析】【分析】已经整理的本数÷已经整理的本数占 需要整理的图书的分率= 需要整理的图书的本数。
13.(2023-2024六上·张湾期中)服装厂接到一批订单,第一车间单独做需要10天完成,第二车间单独做3天完成了,如果两个车间同时做这批订单,多少天可以完成这批订单?
【答案】解:1÷()
=1÷(+)
=1
=6(天)
答:6天可以完成。
【解析】【分析】工作总量1÷第一车间单独做需要的时间=第一车间的工作效率;第二车间单独做3天完成的工作效率÷3=第二车间的工作效率;单位1÷两个车间的工作效率之和=完成这批订单需要的时间。
14.(2023-2024六上·监利期中)一辆货车从甲地开往乙地,已行全程的,距中点还有25千米,甲乙两地相距多少千米?
【答案】解:25÷()
=25÷
=250(千米)
答:甲、乙两地相距250千米。
【解析】【分析】中点就是全程的,用减去求出距离中点的分率,根据分数除法的意义,用距离中点的长度除以距离中点的分率即可求出两地的距离。
15.(2023-2024六上·鄂城期中)某工厂全部改用节能LED灯具后,现在每月照明用电量是185千瓦时,比原来每月节约,原来每月用电量是多少千瓦时?
【答案】解:185÷(1-)
=185÷
=259(千瓦时)
答:原来每月用电量是259千瓦时。
【解析】【分析】原来每月用电量=现在每月用电量÷(1-节约的分率)。
16.(2023-2024六上·涟源期中)李老师从新化开车去长沙,行了全程的后,还剩下90km没有行,从新化到长沙共有多少千米?
【答案】解:90÷(1﹣)
=90÷
=225(千米)
答:从新化到长沙共有225千米。
【解析】【分析】90千米÷90千米对应全程的分率=全程。
17.(2023-2024六上·新田期中) 一项工程,甲单独做8天可以完成,乙单独做6天可以完成。
(1)甲乙合作一起完成,需要多少天?
(2)如果由乙先做3天,剩下的由甲来做,还需要多少天能完成这项工程?
【答案】(1)解:1÷8=,1÷6=
1÷(+)
=1÷
=(天)
答:需要天。
(2)解:(1-×3)÷
=×8
=4(天)
答:还需要4天能完成这项工程。
【解析】【分析】(1)把这项工程看成单位“1”,那么需要的天数=1÷甲、乙两人每天一共完成几分之几;
(2)乙先做3天,剩下几分之几=1-乙每天完成几分之几×3,那么还要的天数=剩下几分之几÷甲每天完成几分之几,据此代入数值作答即可。
18.(2023-2024六上·慈利期中)国庆节布置教室,六⑴班一共需要做320朵黄花,其中黄花的朵数是红花朵数的,红花比黄花多多少朵?
【答案】解:320÷-320
=400-320
=80(朵)
答:红花比黄花多80朵。
【解析】【分析】 黄花的朵数 ÷ 黄花的朵数占红花朵数的分率=红花朵数,红花朵数-黄花的朵数=红花比黄花多的朵数。
19.张师傅带了一些钱去购买办公桌椅。这些钱如果全部用来购买桌子,可以买20张;如果全部用来购买椅子,可以买30把。这些钱可以买多少套办公桌椅?(一张桌子和一把椅子是1套)
【答案】解:1÷(+)
=1÷
=12(套)
答:这些钱可以买12套办公桌椅。
【解析】【分析】把总钱数看作单位“1”,那么一张桌子的钱数就占总钱数的,一把椅子的钱数就占总钱数的;一套桌椅的钱数就占总钱数的(+),用单位“1”除以一套桌椅的分率即可解答。
20.(2023-2024六上·黔江期末) 水果批发市场新进一批水果,运来苹果3吨,比运来橘子的少0.2吨,运来橘子多少吨?
【答案】解:(3+0.2)÷
=3.2÷
=3.2×
=3.6(吨)
答:运来橘子3.6吨。
【解析】【分析】苹果比运来橘子的少0.2吨,说明橘子的是(3+0.2)吨,已知一个数的几分之几是多少,求这个数,用乘法。
21.一年好景君须记,最是橙黄橘绿时”,果园里橘子大丰收了!今年王奶奶还尝试了“直播带货”,销量大增,一共卖出了3500千克,其中通过直播卖出的橘子数量是线下的。线上直播卖出了多少千克
【答案】解:3500÷(1+)×
=3500÷×
=2000×
=1500(千克)
答:线上直播卖出了1500千克。
【解析】【分析】线上直播卖出的质量=卖出的总质量÷(1+线上直播占的分率)×线上直播占的分率。
22.为迎接新年,实验小学六(3)班布置教室,买了一个大灯笼和12个小灯笼,一共花费112元.已知一个小灯笼是一个大灯笼单价的。小灯笼和大灯笼的单价各是多少元
【答案】解:1÷=4(个)
112÷(4+12)
=112÷16
=7(元)
7÷=28(元)
答:小灯笼的单价是7元,大灯笼的单价是28元。
【解析】【分析】一个大灯笼相当于小灯笼的个数=1÷一个小灯笼是一个大灯笼单价的几分之几,所以小灯笼的单价=一个大灯笼和12个小灯笼一共的钱数÷(12+4),大灯笼的单价=小灯笼的单价÷乙个小灯笼是一个大灯笼单价的几分之几,据此代入数值作答即可。
23.一项工程,甲队单独做10天完成,乙队的工作效率是甲队的。如果甲、乙两队合做,几天可以完成这项工程的?
【答案】解:×=
÷(+)
=÷
=5(天)
答:5天可以完成这项工程的。
【解析】【分析】乙队的工作效率=甲队的工作效率×乙队的工作效率是甲队的几分之几,把这项工程看成单位“1”,那么完成这项工程的需要的天数=÷甲队和乙队的工作效率之和,据此代入数值作答即可。
24.(2023-2024六上·新田期末)果园里有苹果树120棵。桃树的棵树是苹果树的,还是梨树的,果园里有梨树多少棵?
【答案】解:桃:120× = 80(棵)
梨:80÷ =80× = 100(棵)
答:果园里有梨树100棵。
【解析】【分析】桃树的棵树=苹果树的棵数×;桃树的棵树是梨树的,由此可以推出,梨树的棵数=桃树的棵树÷。
25.(2023-2024六上·淮滨月考)十一假期期间,聪聪一家开车去鸡公山景区游玩,小时行驶了90千米,正好是全程的。
(1)聪聪从家到鸡公山景区有多少千米
(2)聪聪从家开车到鸡公山景区一共需要多少小时
【答案】(1)解:90÷=270(千米)
答:聪聪从家到鸡公山景区有270千米。
(2)解:270÷(90÷)
=270÷108
=2.5(小时)
答:聪聪从家开车到鸡公山景区一共需要2.5小时。
【解析】【分析】(1)已经行驶的路程÷已经行驶的路程占全程的分率=全程;
(2)已经行驶的路程÷时间=速度,全程÷(已经行驶的路程÷已经行驶的时间)=一共需要的时间。
26.(2023-2024六上·淮滨月考)实验小学足球社团有54人,是舞蹈社团人数的,比合唱社团的人数少,舞蹈社团和合唱社团各有多少人?
【答案】解:54÷=45(人)
54÷(1-)
=54÷
=63(人)
答:舞蹈社团有45人,合唱社团63人。
【解析】【分析】足球社团人数÷足球社团是舞蹈社团人数的分率=舞蹈社团人数;1-足球社团比合唱社团少的分率=足球社团占合唱社团的分率,足球社团人数÷足球社团占合唱社团的分率=合唱社团人数。
27.(2023-2024六上·阳春期中)修一条公路,甲队单独修要15天完成,乙队单独修要20天完成,甲乙两队一起修了6天后,甲队有事离开了,由乙队单独修完,乙队还需要多少天?
【答案】解:[1-(+)×6]÷
=[1-×6]÷
=÷
=6(天)
答:乙队还需6天。
【解析】【分析】剩下的乙队单独修完需要的天数=(1-甲、乙工作效率的和×工作时间) ÷乙的工作效率。
28.筑路队修一条10千米的公路.第一天修了全长的 ,第二天修了 千米,还有多少千米没有修?
【答案】解:10﹣10× ﹣
=10﹣2﹣1.5
=6.5(千米)
答:还有6.5千米没有修。
【解析】【分析】根据题意可知,把这条公路的全长看作单位“1”,先求出第一天修的长度,用总长度×第一天修的占全长的分率=第一天修的长度,然后用这条公路的全长-第一天修的长度-第二天修的长度=剩下没有修的长度,据此列式解答.
29.(2023-2024六上·天河期末)冬至是一年中白昼最短、黑夜最长的一天。这一天,某地的白昼时间是黑夜时间的 ,该地冬至的白昼时间是多少小时?
【答案】解:24÷(1+ )
=24÷
=14(小时)
14× =10(小时)
答:白昼时间是10小时。
【解析】【分析】该地冬至的白昼时间=冬至这一天黑夜的时间×占的分率;其中,冬至这一天黑夜时间=一天的时间÷(1+ )。
30.(2023-2024六上·岑巩期中)开学初, 阳光小学共有 84 名同学参加了少先队大队委的竞选活动。其中女生人数是男生人数的 , 参加竞选活动的男生、女生各有多少人?
【答案】解:84÷(1+)
=84÷
=48(人)
84-48=36(人)
答:参加竞选活动的男生有48人,女生36人。
【解析】【分析】参加竞选活动的男生人数=总人数÷(1+),女生人数=总人数-男生人数。
31.(2023-2024六上·播州期中)小军看一本故事书, 第一周看了全书的 , 第二周看了余下的 , 还剩 75 页没有读, 这本故事书有多少页
【答案】解:(1-)×
=×
=
75÷(1--)
=75÷
=180(页)
答:这本故事书有180页。
【解析】【分析】这本故事书的页数=还剩下的页数÷(1-第一周看的分率-第二周看的分率)。
32.(2023-2024六上·张湾期中)一辆大巴从A地出发,以80千米每时的速度行驶,6小时到达B地,如果大巴速度再快,几小时可到达B地?
【答案】解:80×6÷[80×(1)]
=480÷96
=5(小时)
答:5小时可到达B地。
【解析】【分析】大巴的速度×行驶的时间=总路程,大巴的速度×(1+)=大巴提速后的速度,总路程÷大巴提速后的速度=到达B地需要的时间。
33.(2023-2024六上·鄂城期中)迎宾大道铺沥青,工程队每天修千米,8天后,还剩下全长的,迎宾大道全长多少千米?
【答案】解:×8=18(千米)
18÷(1-)
=18÷
=20(千米)
答:迎宾大道全长20千米。
【解析】【分析】 迎宾大道全长=平均每天修的米数×已经修的天数÷(1-还剩下的分率)。
34.(2023-2024六上·桂林月考)书的人类进步的阶梯,天天小学举行“读书增智”的活动,活动期间,明明读一本名人传记,第一天读了全书的,第二天读了余下的,还剩60页没有读,这本名人传记共有多少页?
【答案】解:(1-)×+
=×+
=
60÷(1-)
=60÷
=240(页)
答:这本名人传记共有240页。
【解析】【分析】这本名人传记共有的页数=还剩下的页数÷(1-已经看的分率);其中,已经看的分率=第一天看的分率+第二天看的分率;第二天看的分率=(1-第一天看的分率)×。
35.(2023-2024六上·播州期中)某救援小队奉命为灾区运送救灾物资,救援小队已经行驶了全程的,如果再行驶15km,那么就行驶了全程的一半。救援小队的出发地距离灾区多少千米
【答案】解:5÷(-)
=5÷
=50(千米)
答:救援小队的出发地距离灾区50千米。
【解析】【分析】全程的一半是,救援小队的出发地距离灾区的路程=再行驶的5千米÷(-)。
36.(2023-2024六上·邢台期中)学校安排六年级学生做小红旗,六⑴班做了60面小红旗,比六⑵班少做了,你能算出六⑴班比六⑵班同学少做了多少面小红旗吗?
【答案】解:60÷(1-)
=60÷
=80(面)
80-60=20(面)
答:六⑴班比六⑵班同学少做了20面小红旗。
【解析】【分析】六(1)班比六(2)班同学少做小红旗的面数=六(2)班同学做小红旗的面数-六(1)班同学做小红旗的面数;其中,六(2)班同学做小红旗的面数=六(1)班同学做小红旗的面数÷(1-)。
37.(2023-2024六上·邢台期中)甲、乙两个修路队合修一条路,甲队已经修了40千米,乙队已经修了44千米,乙队修的比甲队修的多这条路的,这条路全长多少千米?
【答案】解:(44-40)÷
=4÷
=112(千米)
答:这条路全长112千米。
【解析】【分析】这条路的全长=(乙队修的长度-甲队修的长度)÷乙队修的比甲队多修的分率。
38.在某大坝截流时,用载重卡车将一堆石料运到围堰龙口,第一次运了这堆石料的少2万方,第二次运了剩下的多3万方,此时还剩下12万方未运,则这堆石料共有多少万方?
【答案】解:(12+3)÷(1-)
=15÷
=30(万方)
(30-2)÷(1-)
=28÷
=42(万方)
答:这堆石料共有42万方。
【解析】【分析】用逆推法:先把余下的质量看作单位“1”,假设第二天运来剩下的,则还剩下余下的1-=,还剩12+3=15万方,则余下15÷=30万方;进而把这堆石料看作单位“1”,第一次运了这堆石料的少2万方,然后用除法求出这堆石料共有多少万方。
39.(2023-2024六上·莲湖期末)某路段为了防止内涝,需要挖一条1200 米长的下水道,第一周挖了总长的 ,比第二周挖的长度短 ,第二周挖了多少米?
【答案】解:1200×÷(1-)
=180÷
=210(米)
答:第二周挖了210米。
【解析】【分析】第二周挖的米数=第一周挖的米数÷(1-短的分率),其中,第一周挖的米数=要挖下水道的总长×第一周挖的分率。
40.(2023-2024六上·平果期中)希望小学即将迎来10周华校庆,六⑴班准备召开校庆联欢会,小江和小南负资布置教室。小江单独挂彩条,需要12分钟:小南单独挂彩条,需要24分钟。
(1)如果两人合作挂彩条需要多长时间
(2)如果两人合作4分钟后,小南去摆桌椅,由小江单独挂剩下的彩条,还需要多长时问才能把彩条排好
【答案】(1)解:1÷(+)
=1÷
=8(分钟)
答:如果两人合作挂彩条需要8分钟。
(2)解:[1-(+)×4]÷
=[1-]÷
=÷
=6(分钟)
答:还需要6分钟时间才能把彩带排好。
【解析】【分析】(1)如果两人合作挂彩条需要的时间=1÷工作效率的和;
(2)把彩带排好,还需要的时间=(1-两人工作效率的和×4)÷小江的工作效率。
21世纪教育网(www.21cnjy.com)
六年级数学上册专项精练(知识梳理+典例精讲+专项精练)
1、倒数的意义:乘积是1的两个数互为倒数。
2、倒数具备两个条件:一是两个数;二是乘积是1。
3、互为倒数的两个数的特点。
(1)如果两个数都是分数,那么两个分数的分子和分母正好颠倒了位置;
(2)如果一个是整数,则另一个分数的分子是1,分母是这个整数。
4、求一个数的倒数的方法。
(1)求一个分数的倒数,把这个分数的分子、分母交换位置即可;
(2)求小数的倒数,先把小数化成分数,再求倒数;
(3)求非0整数的倒数,让这个整数作分母,分子是1。
5、注意事项:
(1)1的倒数是1,等于它本身;
(2)0没有倒数。
6、易错点:
(1)易错点在于混淆倒数定义。记住,乘积为1的两个数互为倒数,如5的倒数是 。计算时,常错将分子分母颠倒而不求其积为1,如误将 的倒数写为 的相反数。务必理解并准确应用倒数概念。
1、分数除以整数的计算方法。
(1)当一个分数被除以一个非零整数时,其结果等同于该分数乘以该整数的倒数。
在数学运算中,当遇到分子能够被某个整数整除的情况时,应采取以下步骤进行化简:将原分子除以该整数,并将所得的商作为新的分子,而分母则保持不变。这一操作确保了分数的等价性,同时简化了其表达形式。
2、一个数除以分数。
(1) 整数除以分数的计算方法:整数除以分数,用这个整数乘这个分数的倒数。
(2)分数除以分数的计算方法:分数除以分数,用被除数乘除数的倒数。
(3)分数除法的一般方法:一个数除以一个不等于0的数,等于乘这个数的倒数。
3、被除数与商的变化规律。
(1)除以大于 1 的数,商小于被除数:a÷b=c 当b>1时,c<a (a≠0);
(2)除以小于 1 的数,商大于被除数:a÷b=c 当b<1时,c>a (a≠0,b≠0);
(3)除以等于 1 的数,商等于被除数:a÷b=c 当b=1时,c=a。
4、易错点:分数除法时,易混淆除数与被除数位置,将分数除以整数误变为倒数相乘。同时,解题时易忽视找单位“1”,导致等量关系错误。此外,还需注意混合运算顺序,以及理解分数除法与乘法的互逆关系。
1、情况一:在进行同级运算时,应当严格遵循从左至右的顺序进行计算。
2、情况二:在进行数学运算时,若未涉及小括号,则需遵循既定的运算优先级规则,即先进行乘除运算,随后再执行加减运算。
3、情况三:在进行数学运算时,若表达式中包含小括号,则应首先计算小括号内的运算,待小括号内的运算完成后,再进行小括号外的运算。这是数学运算的基本规则之一,旨在确保运算的准确性和逻辑性。
4、易错点:混淆运算顺序,如先加减后乘除;忽视括号优先级,去括号时符号出错;错用运算律,如乘法分配律误用于除法;对分数意义理解不足,导致计算错误。需特别注意运算规则与分数性质,确保计算准确。
1、“已知一个数的几分之几是多少,求这个数”的方法:
已知量÷已知量占单位“1”的几分之几=单位“1”的量;
2、“已知比一个数多(或少)几分之几的数是多少,求这个数”的方法:
单位“1”的量×(1±几分之几)=已知量
单位“1”的量±单位“1”的量×几分之几=已知量
3、“已知两个量的和(差),其中一个量是另一个量的几分之几,求这两个量”的问题的解法:
有两个量都是未知的,先把谁看作单位“1”都可以,再用方程法求解:
(1)找出单位“1”,设未知量为x;
(2)找出题中的等量关系式;
(3)列出方程并解答;
(4)检验并写出答案。
4、工程问题。
(1)工作时间=工作总量÷工作效率
(2)利用抽象的“1”解决实际问题:
工程问题是分数问题的特例,工作总量与工作效率都不是具体的数,而是用抽象的分数来表示。一般地,工作总量用单位“1”来表示,工作效率则用完成总量所需时间的倒数来表示。
5、易错点:易错点在于混淆了乘除法的应用情境。例如,在涉及单价、数量、总价和工程的问题中,学生可能错误地将单价乘以数量视为总价,或反过来用总价除以数量得到单价,导致计算结果错误。此外,未准确理解题目中的比例关系也是常见错误。因此,审题需细致,理解题意后再选择正确算法,完成解题后,务必结合实际推理检验。
【典例精讲1】.“a是一个整数,它的倒数一定是。”这句话对吗?请说明理由。
【答案】解:这句话不对。如果a是0,0也是整数,但0没有倒数。
【解析】【分析】求一个数(0除外)的倒数=1÷这个数,因为0不能作除数,所以和这个数不能是0。
【典例精讲2】.(2023-2024-2024六上·万载月考)一根m 长的钢管重 10kg,这种钢管每米重多少千克?每千克钢管有多少米?
【答案】解:10÷=16(千克)
÷10=(米)
答:这种钢管每米重16千克,每千克钢管有米。
【解析】【分析】这种钢管每米重的质量=总质量÷这种钢管的长度;每千克钢管的长度=总长度÷总质量。
【典例精讲3】.(2023-2024-2024六上·五华月考)一个制药厂每天可以提炼t药材,现因业务需要,计划提炼t药材。则提炼这批药材需要多少天?
【答案】解: =7.5(天)
答:提炼这批药材需要7.5天。
【解析】【分析】提炼这批药材需要的天数=提炼药材的总质量÷平均每天提炼药材的质量。
【典例精讲4】.(2023-2024-2024六上·易门月考)一罐千克的奶粉,小峰最多可以喝几天,最少可以喝几天?
【答案】解:=7(天)
=3.5(天)
答:小峰最多可以喝7天,最少可以喝3.5天。
【解析】【分析】小峰最多可以喝的天数=一罐奶粉的质量÷小峰每天最少喝的质量,小峰最少可以喝的天数=一罐奶粉的质量÷小峰每天最多喝的质量,据此代入数值作答即可。
【典例精讲5】.(2023-2024-2024六上·期末)学校图书室里有故事书有390本,比科技书的本数多。学校图书室里有多少本科技书?
【答案】解:390÷(1+)
=390÷
=390×
=240(本)
答:学校图书室里有240本科技书。
【解析】【分析】将科技书的本数看作单位“1”,则故事书的本数是科技书的1+,求单位“1”用除法。科技书的本数=故事书的本数÷故事书的本数是科技书的几分之几。
【典例精讲6】.(2023-2024-2024六上·钱塘)美丽乡村建设时,某工程队修一条路,第二天修的长度是第一天的,两天一共修了600米,则第二天比第一天少修多少米?
【答案】解:600÷(1+ )
=600÷
=320 (米)
600-320=280 (米)
320-280=40 (米)
答:则第二天比第一天少修40米。
【解析】【分析】把第一天修的长度看成单位“1”,所以第一天修的长度=两天一共修的长度÷两天一共修了几分之几,第二天修的长度=两天一共修的长度-第一天修的长度,那么第二天比第一天少修的长度=第一天修的长度-第二天修的长度,据此代入数值作答即可。
【典例精讲7】.(2023-2024-2024六上·金乡县期中)一段路长 3600米,甲工程队单独修需要30天完成,乙工程队单独修需要45天,两队合修几天可修这条路的三分之二?
【答案】解:3600×=2400(米)
3600÷30=120(米)
3600÷45=80(米)
2400÷(120+80)
=2400÷200
=12(天)
答:两队合修12天可修这条路的三分之二。
【解析】【分析】这条路的三分之二的长度=这条路的长度×,甲工程队每天修的长度=这条路的长度÷甲工程队单独修完需要的天数,乙工程队每天修的长度=这条路的长度÷乙工程队单独修完需要的天数,那么两队合修完成这条路的三分之二需要的天数=这条路的三分之二的长度÷两工程队每天一共修的长度,据此代入数值作答即可。
应用题。
一本故事书,小瑞第一天看了第二天看了刚好看到第60页,这本书有多少页
2.(2023-2024六上·英山期末)新洲小学购买一批图书,其中科技书有280本,正好是这批图书的,这批图书一共有多少本?
3.(2023-2024六上·凉州期末)一杯250毫升的鲜牛奶含有克的钙质,占一个成年人一天所需钙质的。一个成年人一天需要多少钙质?
4.(2023-2024六上·余杭月考)某工程队修一条长500米的公路,5天后,未修的公路长度是已修公路长度的。工程队已经修了多少米?
5.(2023-2024六上·阳春期中)六年级男生比女生多60人,女生人数是男生人数的,六年级男、女生各有多少人?
6.(2023-2024六上·阳春期中)一辆汽车以每小时45千米的速度从甲地到乙地,3小时行了全程的,这辆汽车还要行多少千米才能到达乙地?
7.(2023-2024六上·斗门期中)小东看一本科技书,已经看了210页,占全书页数的 。这本科技书有多少页?(先用线段图表示题中数量关系,再解答)。
(2023-2024六上·龙岗期中)某工厂九月份用水30吨,九月份比十月份多用水,十月份用多少吨?
9.狮子奔跑时的最高速度可以达到60千米/时,比猎豹奔跑时的最高速度慢。猎豹奔跑时的最高速度是多少?
10.(2023-2024六上·永福期中) 小宇的体重是42千克,小宇的体重比爸爸的体重轻,爸爸的体重是多少千克?
11.(2023-2024六上·红安期中)一项工程,甲单独做20天完成,乙单独做用30天完成。甲、乙两队合修3天后,雨下的由乙队做,需要多少天才能完成?
12.(2023-2024六上·张湾期中)六年级同学为学校图书馆整理图书,他们已经整理了300本,还剩没有整理。需要整理的图书一共有多少本?
13.(2023-2024六上·张湾期中)服装厂接到一批订单,第一车间单独做需要10天完成,第二车间单独做3天完成了,如果两个车间同时做这批订单,多少天可以完成这批订单?
14.(2023-2024六上·监利期中)一辆货车从甲地开往乙地,已行全程的,距中点还有25千米,甲乙两地相距多少千米?
15.(2023-2024六上·鄂城期中)某工厂全部改用节能LED灯具后,现在每月照明用电量是185千瓦时,比原来每月节约,原来每月用电量是多少千瓦时?
16.(2023-2024六上·涟源期中)李老师从新化开车去长沙,行了全程的后,还剩下90km没有行,从新化到长沙共有多少千米?
17.(2023-2024六上·新田期中) 一项工程,甲单独做8天可以完成,乙单独做6天可以完成。
(1)甲乙合作一起完成,需要多少天?
(2)如果由乙先做3天,剩下的由甲来做,还需要多少天能完成这项工程?
(2023-2024六上·慈利期中)国庆节布置教室,六⑴班一共需要做320朵黄花,其中黄花的朵数是红花朵数的,红花比黄花多多少朵?
19.张师傅带了一些钱去购买办公桌椅。这些钱如果全部用来购买桌子,可以买20张;如果全部用来购买椅子,可以买30把。这些钱可以买多少套办公桌椅?(一张桌子和一把椅子是1套)
20.(2023-2024六上·黔江期末) 水果批发市场新进一批水果,运来苹果3吨,比运来橘子的少0.2吨,运来橘子多少吨?
21.一年好景君须记,最是橙黄橘绿时”,果园里橘子大丰收了!今年王奶奶还尝试了“直播带货”,销量大增,一共卖出了3500千克,其中通过直播卖出的橘子数量是线下的。线上直播卖出了多少千克
22.为迎接新年,实验小学六(3)班布置教室,买了一个大灯笼和12个小灯笼,一共花费112元.已知一个小灯笼是一个大灯笼单价的。小灯笼和大灯笼的单价各是多少元
23.一项工程,甲队单独做10天完成,乙队的工作效率是甲队的。如果甲、乙两队合做,几天可以完成这项工程的?
24.(2023-2024六上·新田期末)果园里有苹果树120棵。桃树的棵树是苹果树的,还是梨树的,果园里有梨树多少棵?
25.(2023-2024六上·淮滨月考)十一假期期间,聪聪一家开车去鸡公山景区游玩,小时行驶了90千米,正好是全程的。
(1)聪聪从家到鸡公山景区有多少千米
(2)聪聪从家开车到鸡公山景区一共需要多少小时
26.(2023-2024六上·淮滨月考)实验小学足球社团有54人,是舞蹈社团人数的,比合唱社团的人数少,舞蹈社团和合唱社团各有多少人?
27.(2023-2024六上·阳春期中)修一条公路,甲队单独修要15天完成,乙队单独修要20天完成,甲乙两队一起修了6天后,甲队有事离开了,由乙队单独修完,乙队还需要多少天?
28.筑路队修一条10千米的公路.第一天修了全长的 ,第二天修了 千米,还有多少千米没有修?
29.(2023-2024六上·天河期末)冬至是一年中白昼最短、黑夜最长的一天。这一天,某地的白昼时间是黑夜时间的 ,该地冬至的白昼时间是多少小时?
30.(2023-2024六上·岑巩期中)开学初, 阳光小学共有 84 名同学参加了少先队大队委的竞选活动。其中女生人数是男生人数的 , 参加竞选活动的男生、女生各有多少人?
31.(2023-2024六上·播州期中)小军看一本故事书, 第一周看了全书的 , 第二周看了余下的 , 还剩 75 页没有读, 这本故事书有多少页
32.(2023-2024六上·张湾期中)一辆大巴从A地出发,以80千米每时的速度行驶,6小时到达B地,如果大巴速度再快,几小时可到达B地?
33.(2023-2024六上·鄂城期中)迎宾大道铺沥青,工程队每天修千米,8天后,还剩下全长的,迎宾大道全长多少千米?
34.(2023-2024六上·桂林月考)书的人类进步的阶梯,天天小学举行“读书增智”的活动,活动期间,明明读一本名人传记,第一天读了全书的,第二天读了余下的,还剩60页没有读,这本名人传记共有多少页?
35.(2023-2024六上·播州期中)某救援小队奉命为灾区运送救灾物资,救援小队已经行驶了全程的,如果再行驶15km,那么就行驶了全程的一半。救援小队的出发地距离灾区多少千米
36.(2023-2024六上·邢台期中)学校安排六年级学生做小红旗,六⑴班做了60面小红旗,比六⑵班少做了,你能算出六⑴班比六⑵班同学少做了多少面小红旗吗?
37.(2023-2024六上·邢台期中)甲、乙两个修路队合修一条路,甲队已经修了40千米,乙队已经修了44千米,乙队修的比甲队修的多这条路的,这条路全长多少千米?
38.在某大坝截流时,用载重卡车将一堆石料运到围堰龙口,第一次运了这堆石料的少2万方,第二次运了剩下的多3万方,此时还剩下12万方未运,则这堆石料共有多少万方?
39.(2023-2024六上·莲湖期末)某路段为了防止内涝,需要挖一条1200 米长的下水道,第一周挖了总长的 ,比第二周挖的长度短 ,第二周挖了多少米?
40.(2023-2024六上·平果期中)希望小学即将迎来10周华校庆,六⑴班准备召开校庆联欢会,小江和小南负资布置教室。小江单独挂彩条,需要12分钟:小南单独挂彩条,需要24分钟。
(1)如果两人合作挂彩条需要多长时间
(2)如果两人合作4分钟后,小南去摆桌椅,由小江单独挂剩下的彩条,还需要多长时问才能把彩条排好
21世纪教育网(www.21cnjy.com)
第三单元 分数除法 单元复习讲义(讲义)
六年级数学上册专项精练(知识梳理+典例精讲+专项精练)
1、倒数的意义:乘积是1的两个数互为倒数。
2、倒数具备两个条件:一是两个数;二是乘积是1。
3、互为倒数的两个数的特点。
(1)如果两个数都是分数,那么两个分数的分子和分母正好颠倒了位置;
(2)如果一个是整数,则另一个分数的分子是1,分母是这个整数。
4、求一个数的倒数的方法。
(1)求一个分数的倒数,把这个分数的分子、分母交换位置即可;
(2)求小数的倒数,先把小数化成分数,再求倒数;
(3)求非0整数的倒数,让这个整数作分母,分子是1。
5、注意事项:
(1)1的倒数是1,等于它本身;
(2)0没有倒数。
6、易错点:
(1)易错点在于混淆倒数定义。记住,乘积为1的两个数互为倒数,如5的倒数是 。计算时,常错将分子分母颠倒而不求其积为1,如误将 的倒数写为 的相反数。务必理解并准确应用倒数概念。
1、分数除以整数的计算方法。
(1)当一个分数被除以一个非零整数时,其结果等同于该分数乘以该整数的倒数。
在数学运算中,当遇到分子能够被某个整数整除的情况时,应采取以下步骤进行化简:将原分子除以该整数,并将所得的商作为新的分子,而分母则保持不变。这一操作确保了分数的等价性,同时简化了其表达形式。
2、一个数除以分数。
(1) 整数除以分数的计算方法:整数除以分数,用这个整数乘这个分数的倒数。
(2)分数除以分数的计算方法:分数除以分数,用被除数乘除数的倒数。
(3)分数除法的一般方法:一个数除以一个不等于0的数,等于乘这个数的倒数。
3、被除数与商的变化规律。
(1)除以大于 1 的数,商小于被除数:a÷b=c 当b>1时,c<a (a≠0);
(2)除以小于 1 的数,商大于被除数:a÷b=c 当b<1时,c>a (a≠0,b≠0);
(3)除以等于 1 的数,商等于被除数:a÷b=c 当b=1时,c=a。
4、易错点:分数除法时,易混淆除数与被除数位置,将分数除以整数误变为倒数相乘。同时,解题时易忽视找单位“1”,导致等量关系错误。此外,还需注意混合运算顺序,以及理解分数除法与乘法的互逆关系。
1、情况一:在进行同级运算时,应当严格遵循从左至右的顺序进行计算。
2、情况二:在进行数学运算时,若未涉及小括号,则需遵循既定的运算优先级规则,即先进行乘除运算,随后再执行加减运算。
3、情况三:在进行数学运算时,若表达式中包含小括号,则应首先计算小括号内的运算,待小括号内的运算完成后,再进行小括号外的运算。这是数学运算的基本规则之一,旨在确保运算的准确性和逻辑性。
4、易错点:混淆运算顺序,如先加减后乘除;忽视括号优先级,去括号时符号出错;错用运算律,如乘法分配律误用于除法;对分数意义理解不足,导致计算错误。需特别注意运算规则与分数性质,确保计算准确。
1、“已知一个数的几分之几是多少,求这个数”的方法:
已知量÷已知量占单位“1”的几分之几=单位“1”的量;
2、“已知比一个数多(或少)几分之几的数是多少,求这个数”的方法:
单位“1”的量×(1±几分之几)=已知量
单位“1”的量±单位“1”的量×几分之几=已知量
3、“已知两个量的和(差),其中一个量是另一个量的几分之几,求这两个量”的问题的解法:
有两个量都是未知的,先把谁看作单位“1”都可以,再用方程法求解:
(1)找出单位“1”,设未知量为x;
(2)找出题中的等量关系式;
(3)列出方程并解答;
(4)检验并写出答案。
4、工程问题。
(1)工作时间=工作总量÷工作效率
(2)利用抽象的“1”解决实际问题:
工程问题是分数问题的特例,工作总量与工作效率都不是具体的数,而是用抽象的分数来表示。一般地,工作总量用单位“1”来表示,工作效率则用完成总量所需时间的倒数来表示。
5、易错点:易错点在于混淆了乘除法的应用情境。例如,在涉及单价、数量、总价和工程的问题中,学生可能错误地将单价乘以数量视为总价,或反过来用总价除以数量得到单价,导致计算结果错误。此外,未准确理解题目中的比例关系也是常见错误。因此,审题需细致,理解题意后再选择正确算法,完成解题后,务必结合实际推理检验。
【典例精讲1】.“a是一个整数,它的倒数一定是。”这句话对吗?请说明理由。
【答案】解:这句话不对。如果a是0,0也是整数,但0没有倒数。
【解析】【分析】求一个数(0除外)的倒数=1÷这个数,因为0不能作除数,所以和这个数不能是0。
【典例精讲2】.(2023-2024-2024-2024六上·万载月考)一根m 长的钢管重 10kg,这种钢管每米重多少千克?每千克钢管有多少米?
【答案】解:10÷=16(千克)
÷10=(米)
答:这种钢管每米重16千克,每千克钢管有米。
【解析】【分析】这种钢管每米重的质量=总质量÷这种钢管的长度;每千克钢管的长度=总长度÷总质量。
【典例精讲3】.(2023-2024-2024-2024六上·五华月考)一个制药厂每天可以提炼t药材,现因业务需要,计划提炼t药材。则提炼这批药材需要多少天?
【答案】解: =7.5(天)
答:提炼这批药材需要7.5天。
【解析】【分析】提炼这批药材需要的天数=提炼药材的总质量÷平均每天提炼药材的质量。
【典例精讲4】.(2023-2024-2024-2024六上·易门月考)一罐千克的奶粉,小峰最多可以喝几天,最少可以喝几天?
【答案】解:=7(天)
=3.5(天)
答:小峰最多可以喝7天,最少可以喝3.5天。
【解析】【分析】小峰最多可以喝的天数=一罐奶粉的质量÷小峰每天最少喝的质量,小峰最少可以喝的天数=一罐奶粉的质量÷小峰每天最多喝的质量,据此代入数值作答即可。
【典例精讲5】.(2023-2024-2024-2024六上·期末)学校图书室里有故事书有390本,比科技书的本数多。学校图书室里有多少本科技书?
【答案】解:390÷(1+)
=390÷
=390×
=240(本)
答:学校图书室里有240本科技书。
【解析】【分析】将科技书的本数看作单位“1”,则故事书的本数是科技书的1+,求单位“1”用除法。科技书的本数=故事书的本数÷故事书的本数是科技书的几分之几。
【典例精讲6】.(2023-2024-2024-2024六上·钱塘)美丽乡村建设时,某工程队修一条路,第二天修的长度是第一天的,两天一共修了600米,则第二天比第一天少修多少米?
【答案】解:600÷(1+ )
=600÷
=320 (米)
600-320=280 (米)
320-280=40 (米)
答:则第二天比第一天少修40米。
【解析】【分析】把第一天修的长度看成单位“1”,所以第一天修的长度=两天一共修的长度÷两天一共修了几分之几,第二天修的长度=两天一共修的长度-第一天修的长度,那么第二天比第一天少修的长度=第一天修的长度-第二天修的长度,据此代入数值作答即可。
【典例精讲7】.(2023-2024-2024-2024六上·金乡县期中)一段路长 3600米,甲工程队单独修需要30天完成,乙工程队单独修需要45天,两队合修几天可修这条路的三分之二?
【答案】解:3600×=2400(米)
3600÷30=120(米)
3600÷45=80(米)
2400÷(120+80)
=2400÷200
=12(天)
答:两队合修12天可修这条路的三分之二。
【解析】【分析】这条路的三分之二的长度=这条路的长度×,甲工程队每天修的长度=这条路的长度÷甲工程队单独修完需要的天数,乙工程队每天修的长度=这条路的长度÷乙工程队单独修完需要的天数,那么两队合修完成这条路的三分之二需要的天数=这条路的三分之二的长度÷两工程队每天一共修的长度,据此代入数值作答即可。
应用题。
1.一本故事书,小瑞第一天看了第二天看了刚好看到第60页,这本书有多少页
【答案】解:60÷(+)
=60÷
=175(页)
答:这本书有175页。
【解析】【分析】这本书的总页数=已经看的页数÷(第一天看的分率+第二天看的分率)。
2.(2023-2024六上·英山期末)新洲小学购买一批图书,其中科技书有280本,正好是这批图书的,这批图书一共有多少本?
【答案】解:280÷=2450(本)
答:这批图书一共有2450本。
【解析】【分析】根据题意,把这批图书的总本数看作单位“1”,求单位“1”用除法计算,科技书的本数÷科技书占图书的=图书的总本数,据此列式解答。
3.(2023-2024六上·凉州期末)一杯250毫升的鲜牛奶含有克的钙质,占一个成年人一天所需钙质的。一个成年人一天需要多少钙质?
【答案】解:÷ =(千克)
答:一个成年人一天需要 克钙质。
【解析】【分析】一个成年人一天需要钙质的质量=一杯250毫升的鲜牛奶中钙质的质量÷一个成年人一天所需钙质的分率。
4.(2023-2024六上·余杭月考)某工程队修一条长500米的公路,5天后,未修的公路长度是已修公路长度的。工程队已经修了多少米?
【答案】解:500÷(1+)
=500÷
=312.5(米)
答:工程队已经修了312.5米。
【解析】【分析】工程队已经修的米数=这条公路的总长÷(1+)。
5.(2023-2024六上·阳春期中)六年级男生比女生多60人,女生人数是男生人数的,六年级男、女生各有多少人?
【答案】解:60÷(1- )
=60÷
=600(人)
600+60=660(人)
答:六年级男生660人,女生600人。
【解析】【分析】六年级女生人数=六年级男生比女生多的人数÷(1-) ,六年级男生人数=六年级女生人数+多的60人。
6.(2023-2024六上·阳春期中)一辆汽车以每小时45千米的速度从甲地到乙地,3小时行了全程的,这辆汽车还要行多少千米才能到达乙地?
【答案】解:45×3÷ -45×3
=189-135
=54(千米)
答:这辆汽车还要行54千米才能到达乙地。
【解析】【分析】到达乙地这辆汽车还要行驶的路程=这辆汽车的速度×行驶的时间÷已经行驶的路程- 这辆汽车的速度×行驶的时间。
7.(2023-2024六上·斗门期中)小东看一本科技书,已经看了210页,占全书页数的 。这本科技书有多少页?(先用线段图表示题中数量关系,再解答)。
【答案】解:
210÷ =490(页)
答:这本科技书有490页。
【解析】【分析】这本科技书的页数=已经看的页数÷所占的百分率。
8.(2023-2024六上·龙岗期中)某工厂九月份用水30吨,九月份比十月份多用水,十月份用多少吨?
【答案】解:30÷(1+ )
=30÷
=25(吨)
答:十月份用水25吨。
【解析】【分析】十月份用水的吨数=九月份用水的吨数÷(1+多的分率)。
9.狮子奔跑时的最高速度可以达到60千米/时,比猎豹奔跑时的最高速度慢。猎豹奔跑时的最高速度是多少?
【答案】解:60÷(1-)
=60÷
=110(千米/时)
答:猎豹奔跑时的最高速度是110千米/时。
【解析】【分析】猎豹奔跑时的最高速度=狮子奔跑时的最高速度÷(1-慢的分率)。
10.(2023-2024六上·永福期中) 小宇的体重是42千克,小宇的体重比爸爸的体重轻,爸爸的体重是多少千克?
【答案】解:42÷(1-)
=42÷
=70(千克)
答:爸爸的体重是70千克。
【解析】【分析】爸爸的体重=小宇的体重÷(1-轻的分率)。
11.(2023-2024六上·红安期中)一项工程,甲单独做20天完成,乙单独做用30天完成。甲、乙两队合修3天后,雨下的由乙队做,需要多少天才能完成?
【答案】解:
=
=
=
=22.5(天)
答:需要22.5天才能完成
【解析】【分析】根据题目可知,甲的工作效率是,乙的工作效率是, 把这项工程看作单位“1”,用单位“1”减去甲、乙两队合作3天的工作量,得出剩下的工作总量,剩下的工作总量除以乙的工作效率即可求出需要的时间。
12.(2023-2024六上·张湾期中)六年级同学为学校图书馆整理图书,他们已经整理了300本,还剩没有整理。需要整理的图书一共有多少本?
【答案】解:300÷(1)
=300
=750(本)
答:需要整理的图书一共有750本。
【解析】【分析】已经整理的本数÷已经整理的本数占 需要整理的图书的分率= 需要整理的图书的本数。
13.(2023-2024六上·张湾期中)服装厂接到一批订单,第一车间单独做需要10天完成,第二车间单独做3天完成了,如果两个车间同时做这批订单,多少天可以完成这批订单?
【答案】解:1÷()
=1÷(+)
=1
=6(天)
答:6天可以完成。
【解析】【分析】工作总量1÷第一车间单独做需要的时间=第一车间的工作效率;第二车间单独做3天完成的工作效率÷3=第二车间的工作效率;单位1÷两个车间的工作效率之和=完成这批订单需要的时间。
14.(2023-2024六上·监利期中)一辆货车从甲地开往乙地,已行全程的,距中点还有25千米,甲乙两地相距多少千米?
【答案】解:25÷()
=25÷
=250(千米)
答:甲、乙两地相距250千米。
【解析】【分析】中点就是全程的,用减去求出距离中点的分率,根据分数除法的意义,用距离中点的长度除以距离中点的分率即可求出两地的距离。
15.(2023-2024六上·鄂城期中)某工厂全部改用节能LED灯具后,现在每月照明用电量是185千瓦时,比原来每月节约,原来每月用电量是多少千瓦时?
【答案】解:185÷(1-)
=185÷
=259(千瓦时)
答:原来每月用电量是259千瓦时。
【解析】【分析】原来每月用电量=现在每月用电量÷(1-节约的分率)。
16.(2023-2024六上·涟源期中)李老师从新化开车去长沙,行了全程的后,还剩下90km没有行,从新化到长沙共有多少千米?
【答案】解:90÷(1﹣)
=90÷
=225(千米)
答:从新化到长沙共有225千米。
【解析】【分析】90千米÷90千米对应全程的分率=全程。
17.(2023-2024六上·新田期中) 一项工程,甲单独做8天可以完成,乙单独做6天可以完成。
(1)甲乙合作一起完成,需要多少天?
(2)如果由乙先做3天,剩下的由甲来做,还需要多少天能完成这项工程?
【答案】(1)解:1÷8=,1÷6=
1÷(+)
=1÷
=(天)
答:需要天。
(2)解:(1-×3)÷
=×8
=4(天)
答:还需要4天能完成这项工程。
【解析】【分析】(1)把这项工程看成单位“1”,那么需要的天数=1÷甲、乙两人每天一共完成几分之几;
(2)乙先做3天,剩下几分之几=1-乙每天完成几分之几×3,那么还要的天数=剩下几分之几÷甲每天完成几分之几,据此代入数值作答即可。
18.(2023-2024六上·慈利期中)国庆节布置教室,六⑴班一共需要做320朵黄花,其中黄花的朵数是红花朵数的,红花比黄花多多少朵?
【答案】解:320÷-320
=400-320
=80(朵)
答:红花比黄花多80朵。
【解析】【分析】 黄花的朵数 ÷ 黄花的朵数占红花朵数的分率=红花朵数,红花朵数-黄花的朵数=红花比黄花多的朵数。
19.张师傅带了一些钱去购买办公桌椅。这些钱如果全部用来购买桌子,可以买20张;如果全部用来购买椅子,可以买30把。这些钱可以买多少套办公桌椅?(一张桌子和一把椅子是1套)
【答案】解:1÷(+)
=1÷
=12(套)
答:这些钱可以买12套办公桌椅。
【解析】【分析】把总钱数看作单位“1”,那么一张桌子的钱数就占总钱数的,一把椅子的钱数就占总钱数的;一套桌椅的钱数就占总钱数的(+),用单位“1”除以一套桌椅的分率即可解答。
20.(2023-2024六上·黔江期末) 水果批发市场新进一批水果,运来苹果3吨,比运来橘子的少0.2吨,运来橘子多少吨?
【答案】解:(3+0.2)÷
=3.2÷
=3.2×
=3.6(吨)
答:运来橘子3.6吨。
【解析】【分析】苹果比运来橘子的少0.2吨,说明橘子的是(3+0.2)吨,已知一个数的几分之几是多少,求这个数,用乘法。
21.一年好景君须记,最是橙黄橘绿时”,果园里橘子大丰收了!今年王奶奶还尝试了“直播带货”,销量大增,一共卖出了3500千克,其中通过直播卖出的橘子数量是线下的。线上直播卖出了多少千克
【答案】解:3500÷(1+)×
=3500÷×
=2000×
=1500(千克)
答:线上直播卖出了1500千克。
【解析】【分析】线上直播卖出的质量=卖出的总质量÷(1+线上直播占的分率)×线上直播占的分率。
22.为迎接新年,实验小学六(3)班布置教室,买了一个大灯笼和12个小灯笼,一共花费112元.已知一个小灯笼是一个大灯笼单价的。小灯笼和大灯笼的单价各是多少元
【答案】解:1÷=4(个)
112÷(4+12)
=112÷16
=7(元)
7÷=28(元)
答:小灯笼的单价是7元,大灯笼的单价是28元。
【解析】【分析】一个大灯笼相当于小灯笼的个数=1÷一个小灯笼是一个大灯笼单价的几分之几,所以小灯笼的单价=一个大灯笼和12个小灯笼一共的钱数÷(12+4),大灯笼的单价=小灯笼的单价÷乙个小灯笼是一个大灯笼单价的几分之几,据此代入数值作答即可。
23.一项工程,甲队单独做10天完成,乙队的工作效率是甲队的。如果甲、乙两队合做,几天可以完成这项工程的?
【答案】解:×=
÷(+)
=÷
=5(天)
答:5天可以完成这项工程的。
【解析】【分析】乙队的工作效率=甲队的工作效率×乙队的工作效率是甲队的几分之几,把这项工程看成单位“1”,那么完成这项工程的需要的天数=÷甲队和乙队的工作效率之和,据此代入数值作答即可。
24.(2023-2024六上·新田期末)果园里有苹果树120棵。桃树的棵树是苹果树的,还是梨树的,果园里有梨树多少棵?
【答案】解:桃:120× = 80(棵)
梨:80÷ =80× = 100(棵)
答:果园里有梨树100棵。
【解析】【分析】桃树的棵树=苹果树的棵数×;桃树的棵树是梨树的,由此可以推出,梨树的棵数=桃树的棵树÷。
25.(2023-2024六上·淮滨月考)十一假期期间,聪聪一家开车去鸡公山景区游玩,小时行驶了90千米,正好是全程的。
(1)聪聪从家到鸡公山景区有多少千米
(2)聪聪从家开车到鸡公山景区一共需要多少小时
【答案】(1)解:90÷=270(千米)
答:聪聪从家到鸡公山景区有270千米。
(2)解:270÷(90÷)
=270÷108
=2.5(小时)
答:聪聪从家开车到鸡公山景区一共需要2.5小时。
【解析】【分析】(1)已经行驶的路程÷已经行驶的路程占全程的分率=全程;
(2)已经行驶的路程÷时间=速度,全程÷(已经行驶的路程÷已经行驶的时间)=一共需要的时间。
26.(2023-2024六上·淮滨月考)实验小学足球社团有54人,是舞蹈社团人数的,比合唱社团的人数少,舞蹈社团和合唱社团各有多少人?
【答案】解:54÷=45(人)
54÷(1-)
=54÷
=63(人)
答:舞蹈社团有45人,合唱社团63人。
【解析】【分析】足球社团人数÷足球社团是舞蹈社团人数的分率=舞蹈社团人数;1-足球社团比合唱社团少的分率=足球社团占合唱社团的分率,足球社团人数÷足球社团占合唱社团的分率=合唱社团人数。
27.(2023-2024六上·阳春期中)修一条公路,甲队单独修要15天完成,乙队单独修要20天完成,甲乙两队一起修了6天后,甲队有事离开了,由乙队单独修完,乙队还需要多少天?
【答案】解:[1-(+)×6]÷
=[1-×6]÷
=÷
=6(天)
答:乙队还需6天。
【解析】【分析】剩下的乙队单独修完需要的天数=(1-甲、乙工作效率的和×工作时间) ÷乙的工作效率。
28.筑路队修一条10千米的公路.第一天修了全长的 ,第二天修了 千米,还有多少千米没有修?
【答案】解:10﹣10× ﹣
=10﹣2﹣1.5
=6.5(千米)
答:还有6.5千米没有修。
【解析】【分析】根据题意可知,把这条公路的全长看作单位“1”,先求出第一天修的长度,用总长度×第一天修的占全长的分率=第一天修的长度,然后用这条公路的全长-第一天修的长度-第二天修的长度=剩下没有修的长度,据此列式解答.
29.(2023-2024六上·天河期末)冬至是一年中白昼最短、黑夜最长的一天。这一天,某地的白昼时间是黑夜时间的 ,该地冬至的白昼时间是多少小时?
【答案】解:24÷(1+ )
=24÷
=14(小时)
14× =10(小时)
答:白昼时间是10小时。
【解析】【分析】该地冬至的白昼时间=冬至这一天黑夜的时间×占的分率;其中,冬至这一天黑夜时间=一天的时间÷(1+ )。
30.(2023-2024六上·岑巩期中)开学初, 阳光小学共有 84 名同学参加了少先队大队委的竞选活动。其中女生人数是男生人数的 , 参加竞选活动的男生、女生各有多少人?
【答案】解:84÷(1+)
=84÷
=48(人)
84-48=36(人)
答:参加竞选活动的男生有48人,女生36人。
【解析】【分析】参加竞选活动的男生人数=总人数÷(1+),女生人数=总人数-男生人数。
31.(2023-2024六上·播州期中)小军看一本故事书, 第一周看了全书的 , 第二周看了余下的 , 还剩 75 页没有读, 这本故事书有多少页
【答案】解:(1-)×
=×
=
75÷(1--)
=75÷
=180(页)
答:这本故事书有180页。
【解析】【分析】这本故事书的页数=还剩下的页数÷(1-第一周看的分率-第二周看的分率)。
32.(2023-2024六上·张湾期中)一辆大巴从A地出发,以80千米每时的速度行驶,6小时到达B地,如果大巴速度再快,几小时可到达B地?
【答案】解:80×6÷[80×(1)]
=480÷96
=5(小时)
答:5小时可到达B地。
【解析】【分析】大巴的速度×行驶的时间=总路程,大巴的速度×(1+)=大巴提速后的速度,总路程÷大巴提速后的速度=到达B地需要的时间。
33.(2023-2024六上·鄂城期中)迎宾大道铺沥青,工程队每天修千米,8天后,还剩下全长的,迎宾大道全长多少千米?
【答案】解:×8=18(千米)
18÷(1-)
=18÷
=20(千米)
答:迎宾大道全长20千米。
【解析】【分析】 迎宾大道全长=平均每天修的米数×已经修的天数÷(1-还剩下的分率)。
34.(2023-2024六上·桂林月考)书的人类进步的阶梯,天天小学举行“读书增智”的活动,活动期间,明明读一本名人传记,第一天读了全书的,第二天读了余下的,还剩60页没有读,这本名人传记共有多少页?
【答案】解:(1-)×+
=×+
=
60÷(1-)
=60÷
=240(页)
答:这本名人传记共有240页。
【解析】【分析】这本名人传记共有的页数=还剩下的页数÷(1-已经看的分率);其中,已经看的分率=第一天看的分率+第二天看的分率;第二天看的分率=(1-第一天看的分率)×。
35.(2023-2024六上·播州期中)某救援小队奉命为灾区运送救灾物资,救援小队已经行驶了全程的,如果再行驶15km,那么就行驶了全程的一半。救援小队的出发地距离灾区多少千米
【答案】解:5÷(-)
=5÷
=50(千米)
答:救援小队的出发地距离灾区50千米。
【解析】【分析】全程的一半是,救援小队的出发地距离灾区的路程=再行驶的5千米÷(-)。
36.(2023-2024六上·邢台期中)学校安排六年级学生做小红旗,六⑴班做了60面小红旗,比六⑵班少做了,你能算出六⑴班比六⑵班同学少做了多少面小红旗吗?
【答案】解:60÷(1-)
=60÷
=80(面)
80-60=20(面)
答:六⑴班比六⑵班同学少做了20面小红旗。
【解析】【分析】六(1)班比六(2)班同学少做小红旗的面数=六(2)班同学做小红旗的面数-六(1)班同学做小红旗的面数;其中,六(2)班同学做小红旗的面数=六(1)班同学做小红旗的面数÷(1-)。
37.(2023-2024六上·邢台期中)甲、乙两个修路队合修一条路,甲队已经修了40千米,乙队已经修了44千米,乙队修的比甲队修的多这条路的,这条路全长多少千米?
【答案】解:(44-40)÷
=4÷
=112(千米)
答:这条路全长112千米。
【解析】【分析】这条路的全长=(乙队修的长度-甲队修的长度)÷乙队修的比甲队多修的分率。
38.在某大坝截流时,用载重卡车将一堆石料运到围堰龙口,第一次运了这堆石料的少2万方,第二次运了剩下的多3万方,此时还剩下12万方未运,则这堆石料共有多少万方?
【答案】解:(12+3)÷(1-)
=15÷
=30(万方)
(30-2)÷(1-)
=28÷
=42(万方)
答:这堆石料共有42万方。
【解析】【分析】用逆推法:先把余下的质量看作单位“1”,假设第二天运来剩下的,则还剩下余下的1-=,还剩12+3=15万方,则余下15÷=30万方;进而把这堆石料看作单位“1”,第一次运了这堆石料的少2万方,然后用除法求出这堆石料共有多少万方。
39.(2023-2024六上·莲湖期末)某路段为了防止内涝,需要挖一条1200 米长的下水道,第一周挖了总长的 ,比第二周挖的长度短 ,第二周挖了多少米?
【答案】解:1200×÷(1-)
=180÷
=210(米)
答:第二周挖了210米。
【解析】【分析】第二周挖的米数=第一周挖的米数÷(1-短的分率),其中,第一周挖的米数=要挖下水道的总长×第一周挖的分率。
40.(2023-2024六上·平果期中)希望小学即将迎来10周华校庆,六⑴班准备召开校庆联欢会,小江和小南负资布置教室。小江单独挂彩条,需要12分钟:小南单独挂彩条,需要24分钟。
(1)如果两人合作挂彩条需要多长时间
(2)如果两人合作4分钟后,小南去摆桌椅,由小江单独挂剩下的彩条,还需要多长时问才能把彩条排好
【答案】(1)解:1÷(+)
=1÷
=8(分钟)
答:如果两人合作挂彩条需要8分钟。
(2)解:[1-(+)×4]÷
=[1-]÷
=÷
=6(分钟)
答:还需要6分钟时间才能把彩带排好。
【解析】【分析】(1)如果两人合作挂彩条需要的时间=1÷工作效率的和;
(2)把彩带排好,还需要的时间=(1-两人工作效率的和×4)÷小江的工作效率。
21世纪教育网(www.21cnjy.com)
