第四章 一次函数—八年级上册数学北师大版(2012)单元质检卷(B卷)(含解析)
文档属性
| 名称 | 第四章 一次函数—八年级上册数学北师大版(2012)单元质检卷(B卷)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-08 21:50:23 | ||
图片预览




文档简介
(8)一次函数—八年级上册数学北师大版(2012)单元质检卷(B卷)
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.函数中,自变量x的取值范围是( )
A. B. C. D.
2.直线如图所示,过点作与它平行的直线,则k,b的值是( )
A., B.,
C., D.,
3.已知,是关于x的函数图象上的两点,当时,,则m的取值范围是( )
A. B. C. D.
4.如图是某男生和某女生从小学到高中身高变化情况统计图,则对于这两人的身高年增长速度的说法不正确的是( )
A.男生在岁增长速度最快
B.女生在10岁增长速度最快
C.男生身高年增长速度能达到7厘米/年
D.女生身高年增长速度能达到7厘米/年
5.关于一次函数的图象和性质,下列说法正确的是( )
A.y随x的增大而增大 B.图象经过第三象限
C.图象经过点 D.图象与y轴的交点是
6.函数的图象与函数的图象有两个交点,则m的取值范围(或取值)是( )
A. B. C. D.
7.函数的图象如图所示,点,在该图象上,下列判断正确的是( )
甲:,之间的大小关系为;
乙:将函数图像向上平移2个单位,再向右平移2个单位;得到的函数为
A.只有甲对 B.只有乙对 C.甲、乙都对 D.甲、乙都不对
8.如图,把放在直角坐标系内,其中,,点A、B的坐标分别为、,将沿x轴向右平移,当点C落在直线上时,线段BC扫过的面积为( ).
A.80 B.88 C.96 D.100
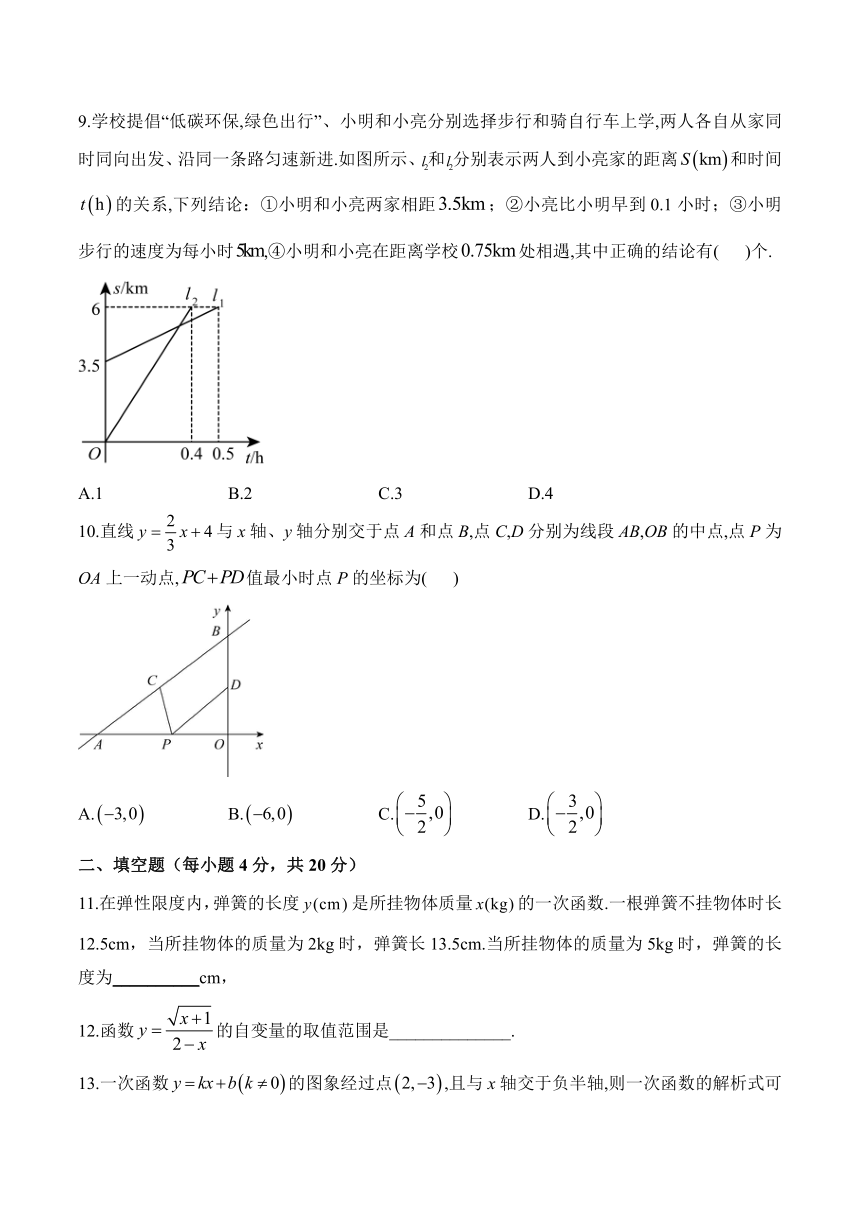
9.学校提倡“低碳环保,绿色出行”、小明和小亮分别选择步行和骑自行车上学,两人各自从家同时同向出发、沿同一条路匀速新进.如图所示、和分别表示两人到小亮家的距离和时间的关系,下列结论:①小明和小亮两家相距;②小亮比小明早到0.1小时;③小明步行的速度为每小时,④小明和小亮在距离学校处相遇,其中正确的结论有( )个.
A.1 B.2 C.3 D.4
10.直线与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,值最小时点P的坐标为( )
A. B. C. D.
二、填空题(每小题4分,共20分)
11.在弹性限度内,弹簧的长度是所挂物体质量的一次函数.一根弹簧不挂物体时长12.5cm,当所挂物体的质量为2kg时,弹簧长13.5cm.当所挂物体的质量为5kg时,弹簧的长度为__________cm,
12.函数的自变量的取值范围是______________.
13.一次函数的图象经过点,且与x轴交于负半轴,则一次函数的解析式可以是______(写出一个即可).
14.如图,直线与x轴、y轴分别交于点A和点B,点C在线段上,将沿所在直线折叠后,点A恰好落在y轴上点D处,则点C的坐标为______.
15.一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,往返速度的大小不变,两车离甲地的距离与慢车行驶时间之间的函数关系如图所示.则下列结论:
①快车比慢车晚出发;
②快车速度是慢车速度的2倍;
③慢车从出发到两车第一次相遇时,所走的路程为;
④若两车第二次相遇地距乙地距离为,则.
其中正确的有________.(请填写序号)
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)已知直线()经过点.
(1)求该直线的函数关系式;
(2)求该直线与两坐标轴围成的三角形面积.
17.(8分)某经销商计划购进400斤普通包装和精品包装的柿饼进行售卖,这两种包装柿饼的进价和售价如下表:
品名 进价(元/斤) 售价(元/斤)
普通包装 11 15
精品包装 15 28
设该经销商购进普通包装的柿饼x斤,总利润为y元.
(1)求y与x之间的函数关系式;
(2)经过市场调研,该经销商决定购进精品包装的柿饼不大于普通包装的3倍,请问获利最大的进货方案及最大利润.
18.(10分)项目化学习
项目背景:某校为更好地开展劳动实践活动,在校园内开辟了一片小菜园,用来种植甲、乙两种菜苗.
项目主题:探究不同种菜苗高度与种植天数的关系.
研究步骤:(1)选定小菜园中土壤水平及光照时长相同的一块地,并选择甲、乙两种菜苗进行种植;
(2)从种植开始每隔两天记录一次数据;
(3)数据分析,形成结论.
数据记录:
已种菜苗天数x/天 0 2 4 6 8 10 …
甲种菜苗高度 6 9 12 15 18 21 …
乙种菜苗高度 15 16 17 18 19 20 …
初步分析:通过分析数据得两种菜苗的高度,(单位:)与已种菜苗天数均为一次函数关系.
问题解决:请根据上述材料完成下列问题.
(1)在平面直角坐标系中分别画出菜苗高度,(单位:)关于已种菜苗天数x(单位:天)的函数图象;
(2)求出关于x的函数关系式,并直接写出第18天甲种菜苗的高度;
(3)观察函数图象,据实践经验可得这两种菜苗均在菜苗高度达到左右时开花,请估计哪种菜苗先开花,并说明理由.
19.(10分)阅读下面材料:
我们知道一次函数(,k,b是常数)的图象是一条直线,到高中学习时,直线通常写成(,A,B,C是常数)的形式,点到直线的距离可用公式计算.
例如:求点到直线的距离.
∵
∴其中,,
∴点到直线的距离为:
根据以上材料解答下列问题:
(1)求点到直线的距离;
(2)如图,直线沿y轴向上平移2个单位得到另一条直线,求这两条平行直线之间的距离.
20.(12分)如图,平面直角坐标系中,直线与直线相交于点,与x轴、y轴分别交于点B、C.
(1)求点B、点C的坐标;
(2)点M在射线上,是否存在点M,使的面积是的面积的?若存在,求出点M的坐标.
21.(12分)如图,在平面直角坐标系中,直线与坐标轴相交于点,,点C是y轴上一点.
(1)求直线的表达式.
(2)如图1,连接,将沿翻折至,若点E恰好落在直线上,求点C的坐标.
(3)如图2,点在x轴的正半轴上,连接,将绕点F顺时针旋转至的位置,连接,请问有最小值吗?如果有,请求出来;如果没有,请说明理由.
答案以及解析
1.答案:C
解析:分母不等于0,所以,
故选C.
2.答案:B
解析:直线与直线平行,
,
把代入中可得,
,解得,
故,,
故选:B.
3.答案:C
解析:当时,,
随x的增大而增大,
,
解得:,
的取值范围是.
故选:C.
4.答案:D
解析:A、从图象中可知,男生在岁增长速度最快,此选项说法正确,不符合题意,
B、从图象中可知,女生在10岁增长速度最快,此选项说法正确,不符合题意,
C、从图象中可知,男生身高年增长速度能达到7厘米/年,此选项说法正确,不符合题意,
D、从图象中可知,女生在岁每年增长都小于7厘米,此选项说法不正确,符合题意,
故选:D.
5.答案:D
解析:A、,y随x的增大而减小,故不符合题意;
B、,,图象经过第一、二、四象限,故不符合题意;
C、当时,故不符合题意;
D、一次函数,图象与y轴的交点是,故符合题意;
故选:D.
6.答案:B
解析:如图,当经过点时,,
解得,
当经过点时,,
解得,
所以,两个函数图象有两个交点时,m的取值范围是.
故选:B.
7.答案:A
解析:,
y随x的增大而增大,
,
,
故甲对;
由得,当时,,
直线与y轴的交点为,
将函数图像向上平移2个单位,再向右平移2个单位,点平移后的对应点为,
设平移后的函数解析式为,把代入得,
,
解得,
平移后的函数解析式为,
故乙不对;
故选:A.
8.答案:B
解析:∵点A、B的坐标分别为、,
∴,
∵,,
∴,
∴C点纵坐标为:8,
∵将沿x轴向右平移,当点C落在直线上时,
∴时,,解得:,即A点向右平移个单位,
∴线段BC扫过的面积为:.
故选B.
9.答案:D
解析:由图知:小明和小亮两家相距,小亮比小明早到小时,
故①,②正确;
小明步行的速度为每小时,故③正确,
设的函数解析式为,
则,
解得,
的函数解析式为;
设的函数解析式为,
则,
解得,
的函数解析式为;
令,即,
解得,
出发0.35小时后两人相遇,此时小明和小克在距离学校处.
故④正确.
故答案为:D.
10.答案:D
解析:作点D关于x轴的对称点,连接交x轴于点P,此时值最小,如图所示.
令中,则,
点B的坐标为;
令中,则,解得:,
点A的坐标为.
点C、D分别为线段、的中点,
点,点.
点和点D关于x轴对称,
点的坐标为.
设直线的解析式为,
直线过点,,
有,解得:,
直线的解析式为.
令中,则,解得:,
点P的坐标为.
故选:D.
11.答案:
解析:设y与x的函数关系式为,
由题意,得,
解得:,
故y与x之间的关系式为:,
当时,.
故答案为:.
12.答案:且
解析:由题意知,,
解得且,
故答案为:且.
13.答案:
解析:一次函数的图象经过点,
,
一次函数的图象与x轴交于负半轴,
,
取,则,
解得,
所以一次函数的解析式可以是.
故答案为:.
14.答案:
解析:由折叠可得,,
∵直线,当时,,当时,,
∴,,
∴,,
∴,
∴,
∴,
设,
则,
∴,
在中,,
∴,
解得,
∴点C的坐标为,
故答案为:.
15.答案:①③④
解析:由图象可得,快车比慢车晚出发2h,故①正确;
快车的速度为
慢车的速度为
快车速度是慢车速度的3倍,故②错误;
设慢车行驶mh两车第一次相遇,则,
解得,
慢车所走的路程为,故③正确;
设慢车行驶nh两车第二次相遇,则,
解得,
此时慢车距乙地的距离为:
解得,
故④正确,
故答案为:①③④.
16.答案:(1)
(2)4
解析:(1)直线经过点,
,解得,
∴直线的函数关系式为;
(2)在中,令,得;
∴与y轴的交点为,
令,得,解得;
∴与x轴的交点为,
∴该直线与两坐标轴围成的三角形面积为.
17.答案:(1)
(2)购进普通柿饼100斤,精品柿饼斤时,经销商获得最大利润,最大利润为4300元
解析:(1)设该经销商购进普通包装的柿饼x斤,则:购进精品包装的柿饼为斤,由题意,得:
,
整理,得:;
(2)由题意,得:,
解得:;
∵,,
∴y随x的增大而减小,
∴当时,总利润最大,为:元,
∴当购进普通柿饼100斤,精品柿饼斤时,经销商获得最大利润,最大利润为4300元.
18.答案:(1)图见解析
(2)与x的函数关系式为,第18天甲种菜苗的高度为
(3)甲种菜苗先开花,理由见解析
解析:(1)作图如解图;
(2)设与x的函数关系式为,代入点,
得,解得,
∴与x的函数关系式为,
当时,,
∴第18天甲种菜苗的高度为
故答案为:与x的函数关系式为,第18天甲种菜苗的高度为,
(3)甲种菜苗先开花,理由如下:
由图象可知,当甲,乙两种菜苗高度相同时(即与的交点处)都未达到的高度,
达到相同高度后的图象始终在的图象上方,
∴甲种菜苗比乙种菜苗先达到高度,
故答案为:甲种菜苗先开花.
19.答案:(1)
(2)
解析:(1)∵,
∴,,
∵点,
∴.
∴点到到直线的距离为;
(2)直线沿y轴向上平移2个单位得到另一条直线为,
在直线上任意取一点P,
当时,.
∴.
∵直线,
∴
∴,
∴两平行线之间的距离为.
20.答案:(1),
(2)存在,或
解析:(1)将代入得,
∴,
将代入得,
∴,
∴;
(2)存在.设,因点M在射线上,故.
因点,则,
因点,则点A到y轴距离为8,点M到y轴距离为,
过点A作于点D(如图),则
,
∵,
∴,
∴,则.
∵,
∴,
∴点M的坐标为或.
21.答案:(1)
(2)
(3)有最小值,最小值为
解析:(1)设直线的表达式为,
把,代入可得
,
解得,
∴直线的表达式为;
(2)∵,,
∴,,
∴,,
∵将沿翻折至,
∴,
∴,
∴,
在中,,
∴,
解得,
∴;
(3)过G作于E,过E作于N,过G作于M,
∵
∴设解析式为,
∴设,,,
∴,,
∵将绕点F顺时针旋转至的位置,
∴,,
∵,
∴,
∴,
∵,,
∴,,
∴,
∴,,
∴,
∵,
∴,
整理得:
∴,解得
∴
∵
∴令,整理得
∴在直线上移动,
∴直线与x轴交点坐标,与y轴交点坐标,
∴,
∴,
过B作于H,则即为的最小值,
∴,
∴.
∴有最小值,最小值为.
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.函数中,自变量x的取值范围是( )
A. B. C. D.
2.直线如图所示,过点作与它平行的直线,则k,b的值是( )
A., B.,
C., D.,
3.已知,是关于x的函数图象上的两点,当时,,则m的取值范围是( )
A. B. C. D.
4.如图是某男生和某女生从小学到高中身高变化情况统计图,则对于这两人的身高年增长速度的说法不正确的是( )
A.男生在岁增长速度最快
B.女生在10岁增长速度最快
C.男生身高年增长速度能达到7厘米/年
D.女生身高年增长速度能达到7厘米/年
5.关于一次函数的图象和性质,下列说法正确的是( )
A.y随x的增大而增大 B.图象经过第三象限
C.图象经过点 D.图象与y轴的交点是
6.函数的图象与函数的图象有两个交点,则m的取值范围(或取值)是( )
A. B. C. D.
7.函数的图象如图所示,点,在该图象上,下列判断正确的是( )
甲:,之间的大小关系为;
乙:将函数图像向上平移2个单位,再向右平移2个单位;得到的函数为
A.只有甲对 B.只有乙对 C.甲、乙都对 D.甲、乙都不对
8.如图,把放在直角坐标系内,其中,,点A、B的坐标分别为、,将沿x轴向右平移,当点C落在直线上时,线段BC扫过的面积为( ).
A.80 B.88 C.96 D.100
9.学校提倡“低碳环保,绿色出行”、小明和小亮分别选择步行和骑自行车上学,两人各自从家同时同向出发、沿同一条路匀速新进.如图所示、和分别表示两人到小亮家的距离和时间的关系,下列结论:①小明和小亮两家相距;②小亮比小明早到0.1小时;③小明步行的速度为每小时,④小明和小亮在距离学校处相遇,其中正确的结论有( )个.
A.1 B.2 C.3 D.4
10.直线与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,值最小时点P的坐标为( )
A. B. C. D.
二、填空题(每小题4分,共20分)
11.在弹性限度内,弹簧的长度是所挂物体质量的一次函数.一根弹簧不挂物体时长12.5cm,当所挂物体的质量为2kg时,弹簧长13.5cm.当所挂物体的质量为5kg时,弹簧的长度为__________cm,
12.函数的自变量的取值范围是______________.
13.一次函数的图象经过点,且与x轴交于负半轴,则一次函数的解析式可以是______(写出一个即可).
14.如图,直线与x轴、y轴分别交于点A和点B,点C在线段上,将沿所在直线折叠后,点A恰好落在y轴上点D处,则点C的坐标为______.
15.一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,往返速度的大小不变,两车离甲地的距离与慢车行驶时间之间的函数关系如图所示.则下列结论:
①快车比慢车晚出发;
②快车速度是慢车速度的2倍;
③慢车从出发到两车第一次相遇时,所走的路程为;
④若两车第二次相遇地距乙地距离为,则.
其中正确的有________.(请填写序号)
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)已知直线()经过点.
(1)求该直线的函数关系式;
(2)求该直线与两坐标轴围成的三角形面积.
17.(8分)某经销商计划购进400斤普通包装和精品包装的柿饼进行售卖,这两种包装柿饼的进价和售价如下表:
品名 进价(元/斤) 售价(元/斤)
普通包装 11 15
精品包装 15 28
设该经销商购进普通包装的柿饼x斤,总利润为y元.
(1)求y与x之间的函数关系式;
(2)经过市场调研,该经销商决定购进精品包装的柿饼不大于普通包装的3倍,请问获利最大的进货方案及最大利润.
18.(10分)项目化学习
项目背景:某校为更好地开展劳动实践活动,在校园内开辟了一片小菜园,用来种植甲、乙两种菜苗.
项目主题:探究不同种菜苗高度与种植天数的关系.
研究步骤:(1)选定小菜园中土壤水平及光照时长相同的一块地,并选择甲、乙两种菜苗进行种植;
(2)从种植开始每隔两天记录一次数据;
(3)数据分析,形成结论.
数据记录:
已种菜苗天数x/天 0 2 4 6 8 10 …
甲种菜苗高度 6 9 12 15 18 21 …
乙种菜苗高度 15 16 17 18 19 20 …
初步分析:通过分析数据得两种菜苗的高度,(单位:)与已种菜苗天数均为一次函数关系.
问题解决:请根据上述材料完成下列问题.
(1)在平面直角坐标系中分别画出菜苗高度,(单位:)关于已种菜苗天数x(单位:天)的函数图象;
(2)求出关于x的函数关系式,并直接写出第18天甲种菜苗的高度;
(3)观察函数图象,据实践经验可得这两种菜苗均在菜苗高度达到左右时开花,请估计哪种菜苗先开花,并说明理由.
19.(10分)阅读下面材料:
我们知道一次函数(,k,b是常数)的图象是一条直线,到高中学习时,直线通常写成(,A,B,C是常数)的形式,点到直线的距离可用公式计算.
例如:求点到直线的距离.
∵
∴其中,,
∴点到直线的距离为:
根据以上材料解答下列问题:
(1)求点到直线的距离;
(2)如图,直线沿y轴向上平移2个单位得到另一条直线,求这两条平行直线之间的距离.
20.(12分)如图,平面直角坐标系中,直线与直线相交于点,与x轴、y轴分别交于点B、C.
(1)求点B、点C的坐标;
(2)点M在射线上,是否存在点M,使的面积是的面积的?若存在,求出点M的坐标.
21.(12分)如图,在平面直角坐标系中,直线与坐标轴相交于点,,点C是y轴上一点.
(1)求直线的表达式.
(2)如图1,连接,将沿翻折至,若点E恰好落在直线上,求点C的坐标.
(3)如图2,点在x轴的正半轴上,连接,将绕点F顺时针旋转至的位置,连接,请问有最小值吗?如果有,请求出来;如果没有,请说明理由.
答案以及解析
1.答案:C
解析:分母不等于0,所以,
故选C.
2.答案:B
解析:直线与直线平行,
,
把代入中可得,
,解得,
故,,
故选:B.
3.答案:C
解析:当时,,
随x的增大而增大,
,
解得:,
的取值范围是.
故选:C.
4.答案:D
解析:A、从图象中可知,男生在岁增长速度最快,此选项说法正确,不符合题意,
B、从图象中可知,女生在10岁增长速度最快,此选项说法正确,不符合题意,
C、从图象中可知,男生身高年增长速度能达到7厘米/年,此选项说法正确,不符合题意,
D、从图象中可知,女生在岁每年增长都小于7厘米,此选项说法不正确,符合题意,
故选:D.
5.答案:D
解析:A、,y随x的增大而减小,故不符合题意;
B、,,图象经过第一、二、四象限,故不符合题意;
C、当时,故不符合题意;
D、一次函数,图象与y轴的交点是,故符合题意;
故选:D.
6.答案:B
解析:如图,当经过点时,,
解得,
当经过点时,,
解得,
所以,两个函数图象有两个交点时,m的取值范围是.
故选:B.
7.答案:A
解析:,
y随x的增大而增大,
,
,
故甲对;
由得,当时,,
直线与y轴的交点为,
将函数图像向上平移2个单位,再向右平移2个单位,点平移后的对应点为,
设平移后的函数解析式为,把代入得,
,
解得,
平移后的函数解析式为,
故乙不对;
故选:A.
8.答案:B
解析:∵点A、B的坐标分别为、,
∴,
∵,,
∴,
∴C点纵坐标为:8,
∵将沿x轴向右平移,当点C落在直线上时,
∴时,,解得:,即A点向右平移个单位,
∴线段BC扫过的面积为:.
故选B.
9.答案:D
解析:由图知:小明和小亮两家相距,小亮比小明早到小时,
故①,②正确;
小明步行的速度为每小时,故③正确,
设的函数解析式为,
则,
解得,
的函数解析式为;
设的函数解析式为,
则,
解得,
的函数解析式为;
令,即,
解得,
出发0.35小时后两人相遇,此时小明和小克在距离学校处.
故④正确.
故答案为:D.
10.答案:D
解析:作点D关于x轴的对称点,连接交x轴于点P,此时值最小,如图所示.
令中,则,
点B的坐标为;
令中,则,解得:,
点A的坐标为.
点C、D分别为线段、的中点,
点,点.
点和点D关于x轴对称,
点的坐标为.
设直线的解析式为,
直线过点,,
有,解得:,
直线的解析式为.
令中,则,解得:,
点P的坐标为.
故选:D.
11.答案:
解析:设y与x的函数关系式为,
由题意,得,
解得:,
故y与x之间的关系式为:,
当时,.
故答案为:.
12.答案:且
解析:由题意知,,
解得且,
故答案为:且.
13.答案:
解析:一次函数的图象经过点,
,
一次函数的图象与x轴交于负半轴,
,
取,则,
解得,
所以一次函数的解析式可以是.
故答案为:.
14.答案:
解析:由折叠可得,,
∵直线,当时,,当时,,
∴,,
∴,,
∴,
∴,
∴,
设,
则,
∴,
在中,,
∴,
解得,
∴点C的坐标为,
故答案为:.
15.答案:①③④
解析:由图象可得,快车比慢车晚出发2h,故①正确;
快车的速度为
慢车的速度为
快车速度是慢车速度的3倍,故②错误;
设慢车行驶mh两车第一次相遇,则,
解得,
慢车所走的路程为,故③正确;
设慢车行驶nh两车第二次相遇,则,
解得,
此时慢车距乙地的距离为:
解得,
故④正确,
故答案为:①③④.
16.答案:(1)
(2)4
解析:(1)直线经过点,
,解得,
∴直线的函数关系式为;
(2)在中,令,得;
∴与y轴的交点为,
令,得,解得;
∴与x轴的交点为,
∴该直线与两坐标轴围成的三角形面积为.
17.答案:(1)
(2)购进普通柿饼100斤,精品柿饼斤时,经销商获得最大利润,最大利润为4300元
解析:(1)设该经销商购进普通包装的柿饼x斤,则:购进精品包装的柿饼为斤,由题意,得:
,
整理,得:;
(2)由题意,得:,
解得:;
∵,,
∴y随x的增大而减小,
∴当时,总利润最大,为:元,
∴当购进普通柿饼100斤,精品柿饼斤时,经销商获得最大利润,最大利润为4300元.
18.答案:(1)图见解析
(2)与x的函数关系式为,第18天甲种菜苗的高度为
(3)甲种菜苗先开花,理由见解析
解析:(1)作图如解图;
(2)设与x的函数关系式为,代入点,
得,解得,
∴与x的函数关系式为,
当时,,
∴第18天甲种菜苗的高度为
故答案为:与x的函数关系式为,第18天甲种菜苗的高度为,
(3)甲种菜苗先开花,理由如下:
由图象可知,当甲,乙两种菜苗高度相同时(即与的交点处)都未达到的高度,
达到相同高度后的图象始终在的图象上方,
∴甲种菜苗比乙种菜苗先达到高度,
故答案为:甲种菜苗先开花.
19.答案:(1)
(2)
解析:(1)∵,
∴,,
∵点,
∴.
∴点到到直线的距离为;
(2)直线沿y轴向上平移2个单位得到另一条直线为,
在直线上任意取一点P,
当时,.
∴.
∵直线,
∴
∴,
∴两平行线之间的距离为.
20.答案:(1),
(2)存在,或
解析:(1)将代入得,
∴,
将代入得,
∴,
∴;
(2)存在.设,因点M在射线上,故.
因点,则,
因点,则点A到y轴距离为8,点M到y轴距离为,
过点A作于点D(如图),则
,
∵,
∴,
∴,则.
∵,
∴,
∴点M的坐标为或.
21.答案:(1)
(2)
(3)有最小值,最小值为
解析:(1)设直线的表达式为,
把,代入可得
,
解得,
∴直线的表达式为;
(2)∵,,
∴,,
∴,,
∵将沿翻折至,
∴,
∴,
∴,
在中,,
∴,
解得,
∴;
(3)过G作于E,过E作于N,过G作于M,
∵
∴设解析式为,
∴设,,,
∴,,
∵将绕点F顺时针旋转至的位置,
∴,,
∵,
∴,
∴,
∵,,
∴,,
∴,
∴,,
∴,
∵,
∴,
整理得:
∴,解得
∴
∵
∴令,整理得
∴在直线上移动,
∴直线与x轴交点坐标,与y轴交点坐标,
∴,
∴,
过B作于H,则即为的最小值,
∴,
∴.
∴有最小值,最小值为.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
