三角形的面积重难点应用题专项训练(含解析)-数学五年级上册苏教版
文档属性
| 名称 | 三角形的面积重难点应用题专项训练(含解析)-数学五年级上册苏教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 584.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-09 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
三角形的面积重难点应用题专项训练-数学五年级上册苏教版
一、解答题
1.如图,学校在围墙的一角靠墙用篱笆建了一个直角三角形花坛,需要多长的篱笆?
2.一块三角形湿地,底是10千米,高6000米。如果每平方千米能栖息30000只水鸟,这块湿地共能栖息多少万只水鸟?
3.东井村的土地是一个近似的三角形,该村的土地面积大约是多少平方千米?
4.一面直角三角形小红旗,它的两条直角边的长度都是14cm,做100面这样的小红旗,要用多少平方米的纸?
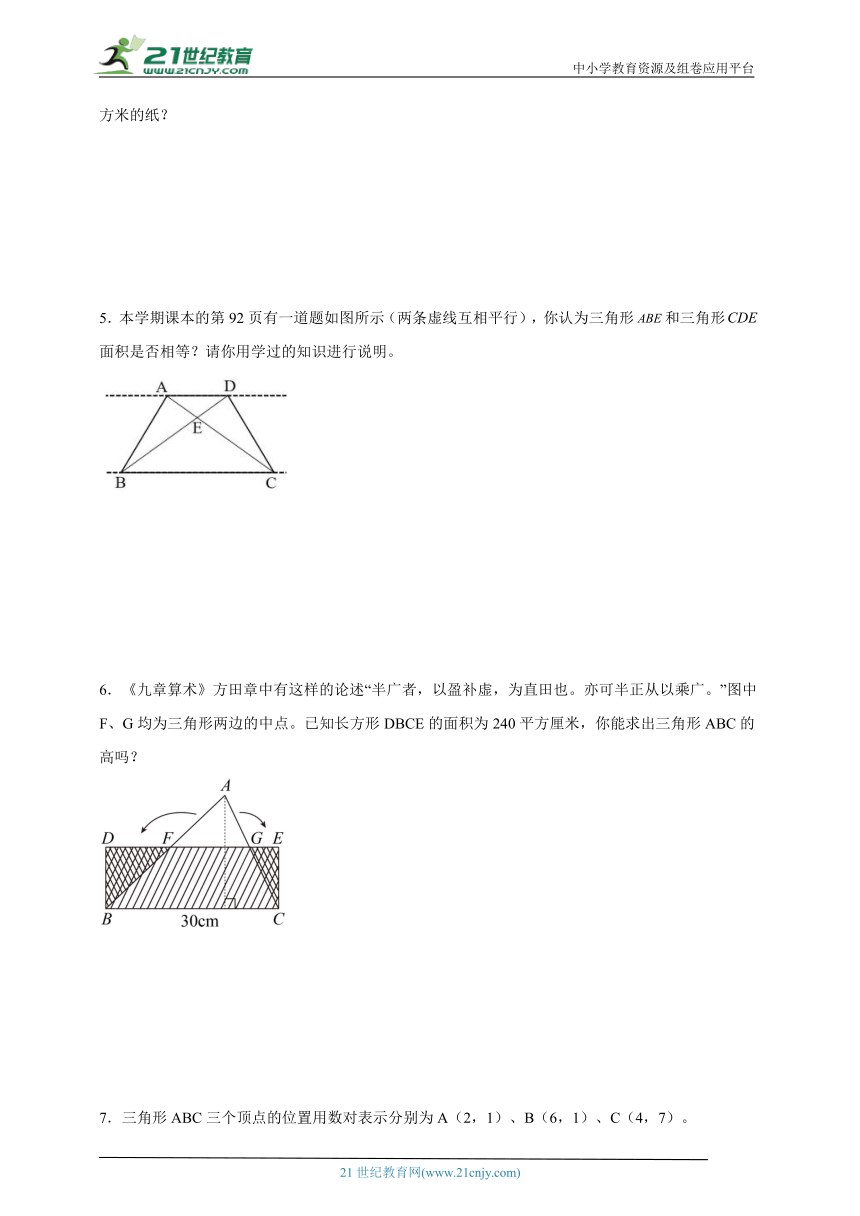
5.本学期课本的第92页有一道题如图所示(两条虚线互相平行),你认为三角形和三角形面积是否相等?请你用学过的知识进行说明。
6.《九章算术》方田章中有这样的论述“半广者,以盈补虚,为直田也。亦可半正从以乘广。”图中F、G均为三角形两边的中点。已知长方形DBCE的面积为240平方厘米,你能求出三角形ABC的高吗?
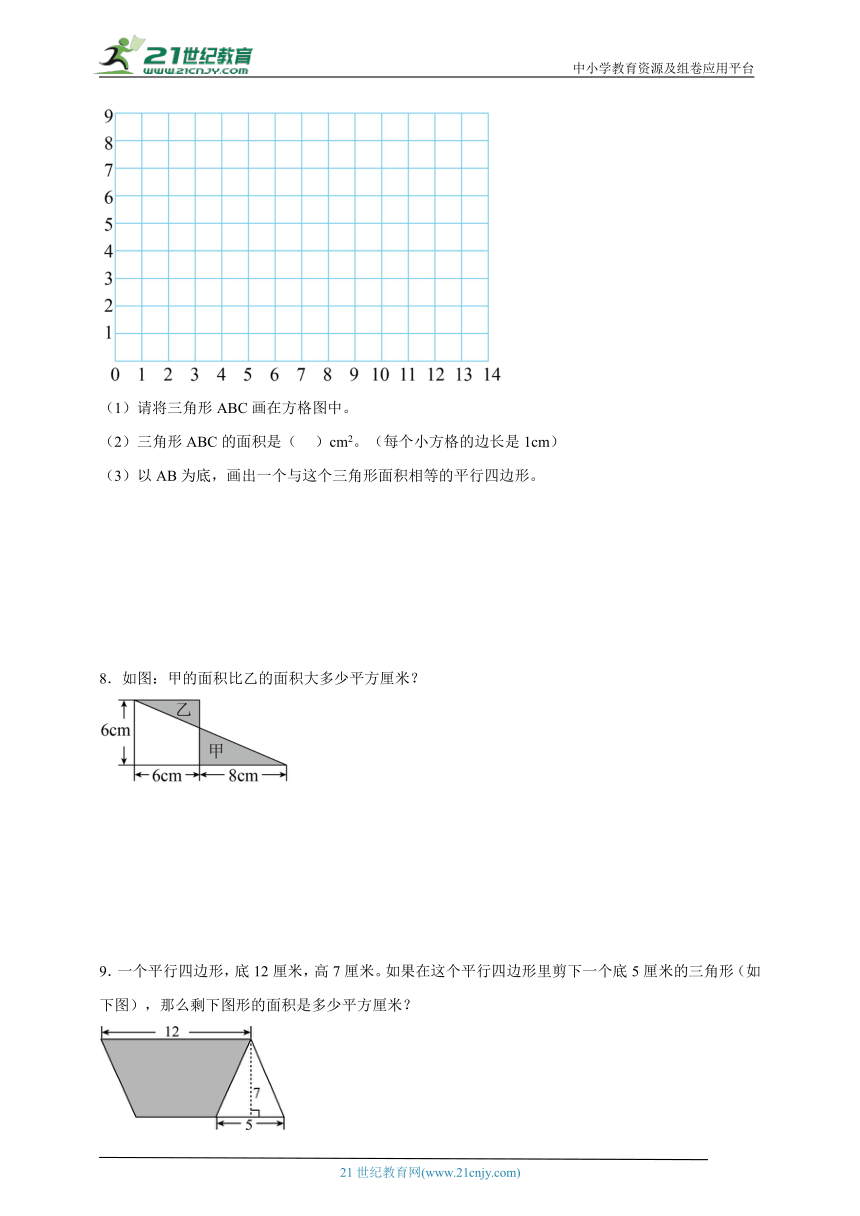
7.三角形ABC三个顶点的位置用数对表示分别为A(2,1)、B(6,1)、C(4,7)。
(1)请将三角形ABC画在方格图中。
(2)三角形ABC的面积是( )cm2。(每个小方格的边长是1cm)
(3)以AB为底,画出一个与这个三角形面积相等的平行四边形。
8.如图:甲的面积比乙的面积大多少平方厘米?
9.一个平行四边形,底12厘米,高7厘米。如果在这个平行四边形里剪下一个底5厘米的三角形(如下图),那么剩下图形的面积是多少平方厘米?
10.校园里有一块长10米、宽6米的长方形地(如图),学校打算在这块地上划出一块底和高都是6米的三角形地种红花,其它地种绿草。请你在示意图上画出你的设计,并求出绿草的占地面积。
11.如图,点A是平行四边形底的中点,将这块平行四边形土地分成两部分,分别种上青菜和水果,种植水果的面积是90平方米。这块平行四边形土地的面积是多少平方米?
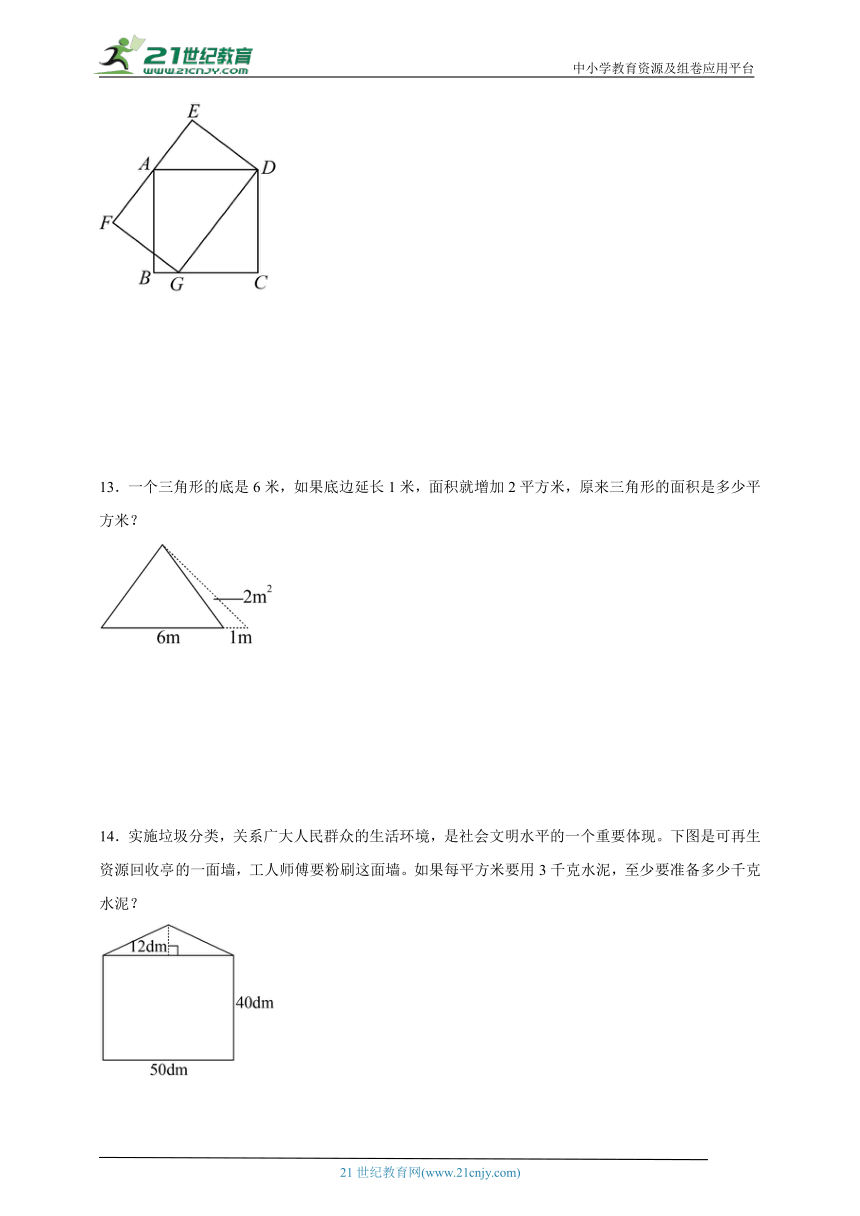
12.小健平时很喜欢研究数学中的图形。有一天他把一个长方形和一个正方形重叠在一起(如下图)。如果正方形ABCD的边长是8厘米,长方形DEFG的长厘米,你能算出它的宽DE长多少厘米吗?
13.一个三角形的底是6米,如果底边延长1米,面积就增加2平方米,原来三角形的面积是多少平方米?
14.实施垃圾分类,关系广大人民群众的生活环境,是社会文明水平的一个重要体现。下图是可再生资源回收亭的一面墙,工人师傅要粉刷这面墙。如果每平方米要用3千克水泥,至少要准备多少千克水泥?
15.随着科学技术的发展进步,城市建设也融入了许多先进、智能的元素。郑州市地铁在部分站点设置了投影导向,能更加醒目地向大家传递信息。请根据图中的数据算一算,B出口的投影导向图的面积是多少?
16.一块某地由两部分组成(如图),长方形部分种黄瓜,等腰三角形部分种豆角。黄瓜地的面积是180平方米,豆角地的面积是多少平方米?
参考答案:
1.25米
【分析】据观察发现篱笆和墙角围成了一个直角三角形,根据,可以先把一条直角边看成底,另一条直角边看成高,求出三角形的面积,已知斜边上的高是12米再根据三角形面积×2÷高=底,这个底边就是所求的三角形的斜边。
【详解】
(平方米)
(米)
答:需要25米长的篱笆。
2.90万只
【分析】由题意得,这个三角形湿地,底是10千米,高6000米。可以先把6000米转化为多少千米,再根据三角形的面积=底×高÷2算出三角形的面积。每平方千米能栖息30000只水鸟,再乘上30000即可算出这块湿地一共能栖息多少万只水鸟。
【详解】6000米=6千米
10×6÷2
=60÷2
=30(平方千米)
30×30000=900000(只)=90(万只)
答:这块湿地共能栖息90万只水鸟。
3.18平方千米
【分析】根据三角形面积=底×高÷2,据此代入数据计算出该村的土地面积大约是多少平方米,根据1平方千米=1000000平方米,换算成平方千米为单位即可。
【详解】7500×4800÷2
=36000000÷2
=18000000(平方米)
18000000平方米=18平方千米
答:该村的土地面积大约是18平方千米。
4.0.98平方米
【分析】直角三角形的面积=底×高÷2。这面小红旗的两条直角边长度都是14厘米,所以一面小红旗的面积为14×14÷2=98平方厘米。要做100面这样的小红旗,总面积就是一面小红旗面积乘100,据此解答。
【详解】一面小红旗的面积:14×14÷2=98(平方厘米);
100面小红旗的总面积:98×100=9800(平方厘米);
因为1平方米=10000平方厘米,所以9800平方厘米=0.98平方米;
答:做100面这样的小红旗,要用0.98平方米的纸。
5.相等,说明见详解
【分析】等底等高的三角形面积相等,而平行线之间的距离都相等,因为三角形ABD与三角形ACD是等底等高的三角形,根据三角形面积公式:面积=底×高÷2,确定三角形面积形ABD与三角形ACD的面积之间的关系,进而求出三角形ABE与三角形CDE的关系(答案不唯一)。
【详解】根据分析可知,三角形ABD与三角形ACD是等底等高的三角形,
所以三角形ABD面积=三角形ACD面积。
三角形ABE的面积=三角形ABD的面积-三角形ADE的面积;
三角形CDE的面积=三角形ACD的面积-三角形ADE的面积;
三角形ABD的面积=三角形ACD的面积,
两个三角形都减去同一个三角形,所以三角形ABE的面积=三角形CDE的面积。
6.16厘米
【分析】根据题图可知,把三角形转化为长方形后面积不变,这个长方形的长等于三角形的底,这个长方形的宽等于三角形高的一半,根据长方形的面积=长×宽,那么宽=面积÷长,求出长方形的宽,然后用长方形的宽乘2就是三角形的高。据此解答即可。
【详解】240÷30×2
=8×2
=16(厘米)
答:三角形ABC的高为16厘米。
7.(1)(3)图见详解
(2)12
【分析】(1)用数对表示位置时,括号里第一个数字表示列,第二个数字表示行,据此找到点的位置,再将各点一次连接成图形即可。
(2)数出三角形底和高的方格数,可以知道它们的长度,再根据三角形面积=底×高÷2,进行计算即可。
(3)平行四边形面积=底×高,底不变与它面积相等的三角形的高是平行四边形高的2倍,据此解答。
【详解】(2)4×6÷2=12(cm2)
三角形ABC的面积是12cm2。
(3)由分析得:6÷2=3(cm)
以AB为底,画出一个与这个三角形面积相等的平行四边形的高为3cm。
(1)(3)如下图:
8.6平方厘米
【分析】观察图形可知,甲的面积=底是6厘米,高是(6+8)厘米的三角形面积-左下角空白面积;乙的面积=边长是6厘米正方形面积-左下角空白面积,由此可知,求甲的面积比乙的面积大多少平方厘米,即甲的面积-乙的面积=底是6厘米,高是(6+8)厘米的三角形面积-边长是6厘米的正方形面积,根据三角形面积公式:面积=底×高÷2,正方形面积公式:面积=边长×边长,代入数据,即可解答。
【详解】6×(6+8)÷2-6×6
=6×14÷2-36
=84÷2-36
=42-36
=6(平方厘米)
答:甲的面积比乙的面积大6平方厘米。
9.66.5平方厘米
【分析】根据图,可知,剩下的面积为平行四边形面积-剪下的三角形面积,根据平行四边形面积公式:S=底×高,三角形面积公式:S=底×高÷2,将数据代入求解即可。
【详解】由分析可得:
12×7-5×7÷2
=84-35÷2
=84-17.5
=66.5(平方厘米)
答:剩下图形的面积是66.5平方厘米。
10.图见详解;42平方米
【分析】长方形地的宽是6米,在这块地上画出一块底和高都是6米的三角形,可用长方形的宽6米作为这个三角形的底,在长方形中长垂直于宽,可在长上截取6米作为这个三角形的高,连接截取6米长的点与宽的另一个端点画成一个等腰直角三角形即可。用长方形的面积减去这个三角形的面积,就是剩下的面积,即绿草的占地面积。长方形的面积=长×宽,三角形的面积=底×高÷2。
【详解】
设计(答案不唯一)
10×6-6×6÷2
=60-36÷2
=60-18
=42(平方米)
答:绿草的占地面积是42平方米。
11.360平方米
【分析】根据“三角形的面积=底×高÷2”可知:底=三角形的面积×2÷高,种植水果的三角形地的面积是90平方米,高是12米,用90×2÷12可求出三角形的底是15米;又因为点A是平行四边形底的中点,所以平行四边形的底是15×2=30(米);最后根据平行四边形的面积=底×高,用30×12可求出这块平行四边形土地的面积。
【详解】90×2÷12
=180÷12
=15(米)
15×2×12
=30×12
=360(平方米)
答:这块平行四边形土地的面积是360平方米。
12.6.4厘米
【分析】如下图:连接AG,根据三角形ADG等于正方形ABCD面积的一半,用8×8÷2可求出三角形ADG的面积是32平方厘米,而三角形ADG的面积也等于10×DE÷2,据此用32×2÷10可求出DE的长。
【详解】8×8÷2×2÷10
=64÷2×2÷10
=32×2÷10
=64÷10
=6.4(厘米)
答:它的宽DE长6.4厘米。
13.12平方米
【分析】延长出来的三角形与原来三角形等高,根据三角形的高=面积×2÷底,先求出三角形的高,再利用三角形面积=底×高÷2,列式解答即可。
【详解】2×2÷1=4(米)
6×4÷2=12(平方米)
答:原来三角形的面积是12平方米。
14.69千克
【分析】这面墙的上部是一个底是50分米,高是12分米的三角形,下部是一个长是50分米,宽是40分米的长方形。根据三角形的面积=底×高÷2,用50×12÷2可求出三角形的面积是300平方分米;根据长方形的面积=长×宽,用50×40可求出长方形的面积是2000平方分米;再用三角形的面积加上长方形的面积求出这面墙的总面积是2300平方分米;2300平方分米=23平方米,最后用每平方米用的水泥的千克数(3千克)乘这面墙的总面积(23平方米)可求出至少要准备的水泥的千克数。
【详解】50×12÷2+50×40
=600÷2+2000
=300+2000
=2300(平方分米)
2300平方分米=23平方米
23×3=69(千克)
答:至少要准备69千克水泥。
15.130平方分米
【分析】看图可知,投影导向图可以分成一个长方形加上一个三角形,根据长方形的面积公式:长×宽;三角形的面积公式:(底×高)÷2,两者面积加起来即可求出投影导向图的面积。
【详解】长方形的面积:10×9=90(平方分米)
三角形的面积:16×5÷2
=80÷2
=40(平方分米)
90+40=130(平方分米)
答:B出口的投影导向图的面积是130平方分米。
【点睛】此题考查了学生对三角形的面积公式以及长方形的面积公式的熟练掌握程度。
16.72平方米
【分析】根据长方形的面积公式可知,用黄瓜地的面积180平方米除以长方形的长15米,即可求出长方形的宽为12米,根据等腰直角三角形的特征可知,这个三角形的两条直角边相等,都是12米,利用三角形的面积公式,列式:12×12÷2即可求出豆角地的面积是多少平方米。
【详解】180÷15=12(米)
12×12÷2
=144÷2
=72(平方米)
答:豆角地的面积是72平方米。
【点睛】此题主要是理解等腰直角三角形的特征,灵活运用长方形和三角形的面积公式求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
三角形的面积重难点应用题专项训练-数学五年级上册苏教版
一、解答题
1.如图,学校在围墙的一角靠墙用篱笆建了一个直角三角形花坛,需要多长的篱笆?
2.一块三角形湿地,底是10千米,高6000米。如果每平方千米能栖息30000只水鸟,这块湿地共能栖息多少万只水鸟?
3.东井村的土地是一个近似的三角形,该村的土地面积大约是多少平方千米?
4.一面直角三角形小红旗,它的两条直角边的长度都是14cm,做100面这样的小红旗,要用多少平方米的纸?
5.本学期课本的第92页有一道题如图所示(两条虚线互相平行),你认为三角形和三角形面积是否相等?请你用学过的知识进行说明。
6.《九章算术》方田章中有这样的论述“半广者,以盈补虚,为直田也。亦可半正从以乘广。”图中F、G均为三角形两边的中点。已知长方形DBCE的面积为240平方厘米,你能求出三角形ABC的高吗?
7.三角形ABC三个顶点的位置用数对表示分别为A(2,1)、B(6,1)、C(4,7)。
(1)请将三角形ABC画在方格图中。
(2)三角形ABC的面积是( )cm2。(每个小方格的边长是1cm)
(3)以AB为底,画出一个与这个三角形面积相等的平行四边形。
8.如图:甲的面积比乙的面积大多少平方厘米?
9.一个平行四边形,底12厘米,高7厘米。如果在这个平行四边形里剪下一个底5厘米的三角形(如下图),那么剩下图形的面积是多少平方厘米?
10.校园里有一块长10米、宽6米的长方形地(如图),学校打算在这块地上划出一块底和高都是6米的三角形地种红花,其它地种绿草。请你在示意图上画出你的设计,并求出绿草的占地面积。
11.如图,点A是平行四边形底的中点,将这块平行四边形土地分成两部分,分别种上青菜和水果,种植水果的面积是90平方米。这块平行四边形土地的面积是多少平方米?
12.小健平时很喜欢研究数学中的图形。有一天他把一个长方形和一个正方形重叠在一起(如下图)。如果正方形ABCD的边长是8厘米,长方形DEFG的长厘米,你能算出它的宽DE长多少厘米吗?
13.一个三角形的底是6米,如果底边延长1米,面积就增加2平方米,原来三角形的面积是多少平方米?
14.实施垃圾分类,关系广大人民群众的生活环境,是社会文明水平的一个重要体现。下图是可再生资源回收亭的一面墙,工人师傅要粉刷这面墙。如果每平方米要用3千克水泥,至少要准备多少千克水泥?
15.随着科学技术的发展进步,城市建设也融入了许多先进、智能的元素。郑州市地铁在部分站点设置了投影导向,能更加醒目地向大家传递信息。请根据图中的数据算一算,B出口的投影导向图的面积是多少?
16.一块某地由两部分组成(如图),长方形部分种黄瓜,等腰三角形部分种豆角。黄瓜地的面积是180平方米,豆角地的面积是多少平方米?
参考答案:
1.25米
【分析】据观察发现篱笆和墙角围成了一个直角三角形,根据,可以先把一条直角边看成底,另一条直角边看成高,求出三角形的面积,已知斜边上的高是12米再根据三角形面积×2÷高=底,这个底边就是所求的三角形的斜边。
【详解】
(平方米)
(米)
答:需要25米长的篱笆。
2.90万只
【分析】由题意得,这个三角形湿地,底是10千米,高6000米。可以先把6000米转化为多少千米,再根据三角形的面积=底×高÷2算出三角形的面积。每平方千米能栖息30000只水鸟,再乘上30000即可算出这块湿地一共能栖息多少万只水鸟。
【详解】6000米=6千米
10×6÷2
=60÷2
=30(平方千米)
30×30000=900000(只)=90(万只)
答:这块湿地共能栖息90万只水鸟。
3.18平方千米
【分析】根据三角形面积=底×高÷2,据此代入数据计算出该村的土地面积大约是多少平方米,根据1平方千米=1000000平方米,换算成平方千米为单位即可。
【详解】7500×4800÷2
=36000000÷2
=18000000(平方米)
18000000平方米=18平方千米
答:该村的土地面积大约是18平方千米。
4.0.98平方米
【分析】直角三角形的面积=底×高÷2。这面小红旗的两条直角边长度都是14厘米,所以一面小红旗的面积为14×14÷2=98平方厘米。要做100面这样的小红旗,总面积就是一面小红旗面积乘100,据此解答。
【详解】一面小红旗的面积:14×14÷2=98(平方厘米);
100面小红旗的总面积:98×100=9800(平方厘米);
因为1平方米=10000平方厘米,所以9800平方厘米=0.98平方米;
答:做100面这样的小红旗,要用0.98平方米的纸。
5.相等,说明见详解
【分析】等底等高的三角形面积相等,而平行线之间的距离都相等,因为三角形ABD与三角形ACD是等底等高的三角形,根据三角形面积公式:面积=底×高÷2,确定三角形面积形ABD与三角形ACD的面积之间的关系,进而求出三角形ABE与三角形CDE的关系(答案不唯一)。
【详解】根据分析可知,三角形ABD与三角形ACD是等底等高的三角形,
所以三角形ABD面积=三角形ACD面积。
三角形ABE的面积=三角形ABD的面积-三角形ADE的面积;
三角形CDE的面积=三角形ACD的面积-三角形ADE的面积;
三角形ABD的面积=三角形ACD的面积,
两个三角形都减去同一个三角形,所以三角形ABE的面积=三角形CDE的面积。
6.16厘米
【分析】根据题图可知,把三角形转化为长方形后面积不变,这个长方形的长等于三角形的底,这个长方形的宽等于三角形高的一半,根据长方形的面积=长×宽,那么宽=面积÷长,求出长方形的宽,然后用长方形的宽乘2就是三角形的高。据此解答即可。
【详解】240÷30×2
=8×2
=16(厘米)
答:三角形ABC的高为16厘米。
7.(1)(3)图见详解
(2)12
【分析】(1)用数对表示位置时,括号里第一个数字表示列,第二个数字表示行,据此找到点的位置,再将各点一次连接成图形即可。
(2)数出三角形底和高的方格数,可以知道它们的长度,再根据三角形面积=底×高÷2,进行计算即可。
(3)平行四边形面积=底×高,底不变与它面积相等的三角形的高是平行四边形高的2倍,据此解答。
【详解】(2)4×6÷2=12(cm2)
三角形ABC的面积是12cm2。
(3)由分析得:6÷2=3(cm)
以AB为底,画出一个与这个三角形面积相等的平行四边形的高为3cm。
(1)(3)如下图:
8.6平方厘米
【分析】观察图形可知,甲的面积=底是6厘米,高是(6+8)厘米的三角形面积-左下角空白面积;乙的面积=边长是6厘米正方形面积-左下角空白面积,由此可知,求甲的面积比乙的面积大多少平方厘米,即甲的面积-乙的面积=底是6厘米,高是(6+8)厘米的三角形面积-边长是6厘米的正方形面积,根据三角形面积公式:面积=底×高÷2,正方形面积公式:面积=边长×边长,代入数据,即可解答。
【详解】6×(6+8)÷2-6×6
=6×14÷2-36
=84÷2-36
=42-36
=6(平方厘米)
答:甲的面积比乙的面积大6平方厘米。
9.66.5平方厘米
【分析】根据图,可知,剩下的面积为平行四边形面积-剪下的三角形面积,根据平行四边形面积公式:S=底×高,三角形面积公式:S=底×高÷2,将数据代入求解即可。
【详解】由分析可得:
12×7-5×7÷2
=84-35÷2
=84-17.5
=66.5(平方厘米)
答:剩下图形的面积是66.5平方厘米。
10.图见详解;42平方米
【分析】长方形地的宽是6米,在这块地上画出一块底和高都是6米的三角形,可用长方形的宽6米作为这个三角形的底,在长方形中长垂直于宽,可在长上截取6米作为这个三角形的高,连接截取6米长的点与宽的另一个端点画成一个等腰直角三角形即可。用长方形的面积减去这个三角形的面积,就是剩下的面积,即绿草的占地面积。长方形的面积=长×宽,三角形的面积=底×高÷2。
【详解】
设计(答案不唯一)
10×6-6×6÷2
=60-36÷2
=60-18
=42(平方米)
答:绿草的占地面积是42平方米。
11.360平方米
【分析】根据“三角形的面积=底×高÷2”可知:底=三角形的面积×2÷高,种植水果的三角形地的面积是90平方米,高是12米,用90×2÷12可求出三角形的底是15米;又因为点A是平行四边形底的中点,所以平行四边形的底是15×2=30(米);最后根据平行四边形的面积=底×高,用30×12可求出这块平行四边形土地的面积。
【详解】90×2÷12
=180÷12
=15(米)
15×2×12
=30×12
=360(平方米)
答:这块平行四边形土地的面积是360平方米。
12.6.4厘米
【分析】如下图:连接AG,根据三角形ADG等于正方形ABCD面积的一半,用8×8÷2可求出三角形ADG的面积是32平方厘米,而三角形ADG的面积也等于10×DE÷2,据此用32×2÷10可求出DE的长。
【详解】8×8÷2×2÷10
=64÷2×2÷10
=32×2÷10
=64÷10
=6.4(厘米)
答:它的宽DE长6.4厘米。
13.12平方米
【分析】延长出来的三角形与原来三角形等高,根据三角形的高=面积×2÷底,先求出三角形的高,再利用三角形面积=底×高÷2,列式解答即可。
【详解】2×2÷1=4(米)
6×4÷2=12(平方米)
答:原来三角形的面积是12平方米。
14.69千克
【分析】这面墙的上部是一个底是50分米,高是12分米的三角形,下部是一个长是50分米,宽是40分米的长方形。根据三角形的面积=底×高÷2,用50×12÷2可求出三角形的面积是300平方分米;根据长方形的面积=长×宽,用50×40可求出长方形的面积是2000平方分米;再用三角形的面积加上长方形的面积求出这面墙的总面积是2300平方分米;2300平方分米=23平方米,最后用每平方米用的水泥的千克数(3千克)乘这面墙的总面积(23平方米)可求出至少要准备的水泥的千克数。
【详解】50×12÷2+50×40
=600÷2+2000
=300+2000
=2300(平方分米)
2300平方分米=23平方米
23×3=69(千克)
答:至少要准备69千克水泥。
15.130平方分米
【分析】看图可知,投影导向图可以分成一个长方形加上一个三角形,根据长方形的面积公式:长×宽;三角形的面积公式:(底×高)÷2,两者面积加起来即可求出投影导向图的面积。
【详解】长方形的面积:10×9=90(平方分米)
三角形的面积:16×5÷2
=80÷2
=40(平方分米)
90+40=130(平方分米)
答:B出口的投影导向图的面积是130平方分米。
【点睛】此题考查了学生对三角形的面积公式以及长方形的面积公式的熟练掌握程度。
16.72平方米
【分析】根据长方形的面积公式可知,用黄瓜地的面积180平方米除以长方形的长15米,即可求出长方形的宽为12米,根据等腰直角三角形的特征可知,这个三角形的两条直角边相等,都是12米,利用三角形的面积公式,列式:12×12÷2即可求出豆角地的面积是多少平方米。
【详解】180÷15=12(米)
12×12÷2
=144÷2
=72(平方米)
答:豆角地的面积是72平方米。
【点睛】此题主要是理解等腰直角三角形的特征,灵活运用长方形和三角形的面积公式求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
