山东省日照市东港区日照港中学2024-2025学年九年级上学期10月月考数学试卷(pdf版,无答案)
文档属性
| 名称 | 山东省日照市东港区日照港中学2024-2025学年九年级上学期10月月考数学试卷(pdf版,无答案) |  | |
| 格式 | |||
| 文件大小 | 572.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-09 15:40:43 | ||
图片预览


文档简介
日照港中学九年级单元检测数学试卷
一、单选题 (共 36分)
1.下列图形中,既是轴对称图形,又是中心对称图形的是 ( )
A. B. C. D.
2. 1已知抛物线 y=- x-3 2 + 2 下列说法正确的是 ( )
A.开口向上 B.对称轴是直线 x=-3
C. 1顶点坐标为 3, 2 D.当 x<-3时,y随 x的增大而减小
3. 若 α,β是方程 x2+ 2x- 2005= 0的两个实数根,则 α2+ 3α+ β的值为 ( )
A. 2005 B. 2003 C. - 2005 D. 4010
4. 已知:2是关于 x的方程 x2- (m + 1)x +m = 0的一个实数根,并且这个方程的两个实数根恰好是等腰
△ABC的两条边的边长,则△ABC的周长为 ( )
A. 6 B. 4 C. 5 D. 4或 5
5.函数 y= ax2- x+ 2和 y=-ax- a(a≠ 0)在同一平面直角坐标系中的图象可能是 ( )
A. B. C. D.
6.如图,把图中的△ABC经过旋转变换得到△A'B'C ',如果图中△ABC上的点P的坐标为 (a,b), 那么它的对应
点P'的坐标为 ( )
A. (a- 2,b) B. (a+ 2,b) C. (-a- 2, -b) D. (a+ 2, -b)
第 6题图 第 7题图
7.如图,两个全等的等腰直角△ABC和△DEF的斜边AB=DE= 10, 点E与点A重合,斜边AB与DE在一条
直线上,△ABC保持不动,△DEF以每秒 2个单位长度的速度向右运动,直到点D与点B重合时停止运动,设
运动时间为 x秒,两个等腰直角三角形重叠部分的面积为 y个平方单位,则 y与 x函数关系的图象大致是
( )
A. B. C. D.
·第1页·
{#{QQABDBQCEEsxgggCQAgAppTAAACAQA5hKCEwWGICwgKqQkBIGEgALAUQggsgOQgALAqAAoYAKIACCYAFFAABBKCAA==}#}#} }
8.若二次函数 y= x2+ 2x+ 1在m≤ x≤m+ 1(m为常数)的范围内有最小值 1,则m的值为 ( )
A. - 3或 0 B. - 2或 1 C. - 2或 0 D. - 3≤m≤-2
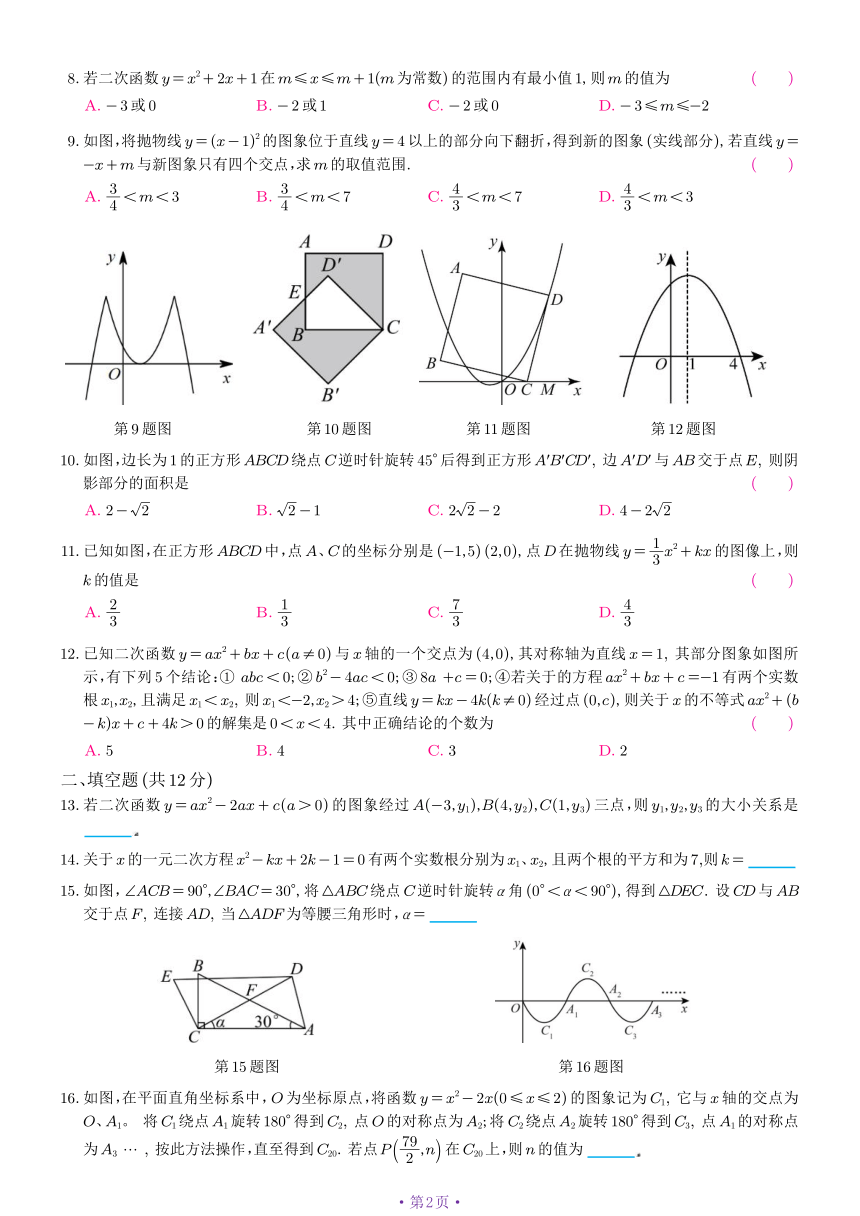
9.如图,将抛物线 y= (x- 1)2的图象位于直线 y= 4以上的部分向下翻折,得到新的图象 (实线部分),若直线 y=
-x+m与新图象只有四个交点,求m的取值范围. ( )
A. 34
3第 9题图 第 10题图 第 11题图 第 12题图
10.如图,边长为 1的正方形ABCD绕点C逆时针旋转 45°后得到正方形A'B'CD', 边A'D'与AB交于点E, 则阴
影部分的面积是 ( )
A. 2- 2 B. 2- 1 C. 2 2- 2 D. 4- 2 2
11.已知如图,在正方形ABCD中,点A、C的坐标分别是 (-1,5) (2,0),点D 1在抛物线 y= 23 x + kx的图像上,则
k的值是 ( )
A. 23 B.
1
3 C.
7
3 D.
4
3
12.已知二次函数 y= ax2+ bx+ c(a≠ 0)与 x轴的一个交点为 (4,0),其对称轴为直线 x= 1, 其部分图象如图所
示,有下列 5个结论:① abc< 0;② b2- 4ac< 0;③ 8a +c= 0;④若关于的方程 ax2+ bx+ c=-1有两个实数
根 x1,x2,且满足 x1< x2, 则 x1<-2,x2> 4;⑤直线 y= kx- 4k(k≠ 0)经过点 (0,c),则关于 x的不等式 ax2+ (b
- k)x+ c+ 4k> 0的解集是 0< x< 4. 其中正确结论的个数为 ( )
A. 5 B. 4 C. 3 D. 2
二、填空题 (共 12分)
13.若二次函数 y= ax2- 2ax+ c(a> 0)的图象经过A(-3,y1),B(4,y2),C(1,y3)三点,则 y1,y2,y3的大小关系是
14.关于 x的一元二次方程 x2- kx+ 2k- 1= 0有两个实数根分别为 x1、x2,且两个根的平方和为 7,则 k=
15.如图,∠ACB= 90°,∠BAC= 30°,将△ABC绕点C逆时针旋转 α角 (0° < α< 90°),得到△DEC. 设CD与AB
交于点F, 连接AD, 当△ADF为等腰三角形时,α=
第 15题图 第 16题图
16.如图,在平面直角坐标系中,O为坐标原点,将函数 y= x2- 2x(0≤ x≤ 2)的图象记为C1, 它与 x轴的交点为
O、A1。 将C1绕点A1旋转 180°得到C2, 点O的对称点为A2;将C2绕点A2旋转 180°得到C3, 点A1的对称点
为A3 , 79按此方法操作,直至得到C20. 若点P 2 ,n 在C20上,则n的值为
·第2页·
{#{QQABBDQCEsExgggCQAgAppTAAACAQA5hKCEwWGICwgKqQkBIGEgALAUQggsgOQgALAqAAoYAKIACCYAFFAABBKCAA==}#}#} }
三、解答题 (共 72分)
17.解方程 (12分) (1)2(x- 3)2= 8 (2)4x2- 6x- 3= 0
(3) (2x- 3)2= 5(2x- 3) (4) (x+ 8) (x+ 1) =-12
18. (10分)平面直角坐标系中,△ABC三个顶点分别为A(-1,4),B(-4,2),C(-3,5). (每个方格的边长均为 1个单
位长度)
(1)若△A1B1C1和△ABC关于原点O成中心对称,则C1的坐标为
(2)求出△ABC的面积。 (3)将△ABC绕点O逆时针旋转 90°,画出旋转后得到的△A2B2C2.
(4)已知点D(-2, -1), 在 x轴上找一点P, 使点P到点B与点D的距离相等,则点P的坐标为 。 (直接写
出答案)
19. (10分)如图,隧道的截面由抛物线DEC和矩形ABCD构成,矩形的长AB为 4m, 宽BC为 3m, 以DC所在
的直线为 x轴,线段CD的中垂线为 y轴,建立平面直角坐标系,y轴是抛物线的对称轴,最高点E到地面的距
离为 4m.
(1) (2) 13求出抛物线的解析式; 在距离地面 4 m高处,隧道的宽度是多少
(3)如果该隧道为单行道 (只能朝一个方向行驶),现有一辆货运卡车高 3.4m、宽 2.4m,这辆货运卡车能否通过该
隧道 通过计算说明你的结论.
·第3页·
{#{QQABDBQCEsExgggCQAgAppTAAACAQA5hKCEwWGICwgKqQkBIGEgALAUQggsgOQgALAqAAoYAKIACCYAFFAABBKCAA==}#}#} }
20. (12分)中秋期间,某商场以每盒 140元的价格购进一批月饼,当每盒月饼售价为 180元时,每天可售出 60盒.为
了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每盒月饼降价 1元,那么商场每天就可以多
售出 5盒.
(1)设售价每盒下降 x元,则每天能售出多少盒 (用含 x的代数式表示);
(2)降价多少元时,每天的销售利润w最大
(3)为保证销售利润不低于 3200元,求降价的取值范围
·第4页·
{#{QQABDBQCEsExgggCQAgAppTAAACAQA5hKCEwWGICwgKqQkBIGEgALAUQggsgOQgALAqAAoYAKIACCYAFFAABBKCAA==}#}#} }
21. (14分)
【问题背景】(1)如图 1,在四边形ABCD中,AB=AD,∠BAD= 120°,∠B=∠ADC= 90°, 点E 、F分别是边BC、
CD上的点,且∠EAF= 60°, 试探究图中线段BE、EF、FD之间的数量关系。
小王同学探究此问题的方法是:将△ABE绕A点逆时针旋转 120°得到△ADG, 连接DG. 求证:线段BE 、EF 、
FD之间的数量关系并证明。
【探索延伸】(2)如图 2,若在四边形ABCD中,4B=AD,∠B+∠D= 180°, 点E 、F分别是边BC 、CD上的点,
且∠EAF= 12 ∠BAD,上述结论是否仍然成立,并说明理由。
【学以致用】(3)如图 3,△ABC中,∠BAC= 90°,AB=AC, 点D,E均在边BC上,且∠DAE= 45°, 若BD= 1,EC
= 2, 求DE的长.
(4)如图 4,在四边形ABCD中,AD BC(BC>AD),∠B= 90°,AB=BC= 6,E是边AB上一点,当∠DCE= 45°,
BE= 2时,求DE的长度为多少
·第5页·
{#{QQABDBQCEEsxgggCQAgAppTAAACAQA5hKCEwWGICwgKqQkBIGEgALAUQggsgOQgALAqAAoYAKIACCYAFFAABBKCAA==}#}#} }
22. (14分)如图,抛物线与 x轴交于A,B两点,与 y轴交于点C,OA=OC= 6, 对称轴是 x=-2,点F在对称轴上
运动.
(1)求抛物线的解析式;
(2)是否存在一点F, 使得∠BFC为直角 若存在,求点F的坐标;若不存在,请说明理由;
(3)在直线AC上方抛物线找一点P,使△PAC面积最大,求出点P和面积最大值;
(4)将线段BC绕着点F逆时针方向旋转 90°后得到线段B1C1, 当点B1与C1恰有一点落在抛物线上时,直接写出
点F的坐标
·第6页·
{#{QQABDBQCEsExgggCQAgAppTAAACAQA5hKCEwWGICwgKqQkBIGEgALAUQggsgOQgALAqAAoYAKIACCYAFFAABBKCAA==}#}#} }
一、单选题 (共 36分)
1.下列图形中,既是轴对称图形,又是中心对称图形的是 ( )
A. B. C. D.
2. 1已知抛物线 y=- x-3 2 + 2 下列说法正确的是 ( )
A.开口向上 B.对称轴是直线 x=-3
C. 1顶点坐标为 3, 2 D.当 x<-3时,y随 x的增大而减小
3. 若 α,β是方程 x2+ 2x- 2005= 0的两个实数根,则 α2+ 3α+ β的值为 ( )
A. 2005 B. 2003 C. - 2005 D. 4010
4. 已知:2是关于 x的方程 x2- (m + 1)x +m = 0的一个实数根,并且这个方程的两个实数根恰好是等腰
△ABC的两条边的边长,则△ABC的周长为 ( )
A. 6 B. 4 C. 5 D. 4或 5
5.函数 y= ax2- x+ 2和 y=-ax- a(a≠ 0)在同一平面直角坐标系中的图象可能是 ( )
A. B. C. D.
6.如图,把图中的△ABC经过旋转变换得到△A'B'C ',如果图中△ABC上的点P的坐标为 (a,b), 那么它的对应
点P'的坐标为 ( )
A. (a- 2,b) B. (a+ 2,b) C. (-a- 2, -b) D. (a+ 2, -b)
第 6题图 第 7题图
7.如图,两个全等的等腰直角△ABC和△DEF的斜边AB=DE= 10, 点E与点A重合,斜边AB与DE在一条
直线上,△ABC保持不动,△DEF以每秒 2个单位长度的速度向右运动,直到点D与点B重合时停止运动,设
运动时间为 x秒,两个等腰直角三角形重叠部分的面积为 y个平方单位,则 y与 x函数关系的图象大致是
( )
A. B. C. D.
·第1页·
{#{QQABDBQCEEsxgggCQAgAppTAAACAQA5hKCEwWGICwgKqQkBIGEgALAUQggsgOQgALAqAAoYAKIACCYAFFAABBKCAA==}#}#} }
8.若二次函数 y= x2+ 2x+ 1在m≤ x≤m+ 1(m为常数)的范围内有最小值 1,则m的值为 ( )
A. - 3或 0 B. - 2或 1 C. - 2或 0 D. - 3≤m≤-2
9.如图,将抛物线 y= (x- 1)2的图象位于直线 y= 4以上的部分向下翻折,得到新的图象 (实线部分),若直线 y=
-x+m与新图象只有四个交点,求m的取值范围. ( )
A. 3
3
10.如图,边长为 1的正方形ABCD绕点C逆时针旋转 45°后得到正方形A'B'CD', 边A'D'与AB交于点E, 则阴
影部分的面积是 ( )
A. 2- 2 B. 2- 1 C. 2 2- 2 D. 4- 2 2
11.已知如图,在正方形ABCD中,点A、C的坐标分别是 (-1,5) (2,0),点D 1在抛物线 y= 23 x + kx的图像上,则
k的值是 ( )
A. 23 B.
1
3 C.
7
3 D.
4
3
12.已知二次函数 y= ax2+ bx+ c(a≠ 0)与 x轴的一个交点为 (4,0),其对称轴为直线 x= 1, 其部分图象如图所
示,有下列 5个结论:① abc< 0;② b2- 4ac< 0;③ 8a +c= 0;④若关于的方程 ax2+ bx+ c=-1有两个实数
根 x1,x2,且满足 x1< x2, 则 x1<-2,x2> 4;⑤直线 y= kx- 4k(k≠ 0)经过点 (0,c),则关于 x的不等式 ax2+ (b
- k)x+ c+ 4k> 0的解集是 0< x< 4. 其中正确结论的个数为 ( )
A. 5 B. 4 C. 3 D. 2
二、填空题 (共 12分)
13.若二次函数 y= ax2- 2ax+ c(a> 0)的图象经过A(-3,y1),B(4,y2),C(1,y3)三点,则 y1,y2,y3的大小关系是
14.关于 x的一元二次方程 x2- kx+ 2k- 1= 0有两个实数根分别为 x1、x2,且两个根的平方和为 7,则 k=
15.如图,∠ACB= 90°,∠BAC= 30°,将△ABC绕点C逆时针旋转 α角 (0° < α< 90°),得到△DEC. 设CD与AB
交于点F, 连接AD, 当△ADF为等腰三角形时,α=
第 15题图 第 16题图
16.如图,在平面直角坐标系中,O为坐标原点,将函数 y= x2- 2x(0≤ x≤ 2)的图象记为C1, 它与 x轴的交点为
O、A1。 将C1绕点A1旋转 180°得到C2, 点O的对称点为A2;将C2绕点A2旋转 180°得到C3, 点A1的对称点
为A3 , 79按此方法操作,直至得到C20. 若点P 2 ,n 在C20上,则n的值为
·第2页·
{#{QQABBDQCEsExgggCQAgAppTAAACAQA5hKCEwWGICwgKqQkBIGEgALAUQggsgOQgALAqAAoYAKIACCYAFFAABBKCAA==}#}#} }
三、解答题 (共 72分)
17.解方程 (12分) (1)2(x- 3)2= 8 (2)4x2- 6x- 3= 0
(3) (2x- 3)2= 5(2x- 3) (4) (x+ 8) (x+ 1) =-12
18. (10分)平面直角坐标系中,△ABC三个顶点分别为A(-1,4),B(-4,2),C(-3,5). (每个方格的边长均为 1个单
位长度)
(1)若△A1B1C1和△ABC关于原点O成中心对称,则C1的坐标为
(2)求出△ABC的面积。 (3)将△ABC绕点O逆时针旋转 90°,画出旋转后得到的△A2B2C2.
(4)已知点D(-2, -1), 在 x轴上找一点P, 使点P到点B与点D的距离相等,则点P的坐标为 。 (直接写
出答案)
19. (10分)如图,隧道的截面由抛物线DEC和矩形ABCD构成,矩形的长AB为 4m, 宽BC为 3m, 以DC所在
的直线为 x轴,线段CD的中垂线为 y轴,建立平面直角坐标系,y轴是抛物线的对称轴,最高点E到地面的距
离为 4m.
(1) (2) 13求出抛物线的解析式; 在距离地面 4 m高处,隧道的宽度是多少
(3)如果该隧道为单行道 (只能朝一个方向行驶),现有一辆货运卡车高 3.4m、宽 2.4m,这辆货运卡车能否通过该
隧道 通过计算说明你的结论.
·第3页·
{#{QQABDBQCEsExgggCQAgAppTAAACAQA5hKCEwWGICwgKqQkBIGEgALAUQggsgOQgALAqAAoYAKIACCYAFFAABBKCAA==}#}#} }
20. (12分)中秋期间,某商场以每盒 140元的价格购进一批月饼,当每盒月饼售价为 180元时,每天可售出 60盒.为
了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每盒月饼降价 1元,那么商场每天就可以多
售出 5盒.
(1)设售价每盒下降 x元,则每天能售出多少盒 (用含 x的代数式表示);
(2)降价多少元时,每天的销售利润w最大
(3)为保证销售利润不低于 3200元,求降价的取值范围
·第4页·
{#{QQABDBQCEsExgggCQAgAppTAAACAQA5hKCEwWGICwgKqQkBIGEgALAUQggsgOQgALAqAAoYAKIACCYAFFAABBKCAA==}#}#} }
21. (14分)
【问题背景】(1)如图 1,在四边形ABCD中,AB=AD,∠BAD= 120°,∠B=∠ADC= 90°, 点E 、F分别是边BC、
CD上的点,且∠EAF= 60°, 试探究图中线段BE、EF、FD之间的数量关系。
小王同学探究此问题的方法是:将△ABE绕A点逆时针旋转 120°得到△ADG, 连接DG. 求证:线段BE 、EF 、
FD之间的数量关系并证明。
【探索延伸】(2)如图 2,若在四边形ABCD中,4B=AD,∠B+∠D= 180°, 点E 、F分别是边BC 、CD上的点,
且∠EAF= 12 ∠BAD,上述结论是否仍然成立,并说明理由。
【学以致用】(3)如图 3,△ABC中,∠BAC= 90°,AB=AC, 点D,E均在边BC上,且∠DAE= 45°, 若BD= 1,EC
= 2, 求DE的长.
(4)如图 4,在四边形ABCD中,AD BC(BC>AD),∠B= 90°,AB=BC= 6,E是边AB上一点,当∠DCE= 45°,
BE= 2时,求DE的长度为多少
·第5页·
{#{QQABDBQCEEsxgggCQAgAppTAAACAQA5hKCEwWGICwgKqQkBIGEgALAUQggsgOQgALAqAAoYAKIACCYAFFAABBKCAA==}#}#} }
22. (14分)如图,抛物线与 x轴交于A,B两点,与 y轴交于点C,OA=OC= 6, 对称轴是 x=-2,点F在对称轴上
运动.
(1)求抛物线的解析式;
(2)是否存在一点F, 使得∠BFC为直角 若存在,求点F的坐标;若不存在,请说明理由;
(3)在直线AC上方抛物线找一点P,使△PAC面积最大,求出点P和面积最大值;
(4)将线段BC绕着点F逆时针方向旋转 90°后得到线段B1C1, 当点B1与C1恰有一点落在抛物线上时,直接写出
点F的坐标
·第6页·
{#{QQABDBQCEsExgggCQAgAppTAAACAQA5hKCEwWGICwgKqQkBIGEgALAUQggsgOQgALAqAAoYAKIACCYAFFAABBKCAA==}#}#} }
同课章节目录
