第12章 全等三角形 单元同步检测试题(含答案) 2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 第12章 全等三角形 单元同步检测试题(含答案) 2024—2025学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 571.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-09 18:04:08 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十二章《全等三角形》单元检测题
一、选择题(每题3分,共30分)
1. 下列汽车标志中,不是由多个全等图形组成的是( )
A. B. C. D.
2如图,红红书上的三角形被墨迹污染了一部分,她根据所学的知识很快就画了一个与书上完全一样的三角形,那么红红画图的依据是( )
A.SSS B.SAS C.ASA D.AAS
3如图,Rt△ABC中,AD是∠BAC的平分线,DE⊥AB,垂足为E.若AB=10cm,AC=6cm,则BE的长度为( )
A.10cm B.6cm C.4cm D.2cm
4如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的( )
A.AB=CD B.EC=BF C.∠A=∠D D.AB=BC
5.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,若BF=AC,∠CAD=25°,则∠ABE的度数为( )
A.30° B.15° C.25° D.20°
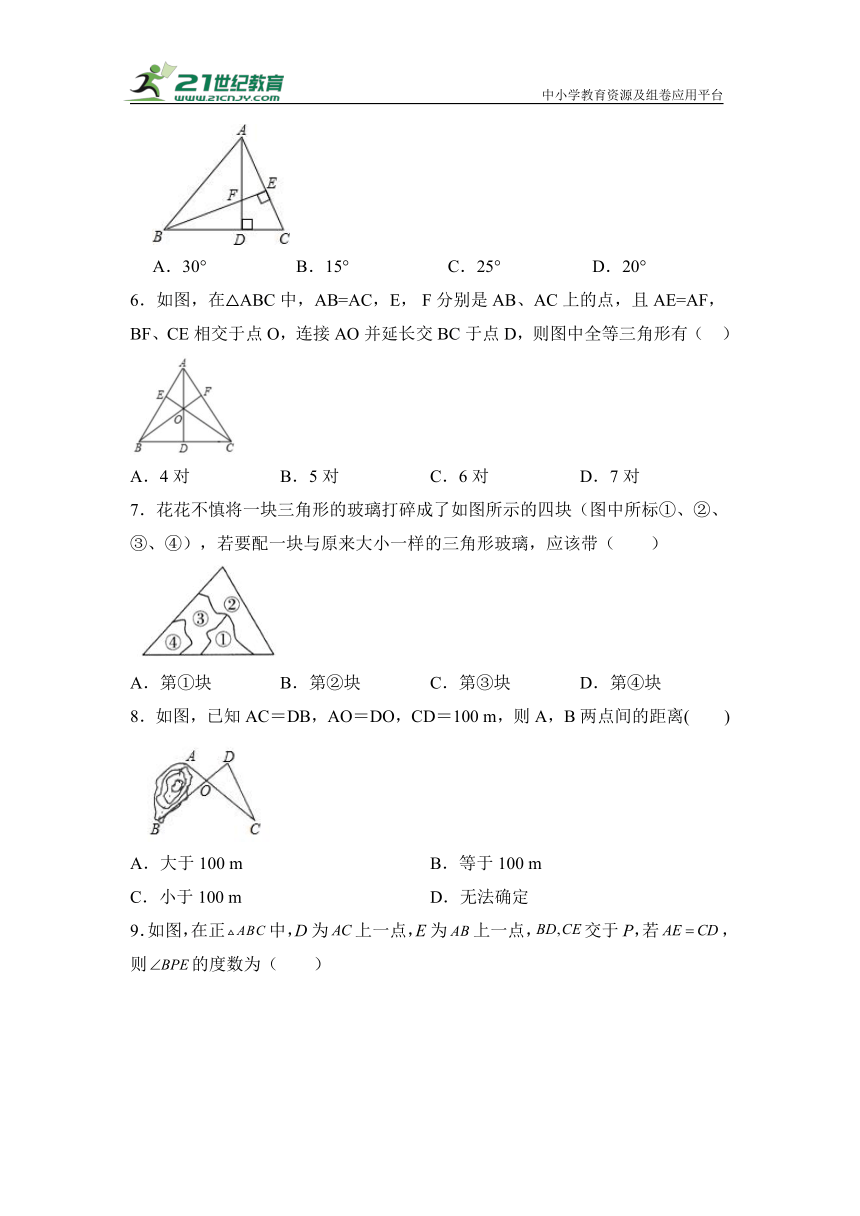
6.如图,在△ABC中,AB=AC,E, F分别是AB、AC上的点,且AE=AF,BF、CE相交于点O,连接AO并延长交BC于点D,则图中全等三角形有( )
A.4对 B.5对 C.6对 D.7对
7.花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①、②、③、④),若要配一块与原来大小一样的三角形玻璃,应该带( )
A.第①块 B.第②块 C.第③块 D.第④块
8.如图,已知AC=DB,AO=DO,CD=100 m,则A,B两点间的距离( )
A.大于100 m B.等于100 m
C.小于100 m D.无法确定
9.如图,在正中,D为上一点,E为上一点,交于P,若,则的度数为( )
A. B. C. D.
10.已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC②∠BCE+∠BCD=180°③AD=AE=EC ④ BA+BC=2BF其中正确的是( )
A.①②③ B.①③④ C.①②④ D.①②③④
二、填空题(每题3分,共24分)
11.已知图中的两个三角形全等,则的大小为_______.
12.如图所示,在平面坐标系中,,,则点A的坐标是_____.
13.如图,在中,为中线,且,则边的取值范围是___________.
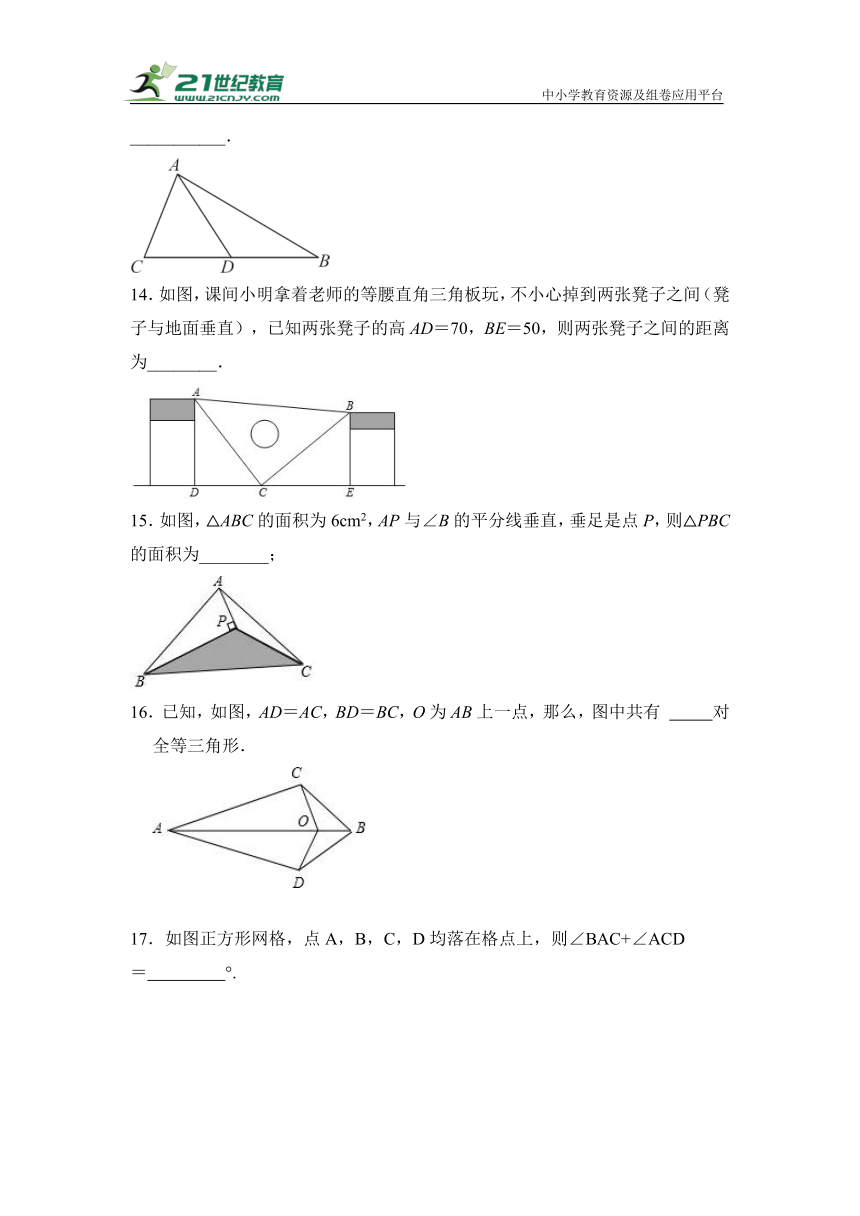
14.如图,课间小明拿着老师的等腰直角三角板玩,不小心掉到两张凳子之间(凳子与地面垂直),已知两张凳子的高AD=70,BE=50,则两张凳子之间的距离为________.
15.如图,△ABC的面积为6cm2,AP与∠B的平分线垂直,垂足是点P,则△PBC的面积为________;
16.已知,如图,AD=AC,BD=BC,O为AB上一点,那么,图中共有 对全等三角形.
17.如图正方形网格,点A,B,C,D均落在格点上,则∠BAC+∠ACD= °.
18.如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作MN∥BC,分别交A
B、AC于点M,N.若AB=8,AC=10,则△AMN的周长是 .
三.解答题(共46分,19题6分,20 ---24题8分)
19. (6分)已知:如图,AB=CD,BE=DF,AE=CF. 求证:EO=FO.
20. (6分)如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC. 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
21.(6分)如图,点D、E分别是AB、AC的中点,BE、CD相交于点O,∠B=∠C,BD=CE.求证:
(1)OD=OE;
(2)△ABE≌△ACD.
22.(6分)如图,在四边形中,,为的中点,连接、,,延长交的延长线于点.
(1)求证:;
(2)若,,求四边形的面积.
23.如图,,,,,垂足为.
(1)求证:;
(2)求的度数;
(3)求证:.
24.如图,已知中,,,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,与是否全等,请说明理由.
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使与全等.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿三边运动,求经过多长时间点P与点Q第一次在的哪条边上相遇.
答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C A C D B B B C
二、填空题
11.
12..
13.
14.120
解:由题意可得:∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
则∠DAC=∠BCE,
在△ACD和△CBE中,
∴△ACD≌△CBE(AAS),
∴DC=BE=50,AD=CE=70,
则两张凳子之间的距离为:50+70=120.
故答案为:120.
15.3cm2
16.解:∵AD=AC,BD=BC,AB=AB,
∴△ADB≌△ACB;
∴∠CAO=∠DAO,∠CBO=∠DBO,
∵AD=AC,BD=BC,OA=OA,OB=OB
∴△ACO≌△ADO,△CBO≌△DBO.
∴图中共有3对全等三角形.
故答案为:3.
17.【答案】90
【解析】【解答】解:在△DCE和△ABD中,
,
∴△DCE≌△ABD(SAS),
∴∠CDE=∠DAB,
∵∠CDE+∠ADC=∠ADC+∠DAB=90°,
∴∠AFD=90°,
∴∠BAC+∠ACD=90°.
故答案为:90.
【分析】设AB与CD交于点F,易证△DCE≌△ABD,得到∠CDE=∠DAB,推出∠AFD=90°,然后结合外角的性质进行解答.
18.【答案】18
三、解答题
19. 证明:在△ABE和△CDF中,AB=CD,BE=DF,AE=CF,
∴△ABE≌△CDF(SSS),∴∠AEB=∠CFD,∴∠AEO=∠CFO.
在△AOE和△COF中,∠AOE=∠COF,∠AEO=∠CFO,AE=CF,
∴△AOE≌△COF(AAS),∴EO=FO.
20. 猜想:BE=EC,BE⊥EC.
∵△AED是直角三角形,∴∠AED=90°,且有一个锐角是45°,
∴∠EAD=∠EDA=45°,∴AE=DE,
∵∠BAC=90°,
∴∠EAB=∠EAD+∠BAC=45°+90°=135°,∠EDC=∠ADC-∠EDA=180°-45°=135°,∴∠EAB=∠EDC,
∵D是AC的中点,∴AD= AC,
∵AC=2AB,∴AB=AD=DC,
∵在△EAB和△EDC中,AE=DE,∠EAB=∠EDC,AB=DC,
∴△EAB≌△EDC(SAS),
∴EB=EC,且∠AEB=∠DEC,
∴∠BEC=∠DEC+∠BED=∠AEB+∠BED=∠AED=90°,∴BE⊥EC.
21.(1)证明见解析;(2)证明见解析.
解:(1)∵∠B=∠C,∠DOB=∠EOC,BD=CE
∴△DOB≌△EOC(AAS)
∴OD=OE;
(2)∵D、E分别是AB、AC的中点
∴AB=2BD,AC=2CE,AD=BD,AE=EC
又∵BD=CE
∴AB=AC,AD=AE
∵∠A=∠A
∴△ABE≌△ACD(SAS)
22.(1)见解析;(2)
解:(1)∵AD∥BC,
∴∠ADE=∠FCE,
∵∠AED=∠FEC,DE=CE,
∴△AED≌△FEC,
∴FC=AD;
(2)∵△AED≌△FEC,
∴,AE=EF,
∴,
∴==
==.
23.(1)证明见解析;(2)135°;(3)证明见解析
【详解】
证明:(1),
,,
,
在和中,
,
;
(2),,
,
由(1)知,
,
,
,
,
;
(3)延长到,使得,
,
,
在和中,
,
,
,,
,
,,,
,,
,
,
在和中,
,
,
,
,
.
24.(1)①,理由见解析;②;(2)经过点P与点Q第一次在边AB上相遇
【详解】
解:(1)①∵,
∴,
∵,点为的中点,
∴.
又∵,,
∴,∴.
又∵,∴,
在和中,
,
∴.
②∵,
∴
若,,
则,,
∴点P,点Q运动的时间,
∴.
(2)设经过秒后点P与点Q第一次相遇,
由题意,得,
解得.
∴点P共运动了.
周长为:,
若是运动了三圈即为:,
∵的长度,
∵点P、点Q在AB边上相遇,
∴经过点P与点Q第一次在边AB上相遇.
www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
第十二章《全等三角形》单元检测题
一、选择题(每题3分,共30分)
1. 下列汽车标志中,不是由多个全等图形组成的是( )
A. B. C. D.
2如图,红红书上的三角形被墨迹污染了一部分,她根据所学的知识很快就画了一个与书上完全一样的三角形,那么红红画图的依据是( )
A.SSS B.SAS C.ASA D.AAS
3如图,Rt△ABC中,AD是∠BAC的平分线,DE⊥AB,垂足为E.若AB=10cm,AC=6cm,则BE的长度为( )
A.10cm B.6cm C.4cm D.2cm
4如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的( )
A.AB=CD B.EC=BF C.∠A=∠D D.AB=BC
5.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,若BF=AC,∠CAD=25°,则∠ABE的度数为( )
A.30° B.15° C.25° D.20°
6.如图,在△ABC中,AB=AC,E, F分别是AB、AC上的点,且AE=AF,BF、CE相交于点O,连接AO并延长交BC于点D,则图中全等三角形有( )
A.4对 B.5对 C.6对 D.7对
7.花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①、②、③、④),若要配一块与原来大小一样的三角形玻璃,应该带( )
A.第①块 B.第②块 C.第③块 D.第④块
8.如图,已知AC=DB,AO=DO,CD=100 m,则A,B两点间的距离( )
A.大于100 m B.等于100 m
C.小于100 m D.无法确定
9.如图,在正中,D为上一点,E为上一点,交于P,若,则的度数为( )
A. B. C. D.
10.已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC②∠BCE+∠BCD=180°③AD=AE=EC ④ BA+BC=2BF其中正确的是( )
A.①②③ B.①③④ C.①②④ D.①②③④
二、填空题(每题3分,共24分)
11.已知图中的两个三角形全等,则的大小为_______.
12.如图所示,在平面坐标系中,,,则点A的坐标是_____.
13.如图,在中,为中线,且,则边的取值范围是___________.
14.如图,课间小明拿着老师的等腰直角三角板玩,不小心掉到两张凳子之间(凳子与地面垂直),已知两张凳子的高AD=70,BE=50,则两张凳子之间的距离为________.
15.如图,△ABC的面积为6cm2,AP与∠B的平分线垂直,垂足是点P,则△PBC的面积为________;
16.已知,如图,AD=AC,BD=BC,O为AB上一点,那么,图中共有 对全等三角形.
17.如图正方形网格,点A,B,C,D均落在格点上,则∠BAC+∠ACD= °.
18.如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作MN∥BC,分别交A
B、AC于点M,N.若AB=8,AC=10,则△AMN的周长是 .
三.解答题(共46分,19题6分,20 ---24题8分)
19. (6分)已知:如图,AB=CD,BE=DF,AE=CF. 求证:EO=FO.
20. (6分)如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC. 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
21.(6分)如图,点D、E分别是AB、AC的中点,BE、CD相交于点O,∠B=∠C,BD=CE.求证:
(1)OD=OE;
(2)△ABE≌△ACD.
22.(6分)如图,在四边形中,,为的中点,连接、,,延长交的延长线于点.
(1)求证:;
(2)若,,求四边形的面积.
23.如图,,,,,垂足为.
(1)求证:;
(2)求的度数;
(3)求证:.
24.如图,已知中,,,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,与是否全等,请说明理由.
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使与全等.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿三边运动,求经过多长时间点P与点Q第一次在的哪条边上相遇.
答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C A C D B B B C
二、填空题
11.
12..
13.
14.120
解:由题意可得:∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
则∠DAC=∠BCE,
在△ACD和△CBE中,
∴△ACD≌△CBE(AAS),
∴DC=BE=50,AD=CE=70,
则两张凳子之间的距离为:50+70=120.
故答案为:120.
15.3cm2
16.解:∵AD=AC,BD=BC,AB=AB,
∴△ADB≌△ACB;
∴∠CAO=∠DAO,∠CBO=∠DBO,
∵AD=AC,BD=BC,OA=OA,OB=OB
∴△ACO≌△ADO,△CBO≌△DBO.
∴图中共有3对全等三角形.
故答案为:3.
17.【答案】90
【解析】【解答】解:在△DCE和△ABD中,
,
∴△DCE≌△ABD(SAS),
∴∠CDE=∠DAB,
∵∠CDE+∠ADC=∠ADC+∠DAB=90°,
∴∠AFD=90°,
∴∠BAC+∠ACD=90°.
故答案为:90.
【分析】设AB与CD交于点F,易证△DCE≌△ABD,得到∠CDE=∠DAB,推出∠AFD=90°,然后结合外角的性质进行解答.
18.【答案】18
三、解答题
19. 证明:在△ABE和△CDF中,AB=CD,BE=DF,AE=CF,
∴△ABE≌△CDF(SSS),∴∠AEB=∠CFD,∴∠AEO=∠CFO.
在△AOE和△COF中,∠AOE=∠COF,∠AEO=∠CFO,AE=CF,
∴△AOE≌△COF(AAS),∴EO=FO.
20. 猜想:BE=EC,BE⊥EC.
∵△AED是直角三角形,∴∠AED=90°,且有一个锐角是45°,
∴∠EAD=∠EDA=45°,∴AE=DE,
∵∠BAC=90°,
∴∠EAB=∠EAD+∠BAC=45°+90°=135°,∠EDC=∠ADC-∠EDA=180°-45°=135°,∴∠EAB=∠EDC,
∵D是AC的中点,∴AD= AC,
∵AC=2AB,∴AB=AD=DC,
∵在△EAB和△EDC中,AE=DE,∠EAB=∠EDC,AB=DC,
∴△EAB≌△EDC(SAS),
∴EB=EC,且∠AEB=∠DEC,
∴∠BEC=∠DEC+∠BED=∠AEB+∠BED=∠AED=90°,∴BE⊥EC.
21.(1)证明见解析;(2)证明见解析.
解:(1)∵∠B=∠C,∠DOB=∠EOC,BD=CE
∴△DOB≌△EOC(AAS)
∴OD=OE;
(2)∵D、E分别是AB、AC的中点
∴AB=2BD,AC=2CE,AD=BD,AE=EC
又∵BD=CE
∴AB=AC,AD=AE
∵∠A=∠A
∴△ABE≌△ACD(SAS)
22.(1)见解析;(2)
解:(1)∵AD∥BC,
∴∠ADE=∠FCE,
∵∠AED=∠FEC,DE=CE,
∴△AED≌△FEC,
∴FC=AD;
(2)∵△AED≌△FEC,
∴,AE=EF,
∴,
∴==
==.
23.(1)证明见解析;(2)135°;(3)证明见解析
【详解】
证明:(1),
,,
,
在和中,
,
;
(2),,
,
由(1)知,
,
,
,
,
;
(3)延长到,使得,
,
,
在和中,
,
,
,,
,
,,,
,,
,
,
在和中,
,
,
,
,
.
24.(1)①,理由见解析;②;(2)经过点P与点Q第一次在边AB上相遇
【详解】
解:(1)①∵,
∴,
∵,点为的中点,
∴.
又∵,,
∴,∴.
又∵,∴,
在和中,
,
∴.
②∵,
∴
若,,
则,,
∴点P,点Q运动的时间,
∴.
(2)设经过秒后点P与点Q第一次相遇,
由题意,得,
解得.
∴点P共运动了.
周长为:,
若是运动了三圈即为:,
∵的长度,
∵点P、点Q在AB边上相遇,
∴经过点P与点Q第一次在边AB上相遇.
www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
