22.3实际问题与二次函数同步练习(含解析)
文档属性
| 名称 | 22.3实际问题与二次函数同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 808.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-09 00:00:00 | ||
图片预览



文档简介
22.3 实际问题与二次函数 同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某企业是一家专门生产季节性产品的企业,当产品无利润时,企业会自动停产,经过调研预测,它一年中每月获得的利润(万元)和月份之间满足函数关系式,则企业停产的月份为( )
A.2月和12月 B.2月至12月 C.1月 D.1月、2月和12月
2.使用家用燃气灶烧开同一壶水所需的燃气量(单位:)与旋钮的旋转角度(单位:度)()近似满足函数关系.如图记录了某种家用燃气灶烧开同壶水的旋钮角度与燃气量的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开壶水最节省燃气的旋钮角度约为( )
A.37.5° B.40° C.52.5° D.55°
3.一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式:h=-5(t-1)2+6,则小球距离地面的最大高度是( )
A.1米 B.5米 C.6米 D.7米
4.在西宁市中考体考前,某初三学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间满足函数解析式yx2x,由此可知该生此次实心球训练的成绩为( )
A.6米 B.8米 C.10米 D.12米
5.用16米长的围栏围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,小红提出了围成半圆形、矩形、等腰三角形(底边靠墙)这三种方案(如图),最佳方案是( )
A.方案一 B.方案二 C.方案三 D.三种方案都一样
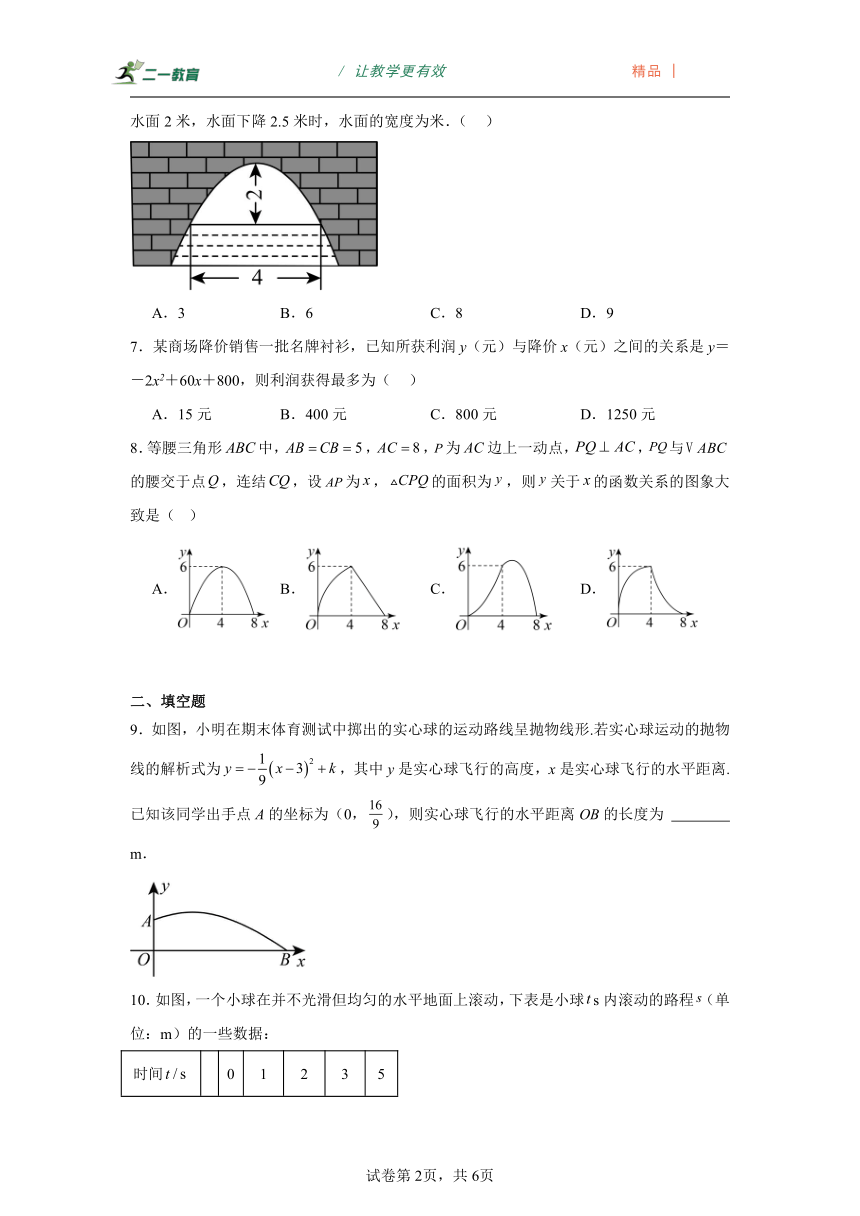
6.如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降2.5米时,水面的宽度为米.( )
A.3 B.6 C.8 D.9
7.某商场降价销售一批名牌衬衫,已知所获利润y(元)与降价x(元)之间的关系是y=-2x2+60x+800,则利润获得最多为( )
A.15元 B.400元 C.800元 D.1250元
8.等腰三角形中,,,为边上一动点,,与的腰交于点,连结,设为,的面积为,则关于的函数关系的图象大致是( )
A. B. C. D.
二、填空题
9.如图,小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为(0,),则实心球飞行的水平距离OB的长度为 m.
10.如图,一个小球在并不光滑但均匀的水平地面上滚动,下表是小球s内滚动的路程(单位:m)的一些数据:
时间 0 1 2 3 5
路程 0 10
已知是关于的二次函数,则当时,的值为 .
11.如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度为 米.
12.月日晚时,南昌以天空为幕,以烟花为笔,举办了一场盛大的“风景这边独好”——南昌市国庆烟花晚会,热烈庆祝伟大祖国岁生日.其中,一种新型礼炮的升空高与飞行时间的关系式是,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要时间为 .
13.如图,P是抛物线y=x2﹣x﹣4在第四象限的一点,过点P分别向x轴和y轴作垂线,垂足分别为A、B,则四边形OAPB周长的最大值为 .
三、解答题
14.如图,要建一个圆形喷水池,在池中心竖直安置一根水管,在水管的顶端A安一个喷水头,使喷出的抛物线形水柱与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m.以水管与地面的交点为原点,原点与水柱落地处所在直线为x轴,水管所在直线为y轴,建立平面直角坐标系,每个单位长度表示1m.
(1)求水管的长度.
(2)如图2,是图中抛物线上一动点,点与点P关于y轴对称,画出点所在的抛物线的草图,并直接写出点所在抛物线的解析式及自变量的取值范围.
(3)将水管OA喷水头往上平移m,求水柱落地处离池中心的距离.
15.掷实心球是中考体育项目之一,为了在体育中考中取得更好的成绩,小鹏积极训练,如图所示,实心球经过的路线是一条抛物线,掷出时,实心球出手处距离地面的高度是2,实心球的落地点为处,以为原点,所在直线为轴,所在直线为轴建立平面直角坐标系,当实心球运行的水平距离为3时,达到最大高度3的处.
(1)求抛物线的解析式;
(2)若成绩想要达到80分,实心球出手处至球落地处的水平距离至少为8.4,小鹏此次投掷的成绩能上80分吗?
16.如图,已知抛物线y=x2-(k+1)x+1的顶点A在x轴的负半轴上,且与一次函数y=-x+1交于点B和点C
(1)求k的值;
(2)求ABC的面积.
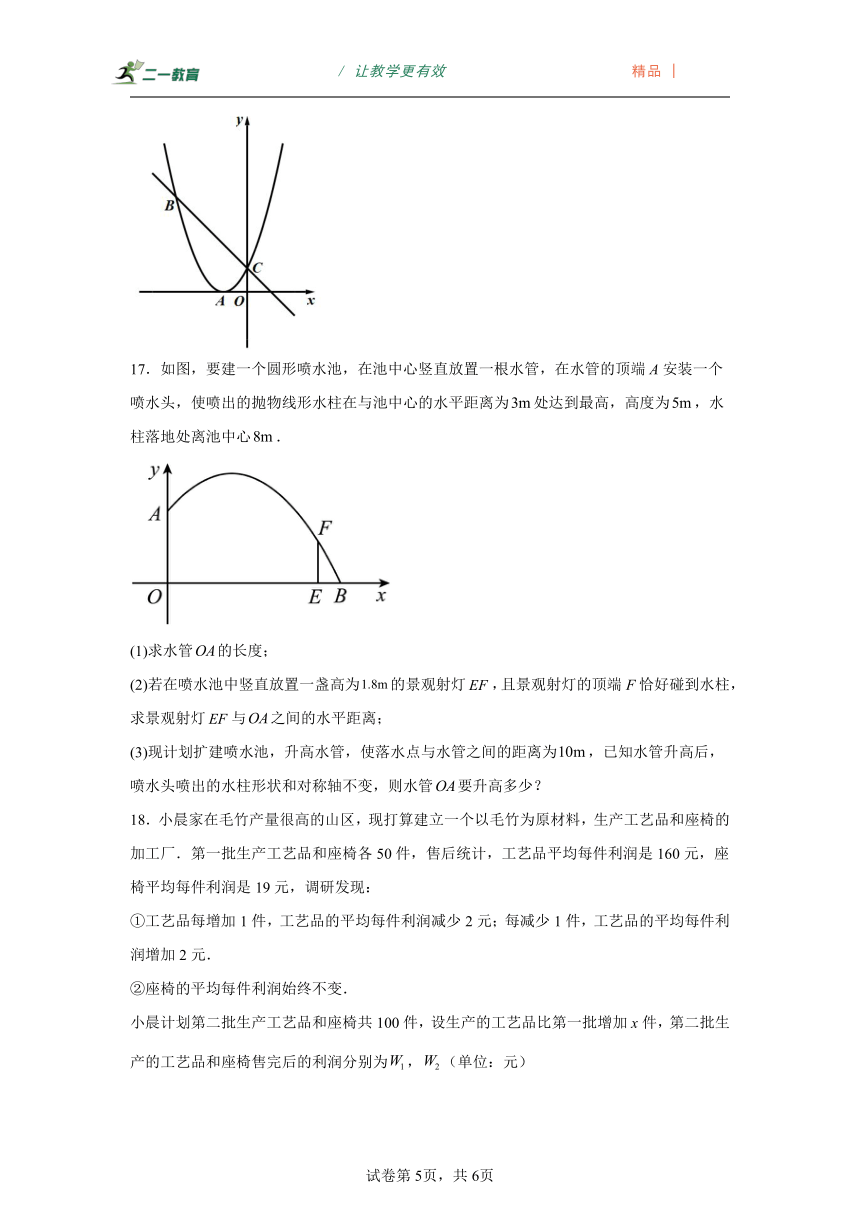
17.如图,要建一个圆形喷水池,在池中心竖直放置一根水管,在水管的顶端A安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为,水柱落地处离池中心.
(1)求水管的长度;
(2)若在喷水池中竖直放置一盏高为的景观射灯,且景观射灯的顶端F恰好碰到水柱,求景观射灯与之间的水平距离;
(3)现计划扩建喷水池,升高水管,使落水点与水管之间的距离为,已知水管升高后,喷水头喷出的水柱形状和对称轴不变,则水管要升高多少?
18.小晨家在毛竹产量很高的山区,现打算建立一个以毛竹为原材料,生产工艺品和座椅的加工厂.第一批生产工艺品和座椅各50件,售后统计,工艺品平均每件利润是160元,座椅平均每件利润是19元,调研发现:
①工艺品每增加1件,工艺品的平均每件利润减少2元;每减少1件,工艺品的平均每件利润增加2元.
②座椅的平均每件利润始终不变.
小晨计划第二批生产工艺品和座椅共100件,设生产的工艺品比第一批增加x件,第二批生产的工艺品和座椅售完后的利润分别为,(单位:元)
(1)用含x的代数式分别表示,;
(2)当x取何值时,第二批生产的工艺品和座椅售完后获得的总利润W最大,最大总利润是多少?
19.一名身高为1.8m的篮球运动员甲在距篮筐(点B)水平距离4m处跳起投篮,篮球准确落入篮筐,已知篮球的运动路线是抛物线,篮球在运动员甲头顶上方0.25m处(点A)出手,篮球在距离篮筐水平距离为1.5m处达到最大高度3.5m,以水平地面为x轴,篮球达到最大高度时的铅直方向为y轴,建立如图所示的平面直角坐标系.
(1)求篮球运动路线(抛物线)的函数解析式;
(2)求篮球出手时,运动员甲跳离地面的高度是多少米?
(3)已知运动员乙跳离地面时,最高能摸到3.3运动员乙在运动员甲与篮筐之间的什么范围内能在空中截住球?
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】求出时的月份,以及时的月份,即可.
【详解】解:∵,
∴当时,,
解得:;
又当时,;
∴企业停产的月份为1月、2月和12月;
故选D.
【点睛】本题考查二次函数的实际应用.理解题意,正确的求出自变量的值,是解题的关键.
2.B
【分析】根据题意和二次函数的性质,可以确定出对称x的取值范围,从而可以解答本题.
【详解】解:由图象可得,
该函数的对称轴x>且x<50,
∴37.5<x<50,
∴此燃气灶烧开壶水最节省燃气的旋钮角度约为40°,
故选:B.
【点睛】本题考查二次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
3.C
【详解】试题解析:∵高度h和飞行时间t 满足函数关系式:h=-5(t-1)2+6,
∴当t=1时,小球距离地面高度最大,
∴h=-5×(1-1)2+6=6米,
故选C.
考点:二次函数的应用.
4.C
【分析】根据铅球落地时,高度y=0,把实际问题可理解为当y=0时,求x的值即可.
【详解】解:当y=0时,即yx2x0,
解得:x=﹣2(舍去),x=10.
∴该生此次实心球训练的成绩为10米.
故选:C.
【点睛】本题考查了二次函数的应用中函数式中变量与函数表达的实际意义,需要结合题意,取函数或自变量的特殊值列方程求解是解题关键.
5.A
【分析】先分别算出各种方案中图形的面积,再比较大小求解.
【详解】解:设围成的图形的面积为平方米,
方案一:设圆的半径为米,则:,
解得:,
(平方米);
方案二:设与墙相邻的边长为米,则另一边为米,
由题意得:,
,
当时,有最大值,最大值为32平方米;
方案三:围栏的长为16米,
等腰三角形的腰为8米,
当顶角为直角时,面积最大,此时(平方米);
,
∴最佳方案是方案一;
故选A
【点睛】本题考查了二次函数的应用,计算图形的面积是解题的关键.
6.B
【分析】本题主要考查了二次函数的应用,根据已知建立直角坐标系,进而求出二次函数解析式,再通过把代入抛物线解析式求出水面宽度即可,根据已知建立坐标系从而得出二次函数解析式是解决问题的关键.
【详解】解:建立平面直角坐标系,设横轴通过,纵轴轴通过中点且通过点,则通过画图可得为原点,抛物线以轴为对称轴,且经过、两点,和可求出为的一半为米,抛物线的顶点坐标为,
,
设顶点式为,代入点的坐标,
得出,
解得:,
抛物线的解析式为:,
当水面下降2.5米时,即当时,,
解得:,
水面的宽度为(米),
故选:B.
7.D
【分析】将函数关系式转化为顶点式,然后利用开口方向和顶点坐标即可求出最多的利润.
【详解】解:y=-2x2+60x+800=-2(x-15)2+1250
∵-2<0
故当x=15时,y有最大值,最大值为1250
即利润获得最多为1250元
故选:D.
【点睛】此题考查的是利用二次函数求最值,掌握将二次函数的一般式转化为顶点式求最值是解决此题的关键.
8.D
【分析】过B作BD⊥AC于D,则AD=CD=4,由勾股定理可得BD=3,再分两种情况进行讨论:当Q在AB上时,求得△CPQ面积y=PQ×CP=-x2+3x(0≤x<4);当Q在BC上时,求得△CPQ面积y=PQ×CP=x2-6x+24(4≤x≤8),据此判断函数图象即可.
【详解】解:过作于,则,
∴由勾股定理可得,,
如图所示,当在上时,
由,可得,
∴,
又∵,
∴面积;
如图所示,当在上时,,
由,可得,
∴面积,
∴当时,函数图象是开口向下的抛物线;当时,函数图象是开口向上的抛物线.
故选:D.
【点睛】本题主要考查了动点问题的函数图象,解题时注意:二次函数的图象为抛物线,开口方向由二次项的系数符号决定,用图象解决问题时,要理清图象的含义即会识图.
9.8
【分析】根据出手点A的坐标为(0,),求出函数关系式,再令y=0可解得答案.
【详解】解:把A(0,)代入得:
,
∴,
∴,
令y=0得,
解得x=2(舍去)或x=8,
∴实心球飞行的水平距离OB的长度为8m,
故答案为:8.
【点睛】本题考查二次函数的应用,解题的关键是理解题意,能用待定系数法求出函数关系式.
10.
【分析】本题考查了二次函数的应用.利用待定系数法得到函数解析式,再将代入计算即可得到答案.
【详解】解:设二次函数的解析式为,
将,代入得,
解得,
∴二次函数的解析式为,
当时,,
故答案为:
11.
【分析】根据已知得出直角坐标系,进而求出二次函数解析式,再通过把代入抛物线解析式得出水面宽度,即可得出答案.
【详解】解:建立平面直角坐标系,设横轴x通过,纵轴y通过中点O且通过C点,如图,
抛物线以y轴为对称轴,且经过A,B两点,和可求出为的一半,为2米,抛物线顶点C坐标为,点A坐标为,
通过以上条件可设顶点式,
代入A点坐标,可得,
解得:,所以抛物线解析式为,
当水面下降1米,通过抛物线在图上的观察可转化为:
当时,对应的抛物线上两点之间的距离,也就是直线与抛物线相交的两点之间的距离,
可以通过把代入抛物线解析式得出:
,解得:,
所以水面宽度为米,
故答案为:.
【点睛】此题主要考查了二次函数的应用,根据已知建立坐标系从而得出二次函数解析式是解决问题的关键.
12./4秒
【分析】把二次函数写成顶点式,顶点为礼炮点火升空到最高点处的位置,则顶点的横坐标即为所求.
【详解】∵,
∵ ,
∴当时,函数有最大值,为,
∴.这种礼炮点火升空到最高点处引爆,则从点火升空到引爆需要的时间为,
故答案为:.
【点睛】此题考查了二次函数在实际问题中的应用,熟练掌握二次函数的性质是解题的关键.
13.10
【分析】设P(x,x2﹣x﹣4)根据矩形的周长公式得到C=﹣2(x﹣1)2+10.根据二次函数的性质来求最值即可.
【详解】解:设P(x,x2﹣x﹣4),
四边形OAPB周长=2PA+2OA=﹣2(x2﹣x﹣4)+2x=﹣2x2+4x+8=﹣2(x﹣1)2+10,
当x=1时,四边形OAPB周长有最大值,最大值为10.
故答案为10.
【点睛】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的性质.
14.(1)
(2)图像如图所示,
(3)
【分析】对于(1),根据题意可知图象的顶点坐标为,经过点,再设顶点式并求出,令可得答案;
对于(2),先画出图象,再确定点的坐标,进而得出关系式,并求出自变量取值范围;
对于(3),先求出平移后的关系式,再令,可得答案.
【详解】(1)根据题意可知图象的顶点坐标为,经过点.
设二次函数的关系式为,根据题意,得
.
又∵图象经过点,
∴,
解得,
∴二次函数的关系式为.
当时,,
∴m.
(2)如图所示.
由(1),得二次函数的关系式为.
则点关于y轴对称的点的坐标为,
∴点所在抛物线的关系式为();
(3)将水管喷头往上平移,可得关系式为.
令,得,
解得或(舍).
所以水柱落地后离中心的距离是.
【点睛】本题主要考查了待定系数法求二次函数关系式,画二次函数图像,二次函数图像的平移,二次函数的对称性等,选择适当的关系式是解题的关键.
15.(1)
(2)不能
【分析】本题主要考查了二次函数的应用、解一元二次方程、实数比较大小等知识,正确解得该抛物线解析式是解题关键.
(1)根据题意,设该抛物线解析式为,然后将将点代入求解即可;
(2)对于抛物线,令,解得的值,进而确定点坐标,根据题意比较点横坐标与8.4的大小,即可获得答案.
【详解】(1)解:根据题意,可得,该抛物线顶点坐标为,
设该抛物线解析式为,
将点代入,可得,
解得,
∴该抛物线解析式为;
(2)对于抛物线,
令,可得,
整理可得,
解得,,
∵点在轴正半轴上,
∴,
又∵,
∴小鹏此次投掷的成绩不能上80分.
16.(1)k=-3;(2)3
【分析】(1)根据抛物线顶点A在x轴的负半轴上,得到△=0,故可求出m;
(2)求出A,B,C坐标,根据割补法即可求解.
【详解】(1)依题意可得[-(k+1)] 2-4=0
解得k=1或k=-3
∵顶点A在x轴的负半轴上,
∴-(k+1)>0
即k<-1
∴k=-3
∴y=x2+2x+1=(x+1)2,故A(-1,0)
(2)令一次函数x=0,代入y=-x+1=1
∴C(0,1)
联立
解得或
∴B(-3,4)
∴S△ABC=3×4-×3×3-×4×2-×1×1=3.
【点睛】此题主要考查二次函数的图象与几何综合,解题的关键是熟知二次函数的图象与性质.
17.(1)水管的长度为
(2)景观射灯与之间的水平距离为
(3)水管要升高
【分析】该题考查了二次函数的应用,此类问题一般涉及抛球、投篮、隧道、拱桥、喷泉水柱等.解决此类问题的关键是理解题目中的条件所表示的几何意义.
(1)用待定系数法求出抛物线的表达式,令,即可求解;
(2)把代入解析式,即可求解;
(3)设水管要升高,求出扩建后抛物线的表达式,即可求解;
【详解】(1)解:由题意可知,,
设抛物线的表达式为,
∵点在抛物线上,
∴,
解得,
∴抛物线的表达式为.
令,得,
∴水管的长度为.
(2)把代入得,
解得(舍去),
∴景观射灯与之间的水平距离为;
(3)设水管要升高,
则扩建后抛物线的表达式为,
把代入得,
解得,
∴水管要升高.
18.(1),;(2)当时,第二批生产的工艺品和座椅售完后获得的总利润W最大,最大总利润是9160元
【分析】(1)设第二批生产的工艺品比第一批增加x件,则工艺品有件,座椅有件,根据“利润=件数每件的利润”可得函数解析式;
(2)将工艺品的利润加上座椅的利润可得总利润关于x的函数解析式,配方成顶点式,利用二次函数的性质求解可得.
【详解】解:设第二批生产的工艺品比第一批增加x件,则工艺品有件,座椅有件,
由题意得:,
;
根据题意,得:
,
,
,
,
∵,且x为整数,
当时,W取得最大值,最大值为9160,
答:当时,第二批生产的工艺品和座椅售完后获得的总利润W最大,最大总利润是9160元.
【点睛】本题主要考查二次函数的应用,解题的关键是理解题意,找到题目蕴含的相等关系,据此列出函数解析式及二次函数的性质.
19.(1)
(2)0.2米
(3)乙在运动员距离甲1.5米之内以及篮板0.5米之内能在空中截住球.
【分析】(1)设抛物线的表达式为,依题意可知图象经过的坐标,由此可得a的值即可;
(2)当x=-2.5时,y=-0.2×(-2.5)2+3.5=2.25,即可得到结论.
(3)当y=3.3代入函数解析式,求出x的值,即可得出答案.
【详解】(1)∵抛物线的顶点坐标为(0,3.5),
∴设抛物线的解析式为.
由题意可知,抛物线上的点的坐标为(1.5,3.05).
∴,
解得,
∴抛物线的解析式为;
(2)设篮球出手时,运动员甲跳离地面的高度为.
4-1.5=2.5,0.25+1.8=2.05.
由题意可得点A的坐标为,
∴,
∴.
∴篮球出手时,运动员跳离地面的高度是0.2米;
(3)由题意可得出:y=3.3,
则3.3=-0.2x2+3.5
解得:x1=1,x2=-1,
∴1.5-1=0.5,-2.5-(-1)=1.5,
∴乙在运动员距离甲1.5米之内以及篮板0.5米之内能在空中截住球.
【点睛】此题主要考查了二次函数的应用;建立合适的平面直角坐标系是解决本题的突破点;求得球出手时距离地面的高度是解决本题的关键.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某企业是一家专门生产季节性产品的企业,当产品无利润时,企业会自动停产,经过调研预测,它一年中每月获得的利润(万元)和月份之间满足函数关系式,则企业停产的月份为( )
A.2月和12月 B.2月至12月 C.1月 D.1月、2月和12月
2.使用家用燃气灶烧开同一壶水所需的燃气量(单位:)与旋钮的旋转角度(单位:度)()近似满足函数关系.如图记录了某种家用燃气灶烧开同壶水的旋钮角度与燃气量的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开壶水最节省燃气的旋钮角度约为( )
A.37.5° B.40° C.52.5° D.55°
3.一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式:h=-5(t-1)2+6,则小球距离地面的最大高度是( )
A.1米 B.5米 C.6米 D.7米
4.在西宁市中考体考前,某初三学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间满足函数解析式yx2x,由此可知该生此次实心球训练的成绩为( )
A.6米 B.8米 C.10米 D.12米
5.用16米长的围栏围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,小红提出了围成半圆形、矩形、等腰三角形(底边靠墙)这三种方案(如图),最佳方案是( )
A.方案一 B.方案二 C.方案三 D.三种方案都一样
6.如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降2.5米时,水面的宽度为米.( )
A.3 B.6 C.8 D.9
7.某商场降价销售一批名牌衬衫,已知所获利润y(元)与降价x(元)之间的关系是y=-2x2+60x+800,则利润获得最多为( )
A.15元 B.400元 C.800元 D.1250元
8.等腰三角形中,,,为边上一动点,,与的腰交于点,连结,设为,的面积为,则关于的函数关系的图象大致是( )
A. B. C. D.
二、填空题
9.如图,小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为(0,),则实心球飞行的水平距离OB的长度为 m.
10.如图,一个小球在并不光滑但均匀的水平地面上滚动,下表是小球s内滚动的路程(单位:m)的一些数据:
时间 0 1 2 3 5
路程 0 10
已知是关于的二次函数,则当时,的值为 .
11.如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度为 米.
12.月日晚时,南昌以天空为幕,以烟花为笔,举办了一场盛大的“风景这边独好”——南昌市国庆烟花晚会,热烈庆祝伟大祖国岁生日.其中,一种新型礼炮的升空高与飞行时间的关系式是,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要时间为 .
13.如图,P是抛物线y=x2﹣x﹣4在第四象限的一点,过点P分别向x轴和y轴作垂线,垂足分别为A、B,则四边形OAPB周长的最大值为 .
三、解答题
14.如图,要建一个圆形喷水池,在池中心竖直安置一根水管,在水管的顶端A安一个喷水头,使喷出的抛物线形水柱与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m.以水管与地面的交点为原点,原点与水柱落地处所在直线为x轴,水管所在直线为y轴,建立平面直角坐标系,每个单位长度表示1m.
(1)求水管的长度.
(2)如图2,是图中抛物线上一动点,点与点P关于y轴对称,画出点所在的抛物线的草图,并直接写出点所在抛物线的解析式及自变量的取值范围.
(3)将水管OA喷水头往上平移m,求水柱落地处离池中心的距离.
15.掷实心球是中考体育项目之一,为了在体育中考中取得更好的成绩,小鹏积极训练,如图所示,实心球经过的路线是一条抛物线,掷出时,实心球出手处距离地面的高度是2,实心球的落地点为处,以为原点,所在直线为轴,所在直线为轴建立平面直角坐标系,当实心球运行的水平距离为3时,达到最大高度3的处.
(1)求抛物线的解析式;
(2)若成绩想要达到80分,实心球出手处至球落地处的水平距离至少为8.4,小鹏此次投掷的成绩能上80分吗?
16.如图,已知抛物线y=x2-(k+1)x+1的顶点A在x轴的负半轴上,且与一次函数y=-x+1交于点B和点C
(1)求k的值;
(2)求ABC的面积.
17.如图,要建一个圆形喷水池,在池中心竖直放置一根水管,在水管的顶端A安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为,水柱落地处离池中心.
(1)求水管的长度;
(2)若在喷水池中竖直放置一盏高为的景观射灯,且景观射灯的顶端F恰好碰到水柱,求景观射灯与之间的水平距离;
(3)现计划扩建喷水池,升高水管,使落水点与水管之间的距离为,已知水管升高后,喷水头喷出的水柱形状和对称轴不变,则水管要升高多少?
18.小晨家在毛竹产量很高的山区,现打算建立一个以毛竹为原材料,生产工艺品和座椅的加工厂.第一批生产工艺品和座椅各50件,售后统计,工艺品平均每件利润是160元,座椅平均每件利润是19元,调研发现:
①工艺品每增加1件,工艺品的平均每件利润减少2元;每减少1件,工艺品的平均每件利润增加2元.
②座椅的平均每件利润始终不变.
小晨计划第二批生产工艺品和座椅共100件,设生产的工艺品比第一批增加x件,第二批生产的工艺品和座椅售完后的利润分别为,(单位:元)
(1)用含x的代数式分别表示,;
(2)当x取何值时,第二批生产的工艺品和座椅售完后获得的总利润W最大,最大总利润是多少?
19.一名身高为1.8m的篮球运动员甲在距篮筐(点B)水平距离4m处跳起投篮,篮球准确落入篮筐,已知篮球的运动路线是抛物线,篮球在运动员甲头顶上方0.25m处(点A)出手,篮球在距离篮筐水平距离为1.5m处达到最大高度3.5m,以水平地面为x轴,篮球达到最大高度时的铅直方向为y轴,建立如图所示的平面直角坐标系.
(1)求篮球运动路线(抛物线)的函数解析式;
(2)求篮球出手时,运动员甲跳离地面的高度是多少米?
(3)已知运动员乙跳离地面时,最高能摸到3.3运动员乙在运动员甲与篮筐之间的什么范围内能在空中截住球?
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】求出时的月份,以及时的月份,即可.
【详解】解:∵,
∴当时,,
解得:;
又当时,;
∴企业停产的月份为1月、2月和12月;
故选D.
【点睛】本题考查二次函数的实际应用.理解题意,正确的求出自变量的值,是解题的关键.
2.B
【分析】根据题意和二次函数的性质,可以确定出对称x的取值范围,从而可以解答本题.
【详解】解:由图象可得,
该函数的对称轴x>且x<50,
∴37.5<x<50,
∴此燃气灶烧开壶水最节省燃气的旋钮角度约为40°,
故选:B.
【点睛】本题考查二次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
3.C
【详解】试题解析:∵高度h和飞行时间t 满足函数关系式:h=-5(t-1)2+6,
∴当t=1时,小球距离地面高度最大,
∴h=-5×(1-1)2+6=6米,
故选C.
考点:二次函数的应用.
4.C
【分析】根据铅球落地时,高度y=0,把实际问题可理解为当y=0时,求x的值即可.
【详解】解:当y=0时,即yx2x0,
解得:x=﹣2(舍去),x=10.
∴该生此次实心球训练的成绩为10米.
故选:C.
【点睛】本题考查了二次函数的应用中函数式中变量与函数表达的实际意义,需要结合题意,取函数或自变量的特殊值列方程求解是解题关键.
5.A
【分析】先分别算出各种方案中图形的面积,再比较大小求解.
【详解】解:设围成的图形的面积为平方米,
方案一:设圆的半径为米,则:,
解得:,
(平方米);
方案二:设与墙相邻的边长为米,则另一边为米,
由题意得:,
,
当时,有最大值,最大值为32平方米;
方案三:围栏的长为16米,
等腰三角形的腰为8米,
当顶角为直角时,面积最大,此时(平方米);
,
∴最佳方案是方案一;
故选A
【点睛】本题考查了二次函数的应用,计算图形的面积是解题的关键.
6.B
【分析】本题主要考查了二次函数的应用,根据已知建立直角坐标系,进而求出二次函数解析式,再通过把代入抛物线解析式求出水面宽度即可,根据已知建立坐标系从而得出二次函数解析式是解决问题的关键.
【详解】解:建立平面直角坐标系,设横轴通过,纵轴轴通过中点且通过点,则通过画图可得为原点,抛物线以轴为对称轴,且经过、两点,和可求出为的一半为米,抛物线的顶点坐标为,
,
设顶点式为,代入点的坐标,
得出,
解得:,
抛物线的解析式为:,
当水面下降2.5米时,即当时,,
解得:,
水面的宽度为(米),
故选:B.
7.D
【分析】将函数关系式转化为顶点式,然后利用开口方向和顶点坐标即可求出最多的利润.
【详解】解:y=-2x2+60x+800=-2(x-15)2+1250
∵-2<0
故当x=15时,y有最大值,最大值为1250
即利润获得最多为1250元
故选:D.
【点睛】此题考查的是利用二次函数求最值,掌握将二次函数的一般式转化为顶点式求最值是解决此题的关键.
8.D
【分析】过B作BD⊥AC于D,则AD=CD=4,由勾股定理可得BD=3,再分两种情况进行讨论:当Q在AB上时,求得△CPQ面积y=PQ×CP=-x2+3x(0≤x<4);当Q在BC上时,求得△CPQ面积y=PQ×CP=x2-6x+24(4≤x≤8),据此判断函数图象即可.
【详解】解:过作于,则,
∴由勾股定理可得,,
如图所示,当在上时,
由,可得,
∴,
又∵,
∴面积;
如图所示,当在上时,,
由,可得,
∴面积,
∴当时,函数图象是开口向下的抛物线;当时,函数图象是开口向上的抛物线.
故选:D.
【点睛】本题主要考查了动点问题的函数图象,解题时注意:二次函数的图象为抛物线,开口方向由二次项的系数符号决定,用图象解决问题时,要理清图象的含义即会识图.
9.8
【分析】根据出手点A的坐标为(0,),求出函数关系式,再令y=0可解得答案.
【详解】解:把A(0,)代入得:
,
∴,
∴,
令y=0得,
解得x=2(舍去)或x=8,
∴实心球飞行的水平距离OB的长度为8m,
故答案为:8.
【点睛】本题考查二次函数的应用,解题的关键是理解题意,能用待定系数法求出函数关系式.
10.
【分析】本题考查了二次函数的应用.利用待定系数法得到函数解析式,再将代入计算即可得到答案.
【详解】解:设二次函数的解析式为,
将,代入得,
解得,
∴二次函数的解析式为,
当时,,
故答案为:
11.
【分析】根据已知得出直角坐标系,进而求出二次函数解析式,再通过把代入抛物线解析式得出水面宽度,即可得出答案.
【详解】解:建立平面直角坐标系,设横轴x通过,纵轴y通过中点O且通过C点,如图,
抛物线以y轴为对称轴,且经过A,B两点,和可求出为的一半,为2米,抛物线顶点C坐标为,点A坐标为,
通过以上条件可设顶点式,
代入A点坐标,可得,
解得:,所以抛物线解析式为,
当水面下降1米,通过抛物线在图上的观察可转化为:
当时,对应的抛物线上两点之间的距离,也就是直线与抛物线相交的两点之间的距离,
可以通过把代入抛物线解析式得出:
,解得:,
所以水面宽度为米,
故答案为:.
【点睛】此题主要考查了二次函数的应用,根据已知建立坐标系从而得出二次函数解析式是解决问题的关键.
12./4秒
【分析】把二次函数写成顶点式,顶点为礼炮点火升空到最高点处的位置,则顶点的横坐标即为所求.
【详解】∵,
∵ ,
∴当时,函数有最大值,为,
∴.这种礼炮点火升空到最高点处引爆,则从点火升空到引爆需要的时间为,
故答案为:.
【点睛】此题考查了二次函数在实际问题中的应用,熟练掌握二次函数的性质是解题的关键.
13.10
【分析】设P(x,x2﹣x﹣4)根据矩形的周长公式得到C=﹣2(x﹣1)2+10.根据二次函数的性质来求最值即可.
【详解】解:设P(x,x2﹣x﹣4),
四边形OAPB周长=2PA+2OA=﹣2(x2﹣x﹣4)+2x=﹣2x2+4x+8=﹣2(x﹣1)2+10,
当x=1时,四边形OAPB周长有最大值,最大值为10.
故答案为10.
【点睛】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的性质.
14.(1)
(2)图像如图所示,
(3)
【分析】对于(1),根据题意可知图象的顶点坐标为,经过点,再设顶点式并求出,令可得答案;
对于(2),先画出图象,再确定点的坐标,进而得出关系式,并求出自变量取值范围;
对于(3),先求出平移后的关系式,再令,可得答案.
【详解】(1)根据题意可知图象的顶点坐标为,经过点.
设二次函数的关系式为,根据题意,得
.
又∵图象经过点,
∴,
解得,
∴二次函数的关系式为.
当时,,
∴m.
(2)如图所示.
由(1),得二次函数的关系式为.
则点关于y轴对称的点的坐标为,
∴点所在抛物线的关系式为();
(3)将水管喷头往上平移,可得关系式为.
令,得,
解得或(舍).
所以水柱落地后离中心的距离是.
【点睛】本题主要考查了待定系数法求二次函数关系式,画二次函数图像,二次函数图像的平移,二次函数的对称性等,选择适当的关系式是解题的关键.
15.(1)
(2)不能
【分析】本题主要考查了二次函数的应用、解一元二次方程、实数比较大小等知识,正确解得该抛物线解析式是解题关键.
(1)根据题意,设该抛物线解析式为,然后将将点代入求解即可;
(2)对于抛物线,令,解得的值,进而确定点坐标,根据题意比较点横坐标与8.4的大小,即可获得答案.
【详解】(1)解:根据题意,可得,该抛物线顶点坐标为,
设该抛物线解析式为,
将点代入,可得,
解得,
∴该抛物线解析式为;
(2)对于抛物线,
令,可得,
整理可得,
解得,,
∵点在轴正半轴上,
∴,
又∵,
∴小鹏此次投掷的成绩不能上80分.
16.(1)k=-3;(2)3
【分析】(1)根据抛物线顶点A在x轴的负半轴上,得到△=0,故可求出m;
(2)求出A,B,C坐标,根据割补法即可求解.
【详解】(1)依题意可得[-(k+1)] 2-4=0
解得k=1或k=-3
∵顶点A在x轴的负半轴上,
∴-(k+1)>0
即k<-1
∴k=-3
∴y=x2+2x+1=(x+1)2,故A(-1,0)
(2)令一次函数x=0,代入y=-x+1=1
∴C(0,1)
联立
解得或
∴B(-3,4)
∴S△ABC=3×4-×3×3-×4×2-×1×1=3.
【点睛】此题主要考查二次函数的图象与几何综合,解题的关键是熟知二次函数的图象与性质.
17.(1)水管的长度为
(2)景观射灯与之间的水平距离为
(3)水管要升高
【分析】该题考查了二次函数的应用,此类问题一般涉及抛球、投篮、隧道、拱桥、喷泉水柱等.解决此类问题的关键是理解题目中的条件所表示的几何意义.
(1)用待定系数法求出抛物线的表达式,令,即可求解;
(2)把代入解析式,即可求解;
(3)设水管要升高,求出扩建后抛物线的表达式,即可求解;
【详解】(1)解:由题意可知,,
设抛物线的表达式为,
∵点在抛物线上,
∴,
解得,
∴抛物线的表达式为.
令,得,
∴水管的长度为.
(2)把代入得,
解得(舍去),
∴景观射灯与之间的水平距离为;
(3)设水管要升高,
则扩建后抛物线的表达式为,
把代入得,
解得,
∴水管要升高.
18.(1),;(2)当时,第二批生产的工艺品和座椅售完后获得的总利润W最大,最大总利润是9160元
【分析】(1)设第二批生产的工艺品比第一批增加x件,则工艺品有件,座椅有件,根据“利润=件数每件的利润”可得函数解析式;
(2)将工艺品的利润加上座椅的利润可得总利润关于x的函数解析式,配方成顶点式,利用二次函数的性质求解可得.
【详解】解:设第二批生产的工艺品比第一批增加x件,则工艺品有件,座椅有件,
由题意得:,
;
根据题意,得:
,
,
,
,
∵,且x为整数,
当时,W取得最大值,最大值为9160,
答:当时,第二批生产的工艺品和座椅售完后获得的总利润W最大,最大总利润是9160元.
【点睛】本题主要考查二次函数的应用,解题的关键是理解题意,找到题目蕴含的相等关系,据此列出函数解析式及二次函数的性质.
19.(1)
(2)0.2米
(3)乙在运动员距离甲1.5米之内以及篮板0.5米之内能在空中截住球.
【分析】(1)设抛物线的表达式为,依题意可知图象经过的坐标,由此可得a的值即可;
(2)当x=-2.5时,y=-0.2×(-2.5)2+3.5=2.25,即可得到结论.
(3)当y=3.3代入函数解析式,求出x的值,即可得出答案.
【详解】(1)∵抛物线的顶点坐标为(0,3.5),
∴设抛物线的解析式为.
由题意可知,抛物线上的点的坐标为(1.5,3.05).
∴,
解得,
∴抛物线的解析式为;
(2)设篮球出手时,运动员甲跳离地面的高度为.
4-1.5=2.5,0.25+1.8=2.05.
由题意可得点A的坐标为,
∴,
∴.
∴篮球出手时,运动员跳离地面的高度是0.2米;
(3)由题意可得出:y=3.3,
则3.3=-0.2x2+3.5
解得:x1=1,x2=-1,
∴1.5-1=0.5,-2.5-(-1)=1.5,
∴乙在运动员距离甲1.5米之内以及篮板0.5米之内能在空中截住球.
【点睛】此题主要考查了二次函数的应用;建立合适的平面直角坐标系是解决本题的突破点;求得球出手时距离地面的高度是解决本题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
