6.4.3 余弦定理、正弦定理 3.余弦定理、正弦定理应用举例 练习(含解析)-2024-2025学年高一下学期数学人教A版(2019)必修第二册
文档属性
| 名称 | 6.4.3 余弦定理、正弦定理 3.余弦定理、正弦定理应用举例 练习(含解析)-2024-2025学年高一下学期数学人教A版(2019)必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 163.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-10 14:39:17 | ||
图片预览



文档简介
3.余弦定理、正弦定理应用举例
一、选择题
1.已知两座灯塔A和B与海洋观察站C间的距离相等,灯塔A在观察站C的北偏东40°方向上,灯塔B在观察站C的南偏东60°方向上,则灯塔A在灯塔B的 ( )
A.北偏东10°方向上
B.北偏西10°方向上
C.南偏东10°方向上
D.南偏西10°方向上
2.某观察站C与两灯塔A,B间的距离分别为3 km和5 km,测得灯塔A在观察站C北偏西50°方向上,灯塔B在观察站C北偏东70°方向上,则两灯塔A,B间的距离为 ( )
A. km
B. km
C.7 km
D. km
3.某地为响应生态文明建设的号召,大力开展“青山绿水”工程,造福于民,拟对该地某湖泊进行治理,在治理前,需测量该湖泊的相关数据.如图所示,测得角A=23°,C=120°,AC=60米,则A,B间的距离约为(参考数据:sin 37°≈0.6) ( )
A.60米 B.120米
C.150米 D.300米
4.如图,为测量塔AB的高度,某人在与塔底A在同一水平线上的点C处测得∠ACB=45°,再沿AC向前行走20(-1)米到达点D,测得∠ADB=30°,则塔高为 ( )
A.40 米 B.20 米
C.40米 D.20米
5.已知某船正以30(-1)海里/时的速度向正北方向航行,该船在A点处发现北偏东30°方向的海面上有一个小岛,继续航行20分钟到达B点,发现该小岛在北偏东45°方向上,若该船向北继续航行,则船与小岛的最小距离为 ( )
A.6海里 B.8海里
C.10海里 D.12海里
6.如图,飞机的航线和山顶在同一个铅垂面内,若飞机的高度为海拔19 km,速度为300 km/h,飞行员先在A处看到山顶C的俯角为45°,经过2 min后,又在B处看到山顶C的俯角为75°,则山顶C的海拔约为(结果精确到0.1,参考数据:≈1.732) ( )
A.4.3 km B.5.3 km
C.6.3 km D.13.7 km
7.如图所示,为了测量A,B处岛屿间的距离,小张在D处观测,测得A,B分别在D处的北偏西30°,北偏东30°方向,再往正东方向行驶10海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为 ( )
A.5 海里 B.5(1+) 海里
C.10 海里 D.10海里
8.(多选题)如图,有A,B,C三艘渔船在海岛D附近作业,D在A的东北方向,D在B的北偏东30°方向,C在B的北偏东60°方向,B在A的正东方向,已知A,B相距(-1)a km,B,C相距a km,则 ( )
A.D在C的北偏西60°方向
B.D在C的北偏西30°方向
C.D,C相距a km
D.D,C相距a km
9.(多选题)如图所示,在山脚A处测得山顶上一建筑物CD的顶端C对于山坡AD的斜度为15°,向山顶前进100 m到达B处,又测得C对于山坡AD的斜度为45°,若CD=50 m,山坡的坡角为θ,则下列说法正确的是 ( )
A.cos θ=-1
B.cos θ=-1
C.山脚A处与建筑物CD的顶端C的距离为100m
D.山脚A处与建筑物CD的顶端C的距离为100 m
二、填空题
10.一艘船以15 km/h的速度向正东方向航行,在A处看到一个灯塔M在北偏东60°的方向上,行驶4 h后到达B处,看到灯塔M在北偏东15°的方向上,这时船与灯塔M的距离为 km.
11.海上有三个小岛A,B,C,测得∠BAC=135°,AB=6,AC=3,若在B,C两岛的连线上建一座灯塔D,使得灯塔D到A,B两岛之间的距离相等,则B,D之间的距离为 .
12.[2024·华师大一附中高一期中] 如图,为测量雕像AB的高度及观景点C与F之间的距离(B,C,D,F在同一水平面上,雕像垂直该水平面于点B,且B,C,D三点共线),某校研究性学习小组同学在C,D,F三点处测得顶点A的仰角分别为60°,30°,45°,若∠FCB=45°,CD=50米,则该雕像的高度为 米,观景点C与F之间的距离为 米.
三、解答题
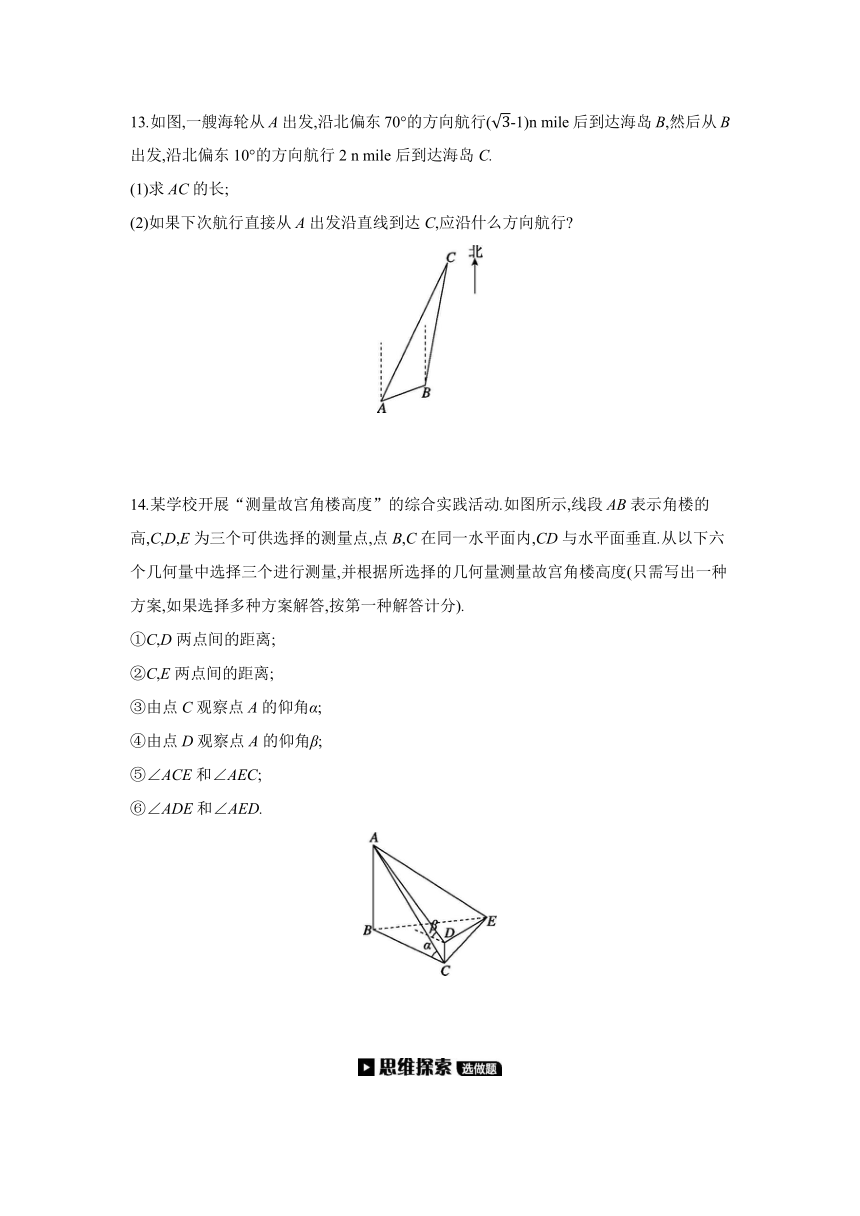
13.如图,一艘海轮从A出发,沿北偏东70°的方向航行(-1)n mile后到达海岛B,然后从B出发,沿北偏东10°的方向航行2 n mile后到达海岛C.
(1)求AC的长;
(2)如果下次航行直接从A出发沿直线到达C,应沿什么方向航行
14.某学校开展“测量故宫角楼高度”的综合实践活动.如图所示,线段AB表示角楼的高,C,D,E为三个可供选择的测量点,点B,C在同一水平面内,CD与水平面垂直.从以下六个几何量中选择三个进行测量,并根据所选择的几何量测量故宫角楼高度(只需写出一种方案,如果选择多种方案解答,按第一种解答计分).
①C,D两点间的距离;
②C,E两点间的距离;
③由点C观察点A的仰角α;
④由点D观察点A的仰角β;
⑤∠ACE和∠AEC;
⑥∠ADE和∠AED.
15.海洋蓝洞是地球罕见的自然地理现象,被誉为“地球给人类保留宇宙秘密的最后遗产”.若要测量如图所示的蓝洞的口径A,B两点间的距离,现在群岛上取两点C,D,测得CD=80米,∠ADB=135°,∠BDC=∠DCA=15°,∠ACB=120°,则A,B两点间的距离为 米.
16.如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道(索道为直线)乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min.在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车做匀速直线运动的速度为130 m/min,山路AC的长为1260 m,经测量,cos A=,cos C=.
(1)求索道AB的长.
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短
(3)为使两位游客在C处互相等待的时间不超过3 min,乙步行的速度应控制在什么范围内
3.余弦定理、正弦定理应用举例
1.B [解析] 如图,由题意知AC=BC,∠ACB=80°,所以∠CBA=50°,又α+∠CBA=60°,所以α=10°,即A在B的北偏西10°方向上.故选B.
2.C [解析] 由题意,在△ABC中,AC=3 km,BC=5 km,∠ACB=120°,由余弦定理可得,AB2=32+52-2×3×5×cos 120°=49,∴AB=7 km.故选C.
3.C [解析] 由题意知B=180°-A-C=37°.在△ABC中,由正弦定理得=,即=,所以AB=≈150(米).故选C.
4.D [解析] 在Rt△ABC中,设AB=x米,则由∠ACB=45°,可知AC=x米.在Rt△ABD中,因为AD=[x+20(-1)]米,∠ADB=30°,所以=tan 30°,即=,解得x=20,即塔高为20米.故选D.
5.C [解析] 如图所示,设小岛在C处,过C作CD⊥AD,垂足为D,由题意知A=30°,∠DBC=45°,AB=×30(-1)=10(-1)(海里).在△ABC中,∠ABC=135°,则∠ACB=15°,由正弦定理得=,所以BC==
==10(海里),所以CD=BCsin 45°=10×=10(海里),故选C.
6.B [解析] 过点C作直线AB的垂线,垂足为D.由题意得AB=300×=10(km),∠ACB=30°.因为=,所以BC=AB·=10(km),又sin 75°=sin(45°+30°)=,所以CD=BC·sin∠CBD=10×=5(+1)≈13.66(km),故山顶C的海拔约为19-13.66≈5.3(km).故选B.
7.C [解析] 由题可得CD=10海里,∠ADC=120°,∠BDC=60°,∠BCD=90°,∠ACD=30°,所以∠CAD=30°,∠ADB=60°.在△ACD中,可得AD=CD=10海里.在Rt△BCD中,因为∠BDC=60°,∠BCD=90°,所以BD=2CD=20海里.在△ABD中,由余弦定理可得AB2=AD2+BD2-2AD·BDcos 60° =100+400-2×10×20×=300,所以AB=10 海里,即A,B两处岛屿间的距离为10 海里.故选C.
8.BC [解析] 如图所示,∠DAB=45°,∠DBE=60°,∠DBC=∠CBE=30°,∠ADB=15°,sin 15°=sin(45°-30°)=.在△ABD中,由正弦定理得=,解得BD=2a.在△BDC中,由余弦定理得DC2=BD2+BC2-2BD·BCcos∠DBC=a2,所以DC2+BC2=BD2,则∠BCD=90°,所以D在C的北偏西30°方向,且D,C相距a km.故选BC.
9.AC [解析] ∵∠CBD=45°,∠BAC=15°,∴∠ACB=30°.在△ABC中,由正弦定理得BC===50(-)(m).在△BCD中,由正弦定理得=,即=,∴sin∠BDC=-1,即sin(θ+90°)=-1,∴cos θ=-1,故A正确,B错误.在△ABC中,∠ABC=135°,由正弦定理得,=,故AC===100(m),故C正确,D错误.故选AC.
10.30 [解析] 如图,依题意有AB=15×4=60(km),∠MAB=30°,∠AMB=45°.在△AMB中,由正弦定理得=,所以BM=30 km.
11. [解析] 设BD=t,由余弦定理可得BC2=62+(3)2-2×6×3cos 135°=90,所以BC=3,则cos∠ABC==,解得t=.
12.25 [解析] 由题可知△ADC是等腰三角形,且AC=CD,得AC=50.在Rt△ABC中,AB=AC·sin∠ACB=50sin 60°=25,故雕像的高度为25米.在Rt△ABC中,AC=50,∠ACB=60°,所以CB=25.在Rt△ABF中,∠AFB=45°,AB=25,所以FB=25,又在△BCF中,∠BCF=45°,所以由余弦定理可得BF2=CF2+CB2-2CF·CB·cos 45°,可得CF=,故观景点C与F之间的距离为米.
13.解:(1)由题意知,在△ABC中,∠ABC=180°-70°+10°=120°,AB=(-1)n mile,BC=2 n mile.由余弦定理,得AC2=AB2+BC2-2AB×BC×cos∠ABC=(-1)2+4+2(-1)=6,所以AC= n mile.
(2)根据正弦定理可得=,
故sin∠CAB=sin∠ABC===,
又∠CAB∈(0°,60°),所以∠CAB=45°,
又70°-45°=25°,所以从A出发沿北偏东25°的方向航行 n mile即可到达C处.
14.解:若要求角楼的高,即AB的长,则必须知道一边的长,若知道C,D两点间的距离,即CD的长,则解△ACD和△ABC即可,此时可选①③④;若知道C,E两点间的距离,即CE的长,则解△ACE和△ABC即可,此时可选②③⑤.其他选择方案均不可求得AB的长.
若选①③④,由已知可得,∠ABC=∠BCD=,
在△ACD中,∠ACD=-α,∠ADC=+β,∠CAD=α-β,所以=,
所以AC=·CD,所以AB=AC·sin α=·CD,其中各个量均已知.
若选②③⑤,已知∠ACE和∠AEC,则∠CAE=π-∠ACE-∠AEC.在△ACE中,由正弦定理得==,
所以AC=·CE,
所以AB=ACsin α=·CE ,其中各个量均已知.
15.80 [解析] 在△ACD中,∵∠ACD=15°,∠ADC=150°,∴∠DAC=15°,由正弦定理得AC===40(+)(米).在△BCD中,∵∠BDC=15°,∠BCD=135°,∴∠DBC=30°,由正弦定理得BC==40(-)(米).在△ABC中,由余弦定理得AB2=AC2+BC2-2AC·BC·cos∠ACB=1600×(8+4)+1600×(8-4)+1600×(+)×(-)=1600×16+1600×4=32 000,∴AB=80米,故A,B两点间的距离为80 米.
16.解:(1)由题意得sin A=,sin C=.在△ABC中,sin B=sin(A+C)=sin Acos C+cos Asin C=.
由=,得AB==1040(m),所以索道AB的长为1040 m.
(2)假设乙出发t min后,甲、乙(乙在缆车上)两游客之间的距离为d m,此时甲行走了(100+50t)m,乙距离A处130t m,由余弦定理得d2=(100+50t)2+(130t)2-2×130t×(100+50t)×=200(37t2-70t+50).因为0≤t≤,即0≤t≤8,所以当t=时,甲、乙(乙在缆车上)两游客之间的距离最短.
(3)由=,得BC=sin A·=500(m).
=8,乙从B出发时,甲已经走了50×(2+8+1)=550(m),还需要走1260-550=710(m)才能到达C.设乙步行的速度为v m/min,由题意得-3≤-≤3,解得≤v≤,所以为了使两位游客在C处互相等待的时间不超过3 min,乙步行的速度(单位:m/min)应控制在内.
一、选择题
1.已知两座灯塔A和B与海洋观察站C间的距离相等,灯塔A在观察站C的北偏东40°方向上,灯塔B在观察站C的南偏东60°方向上,则灯塔A在灯塔B的 ( )
A.北偏东10°方向上
B.北偏西10°方向上
C.南偏东10°方向上
D.南偏西10°方向上
2.某观察站C与两灯塔A,B间的距离分别为3 km和5 km,测得灯塔A在观察站C北偏西50°方向上,灯塔B在观察站C北偏东70°方向上,则两灯塔A,B间的距离为 ( )
A. km
B. km
C.7 km
D. km
3.某地为响应生态文明建设的号召,大力开展“青山绿水”工程,造福于民,拟对该地某湖泊进行治理,在治理前,需测量该湖泊的相关数据.如图所示,测得角A=23°,C=120°,AC=60米,则A,B间的距离约为(参考数据:sin 37°≈0.6) ( )
A.60米 B.120米
C.150米 D.300米
4.如图,为测量塔AB的高度,某人在与塔底A在同一水平线上的点C处测得∠ACB=45°,再沿AC向前行走20(-1)米到达点D,测得∠ADB=30°,则塔高为 ( )
A.40 米 B.20 米
C.40米 D.20米
5.已知某船正以30(-1)海里/时的速度向正北方向航行,该船在A点处发现北偏东30°方向的海面上有一个小岛,继续航行20分钟到达B点,发现该小岛在北偏东45°方向上,若该船向北继续航行,则船与小岛的最小距离为 ( )
A.6海里 B.8海里
C.10海里 D.12海里
6.如图,飞机的航线和山顶在同一个铅垂面内,若飞机的高度为海拔19 km,速度为300 km/h,飞行员先在A处看到山顶C的俯角为45°,经过2 min后,又在B处看到山顶C的俯角为75°,则山顶C的海拔约为(结果精确到0.1,参考数据:≈1.732) ( )
A.4.3 km B.5.3 km
C.6.3 km D.13.7 km
7.如图所示,为了测量A,B处岛屿间的距离,小张在D处观测,测得A,B分别在D处的北偏西30°,北偏东30°方向,再往正东方向行驶10海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为 ( )
A.5 海里 B.5(1+) 海里
C.10 海里 D.10海里
8.(多选题)如图,有A,B,C三艘渔船在海岛D附近作业,D在A的东北方向,D在B的北偏东30°方向,C在B的北偏东60°方向,B在A的正东方向,已知A,B相距(-1)a km,B,C相距a km,则 ( )
A.D在C的北偏西60°方向
B.D在C的北偏西30°方向
C.D,C相距a km
D.D,C相距a km
9.(多选题)如图所示,在山脚A处测得山顶上一建筑物CD的顶端C对于山坡AD的斜度为15°,向山顶前进100 m到达B处,又测得C对于山坡AD的斜度为45°,若CD=50 m,山坡的坡角为θ,则下列说法正确的是 ( )
A.cos θ=-1
B.cos θ=-1
C.山脚A处与建筑物CD的顶端C的距离为100m
D.山脚A处与建筑物CD的顶端C的距离为100 m
二、填空题
10.一艘船以15 km/h的速度向正东方向航行,在A处看到一个灯塔M在北偏东60°的方向上,行驶4 h后到达B处,看到灯塔M在北偏东15°的方向上,这时船与灯塔M的距离为 km.
11.海上有三个小岛A,B,C,测得∠BAC=135°,AB=6,AC=3,若在B,C两岛的连线上建一座灯塔D,使得灯塔D到A,B两岛之间的距离相等,则B,D之间的距离为 .
12.[2024·华师大一附中高一期中] 如图,为测量雕像AB的高度及观景点C与F之间的距离(B,C,D,F在同一水平面上,雕像垂直该水平面于点B,且B,C,D三点共线),某校研究性学习小组同学在C,D,F三点处测得顶点A的仰角分别为60°,30°,45°,若∠FCB=45°,CD=50米,则该雕像的高度为 米,观景点C与F之间的距离为 米.
三、解答题
13.如图,一艘海轮从A出发,沿北偏东70°的方向航行(-1)n mile后到达海岛B,然后从B出发,沿北偏东10°的方向航行2 n mile后到达海岛C.
(1)求AC的长;
(2)如果下次航行直接从A出发沿直线到达C,应沿什么方向航行
14.某学校开展“测量故宫角楼高度”的综合实践活动.如图所示,线段AB表示角楼的高,C,D,E为三个可供选择的测量点,点B,C在同一水平面内,CD与水平面垂直.从以下六个几何量中选择三个进行测量,并根据所选择的几何量测量故宫角楼高度(只需写出一种方案,如果选择多种方案解答,按第一种解答计分).
①C,D两点间的距离;
②C,E两点间的距离;
③由点C观察点A的仰角α;
④由点D观察点A的仰角β;
⑤∠ACE和∠AEC;
⑥∠ADE和∠AED.
15.海洋蓝洞是地球罕见的自然地理现象,被誉为“地球给人类保留宇宙秘密的最后遗产”.若要测量如图所示的蓝洞的口径A,B两点间的距离,现在群岛上取两点C,D,测得CD=80米,∠ADB=135°,∠BDC=∠DCA=15°,∠ACB=120°,则A,B两点间的距离为 米.
16.如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道(索道为直线)乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min.在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车做匀速直线运动的速度为130 m/min,山路AC的长为1260 m,经测量,cos A=,cos C=.
(1)求索道AB的长.
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短
(3)为使两位游客在C处互相等待的时间不超过3 min,乙步行的速度应控制在什么范围内
3.余弦定理、正弦定理应用举例
1.B [解析] 如图,由题意知AC=BC,∠ACB=80°,所以∠CBA=50°,又α+∠CBA=60°,所以α=10°,即A在B的北偏西10°方向上.故选B.
2.C [解析] 由题意,在△ABC中,AC=3 km,BC=5 km,∠ACB=120°,由余弦定理可得,AB2=32+52-2×3×5×cos 120°=49,∴AB=7 km.故选C.
3.C [解析] 由题意知B=180°-A-C=37°.在△ABC中,由正弦定理得=,即=,所以AB=≈150(米).故选C.
4.D [解析] 在Rt△ABC中,设AB=x米,则由∠ACB=45°,可知AC=x米.在Rt△ABD中,因为AD=[x+20(-1)]米,∠ADB=30°,所以=tan 30°,即=,解得x=20,即塔高为20米.故选D.
5.C [解析] 如图所示,设小岛在C处,过C作CD⊥AD,垂足为D,由题意知A=30°,∠DBC=45°,AB=×30(-1)=10(-1)(海里).在△ABC中,∠ABC=135°,则∠ACB=15°,由正弦定理得=,所以BC==
==10(海里),所以CD=BCsin 45°=10×=10(海里),故选C.
6.B [解析] 过点C作直线AB的垂线,垂足为D.由题意得AB=300×=10(km),∠ACB=30°.因为=,所以BC=AB·=10(km),又sin 75°=sin(45°+30°)=,所以CD=BC·sin∠CBD=10×=5(+1)≈13.66(km),故山顶C的海拔约为19-13.66≈5.3(km).故选B.
7.C [解析] 由题可得CD=10海里,∠ADC=120°,∠BDC=60°,∠BCD=90°,∠ACD=30°,所以∠CAD=30°,∠ADB=60°.在△ACD中,可得AD=CD=10海里.在Rt△BCD中,因为∠BDC=60°,∠BCD=90°,所以BD=2CD=20海里.在△ABD中,由余弦定理可得AB2=AD2+BD2-2AD·BDcos 60° =100+400-2×10×20×=300,所以AB=10 海里,即A,B两处岛屿间的距离为10 海里.故选C.
8.BC [解析] 如图所示,∠DAB=45°,∠DBE=60°,∠DBC=∠CBE=30°,∠ADB=15°,sin 15°=sin(45°-30°)=.在△ABD中,由正弦定理得=,解得BD=2a.在△BDC中,由余弦定理得DC2=BD2+BC2-2BD·BCcos∠DBC=a2,所以DC2+BC2=BD2,则∠BCD=90°,所以D在C的北偏西30°方向,且D,C相距a km.故选BC.
9.AC [解析] ∵∠CBD=45°,∠BAC=15°,∴∠ACB=30°.在△ABC中,由正弦定理得BC===50(-)(m).在△BCD中,由正弦定理得=,即=,∴sin∠BDC=-1,即sin(θ+90°)=-1,∴cos θ=-1,故A正确,B错误.在△ABC中,∠ABC=135°,由正弦定理得,=,故AC===100(m),故C正确,D错误.故选AC.
10.30 [解析] 如图,依题意有AB=15×4=60(km),∠MAB=30°,∠AMB=45°.在△AMB中,由正弦定理得=,所以BM=30 km.
11. [解析] 设BD=t,由余弦定理可得BC2=62+(3)2-2×6×3cos 135°=90,所以BC=3,则cos∠ABC==,解得t=.
12.25 [解析] 由题可知△ADC是等腰三角形,且AC=CD,得AC=50.在Rt△ABC中,AB=AC·sin∠ACB=50sin 60°=25,故雕像的高度为25米.在Rt△ABC中,AC=50,∠ACB=60°,所以CB=25.在Rt△ABF中,∠AFB=45°,AB=25,所以FB=25,又在△BCF中,∠BCF=45°,所以由余弦定理可得BF2=CF2+CB2-2CF·CB·cos 45°,可得CF=,故观景点C与F之间的距离为米.
13.解:(1)由题意知,在△ABC中,∠ABC=180°-70°+10°=120°,AB=(-1)n mile,BC=2 n mile.由余弦定理,得AC2=AB2+BC2-2AB×BC×cos∠ABC=(-1)2+4+2(-1)=6,所以AC= n mile.
(2)根据正弦定理可得=,
故sin∠CAB=sin∠ABC===,
又∠CAB∈(0°,60°),所以∠CAB=45°,
又70°-45°=25°,所以从A出发沿北偏东25°的方向航行 n mile即可到达C处.
14.解:若要求角楼的高,即AB的长,则必须知道一边的长,若知道C,D两点间的距离,即CD的长,则解△ACD和△ABC即可,此时可选①③④;若知道C,E两点间的距离,即CE的长,则解△ACE和△ABC即可,此时可选②③⑤.其他选择方案均不可求得AB的长.
若选①③④,由已知可得,∠ABC=∠BCD=,
在△ACD中,∠ACD=-α,∠ADC=+β,∠CAD=α-β,所以=,
所以AC=·CD,所以AB=AC·sin α=·CD,其中各个量均已知.
若选②③⑤,已知∠ACE和∠AEC,则∠CAE=π-∠ACE-∠AEC.在△ACE中,由正弦定理得==,
所以AC=·CE,
所以AB=ACsin α=·CE ,其中各个量均已知.
15.80 [解析] 在△ACD中,∵∠ACD=15°,∠ADC=150°,∴∠DAC=15°,由正弦定理得AC===40(+)(米).在△BCD中,∵∠BDC=15°,∠BCD=135°,∴∠DBC=30°,由正弦定理得BC==40(-)(米).在△ABC中,由余弦定理得AB2=AC2+BC2-2AC·BC·cos∠ACB=1600×(8+4)+1600×(8-4)+1600×(+)×(-)=1600×16+1600×4=32 000,∴AB=80米,故A,B两点间的距离为80 米.
16.解:(1)由题意得sin A=,sin C=.在△ABC中,sin B=sin(A+C)=sin Acos C+cos Asin C=.
由=,得AB==1040(m),所以索道AB的长为1040 m.
(2)假设乙出发t min后,甲、乙(乙在缆车上)两游客之间的距离为d m,此时甲行走了(100+50t)m,乙距离A处130t m,由余弦定理得d2=(100+50t)2+(130t)2-2×130t×(100+50t)×=200(37t2-70t+50).因为0≤t≤,即0≤t≤8,所以当t=时,甲、乙(乙在缆车上)两游客之间的距离最短.
(3)由=,得BC=sin A·=500(m).
=8,乙从B出发时,甲已经走了50×(2+8+1)=550(m),还需要走1260-550=710(m)才能到达C.设乙步行的速度为v m/min,由题意得-3≤-≤3,解得≤v≤,所以为了使两位游客在C处互相等待的时间不超过3 min,乙步行的速度(单位:m/min)应控制在内.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
