[学案+答案]人教版 必修二第五章“曲线运动”章末复习
文档属性
| 名称 | [学案+答案]人教版 必修二第五章“曲线运动”章末复习 | 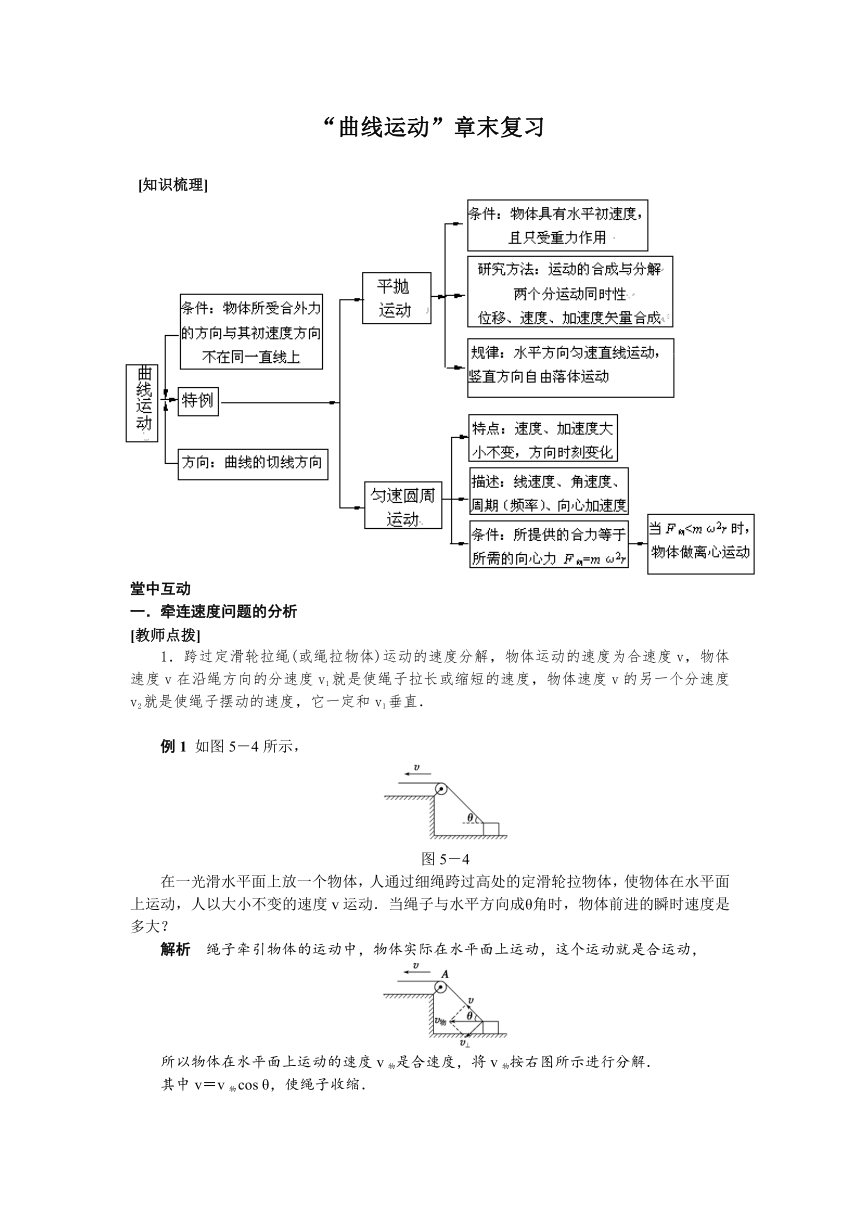 | |
| 格式 | zip | ||
| 文件大小 | 134.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-02-19 22:00:22 | ||
图片预览


文档简介
“曲线运动”章末复习
[知识梳理]
堂中互动
一.牵连速度问题的分析
[教师点拨]
1.跨过定滑轮拉绳(或绳拉物体)运动的速 ( http: / / www.21cnjy.com )度分解,物体运动的速度为合速度v,物体速度v在沿绳方向的分速度v1就是使绳子拉长或缩短的速度,物体速度v的另一个分速度v2就是使绳子摆动的速度,它一定和v1垂直.
例1 如图5-4所示,
图5-4
在一光滑水平面上放一个物体,人通过细绳跨过 ( http: / / www.21cnjy.com )高处的定滑轮拉物体,使物体在水平面上运动,人以大小不变的速度v运动.当绳子与水平方向成θ角时,物体前进的瞬时速度是多大?
解析 绳子牵引物体的运动中,物体实际在水平面上运动,这个运动就是合运动,
所以物体在水平面上运动的速度v物是合速度,将v物按右图所示进行分解.
其中v=v物cos θ,使绳子收缩.
v⊥=v物sin θ,使绳子绕定滑轮上的A点转动.
所以v物=.
答案
二、匀速圆周运动的问题
[教师点拨] .1.圆周运动的运动学分析
(1)正确理解描述圆周运动的快慢的物理量及其相互关系
线速度、角速度、周期和转速都可描述圆周运动 ( http: / / www.21cnjy.com )的快慢,但意义不同.线速度描述做圆周运动的物体沿圆周运动的快慢.若比较两物体沿圆周运动的快慢,则只看线速度大小即可;而角速度、周期和转速描述做圆周运动的物体绕圆心转动的快慢,由ω==2πn可知,ω越大,T越小,n越大,则物体转动得越快,反之则越慢.三个物理量知其中一个,另两个也就成为已知量.
(2)对公式v=rω及a==rω2的理解
①由v=rω知,r一定时,v与ω成正比;ω一定时,v与r成正比;v一定时,ω与r成反比.
②由a==rω2知,在v一定时,a与r成反比;在ω一定时,an与r成正比.
2.正交分解法处理圆周运动的受力
解决圆周运动问题的关键是正确地对物体进行受力分析,搞清向心力来源.
由于做圆周运动的物体,其受 ( http: / / www.21cnjy.com )力并不一定在它的运动平面上,所以在对物体进行受力分析时往往要进行正交分解.对圆周运动进行分析时,建立的坐标系不是恒定不变的,而是在每一个瞬间建立坐标系.
(1)匀速圆周运动:采用正交分解法,其 ( http: / / www.21cnjy.com )坐标原点是做圆周运动的物体(视为质点),相互垂直的两个坐标轴中,一定有一个坐标轴的正方向沿着半径指向圆心.
说明 若做匀速圆周运动的物体仅受两个力的作用,也可用直接合成法确定向心力,合力一定指向圆心.
(2)变速圆周运动:采用正交分解法 ( http: / / www.21cnjy.com ),有一个坐标轴的正方向沿着半径指向圆心.加速度沿半径方向的分量an(指向圆心)即为向心加速度,其大小为an==rω2;加速度沿轨迹切线方向的分量at即为切向加速度.
合力沿半径方向的分量Fn(或所有外 ( http: / / www.21cnjy.com )力沿半径方向分力的矢量和)提供向心力,其作用是改变速度的方向;其大小为:Fn=m=mω2r.合力沿切线方向的分力Ft(或所有外力沿切线方向的分力的矢量和)使物体产生切向加速度,其作用是改变速度的大小,其大小为Ft=mat.
3.处理匀速圆周运动问题的基本步骤
(1)确定做匀速圆周运动的物体作为研究对象.
(2)确定圆周运动的轨道平面、圆心位置和半径.
(3)对研究对象进行受力分析,作出受力示意图.
(4)运用平行四边形定则或正交分解法求出向心力Fn.
(5)根据向心力Fn=m=mω2r=mr,选择其中一种公式列方程求解.
1.传动运动
例2图中所示为一皮带传www.动装置,右轮的半径为r,a是它边缘上的一点,左侧是一轮轴,大轮的半径为4r,小轮的半径为2r,b点在小轮上,到小轮中心的距离为r,c点和d点分别位于小轮和大轮的边缘上,若在传动过程中,皮带不打滑,则( )
A.ab两点的线速度大小相www.等 B.ab两点的角速度大小相等
C.ac两点的线速度大小相等 D.ad两点的向心加速度大小相等
【解析】C选项皮带传动的两轮皮带www.接触处的线速度大小相等,C选项正确。
A选项bc角速度相等,线速度之比为1:2,所以ab线速度之比为2:1,A选项错误。
B选项ac两点的线速度大www.小相等,角速度之比为2:1,bc角速度相等,所以ab角速度之比为2:1,B选项错误。D选项,,所以D选项正确。
【答案】CD
2. 圆锥摆问题
例3有一种叫“飞椅”的游乐项目,示意图如图所示,长为L的钢绳一端系着座椅,另一端固定在半径为r的水平转盘边缘,转盘可绕穿过其中心的竖直轴转动.当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ,不计钢绳的重力,求转盘转动的角速度ω与夹角θ的关系.
( http: / / www.21cnjy.com )
【解析】设转盘转动角速度ω时,夹角为θ,座椅到中心轴的距离为
R=r+Lsinθ①
对座椅受力分析,由牛顿第二定律有
F合=mgtanθ=mRω2②
由①②两式联立得
【答案】
点评:圆锥摆是运动轨迹在水平面内的一种典型的 ( http: / / www.21cnjy.com )匀速圆周运动.其特点是由物体所受的重力与弹力的合力充当向心力,向心力的方向水平,也可以说是其中弹力的水平分力提供向心力(弹力的竖直分力和重力平衡),“飞机在水平面内做匀速圆周飞行”等在水平面内的匀速圆周运动的问题都属于此类问题.
3. 汽车过拱桥问题
例4有一辆质量为1.2t的小汽车驶上半径为50m的圆弧形拱桥。问:
①汽车到达桥顶的速度为10m/s时对桥的压力是多大?
②汽车以多大的速度经过桥顶时恰好对桥没有压力作用而腾空?
③设想拱桥的半径增www.大到与地 ( http: / / www.21cnjy.com )球半径一样,那么汽车要在这样的桥面上腾空,速度要多大?(重力加速度取10 m/s2,地球半径R取6.4×103 km)
【解析】①根据牛顿第www.二定律:
解得:,根据牛顿第三定律:
②根据牛顿第二定律:
解得:
③ 根据牛顿第二定www.律:
解得:
三、圆周运动的临界问题
[教师点拨] 4.临界问题的分析
(1)当物体从某种特性变 ( http: / / www.21cnjy.com )化为另一种特性时,发生质的飞跃的转折状态,通常叫做临界状态,出现临界状态时,既可理解为“恰好出现”,也可理解为“恰好不出现”.
(2)解决临界问题的常用方法
①极限法:把物理问题(或过程)推向极端,从而使临界现
象显露,达到尽快求解的目的.
②假设法:有些物理过程中没有明显出现临界问题的线索,但在变化过程中可能出现临界问题.
(3)关于临界问题总是出现在变速圆周运动中,而竖直平面内的圆周运动是最典型的变速圆周运动.
在竖直平面内的圆周运动一般不是匀速圆周运动,但物体经最高点或最低点时,所受的重力与其他力的合力指向圆心,提供向心力.
①
图5-3
用绳子系物体或物体沿轨道内侧运动(如图5-3所示)
此种情况下,如果物体恰能通过最高点,即 ( http: / / www.21cnjy.com )绳子的拉力或轨道对物体的支持力等于零,只有重力提供向心力,即mg=,得临界速度v0=.当物体的速度大于v0时,才能经过最高点.
②用杆固定物体在竖直平面内做圆周运动
此种情况下,由于物体所受的重力可以由杆 ( http: / / www.21cnjy.com )给它的向上的支持力来平衡,所以在最高点时的速度可以为零.当物体在最高点的速度v≥0时,物体就可以完成一个完整的圆周运
例5 在光滑平面中,有一转动轴垂直于此平面,交点O的上方h处固定一细绳的一端,绳的另一端固定一质量为m的小球B,绳长AB=l>h,小球可随转动轴转动并在光滑水平面上做匀速圆周运动,如图5-5所示,要使球不离开水平面,转动轴的转速的最大值是( )
A. B.π C. D.2π
解析 如右图所示,
以小球为研究对象,小球受三个力的作 ( http: / / www.21cnjy.com )用,重力mg、水平面支持力FN、绳子拉力F.在竖直方向合力为零,在水平方向所需向心力为,而R=htan θ,得
Fcos θ+FN=mg
Fsin θ==mω2R=m4π2n2R=m4π2n2htan θ
当球即将离开水平面时,FN=0,转速n有最大值.
FN=mg-m4π2n2h=0
n= ,故选A.
答案 A
[知识梳理]
堂中互动
一.牵连速度问题的分析
[教师点拨]
1.跨过定滑轮拉绳(或绳拉物体)运动的速 ( http: / / www.21cnjy.com )度分解,物体运动的速度为合速度v,物体速度v在沿绳方向的分速度v1就是使绳子拉长或缩短的速度,物体速度v的另一个分速度v2就是使绳子摆动的速度,它一定和v1垂直.
例1 如图5-4所示,
图5-4
在一光滑水平面上放一个物体,人通过细绳跨过 ( http: / / www.21cnjy.com )高处的定滑轮拉物体,使物体在水平面上运动,人以大小不变的速度v运动.当绳子与水平方向成θ角时,物体前进的瞬时速度是多大?
解析 绳子牵引物体的运动中,物体实际在水平面上运动,这个运动就是合运动,
所以物体在水平面上运动的速度v物是合速度,将v物按右图所示进行分解.
其中v=v物cos θ,使绳子收缩.
v⊥=v物sin θ,使绳子绕定滑轮上的A点转动.
所以v物=.
答案
二、匀速圆周运动的问题
[教师点拨] .1.圆周运动的运动学分析
(1)正确理解描述圆周运动的快慢的物理量及其相互关系
线速度、角速度、周期和转速都可描述圆周运动 ( http: / / www.21cnjy.com )的快慢,但意义不同.线速度描述做圆周运动的物体沿圆周运动的快慢.若比较两物体沿圆周运动的快慢,则只看线速度大小即可;而角速度、周期和转速描述做圆周运动的物体绕圆心转动的快慢,由ω==2πn可知,ω越大,T越小,n越大,则物体转动得越快,反之则越慢.三个物理量知其中一个,另两个也就成为已知量.
(2)对公式v=rω及a==rω2的理解
①由v=rω知,r一定时,v与ω成正比;ω一定时,v与r成正比;v一定时,ω与r成反比.
②由a==rω2知,在v一定时,a与r成反比;在ω一定时,an与r成正比.
2.正交分解法处理圆周运动的受力
解决圆周运动问题的关键是正确地对物体进行受力分析,搞清向心力来源.
由于做圆周运动的物体,其受 ( http: / / www.21cnjy.com )力并不一定在它的运动平面上,所以在对物体进行受力分析时往往要进行正交分解.对圆周运动进行分析时,建立的坐标系不是恒定不变的,而是在每一个瞬间建立坐标系.
(1)匀速圆周运动:采用正交分解法,其 ( http: / / www.21cnjy.com )坐标原点是做圆周运动的物体(视为质点),相互垂直的两个坐标轴中,一定有一个坐标轴的正方向沿着半径指向圆心.
说明 若做匀速圆周运动的物体仅受两个力的作用,也可用直接合成法确定向心力,合力一定指向圆心.
(2)变速圆周运动:采用正交分解法 ( http: / / www.21cnjy.com ),有一个坐标轴的正方向沿着半径指向圆心.加速度沿半径方向的分量an(指向圆心)即为向心加速度,其大小为an==rω2;加速度沿轨迹切线方向的分量at即为切向加速度.
合力沿半径方向的分量Fn(或所有外 ( http: / / www.21cnjy.com )力沿半径方向分力的矢量和)提供向心力,其作用是改变速度的方向;其大小为:Fn=m=mω2r.合力沿切线方向的分力Ft(或所有外力沿切线方向的分力的矢量和)使物体产生切向加速度,其作用是改变速度的大小,其大小为Ft=mat.
3.处理匀速圆周运动问题的基本步骤
(1)确定做匀速圆周运动的物体作为研究对象.
(2)确定圆周运动的轨道平面、圆心位置和半径.
(3)对研究对象进行受力分析,作出受力示意图.
(4)运用平行四边形定则或正交分解法求出向心力Fn.
(5)根据向心力Fn=m=mω2r=mr,选择其中一种公式列方程求解.
1.传动运动
例2图中所示为一皮带传www.动装置,右轮的半径为r,a是它边缘上的一点,左侧是一轮轴,大轮的半径为4r,小轮的半径为2r,b点在小轮上,到小轮中心的距离为r,c点和d点分别位于小轮和大轮的边缘上,若在传动过程中,皮带不打滑,则( )
A.ab两点的线速度大小相www.等 B.ab两点的角速度大小相等
C.ac两点的线速度大小相等 D.ad两点的向心加速度大小相等
【解析】C选项皮带传动的两轮皮带www.接触处的线速度大小相等,C选项正确。
A选项bc角速度相等,线速度之比为1:2,所以ab线速度之比为2:1,A选项错误。
B选项ac两点的线速度大www.小相等,角速度之比为2:1,bc角速度相等,所以ab角速度之比为2:1,B选项错误。D选项,,所以D选项正确。
【答案】CD
2. 圆锥摆问题
例3有一种叫“飞椅”的游乐项目,示意图如图所示,长为L的钢绳一端系着座椅,另一端固定在半径为r的水平转盘边缘,转盘可绕穿过其中心的竖直轴转动.当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ,不计钢绳的重力,求转盘转动的角速度ω与夹角θ的关系.
( http: / / www.21cnjy.com )
【解析】设转盘转动角速度ω时,夹角为θ,座椅到中心轴的距离为
R=r+Lsinθ①
对座椅受力分析,由牛顿第二定律有
F合=mgtanθ=mRω2②
由①②两式联立得
【答案】
点评:圆锥摆是运动轨迹在水平面内的一种典型的 ( http: / / www.21cnjy.com )匀速圆周运动.其特点是由物体所受的重力与弹力的合力充当向心力,向心力的方向水平,也可以说是其中弹力的水平分力提供向心力(弹力的竖直分力和重力平衡),“飞机在水平面内做匀速圆周飞行”等在水平面内的匀速圆周运动的问题都属于此类问题.
3. 汽车过拱桥问题
例4有一辆质量为1.2t的小汽车驶上半径为50m的圆弧形拱桥。问:
①汽车到达桥顶的速度为10m/s时对桥的压力是多大?
②汽车以多大的速度经过桥顶时恰好对桥没有压力作用而腾空?
③设想拱桥的半径增www.大到与地 ( http: / / www.21cnjy.com )球半径一样,那么汽车要在这样的桥面上腾空,速度要多大?(重力加速度取10 m/s2,地球半径R取6.4×103 km)
【解析】①根据牛顿第www.二定律:
解得:,根据牛顿第三定律:
②根据牛顿第二定律:
解得:
③ 根据牛顿第二定www.律:
解得:
三、圆周运动的临界问题
[教师点拨] 4.临界问题的分析
(1)当物体从某种特性变 ( http: / / www.21cnjy.com )化为另一种特性时,发生质的飞跃的转折状态,通常叫做临界状态,出现临界状态时,既可理解为“恰好出现”,也可理解为“恰好不出现”.
(2)解决临界问题的常用方法
①极限法:把物理问题(或过程)推向极端,从而使临界现
象显露,达到尽快求解的目的.
②假设法:有些物理过程中没有明显出现临界问题的线索,但在变化过程中可能出现临界问题.
(3)关于临界问题总是出现在变速圆周运动中,而竖直平面内的圆周运动是最典型的变速圆周运动.
在竖直平面内的圆周运动一般不是匀速圆周运动,但物体经最高点或最低点时,所受的重力与其他力的合力指向圆心,提供向心力.
①
图5-3
用绳子系物体或物体沿轨道内侧运动(如图5-3所示)
此种情况下,如果物体恰能通过最高点,即 ( http: / / www.21cnjy.com )绳子的拉力或轨道对物体的支持力等于零,只有重力提供向心力,即mg=,得临界速度v0=.当物体的速度大于v0时,才能经过最高点.
②用杆固定物体在竖直平面内做圆周运动
此种情况下,由于物体所受的重力可以由杆 ( http: / / www.21cnjy.com )给它的向上的支持力来平衡,所以在最高点时的速度可以为零.当物体在最高点的速度v≥0时,物体就可以完成一个完整的圆周运
例5 在光滑平面中,有一转动轴垂直于此平面,交点O的上方h处固定一细绳的一端,绳的另一端固定一质量为m的小球B,绳长AB=l>h,小球可随转动轴转动并在光滑水平面上做匀速圆周运动,如图5-5所示,要使球不离开水平面,转动轴的转速的最大值是( )
A. B.π C. D.2π
解析 如右图所示,
以小球为研究对象,小球受三个力的作 ( http: / / www.21cnjy.com )用,重力mg、水平面支持力FN、绳子拉力F.在竖直方向合力为零,在水平方向所需向心力为,而R=htan θ,得
Fcos θ+FN=mg
Fsin θ==mω2R=m4π2n2R=m4π2n2htan θ
当球即将离开水平面时,FN=0,转速n有最大值.
FN=mg-m4π2n2h=0
n= ,故选A.
答案 A
