鲁教五四新版七年级数学上册《第3章+勾股定理》2015年单元测试卷(河南省濮阳六中)
文档属性
| 名称 | 鲁教五四新版七年级数学上册《第3章+勾股定理》2015年单元测试卷(河南省濮阳六中) | 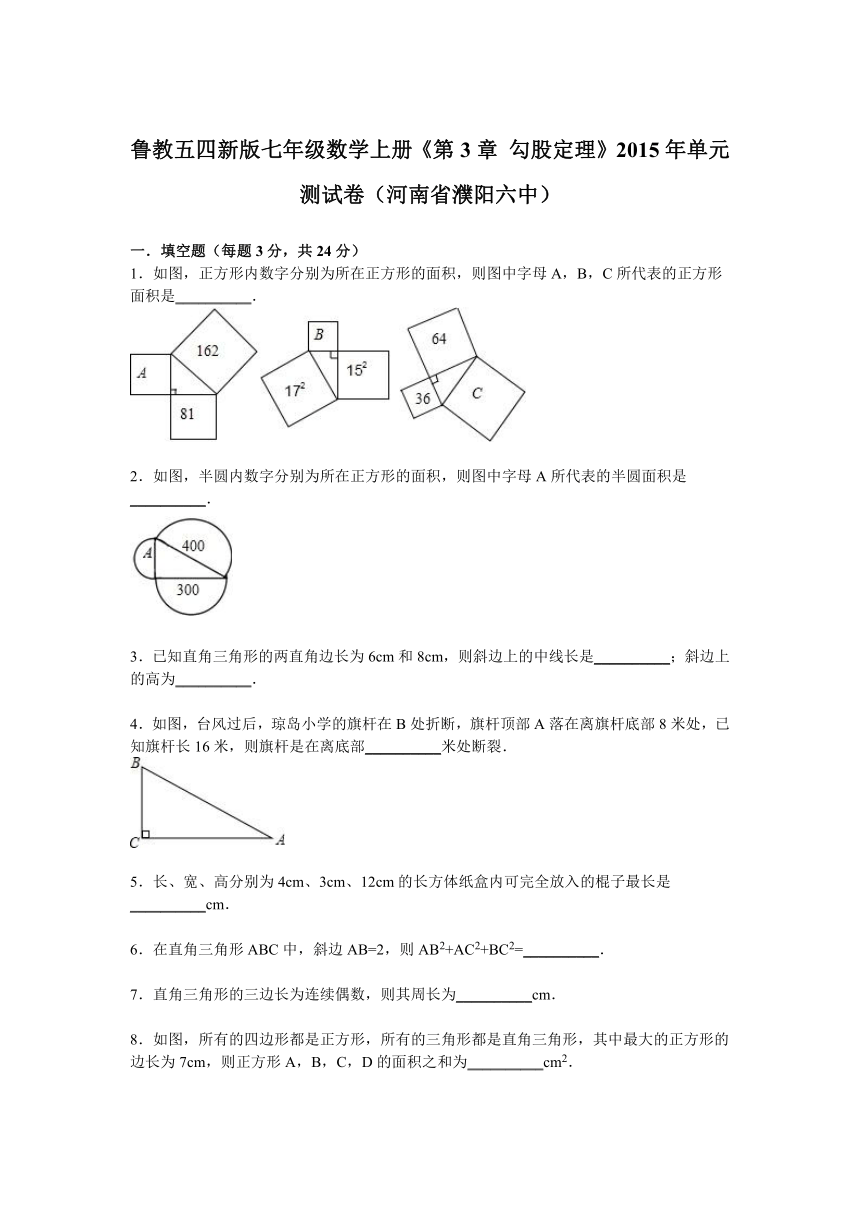 | |
| 格式 | zip | ||
| 文件大小 | 377.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-17 18:33:52 | ||
图片预览


文档简介
鲁教五四新版七年级数学上册《第3章 勾股定理》2015年单元测试卷(河南省濮阳六中)
一.填空题(每题3分,共24分)
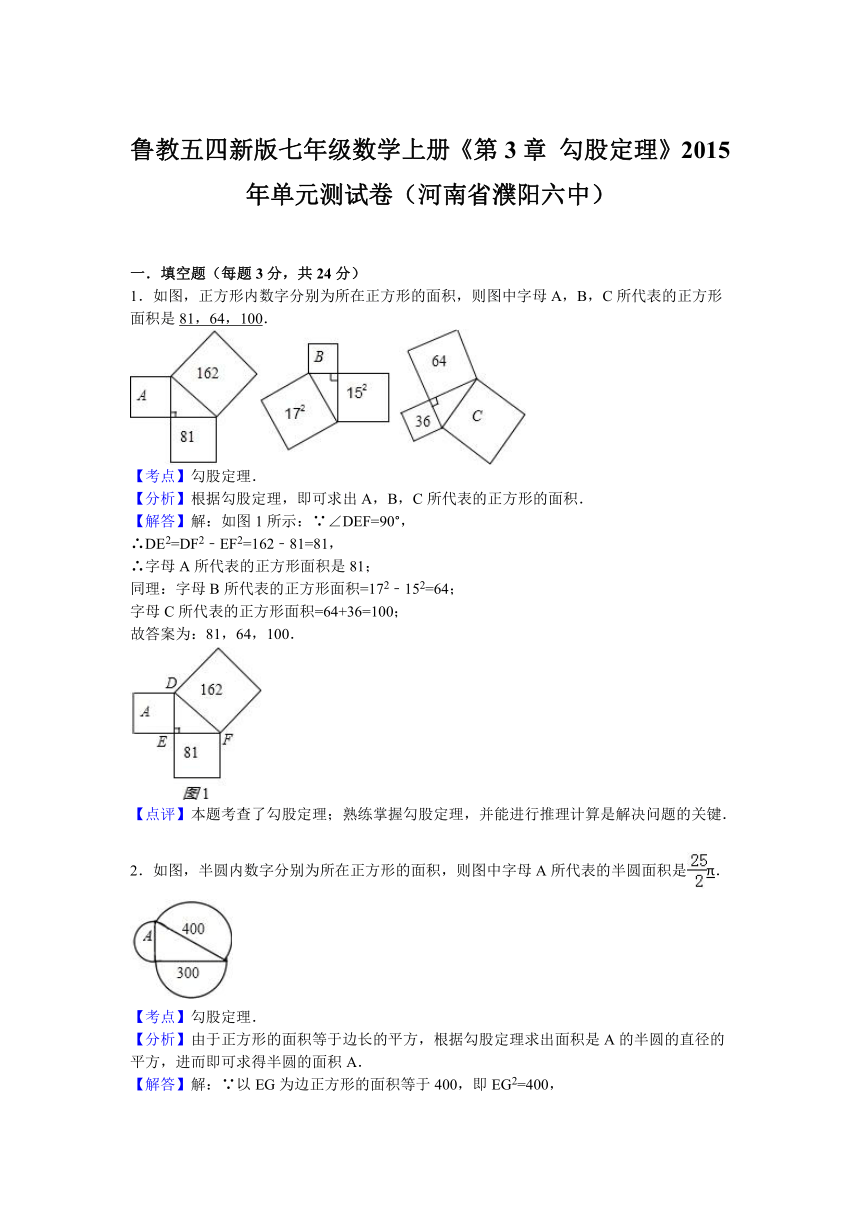
1.如图,正方形内数字分别为所在正方形的面积,则图中字母A,B,C所代表的正方形面积是__________.
( http: / / www.21cnjy.com )
2.如图,半圆内数字分别为所在正方形的面积,则图中字母A所代表的半圆面积是__________.
( http: / / www.21cnjy.com )
3.已知直角三角形的两直角边长为6cm和8cm,则斜边上的中线长是__________;斜边上的高为__________.
4.如图,台风过后,琼岛小学的旗杆在B处 ( http: / / www.21cnjy.com )折断,旗杆顶部A落在离旗杆底部8米处,已知旗杆长16米,则旗杆是在离底部__________米处断裂.
( http: / / www.21cnjy.com )
5.长、宽、高分别为4cm、3cm、12cm的长方体纸盒内可完全放入的棍子最长是__________cm.
6.在直角三角形ABC中,斜边AB=2,则AB2+AC2+BC2=__________.
7.直角三角形的三边长为连续偶数,则其周长为__________cm.
8.如图,所有的四边形都是正方形,所有的三 ( http: / / www.21cnjy.com )角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为__________cm2.
( http: / / www.21cnjy.com )
二、选择题(每题3分,共24分)
9.在Rt△ABC中,a、b、c分别是∠A、∠B、∠C、的对边,若∠A=90°,则( )
A.a2+b2=c2 B.b2+c2=a2 C.c2+a2=b2 D.b+a=c
10.观察下列几组数据:①3,4,5;②4,5,6;③6,8,10;④7,24,25.其中能作为直角三角形三边长的有( )
A.1组 B.2组 C.3组 D.4组
11.把直角三角形两直角边同时扩大到原来的2倍,则斜边扩大到原来的( )
A.2倍 B.4倍 C.3倍 D.5倍
12.一个直角三角形,两直角边长分别为3和4,下列说法正确的是( )
A.斜边长为5 B.三角形的周长为25
C.斜边长为25 D.三角形的面积为20
13.将直角三角形的三条边长同时扩大同一倍数,得到的三角形是( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等腰三角形
14.如图,一个圆桶儿,底面直径为16cm,高为18cm,则一只小虫底部点A爬到上底B处,则小虫所爬的最短路径长是(π取3)( )
( http: / / www.21cnjy.com )
A.20cm B.30cm C.40cm D.50cm
15.如图,有一块直角三角形纸片,两直角边 ( http: / / www.21cnjy.com )AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
( http: / / www.21cnjy.com )
A.2cm B.3cm C.4cm D.5cm
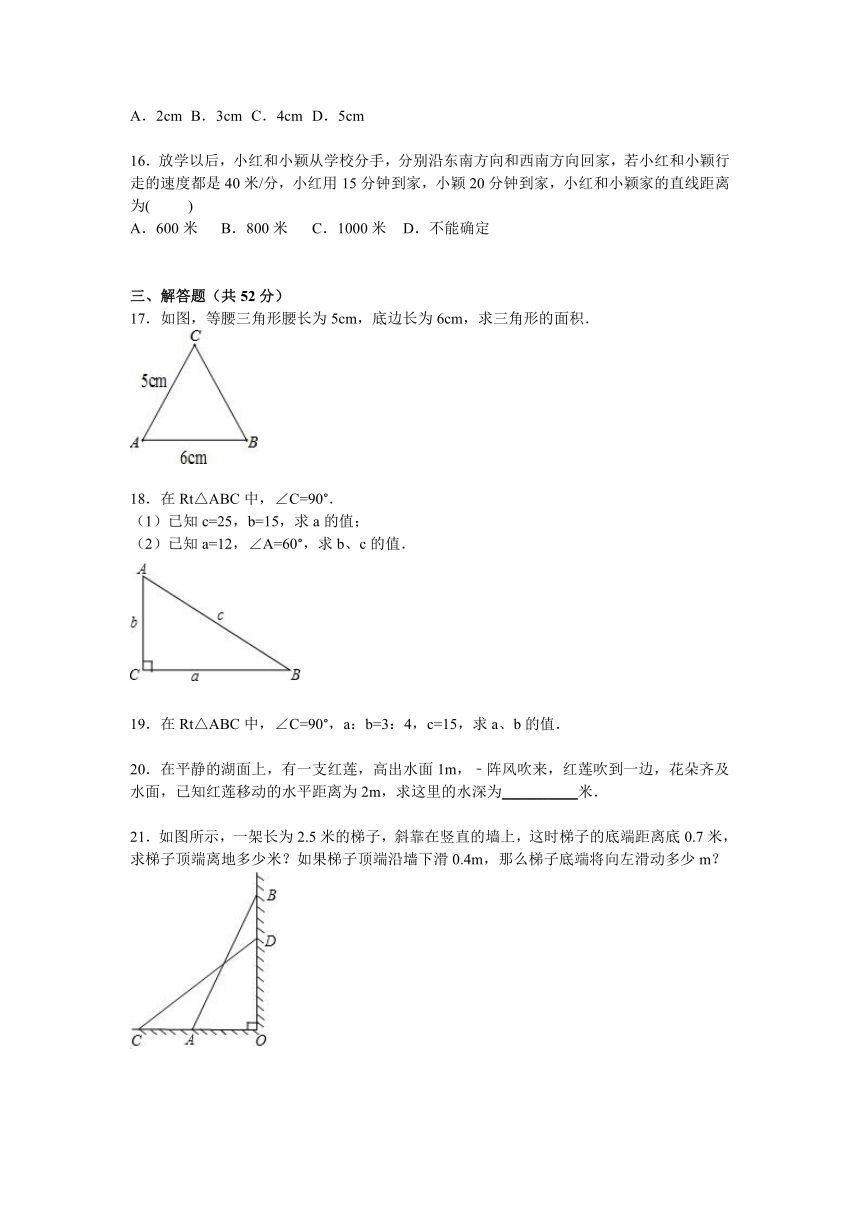
16.放学以后,小红和小颖 ( http: / / www.21cnjy.com )从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖20分钟到家,小红和小颖家的直线距离为( )
A.600米 B.800米 C.1000米 D.不能确定
三、解答题(共52分)
17.如图,等腰三角形腰长为5cm,底边长为6cm,求三角形的面积.
( http: / / www.21cnjy.com )
18.在Rt△ABC中,∠C=90°.
(1)已知c=25,b=15,求a的值;
(2)已知a=12,∠A=60°,求b、c的值.
( http: / / www.21cnjy.com )
19.在Rt△ABC中,∠C=90°,a:b=3:4,c=15,求a、b的值.
20.在平静的湖面上,有一支红莲,高出 ( http: / / www.21cnjy.com )水面1m,﹣阵风吹来,红莲吹到一边,花朵齐及水面,已知红莲移动的水平距离为2m,求这里的水深为__________米.
21.如图所示,一架长为2.5米的 ( http: / / www.21cnjy.com )梯子,斜靠在竖直的墙上,这时梯子的底端距离底0.7米,求梯子顶端离地多少米?如果梯子顶端沿墙下滑0.4m,那么梯子底端将向左滑动多少m?
( http: / / www.21cnjy.com )
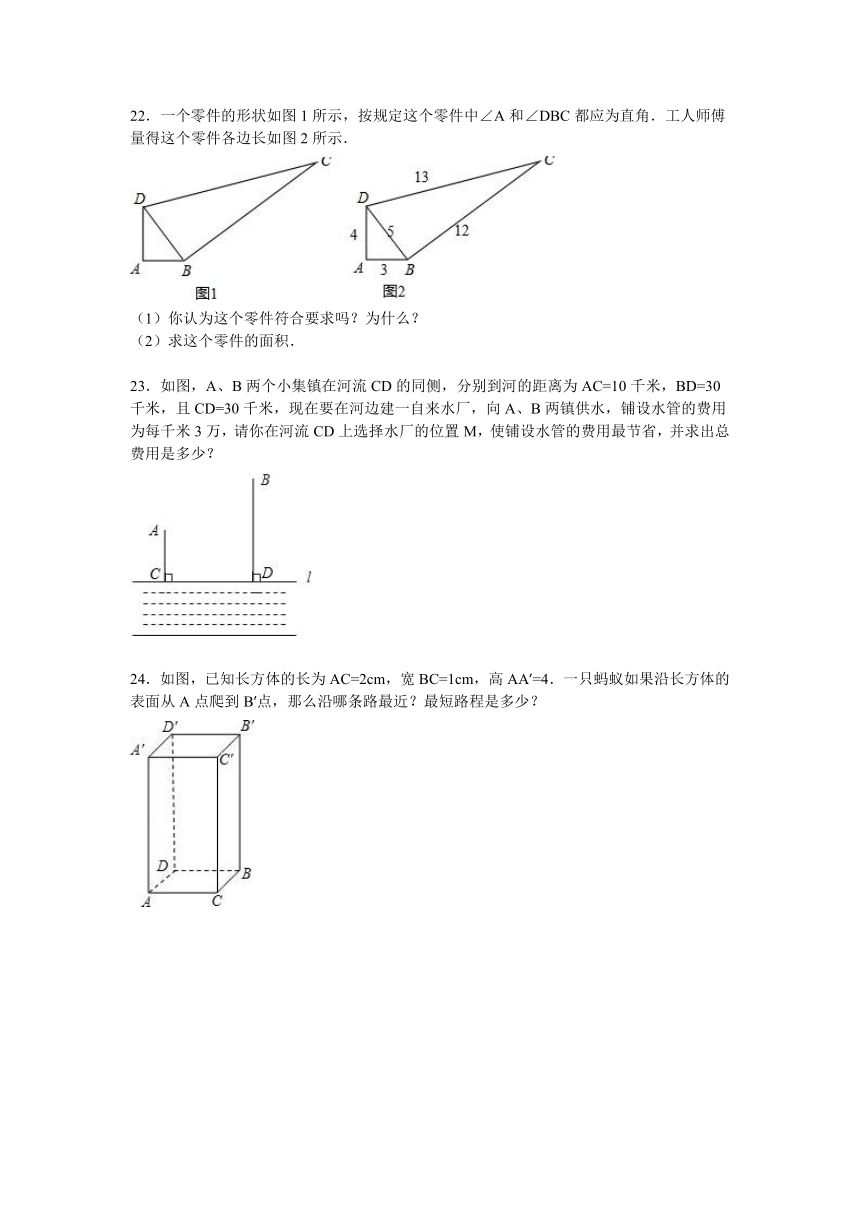
22.一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边长如图2所示.
( http: / / www.21cnjy.com )
(1)你认为这个零件符合要求吗?为什么?
(2)求这个零件的面积.
23.如图,A、B两个小集镇在河流 ( http: / / www.21cnjy.com )CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
( http: / / www.21cnjy.com )
24.如图,已知长方体的长为AC=2cm,宽 ( http: / / www.21cnjy.com )BC=1cm,高AA′=4.一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近?最短路程是多少?
( http: / / www.21cnjy.com )
鲁教五四新版七年级数学上册《第3章 勾股定理》2015年单元测试卷(河南省濮阳六中)
一.填空题(每题3分,共24分)
1.如图,正方形内数字分别为所在正方形的面积,则图中字母A,B,C所代表的正方形面积是81,64,100.
( http: / / www.21cnjy.com )
【考点】勾股定理.
【分析】根据勾股定理,即可求出A,B,C所代表的正方形的面积.
【解答】解:如图1所示:∵∠DEF=90°,
∴DE2=DF2﹣EF2=162﹣81=81,
∴字母A所代表的正方形面积是81;
同理:字母B所代表的正方形面积=172﹣152=64;
字母C所代表的正方形面积=64+36=100;
故答案为:81,64,100.
( http: / / www.21cnjy.com )
【点评】本题考查了勾股定理;熟练掌握勾股定理,并能进行推理计算是解决问题的关键.
2.如图,半圆内数字分别为所在正方形的面积,则图中字母A所代表的半圆面积是π.
( http: / / www.21cnjy.com )
【考点】勾股定理.
【分析】由于正方形的面积等于边长的平方,根据勾股定理求出面积是A的半圆的直径的平方,进而即可求得半圆的面积A.
【解答】解:∵以EG为边正方形的面积等于400,即EG2=400,
∵以FG为边正方形的面积为300,
∴FG2=300,
又∵△EFG为直角三角形,根据勾股定理得:
EG2=EF2+FG2,
∴EF2=EG2﹣FG2=400﹣300=100,
∴EF=10,
则半圆的面积为:A=π()2=π.
故答案为π.
( http: / / www.21cnjy.com )
【点评】此题考查了正方形的面积公式、圆的面积公式以及勾股定理,熟记正方形、圆的面积和勾股定理是解题的关键.
3.已知直角三角形的两直角边长为6cm和8cm,则斜边上的中线长是5cm;斜边上的高为4.8cm.
【考点】勾股定理;直角三角形斜边上的中线.
【专题】计算题.
【分析】根据勾股定理先求出斜边,依据直角三角形中斜边上的中线等于斜边的一半求出中线长,再根据面积相等求出斜边上的高.
【解答】解:直角三角形中两直角边长为6、8,
则根据勾股定理可得斜边长的平方等于两直角边的平方和,
∴斜边长==10,
∴斜边中线长=×10=5;
根据面积相等,设斜边上的高为xcm,
列方程得:×6×8=×10x,
解得x=4.8cm.
故答案为:5cm,4.8cm.
【点评】考查了勾股定理和直角三角形斜边上的中线的性质,利用面积相等来解题,是解决直角三角形问题的常用的方法,可有效简化计算.
4.如图,台风过后,琼岛小学的旗杆在B处折断,旗杆顶部A落在离旗杆底部8米处,已知旗杆长16米,则旗杆是在离底部6米处断裂.
( http: / / www.21cnjy.com )
【考点】勾股定理的应用.
【分析】旗杆折断的部分,未折断的部分和旗杆顶部离旗杆底的部分构成了直角三角形,运用勾股定理可将折断的未知求出.
【解答】解:设旗杆未折断部分长为x米,则折断部分的长为(16﹣x)m,
根据勾股定理得:x2+82=(16﹣x)2,
可得:x=6m,即距离地面6米处断裂,
故答案为:6.
【点评】本题考查了勾股定理的应用,解题的关键是建立数学模型,将实际问题运用数学思想进行求解.
5.长、宽、高分别为4cm、3cm、12cm的长方体纸盒内可完全放入的棍子最长是13cm.
【考点】勾股定理的应用.
【分析】根据题意画出图形,两次运用勾股定理即可得出结果.
【解答】解:如图所示:
BC=3cm,CD=4cm,AB=12cm,
连接BD、AD,
在Rt△BCD中,BD===5(cm),
在Rt△ABD中,AD===13(cm).
故这个盒子最长能放13cm的棍子.
故答案为:13.
( http: / / www.21cnjy.com )
【点评】本题考查的是勾股定理的应用,根据题意画出图形,作出辅助线、构造出直角三角形是解答此题的关键.
6.在直角三角形ABC中,斜边AB=2,则AB2+AC2+BC2=8.
【考点】勾股定理.
【专题】计算题.
【分析】由三角形ABC为直 ( http: / / www.21cnjy.com )角三角形,利用勾股定理根据斜边AB的长,可得出AB的平方及两直角边的平方和,然后将所求式子的后两项结合,将各自的值代入即可求出值.
【解答】解:∵△ABC为直角三角形,AB为斜边,
∴AC2+BC2=AB2,又AB=2,
∴AC2+BC2=AB2=4,
则AB2+BC2+CA2=AB2+(BC2+CA2)=4+4=8.
故答案为:8
【点评】此题考查了勾股定理的运用,勾股定理为:直角三角形中,斜边的平方等于两直角边的平方和,熟练掌握勾股定理是解本题的关键.
7.直角三角形的三边长为连续偶数,则其周长为24cm.
【考点】勾股定理.
【分析】设直角三角形的三 ( http: / / www.21cnjy.com )边边长分别为2n﹣2,2n,2n+2,由勾股定理得:两直角边的平方和等于斜边的平方,据此列出关于n的方程,求出符合题意n的值,即求出了直角三角形的三边长,之后求出周长即可.
【解答】解:设直角三角形的三边边长分别为2n﹣2,2n,2n+2.由勾股定理得:
(2n﹣2)2+(2n)2=(2n+2)2,
解得:n1=4,n2=0(不合题意舍去),
即:该直角三角形的三边边长分别为6cm,8cm,10cm.
所以,其周长为6+8+10=24cm.
【点评】本题主要考查了运用直角三角形的 ( http: / / www.21cnjy.com )性质的能力,关键在于运用勾股定理得出三边之间的关系,根据题意求出三边的边长.周长=三边之和,求出周长.
8.如图,所有的四边形都是正方形,所有 ( http: / / www.21cnjy.com )的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为49cm2.
( http: / / www.21cnjy.com )
【考点】勾股定理.
【分析】根据正方形的面积公式,连续运用勾股定理,发现:四个小正方形的面积和等于最大正方形的面积.
【解答】解:由图形可知四个小正方形的面积和等于最大正方形的面积,
故正方形A,B,C,D的面积之和=49cm2.
故答案为:49cm2.
【点评】熟练运用勾股定理进行面积的转换.
二、选择题(每题3分,共24分)
9.在Rt△ABC中,a、b、c分别是∠A、∠B、∠C、的对边,若∠A=90°,则( )
A.a2+b2=c2 B.b2+c2=a2 C.c2+a2=b2 D.b+a=c
【考点】勾股定理.
【分析】根据题意画出图形,利用勾股定理求解即可.
【解答】解:如图所示,
∵∠A=90°,
∴b2+c2=a2.
故选B.
( http: / / www.21cnjy.com )
【点评】本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
10.观察下列几组数据:①3,4,5;②4,5,6;③6,8,10;④7,24,25.其中能作为直角三角形三边长的有( )
A.1组 B.2组 C.3组 D.4组
【考点】勾股定理的逆定理.
【分析】由勾股定理的逆定理得出①③④能构成直角三角形,②不能构成直角三角形;即可得出结论.
【解答】解:∵32+42=52,
∴3,4,5能构成直角三角形,
∴①能作为直角三角形三边长;
∵42+52≠62,
∴4,5,6不能构成直角三角形,
∴②不能作为直角三角形三边长;
∵62+82=102,
∴6,8,10能构成直角三角形,
∴③能作为直角三角形三边长;
∵72+242=252,
∴7,24,25能构成直角三角形,
∴④能作为直角三角形三边长;
∴能作为直角三角形三边长的有3组,
故选:C.
【点评】本题考查了勾股定理的逆定理;熟练掌握勾股定理的逆定理,并能进行推理论证与计算是解决问题的关键.
11.把直角三角形两直角边同时扩大到原来的2倍,则斜边扩大到原来的( )
A.2倍 B.4倍 C.3倍 D.5倍
【考点】勾股定理.
【分析】根据勾股定理,可知:把直角三角形两直角边同时扩大到原来的2倍,则斜边扩大到原来的2倍.
【解答】解:设一直角三角形直角边为a、b,斜边为c.则a2+b2=c2;
另一直角三角形直角边为2a、2b,则根据勾股定理知斜边为=2c.
即直角三角形两直角边同时扩大到原来的2倍,则斜边扩大到原来的2倍.
故选A.
【点评】熟练运用勾股定理对式子进行变形.
12.一个直角三角形,两直角边长分别为3和4,下列说法正确的是( )
A.斜边长为5 B.三角形的周长为25
C.斜边长为25 D.三角形的面积为20
【考点】勾股定理.
【分析】利用勾股定理求出后直接选取答案.
【解答】解:两直角边长分别为3和4,
∴斜边==5;
故选A.
【点评】此题较简单关键是熟知勾股定理:在直角三角形中两条直角边的平方和等于斜边的平方.
13.将直角三角形的三条边长同时扩大同一倍数,得到的三角形是( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等腰三角形
【考点】相似三角形的性质.
【分析】根据三组对应边的比相等的三角形相似,依据相似三角形的性质就可以求解.
【解答】解:将直角三角形的三条边长同时扩大同一倍数,得到的三角形与原三角形相似,因而得到的三角形是直角三角形.
故选C.
【点评】本题主要考查相似三角形的判定以及性质.
14.如图,一个圆桶儿,底面直径为16cm,高为18cm,则一只小虫底部点A爬到上底B处,则小虫所爬的最短路径长是(π取3)( )
( http: / / www.21cnjy.com )
A.20cm B.30cm C.40cm D.50cm
【考点】平面展开-最短路径问题.
【分析】先将圆柱的侧面展开为一矩形,而矩形的长就是底面周长的一半,高就是圆柱的高,再根据勾股定理就可以求出其值.
【解答】解:展开圆柱的侧面如图,根据两点之间线段最短就可以得知AB最短.
由题意,得AC=3×16÷2=24,
在Rt△ABC中,由勾股定理,得
AB===30cm.
故选B.
( http: / / www.21cnjy.com )
【点评】本题考查了圆柱侧面展开图的运用,两点之间线段最短的运用,勾股定理的运用.在解答时将圆柱的侧面展开是关键.
15.如图,有一块直角三角形纸片, ( http: / / www.21cnjy.com )两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
( http: / / www.21cnjy.com )
A.2cm B.3cm C.4cm D.5cm
【考点】勾股定理.
【专题】几何图形问题.
【分析】先根据勾股定理求得AB的长,再根据折叠的性质求得AE,BE的长,从而利用勾股定理可求得CD的长.
【解答】解:∵AC=6cm,BC=8cm,∠C=90°
∴AB=10cm,
∵AE=6cm(折叠的性质),
∴BE=4cm,
设CD=x,
则在Rt△DEB中,
42+x2=(8﹣x)2,
∴x=3cm.
故选:B.
【点评】本题考查了利用勾股定理解直角三角形的能力,即:直角三角形两直角边的平方和等于斜边的平方.
16.放学以后,小红和小颖从学校分手,分 ( http: / / www.21cnjy.com )别沿东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖20分钟到家,小红和小颖家的直线距离为( )
A.600米 B.800米 C.1000米 D.不能确定
【考点】勾股定理的应用.
【分析】两人的方向分别是东南方向和西南方向,因而两人的家所在点与学校的连线正好互相垂直,根据勾股定理即可求解.
【解答】解:根据题意得:如图:
OA=40×20=800m.
OB=40×15=600m.
在直角△OAB中,AB==1000米.
故选C.
( http: / / www.21cnjy.com )
【点评】本题考查正确运用勾股定理的应用,解题时从实际问题中整理出直角三角形是本题的关键.善于观察题目的信息是解题以及学好数学的关键.
三、解答题(共52分)
17.如图,等腰三角形腰长为5cm,底边长为6cm,求三角形的面积.
( http: / / www.21cnjy.com )
【考点】勾股定理;等腰三角形的性质.
【分析】作CD⊥AB于D,则∠ADC=90°,AD=AB=3cm,由勾股定理求出CD,△ABC的面积=AB CD,即可得出结果.
【解答】解:作CD⊥AB于D,如图所示:
则∠ADC=90°,AD=AB=3cm,
∴CD===4(cm),
∴△ABC的面积=AB CD=×6×4=12(cm2).
( http: / / www.21cnjy.com )
【点评】本题考查了等腰三角形的性质、勾股定理;熟练掌握等腰三角形的性质,并能进行推理计算是解决问题的关键.
18.在Rt△ABC中,∠C=90°.
(1)已知c=25,b=15,求a的值;
(2)已知a=12,∠A=60°,求b、c的值.
( http: / / www.21cnjy.com )
【考点】勾股定理;含30度角的直角三角形.
【分析】(1)直接根据勾股定理即可得出a的值;
(2)根据锐角三角函数的定义即可得出b、c的值.
【解答】解:(1)∵Rt△ABC中,∠C=90°,c=25,b=15,
∴a===20;
(2)∵Rt△ABC中,∠C=90°,a=12,∠A=60°,
∴b=a cot60°=12×=4,c===8.
【点评】本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
19.在Rt△ABC中,∠C=90°,a:b=3:4,c=15,求a、b的值.
【考点】勾股定理.
【分析】首先设出a=3k,b=4k,然后运用勾股定理列出关于k的方程,求出k的值即可解决问题.
【解答】解:∵a:b=3:4,
∴设a=3k,b=4k;
由勾股定理得:
(3k)2+(4k)2=152,
解得:k=3,
∴a=9,b=12.
【点评】该题以直角三角形为载体,考查了勾股定理及其应用问题;灵活运用勾股定理来分析、判断是解题的关键.
20.在平静的湖面上,有一支红莲,高出水面1m,﹣阵风吹来,红莲吹到一边,花朵齐及水面,已知红莲移动的水平距离为2m,求这里的水深为米.
【考点】勾股定理的应用.
【专题】应用题.
【分析】根据题意画出图形,结合图形利用勾股定理解答.
【解答】解:如图,AD是红莲高出水面部分,即AD=1,B是红莲入泥处(根部).
设BD=x,则BA=1+x,
所以BC=AB=1+x,
在Rt△BCD中,CD2+BD2=BC2,
即22+x2=(1+x)2,
4+x2=1+2x+x2,
2x=3
∴x=.
故这里的水深m.
( http: / / www.21cnjy.com )
【点评】本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.
21.如图所示,一架长为2.5米的梯 ( http: / / www.21cnjy.com )子,斜靠在竖直的墙上,这时梯子的底端距离底0.7米,求梯子顶端离地多少米?如果梯子顶端沿墙下滑0.4m,那么梯子底端将向左滑动多少m?
( http: / / www.21cnjy.com )
【考点】勾股定理的应用.
【分析】首先利用勾股定理得出BO的长,进而求出CO的长,即可得出答案.
【解答】解:由题意可得:AB=2.5m,AO=0.7m,
故BO==2.4(m),
∵梯子顶端沿墙下滑0.4m,
∴DO=2m,CD=2.5m,
∴CO=1.5m,
∴AC=CO﹣AO=1.5﹣0.7=0.8(m).
答:梯子底端将向左滑动0.8m.
【点评】此题主要考查了勾股定理的应用,熟练利用勾股定理是解题关键.
22.一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边长如图2所示.
( http: / / www.21cnjy.com )
(1)你认为这个零件符合要求吗?为什么?
(2)求这个零件的面积.
【考点】勾股定理的逆定理;勾股定理.
【分析】(1)根据勾股定理的逆定理,判断出△ABD、△BDC的形状,从而判断这个零件是否符合要求;
(2)这个零件的面积=△ABD的面积+△BDC的面积,再根据三角形面积公式即可求解.
【解答】解:(1)∵AD=4,AB=3,BD=5,DC=13,BC=12,
∴AB2+AD2=BD2,
BD2+BC2=DC2,
∴△ABD、△BDC是直角三角形,
∴∠A=90°,∠DBC=90°,
故这个零件符合要求.
(2)这个零件的面积=△ABD的面积+△BDC的面积
=3×4÷2+5×12÷2
=6+30
=36.
故这个零件的面积是36.
【点评】本题考查了勾股定理的逆定理,关 ( http: / / www.21cnjy.com )键是根据勾股定理的逆定理判断△ABD、△BDC的形状.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
23.如图,A、B两个小集镇在 ( http: / / www.21cnjy.com )河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
( http: / / www.21cnjy.com )
【考点】轴对称-最短路线问题.
【专题】计算题;作图题.
【分析】此题的关键是确定点M的位置,需 ( http: / / www.21cnjy.com )要首先作点A的对称点A′,连接点B和点A′,交l于点M,M即所求作的点.根据轴对称的性质,知:MA+MB=A′B.根据勾股定理即可求解.
【解答】解:作A关于CD的对称点A′,连接A′B与CD,交点CD于M,点M即为所求作的点,
则可得:DK=A′C=AC=10千米,
∴BK=BD+DK=40千米,
∴AM+BM=A′B==50千米,
总费用为50×3=150万元.
( http: / / www.21cnjy.com )
【点评】此类题的重点在于能够确定点M的位置,再运用勾股定理即可求解.
24.如图,已知长方体的长为AC=2cm, ( http: / / www.21cnjy.com )宽BC=1cm,高AA′=4.一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近?最短路程是多少?
( http: / / www.21cnjy.com )
【考点】平面展开-最短路径问题.
【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.
【解答】解:如图:
( http: / / www.21cnjy.com )
根据题意,如上图所示,最短路径有以下三种情况:
(1)沿AA′,A′C′,C′B′,B′B剪开,得图(1)AB′2=AB2+BB′2=(2+1)2+42=25;
(2)沿AC,CC′,C′B′,B′D′,D′A′,A′A剪开,得图(2)AB′2=AC2+B′C2=22+(4+1)2=4+25=29;
(3)沿AD,DD′,B′D′,C′B′,C′A′,AA′剪开,得图(3)AB′2=AD2+B′D2=12+(4+2)2=1+36=37;
综上所述,最短路径应为(1)所示,所以AB′2=25,即AB′=5cm.
【点评】将长方体从不同角度展开,是解决此类问题的关键,注意不要漏解.
一.填空题(每题3分,共24分)
1.如图,正方形内数字分别为所在正方形的面积,则图中字母A,B,C所代表的正方形面积是__________.
( http: / / www.21cnjy.com )
2.如图,半圆内数字分别为所在正方形的面积,则图中字母A所代表的半圆面积是__________.
( http: / / www.21cnjy.com )
3.已知直角三角形的两直角边长为6cm和8cm,则斜边上的中线长是__________;斜边上的高为__________.
4.如图,台风过后,琼岛小学的旗杆在B处 ( http: / / www.21cnjy.com )折断,旗杆顶部A落在离旗杆底部8米处,已知旗杆长16米,则旗杆是在离底部__________米处断裂.
( http: / / www.21cnjy.com )
5.长、宽、高分别为4cm、3cm、12cm的长方体纸盒内可完全放入的棍子最长是__________cm.
6.在直角三角形ABC中,斜边AB=2,则AB2+AC2+BC2=__________.
7.直角三角形的三边长为连续偶数,则其周长为__________cm.
8.如图,所有的四边形都是正方形,所有的三 ( http: / / www.21cnjy.com )角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为__________cm2.
( http: / / www.21cnjy.com )
二、选择题(每题3分,共24分)
9.在Rt△ABC中,a、b、c分别是∠A、∠B、∠C、的对边,若∠A=90°,则( )
A.a2+b2=c2 B.b2+c2=a2 C.c2+a2=b2 D.b+a=c
10.观察下列几组数据:①3,4,5;②4,5,6;③6,8,10;④7,24,25.其中能作为直角三角形三边长的有( )
A.1组 B.2组 C.3组 D.4组
11.把直角三角形两直角边同时扩大到原来的2倍,则斜边扩大到原来的( )
A.2倍 B.4倍 C.3倍 D.5倍
12.一个直角三角形,两直角边长分别为3和4,下列说法正确的是( )
A.斜边长为5 B.三角形的周长为25
C.斜边长为25 D.三角形的面积为20
13.将直角三角形的三条边长同时扩大同一倍数,得到的三角形是( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等腰三角形
14.如图,一个圆桶儿,底面直径为16cm,高为18cm,则一只小虫底部点A爬到上底B处,则小虫所爬的最短路径长是(π取3)( )
( http: / / www.21cnjy.com )
A.20cm B.30cm C.40cm D.50cm
15.如图,有一块直角三角形纸片,两直角边 ( http: / / www.21cnjy.com )AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
( http: / / www.21cnjy.com )
A.2cm B.3cm C.4cm D.5cm
16.放学以后,小红和小颖 ( http: / / www.21cnjy.com )从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖20分钟到家,小红和小颖家的直线距离为( )
A.600米 B.800米 C.1000米 D.不能确定
三、解答题(共52分)
17.如图,等腰三角形腰长为5cm,底边长为6cm,求三角形的面积.
( http: / / www.21cnjy.com )
18.在Rt△ABC中,∠C=90°.
(1)已知c=25,b=15,求a的值;
(2)已知a=12,∠A=60°,求b、c的值.
( http: / / www.21cnjy.com )
19.在Rt△ABC中,∠C=90°,a:b=3:4,c=15,求a、b的值.
20.在平静的湖面上,有一支红莲,高出 ( http: / / www.21cnjy.com )水面1m,﹣阵风吹来,红莲吹到一边,花朵齐及水面,已知红莲移动的水平距离为2m,求这里的水深为__________米.
21.如图所示,一架长为2.5米的 ( http: / / www.21cnjy.com )梯子,斜靠在竖直的墙上,这时梯子的底端距离底0.7米,求梯子顶端离地多少米?如果梯子顶端沿墙下滑0.4m,那么梯子底端将向左滑动多少m?
( http: / / www.21cnjy.com )
22.一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边长如图2所示.
( http: / / www.21cnjy.com )
(1)你认为这个零件符合要求吗?为什么?
(2)求这个零件的面积.
23.如图,A、B两个小集镇在河流 ( http: / / www.21cnjy.com )CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
( http: / / www.21cnjy.com )
24.如图,已知长方体的长为AC=2cm,宽 ( http: / / www.21cnjy.com )BC=1cm,高AA′=4.一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近?最短路程是多少?
( http: / / www.21cnjy.com )
鲁教五四新版七年级数学上册《第3章 勾股定理》2015年单元测试卷(河南省濮阳六中)
一.填空题(每题3分,共24分)
1.如图,正方形内数字分别为所在正方形的面积,则图中字母A,B,C所代表的正方形面积是81,64,100.
( http: / / www.21cnjy.com )
【考点】勾股定理.
【分析】根据勾股定理,即可求出A,B,C所代表的正方形的面积.
【解答】解:如图1所示:∵∠DEF=90°,
∴DE2=DF2﹣EF2=162﹣81=81,
∴字母A所代表的正方形面积是81;
同理:字母B所代表的正方形面积=172﹣152=64;
字母C所代表的正方形面积=64+36=100;
故答案为:81,64,100.
( http: / / www.21cnjy.com )
【点评】本题考查了勾股定理;熟练掌握勾股定理,并能进行推理计算是解决问题的关键.
2.如图,半圆内数字分别为所在正方形的面积,则图中字母A所代表的半圆面积是π.
( http: / / www.21cnjy.com )
【考点】勾股定理.
【分析】由于正方形的面积等于边长的平方,根据勾股定理求出面积是A的半圆的直径的平方,进而即可求得半圆的面积A.
【解答】解:∵以EG为边正方形的面积等于400,即EG2=400,
∵以FG为边正方形的面积为300,
∴FG2=300,
又∵△EFG为直角三角形,根据勾股定理得:
EG2=EF2+FG2,
∴EF2=EG2﹣FG2=400﹣300=100,
∴EF=10,
则半圆的面积为:A=π()2=π.
故答案为π.
( http: / / www.21cnjy.com )
【点评】此题考查了正方形的面积公式、圆的面积公式以及勾股定理,熟记正方形、圆的面积和勾股定理是解题的关键.
3.已知直角三角形的两直角边长为6cm和8cm,则斜边上的中线长是5cm;斜边上的高为4.8cm.
【考点】勾股定理;直角三角形斜边上的中线.
【专题】计算题.
【分析】根据勾股定理先求出斜边,依据直角三角形中斜边上的中线等于斜边的一半求出中线长,再根据面积相等求出斜边上的高.
【解答】解:直角三角形中两直角边长为6、8,
则根据勾股定理可得斜边长的平方等于两直角边的平方和,
∴斜边长==10,
∴斜边中线长=×10=5;
根据面积相等,设斜边上的高为xcm,
列方程得:×6×8=×10x,
解得x=4.8cm.
故答案为:5cm,4.8cm.
【点评】考查了勾股定理和直角三角形斜边上的中线的性质,利用面积相等来解题,是解决直角三角形问题的常用的方法,可有效简化计算.
4.如图,台风过后,琼岛小学的旗杆在B处折断,旗杆顶部A落在离旗杆底部8米处,已知旗杆长16米,则旗杆是在离底部6米处断裂.
( http: / / www.21cnjy.com )
【考点】勾股定理的应用.
【分析】旗杆折断的部分,未折断的部分和旗杆顶部离旗杆底的部分构成了直角三角形,运用勾股定理可将折断的未知求出.
【解答】解:设旗杆未折断部分长为x米,则折断部分的长为(16﹣x)m,
根据勾股定理得:x2+82=(16﹣x)2,
可得:x=6m,即距离地面6米处断裂,
故答案为:6.
【点评】本题考查了勾股定理的应用,解题的关键是建立数学模型,将实际问题运用数学思想进行求解.
5.长、宽、高分别为4cm、3cm、12cm的长方体纸盒内可完全放入的棍子最长是13cm.
【考点】勾股定理的应用.
【分析】根据题意画出图形,两次运用勾股定理即可得出结果.
【解答】解:如图所示:
BC=3cm,CD=4cm,AB=12cm,
连接BD、AD,
在Rt△BCD中,BD===5(cm),
在Rt△ABD中,AD===13(cm).
故这个盒子最长能放13cm的棍子.
故答案为:13.
( http: / / www.21cnjy.com )
【点评】本题考查的是勾股定理的应用,根据题意画出图形,作出辅助线、构造出直角三角形是解答此题的关键.
6.在直角三角形ABC中,斜边AB=2,则AB2+AC2+BC2=8.
【考点】勾股定理.
【专题】计算题.
【分析】由三角形ABC为直 ( http: / / www.21cnjy.com )角三角形,利用勾股定理根据斜边AB的长,可得出AB的平方及两直角边的平方和,然后将所求式子的后两项结合,将各自的值代入即可求出值.
【解答】解:∵△ABC为直角三角形,AB为斜边,
∴AC2+BC2=AB2,又AB=2,
∴AC2+BC2=AB2=4,
则AB2+BC2+CA2=AB2+(BC2+CA2)=4+4=8.
故答案为:8
【点评】此题考查了勾股定理的运用,勾股定理为:直角三角形中,斜边的平方等于两直角边的平方和,熟练掌握勾股定理是解本题的关键.
7.直角三角形的三边长为连续偶数,则其周长为24cm.
【考点】勾股定理.
【分析】设直角三角形的三 ( http: / / www.21cnjy.com )边边长分别为2n﹣2,2n,2n+2,由勾股定理得:两直角边的平方和等于斜边的平方,据此列出关于n的方程,求出符合题意n的值,即求出了直角三角形的三边长,之后求出周长即可.
【解答】解:设直角三角形的三边边长分别为2n﹣2,2n,2n+2.由勾股定理得:
(2n﹣2)2+(2n)2=(2n+2)2,
解得:n1=4,n2=0(不合题意舍去),
即:该直角三角形的三边边长分别为6cm,8cm,10cm.
所以,其周长为6+8+10=24cm.
【点评】本题主要考查了运用直角三角形的 ( http: / / www.21cnjy.com )性质的能力,关键在于运用勾股定理得出三边之间的关系,根据题意求出三边的边长.周长=三边之和,求出周长.
8.如图,所有的四边形都是正方形,所有 ( http: / / www.21cnjy.com )的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为49cm2.
( http: / / www.21cnjy.com )
【考点】勾股定理.
【分析】根据正方形的面积公式,连续运用勾股定理,发现:四个小正方形的面积和等于最大正方形的面积.
【解答】解:由图形可知四个小正方形的面积和等于最大正方形的面积,
故正方形A,B,C,D的面积之和=49cm2.
故答案为:49cm2.
【点评】熟练运用勾股定理进行面积的转换.
二、选择题(每题3分,共24分)
9.在Rt△ABC中,a、b、c分别是∠A、∠B、∠C、的对边,若∠A=90°,则( )
A.a2+b2=c2 B.b2+c2=a2 C.c2+a2=b2 D.b+a=c
【考点】勾股定理.
【分析】根据题意画出图形,利用勾股定理求解即可.
【解答】解:如图所示,
∵∠A=90°,
∴b2+c2=a2.
故选B.
( http: / / www.21cnjy.com )
【点评】本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
10.观察下列几组数据:①3,4,5;②4,5,6;③6,8,10;④7,24,25.其中能作为直角三角形三边长的有( )
A.1组 B.2组 C.3组 D.4组
【考点】勾股定理的逆定理.
【分析】由勾股定理的逆定理得出①③④能构成直角三角形,②不能构成直角三角形;即可得出结论.
【解答】解:∵32+42=52,
∴3,4,5能构成直角三角形,
∴①能作为直角三角形三边长;
∵42+52≠62,
∴4,5,6不能构成直角三角形,
∴②不能作为直角三角形三边长;
∵62+82=102,
∴6,8,10能构成直角三角形,
∴③能作为直角三角形三边长;
∵72+242=252,
∴7,24,25能构成直角三角形,
∴④能作为直角三角形三边长;
∴能作为直角三角形三边长的有3组,
故选:C.
【点评】本题考查了勾股定理的逆定理;熟练掌握勾股定理的逆定理,并能进行推理论证与计算是解决问题的关键.
11.把直角三角形两直角边同时扩大到原来的2倍,则斜边扩大到原来的( )
A.2倍 B.4倍 C.3倍 D.5倍
【考点】勾股定理.
【分析】根据勾股定理,可知:把直角三角形两直角边同时扩大到原来的2倍,则斜边扩大到原来的2倍.
【解答】解:设一直角三角形直角边为a、b,斜边为c.则a2+b2=c2;
另一直角三角形直角边为2a、2b,则根据勾股定理知斜边为=2c.
即直角三角形两直角边同时扩大到原来的2倍,则斜边扩大到原来的2倍.
故选A.
【点评】熟练运用勾股定理对式子进行变形.
12.一个直角三角形,两直角边长分别为3和4,下列说法正确的是( )
A.斜边长为5 B.三角形的周长为25
C.斜边长为25 D.三角形的面积为20
【考点】勾股定理.
【分析】利用勾股定理求出后直接选取答案.
【解答】解:两直角边长分别为3和4,
∴斜边==5;
故选A.
【点评】此题较简单关键是熟知勾股定理:在直角三角形中两条直角边的平方和等于斜边的平方.
13.将直角三角形的三条边长同时扩大同一倍数,得到的三角形是( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等腰三角形
【考点】相似三角形的性质.
【分析】根据三组对应边的比相等的三角形相似,依据相似三角形的性质就可以求解.
【解答】解:将直角三角形的三条边长同时扩大同一倍数,得到的三角形与原三角形相似,因而得到的三角形是直角三角形.
故选C.
【点评】本题主要考查相似三角形的判定以及性质.
14.如图,一个圆桶儿,底面直径为16cm,高为18cm,则一只小虫底部点A爬到上底B处,则小虫所爬的最短路径长是(π取3)( )
( http: / / www.21cnjy.com )
A.20cm B.30cm C.40cm D.50cm
【考点】平面展开-最短路径问题.
【分析】先将圆柱的侧面展开为一矩形,而矩形的长就是底面周长的一半,高就是圆柱的高,再根据勾股定理就可以求出其值.
【解答】解:展开圆柱的侧面如图,根据两点之间线段最短就可以得知AB最短.
由题意,得AC=3×16÷2=24,
在Rt△ABC中,由勾股定理,得
AB===30cm.
故选B.
( http: / / www.21cnjy.com )
【点评】本题考查了圆柱侧面展开图的运用,两点之间线段最短的运用,勾股定理的运用.在解答时将圆柱的侧面展开是关键.
15.如图,有一块直角三角形纸片, ( http: / / www.21cnjy.com )两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
( http: / / www.21cnjy.com )
A.2cm B.3cm C.4cm D.5cm
【考点】勾股定理.
【专题】几何图形问题.
【分析】先根据勾股定理求得AB的长,再根据折叠的性质求得AE,BE的长,从而利用勾股定理可求得CD的长.
【解答】解:∵AC=6cm,BC=8cm,∠C=90°
∴AB=10cm,
∵AE=6cm(折叠的性质),
∴BE=4cm,
设CD=x,
则在Rt△DEB中,
42+x2=(8﹣x)2,
∴x=3cm.
故选:B.
【点评】本题考查了利用勾股定理解直角三角形的能力,即:直角三角形两直角边的平方和等于斜边的平方.
16.放学以后,小红和小颖从学校分手,分 ( http: / / www.21cnjy.com )别沿东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖20分钟到家,小红和小颖家的直线距离为( )
A.600米 B.800米 C.1000米 D.不能确定
【考点】勾股定理的应用.
【分析】两人的方向分别是东南方向和西南方向,因而两人的家所在点与学校的连线正好互相垂直,根据勾股定理即可求解.
【解答】解:根据题意得:如图:
OA=40×20=800m.
OB=40×15=600m.
在直角△OAB中,AB==1000米.
故选C.
( http: / / www.21cnjy.com )
【点评】本题考查正确运用勾股定理的应用,解题时从实际问题中整理出直角三角形是本题的关键.善于观察题目的信息是解题以及学好数学的关键.
三、解答题(共52分)
17.如图,等腰三角形腰长为5cm,底边长为6cm,求三角形的面积.
( http: / / www.21cnjy.com )
【考点】勾股定理;等腰三角形的性质.
【分析】作CD⊥AB于D,则∠ADC=90°,AD=AB=3cm,由勾股定理求出CD,△ABC的面积=AB CD,即可得出结果.
【解答】解:作CD⊥AB于D,如图所示:
则∠ADC=90°,AD=AB=3cm,
∴CD===4(cm),
∴△ABC的面积=AB CD=×6×4=12(cm2).
( http: / / www.21cnjy.com )
【点评】本题考查了等腰三角形的性质、勾股定理;熟练掌握等腰三角形的性质,并能进行推理计算是解决问题的关键.
18.在Rt△ABC中,∠C=90°.
(1)已知c=25,b=15,求a的值;
(2)已知a=12,∠A=60°,求b、c的值.
( http: / / www.21cnjy.com )
【考点】勾股定理;含30度角的直角三角形.
【分析】(1)直接根据勾股定理即可得出a的值;
(2)根据锐角三角函数的定义即可得出b、c的值.
【解答】解:(1)∵Rt△ABC中,∠C=90°,c=25,b=15,
∴a===20;
(2)∵Rt△ABC中,∠C=90°,a=12,∠A=60°,
∴b=a cot60°=12×=4,c===8.
【点评】本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
19.在Rt△ABC中,∠C=90°,a:b=3:4,c=15,求a、b的值.
【考点】勾股定理.
【分析】首先设出a=3k,b=4k,然后运用勾股定理列出关于k的方程,求出k的值即可解决问题.
【解答】解:∵a:b=3:4,
∴设a=3k,b=4k;
由勾股定理得:
(3k)2+(4k)2=152,
解得:k=3,
∴a=9,b=12.
【点评】该题以直角三角形为载体,考查了勾股定理及其应用问题;灵活运用勾股定理来分析、判断是解题的关键.
20.在平静的湖面上,有一支红莲,高出水面1m,﹣阵风吹来,红莲吹到一边,花朵齐及水面,已知红莲移动的水平距离为2m,求这里的水深为米.
【考点】勾股定理的应用.
【专题】应用题.
【分析】根据题意画出图形,结合图形利用勾股定理解答.
【解答】解:如图,AD是红莲高出水面部分,即AD=1,B是红莲入泥处(根部).
设BD=x,则BA=1+x,
所以BC=AB=1+x,
在Rt△BCD中,CD2+BD2=BC2,
即22+x2=(1+x)2,
4+x2=1+2x+x2,
2x=3
∴x=.
故这里的水深m.
( http: / / www.21cnjy.com )
【点评】本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.
21.如图所示,一架长为2.5米的梯 ( http: / / www.21cnjy.com )子,斜靠在竖直的墙上,这时梯子的底端距离底0.7米,求梯子顶端离地多少米?如果梯子顶端沿墙下滑0.4m,那么梯子底端将向左滑动多少m?
( http: / / www.21cnjy.com )
【考点】勾股定理的应用.
【分析】首先利用勾股定理得出BO的长,进而求出CO的长,即可得出答案.
【解答】解:由题意可得:AB=2.5m,AO=0.7m,
故BO==2.4(m),
∵梯子顶端沿墙下滑0.4m,
∴DO=2m,CD=2.5m,
∴CO=1.5m,
∴AC=CO﹣AO=1.5﹣0.7=0.8(m).
答:梯子底端将向左滑动0.8m.
【点评】此题主要考查了勾股定理的应用,熟练利用勾股定理是解题关键.
22.一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边长如图2所示.
( http: / / www.21cnjy.com )
(1)你认为这个零件符合要求吗?为什么?
(2)求这个零件的面积.
【考点】勾股定理的逆定理;勾股定理.
【分析】(1)根据勾股定理的逆定理,判断出△ABD、△BDC的形状,从而判断这个零件是否符合要求;
(2)这个零件的面积=△ABD的面积+△BDC的面积,再根据三角形面积公式即可求解.
【解答】解:(1)∵AD=4,AB=3,BD=5,DC=13,BC=12,
∴AB2+AD2=BD2,
BD2+BC2=DC2,
∴△ABD、△BDC是直角三角形,
∴∠A=90°,∠DBC=90°,
故这个零件符合要求.
(2)这个零件的面积=△ABD的面积+△BDC的面积
=3×4÷2+5×12÷2
=6+30
=36.
故这个零件的面积是36.
【点评】本题考查了勾股定理的逆定理,关 ( http: / / www.21cnjy.com )键是根据勾股定理的逆定理判断△ABD、△BDC的形状.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
23.如图,A、B两个小集镇在 ( http: / / www.21cnjy.com )河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
( http: / / www.21cnjy.com )
【考点】轴对称-最短路线问题.
【专题】计算题;作图题.
【分析】此题的关键是确定点M的位置,需 ( http: / / www.21cnjy.com )要首先作点A的对称点A′,连接点B和点A′,交l于点M,M即所求作的点.根据轴对称的性质,知:MA+MB=A′B.根据勾股定理即可求解.
【解答】解:作A关于CD的对称点A′,连接A′B与CD,交点CD于M,点M即为所求作的点,
则可得:DK=A′C=AC=10千米,
∴BK=BD+DK=40千米,
∴AM+BM=A′B==50千米,
总费用为50×3=150万元.
( http: / / www.21cnjy.com )
【点评】此类题的重点在于能够确定点M的位置,再运用勾股定理即可求解.
24.如图,已知长方体的长为AC=2cm, ( http: / / www.21cnjy.com )宽BC=1cm,高AA′=4.一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近?最短路程是多少?
( http: / / www.21cnjy.com )
【考点】平面展开-最短路径问题.
【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.
【解答】解:如图:
( http: / / www.21cnjy.com )
根据题意,如上图所示,最短路径有以下三种情况:
(1)沿AA′,A′C′,C′B′,B′B剪开,得图(1)AB′2=AB2+BB′2=(2+1)2+42=25;
(2)沿AC,CC′,C′B′,B′D′,D′A′,A′A剪开,得图(2)AB′2=AC2+B′C2=22+(4+1)2=4+25=29;
(3)沿AD,DD′,B′D′,C′B′,C′A′,AA′剪开,得图(3)AB′2=AD2+B′D2=12+(4+2)2=1+36=37;
综上所述,最短路径应为(1)所示,所以AB′2=25,即AB′=5cm.
【点评】将长方体从不同角度展开,是解决此类问题的关键,注意不要漏解.
