鲁教五四新版七年级数学上册《第6章一次函数》2015年单元测试卷(河南省濮阳六中)
文档属性
| 名称 | 鲁教五四新版七年级数学上册《第6章一次函数》2015年单元测试卷(河南省濮阳六中) |  | |
| 格式 | zip | ||
| 文件大小 | 129.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-17 18:28:41 | ||
图片预览




文档简介
鲁教五四新版七年级数学上册《第6章 一次函数》2015年单元测试卷(河南省濮阳六中)
一、填空题(每小题4分,共28分)
1.已知一个正比例函数的图象经过点(﹣2,4),则这个正比例函数的表达式是__________.
2.若函数y=﹣2xm+2是正比例函数,则m的值是__________.
3.已知一次函数y=kx+5的图象经过点(﹣1,2),则k=__________.
4.已知y与x成正比例,且当x=1时,y=2,那么当x=3时,y=__________.
5.若点P(a,b)在第二象限内,则直线y=ax+b不经过第__________象限.
6.已知点A(﹣,a),B(3,b)在函数y=﹣3x+4的象上,则a与b的大小关系是__________.
7.当__________时,一次函数y=(m+1)x+6的函数值随x的增大而减小.
二、选择题(每小题4分,共24分)
8.下列函数中,是一次函数的有( )
(1)y=πx (2)y=2x﹣1 (3)y= (4)y=2﹣3x (5)y=x2﹣1.
A.4个 B.3个 C.2个 D.1个
9.下面哪个点不在函数y=﹣2x+3的图象上( )
A.(﹣5,13) B.(0.5,2) C.(3,0) D.(1,1)
10.直线y=kx+b在坐标系中的位置如图,则( )
( http: / / www.21cnjy.com )
A. B. C. D.
11.下列一次函数中,y随x增大而减小的是( )
A.y=3x B.y=3x﹣2 C.y=3x+2x D.y=﹣3x﹣2
12.下列语句不正确的是( )
A.所有的正比例函数肯定是一次函数
B.一次函数的一般形式是y=kx+b
C.正比例函数和一次函数的图象都是直线
D.正比例函数的图象是一条过原点的直线
13.直线y=ax+b(a<0,b>0)不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
三、解答题(共48分)
14.已知一个正比例函数和一个一次函数的图象相交于点A(1,4),且一次函数的图象与x轴交于点B(3,0)
(1)求这两个函数的解析式;
(2)画出它们的图象.
15.已知y﹣2与x成正比,且当x=1时,y=﹣6
(1)求y与x之间的函数关系式;
(2)若点(a,2)在这个函数图象上,求a.
16.已知一次函数y=kx+b的图象经过点(﹣1,﹣5),且与正比例函数y=x的图象相交于点(2,a),求:
(1)a的值;
(2)k,b的值;
(3)这两个函数图象与x轴所围成的三角形的面积.
17.某市自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费1.8元,超计划部分每吨按2.0元收费.
(1)写出该单位水费y(元)与每月用水量x(吨)之间的函数关系式:
①当用水量小于等于3000吨时:__________;②当用水量大于3000吨时:__________.
(2)某月该单位用水3200吨,水费是__________ 元;若用水2800吨,水费__________ 元.
(3)若某月该单位缴纳水费9400元,则该单位用水多少吨?
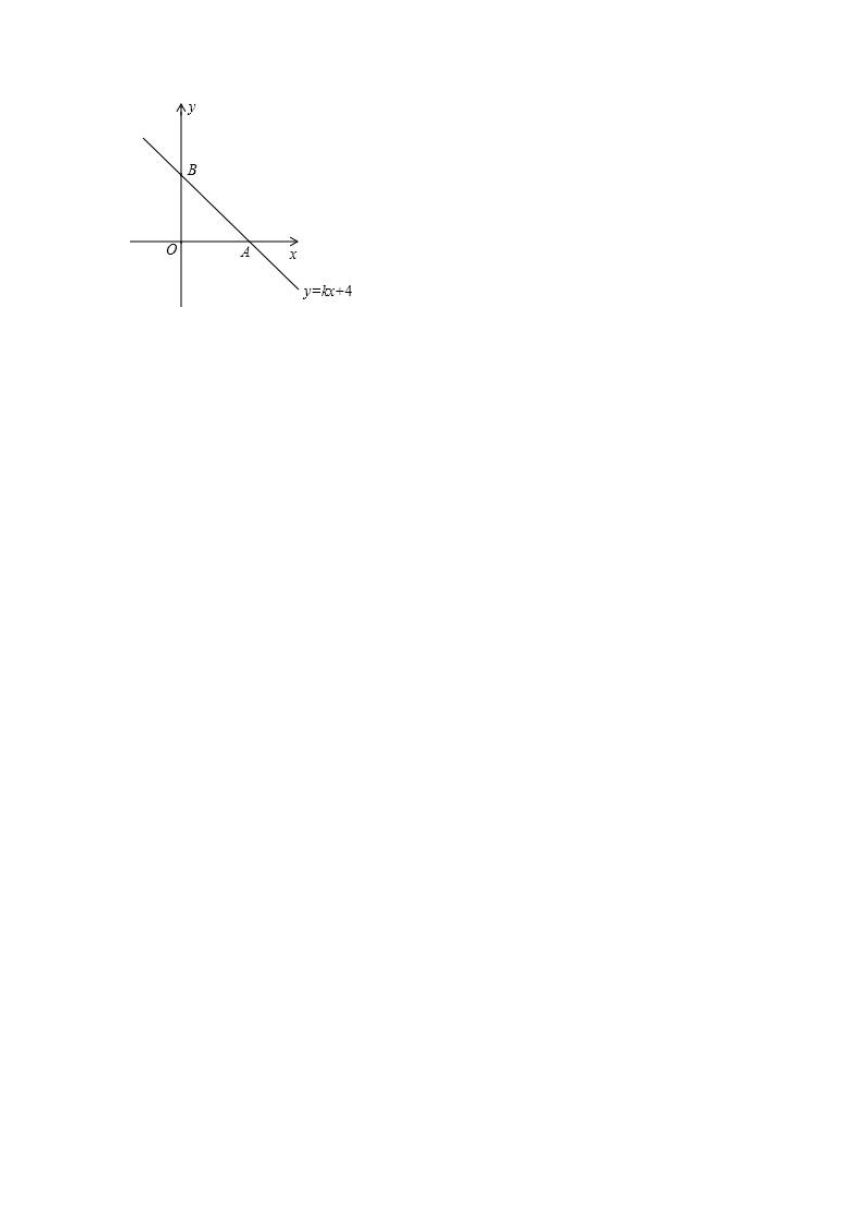
18.如图,在直角坐标系中,直线y=kx+4与x轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,求这条直线的解析式.
( http: / / www.21cnjy.com )
鲁教五四新版七年级数学上册《第6章 一次函数》2015年单元测试卷(河南省濮阳六中)
一、填空题(每小题4分,共28分)
1.已知一个正比例函数的图象经过点(﹣2,4),则这个正比例函数的表达式是y=﹣2x.
【考点】待定系数法求正比例函数解析式.
【分析】本题可设该正比例函数的解析式为y=kx,然后根据该函数图象过点(﹣2,4),由此可利用方程求出k的值,进而解决问题.
【解答】解:设该正比例函数的解析式为y=kx,根据题意,得
﹣2k=4,
k=﹣2.
则这个正比例函数的表达式是y=﹣2x.
故答案为y=﹣2x.
【点评】此类题目需灵活运用待定系数法建立函数解析式,然后将点的坐标代入解析式,利用方程解决问题.
2.若函数y=﹣2xm+2是正比例函数,则m的值是﹣1.
【考点】正比例函数的定义.
【专题】函数思想.
【分析】根据正比例函数的定义,令m+2=1,解关于m的方程即可.
【解答】解:根据题意,得
m+2=1,解得,m=﹣1;
故答案是:﹣1.
【点评】本题考查了正比例函数的定义.正比例函数y=kx的定义条件是:k为常数且k≠0,自变量次数为1.
3.已知一次函数y=kx+5的图象经过点(﹣1,2),则k=3.
【考点】一次函数图象上点的坐标特征.
【分析】直接把点(﹣1,2)代入一次函数y=kx+5,求出k的值即可.
【解答】解:∵一次函数y=kx+5的图象经过点(﹣1,2),
∴2=﹣k+5,解得k=3.
故答案为:3.
【点评】本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.
4.已知y与x成正比例,且当x=1时,y=2,那么当x=3时,y=6.
【考点】待定系数法求正比例函数解析式.
【专题】待定系数法.
【分析】用待定系数法求正比例函数的解析式.
【解答】解:因为y与x成正比例,所以设正比例函数的解析式为y=kx(k≠0),
把x=1时,y=2代入得:k=2,
故此正比例函数的解析式为:y=2x,
当x=3时,y=2×3=6.
故答案为:6.
【点评】本题考查的是用待定系数法求正比例函数的解析式,比较简单.
5.若点P(a,b)在第二象限内,则直线y=ax+b不经过第三象限.
【考点】一次函数图象与系数的关系;点的坐标.
【分析】点在第二象限的条件是:横坐标是负数,纵坐标是正数,进而判断相应的直线经过的象限.
【解答】解:∵点P(a,b)在第二象限内,
∴a<0,b>0,
∴直线y=ax+b经过第一二四象限.
∴不经过第三象限.
故答案为:三.
【点评】解决本题的关键是掌握好四个象限的点的坐标的特征:第一象限正正,第二象限负正,第三象限负负,第四象限正负;直线经过象限的特征.
6.已知点A(﹣,a),B(3,b)在函数y=﹣3x+4的象上,则a与b的大小关系是a>b.
【考点】一次函数图象上点的坐标特征.
【分析】根据k<0,y随x的增大而减小解答.
【解答】解:∵k=﹣3<0,
∴y随x的增大而减小,
∵﹣<3,
∴a>b.
故答案为:a>b.
【点评】本题考查了一次函数图象上点的坐标特征,利用一次函数的增减性求解更简便.
7.当m<﹣1时,一次函数y=(m+1)x+6的函数值随x的增大而减小.
【考点】一次函数图象与系数的关系.
【分析】直接利用一次函数的性质得出m+1<0,进而求出即可.
【解答】解:∵一次函数y=(m+1)x+6的函数值随x的增大而减小,
∴m+1<0,
解得:m<﹣1.
故答案为:m<﹣1.
【点评】此题主要考查了一次函数的性质,正确记忆一次函数增减性是解题关键.
二、选择题(每小题4分,共24分)
8.下列函数中,是一次函数的有( )
(1)y=πx (2)y=2x﹣1 (3)y= (4)y=2﹣3x (5)y=x2﹣1.
A.4个 B.3个 C.2个 D.1个
【考点】一次函数的定义.
【分析】根据一次函数的定义对各选项进行逐一分析即可.
【解答】解:(1)y=πx是一次函数;
(2)y=2x﹣1是一次函数;
(3)y=是反比例函数,不是一次函数;
(4)y=2﹣3x是一次函数;
(5)y=x2﹣1是二次函数,不是一次函数.
是一次函数的有3个.
故选:B.
【点评】本题考查的是一次函数的定义,即一般地,形如y=kx+b(k≠0,k、b是常数)的函数,叫做一次函数.
9.下面哪个点不在函数y=﹣2x+3的图象上( )
A.(﹣5,13) B.(0.5,2) C.(3,0) D.(1,1)
【考点】一次函数图象上点的坐标特征.
【专题】计算题.
【分析】把每个选项中点的横坐标代入函数解析式,判断纵坐标是否相符.
【解答】解:A、当x=﹣5时,y=﹣2x+3=13,点在函数图象上;
B、当x=0.5时,y=﹣2x+3=2,点在函数图象上;
C、当x=3时,y=﹣2x+3=﹣3,点不在函数图象上;
D、当x=1时,y=﹣2x+3=1,点在函数图象上;
故选C.
【点评】本题考查了点的坐标与函数解析式的关系,当点的横纵坐标满足函数解析式时,点在函数图象上.
10.直线y=kx+b在坐标系中的位置如图,则( )
( http: / / www.21cnjy.com )
A. B. C. D.
【考点】待定系数法求一次函数解析式.
【专题】数形结合.
【分析】由图形可得函数图象过点(2,0)和(0,1),设函数解析式为y=kx+b,运用待定系数法可求出k和b的值.
【解答】解:设函数解析式为y=kx+b,
由图形可得函数图象过点(2,0)和(0,1),
将这两点代入得:,
解得:.
故选B.
【点评】本题考查待定系数法求函数解析式,难度不大,注意数形结合的运用.
11.下列一次函数中,y随x增大而减小的是( )
A.y=3x B.y=3x﹣2 C.y=3x+2x D.y=﹣3x﹣2
【考点】一次函数的性质;正比例函数的性质.
【分析】由一次函数的性质,在直线y=kx+b(k≠0)中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
【解答】解:在y=kx+b中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
A、函数y=3x中的k=3>0,故y的值随着x值的增大而增大.故本选项错误;
B、函数y=3x﹣2中的k=3>0,y的值随着x值的增大而增大.故本选项错误;
C、函数y=3x+2x=5x中的k=5>0,y的值随着x值的增大而增大.故本选项错误;
D、函数y=﹣3x﹣2中的k=﹣3<0,y的值随着x值的增大而减小.故本选项正确;
故选D.
【点评】本题考查了一次函数的性质,属于基 ( http: / / www.21cnjy.com )础题,关键是掌握在直线y=kx+b中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
12.下列语句不正确的是( )
A.所有的正比例函数肯定是一次函数
B.一次函数的一般形式是y=kx+b
C.正比例函数和一次函数的图象都是直线
D.正比例函数的图象是一条过原点的直线
【考点】一次函数的定义;正比例函数的定义.
【分析】分别利用一次函数和反比例函数的定义以及其性质分析得出即可.
【解答】解:A、所有的正比例函数肯定是一次函数,正确,不合题意;
B、一次函数的一般形式是y=kx+b(k≠0),故此选项错误,符合题意;
C、正比例函数和一次函数的图象都是直线,正确,不合题意;
D、正比例函数的图象是一条过原点的直线,正确,不合题意;
故选:B.
【点评】此题主要考查了一次函数和反比例函数的定义,正确把握其性质是解题关键.
13.直线y=ax+b(a<0,b>0)不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】一次函数图象与系数的关系.
【专题】存在型.
【分析】先根据一次函数的图象与系数的关系得出直线y=ax+b(a<0,b>0)所经过的象限,故可得出结论.
【解答】解:∵直线y=ax+b中,a<0,b>0,
∴直线y=ax+b经过一、二、四象限,
∴不经过第三象限.
故选C.
【点评】本题考查的是一次函数的图象与系数的关系,即一次函数y=kx+b(k≠0)中,当k<0,b>0时函数的图象经过一、二、四象限.
三、解答题(共48分)
14.已知一个正比例函数和一个一次函数的图象相交于点A(1,4),且一次函数的图象与x轴交于点B(3,0)
(1)求这两个函数的解析式;
(2)画出它们的图象.
【考点】两条直线相交或平行问题.
【专题】计算题.
【分析】(1)利用待定系数法求两个函数解析式;
(2)利用描点法画出两函数图象.
【解答】解:(1)设正比例函数解析式为y=kx,
把A(1,4)代入得k=4,
所以正比例函数解析式为y=4x;
设一次函数解析式为y=ax+b,
把A(1,4),B(3,0)代入得,
解得,
所以一次函数解析式为y=﹣2x+6;
(2)如图:
( http: / / www.21cnjy.com )
【点评】本题考查了两条直线相交或平行问题: ( http: / / www.21cnjy.com )若直线y=k1x+b1与直线y=k2x+b2平行,则k1=k2;若直线y=k1x+b1与直线y=k2x+b2相交,则由两解析式所组成的方程组的解为交点坐标.也考查了待定系数法求函数解析式.
15.已知y﹣2与x成正比,且当x=1时,y=﹣6
(1)求y与x之间的函数关系式;
(2)若点(a,2)在这个函数图象上,求a.
【考点】待定系数法求一次函数解析式;一次函数图象上点的坐标特征.
【分析】(1)首先设 y﹣2=kx,再把x=1,y=6代入所设的关系式,即可算出k的值,进而得到y与x之间的函数关系式;
(2)把(a,2)代入(1)中所求的关系式即可得到a的值.
【解答】解:(1)设 y﹣2=kx
∵当x=1时,y=﹣6,
∴k=﹣6﹣2,
∴k=﹣8,
∴y与x之间的函数关系式为y﹣2=﹣8x,即y=﹣8x+2.
(2)∵点(a,2)在这个函数图象上,
∴﹣8a+2=2,
∴a=0.
【点评】此题主要考查了待定系数法求一次函数关系式,关键是掌握凡是图象经过的点必能满足解析式.
16.已知一次函数y=kx+b的图象经过点(﹣1,﹣5),且与正比例函数y=x的图象相交于点(2,a),求:
(1)a的值;
(2)k,b的值;
(3)这两个函数图象与x轴所围成的三角形的面积.
【考点】两条直线相交或平行问题.
【专题】计算题;待定系数法.
【分析】(1)由题知,点(2,a)在正比例函数图象上,代入即可求得a的值.
(2)把点(﹣1,﹣5)及点(2,a)代入一次函数解析式,再根据(1)即可求得k,b的值.
(3)由于正比例函数过原点,又有两个函数交点,求面积只需知道一次函数与x轴的交点即可,S=×a×x.
【解答】解:(1)由题知,把(2,a)代入y=x,
解得a=1;
(2)由题意知,把点(﹣1,﹣5)及点(2,a)代入一次函数解析式得:﹣k+b=﹣5,2k+b=a,
又由(1)知a=1,
解方程组得到:k=2,b=﹣3;
(3)由(2)知一次函数解析式为:y=2x﹣3,
y=2x﹣3与x轴交点坐标为(,0)
∴所求三角形面积S=×1×=;
【点评】本题考查了一次函数图象上点的坐标的性质以及正比例函数图象上点的坐标的性质,是基础题型.
17.某市自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费1.8元,超计划部分每吨按2.0元收费.
(1)写出该单位水费y(元)与每月用水量x(吨)之间的函数关系式:
①当用水量小于等于3000吨时:y=1.8x;②当用水量大于3000吨时:y=2x﹣600.
(2)某月该单位用水3200吨,水费是5800 元;若用水2800吨,水费3240 元.
(3)若某月该单位缴纳水费9400元,则该单位用水多少吨?
【考点】一次函数的应用.
【分析】(1)是个分段函数分①当用水量小于等于3000吨时和②当用水量大于3000吨时.
(2)根据给的用水量,然后代入函数值求解.
(3)代入y=9400,从而可求出x的值.
【解答】解:(1)单位水费y(元)和每月用水量x(吨),
当x≤3000吨时;y=1.8x.
当x>3000吨时:y=3000×1.8+2.0(x﹣3000)=2x﹣600.
(2)单位用水3200吨,水费是:y=2×3200﹣600=5800(元).
若用水2800吨,水费:y=1.8×2800=3240(元).
(3)当该单位缴纳水费9400元,则
9400=2x﹣600,
x=5000.
故此时用水5000吨.
【点评】本题考查一次函数的应用,关键是知道是分段函数,且用水量和钱数之间的关系,从而求解.
18.如图,在直角坐标系中,直线y=kx+4与x轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,求这条直线的解析式.
( http: / / www.21cnjy.com )
【考点】待定系数法求一次函数解析式.
【专题】计算题.
【分析】先根据坐标轴上点的坐标特征得到A(﹣,0),B(0,4),再根据三角形面积公式得到 (﹣) 4=10,然后解方程求出k的值即可得到直线解析式.
【解答】解:当y=0时,kx+4=0,解得x=﹣,则A(﹣,0),
当x=0时,y=kx+4=4,则B(0,4),
因为△OAB的面积为10,
所以 (﹣) 4=10,解得k=﹣,
所以直线解析式为y=﹣x+4.
【点评】本题考查了待定系数法求一次函数解析 ( http: / / www.21cnjy.com )式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.
一、填空题(每小题4分,共28分)
1.已知一个正比例函数的图象经过点(﹣2,4),则这个正比例函数的表达式是__________.
2.若函数y=﹣2xm+2是正比例函数,则m的值是__________.
3.已知一次函数y=kx+5的图象经过点(﹣1,2),则k=__________.
4.已知y与x成正比例,且当x=1时,y=2,那么当x=3时,y=__________.
5.若点P(a,b)在第二象限内,则直线y=ax+b不经过第__________象限.
6.已知点A(﹣,a),B(3,b)在函数y=﹣3x+4的象上,则a与b的大小关系是__________.
7.当__________时,一次函数y=(m+1)x+6的函数值随x的增大而减小.
二、选择题(每小题4分,共24分)
8.下列函数中,是一次函数的有( )
(1)y=πx (2)y=2x﹣1 (3)y= (4)y=2﹣3x (5)y=x2﹣1.
A.4个 B.3个 C.2个 D.1个
9.下面哪个点不在函数y=﹣2x+3的图象上( )
A.(﹣5,13) B.(0.5,2) C.(3,0) D.(1,1)
10.直线y=kx+b在坐标系中的位置如图,则( )
( http: / / www.21cnjy.com )
A. B. C. D.
11.下列一次函数中,y随x增大而减小的是( )
A.y=3x B.y=3x﹣2 C.y=3x+2x D.y=﹣3x﹣2
12.下列语句不正确的是( )
A.所有的正比例函数肯定是一次函数
B.一次函数的一般形式是y=kx+b
C.正比例函数和一次函数的图象都是直线
D.正比例函数的图象是一条过原点的直线
13.直线y=ax+b(a<0,b>0)不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
三、解答题(共48分)
14.已知一个正比例函数和一个一次函数的图象相交于点A(1,4),且一次函数的图象与x轴交于点B(3,0)
(1)求这两个函数的解析式;
(2)画出它们的图象.
15.已知y﹣2与x成正比,且当x=1时,y=﹣6
(1)求y与x之间的函数关系式;
(2)若点(a,2)在这个函数图象上,求a.
16.已知一次函数y=kx+b的图象经过点(﹣1,﹣5),且与正比例函数y=x的图象相交于点(2,a),求:
(1)a的值;
(2)k,b的值;
(3)这两个函数图象与x轴所围成的三角形的面积.
17.某市自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费1.8元,超计划部分每吨按2.0元收费.
(1)写出该单位水费y(元)与每月用水量x(吨)之间的函数关系式:
①当用水量小于等于3000吨时:__________;②当用水量大于3000吨时:__________.
(2)某月该单位用水3200吨,水费是__________ 元;若用水2800吨,水费__________ 元.
(3)若某月该单位缴纳水费9400元,则该单位用水多少吨?
18.如图,在直角坐标系中,直线y=kx+4与x轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,求这条直线的解析式.
( http: / / www.21cnjy.com )
鲁教五四新版七年级数学上册《第6章 一次函数》2015年单元测试卷(河南省濮阳六中)
一、填空题(每小题4分,共28分)
1.已知一个正比例函数的图象经过点(﹣2,4),则这个正比例函数的表达式是y=﹣2x.
【考点】待定系数法求正比例函数解析式.
【分析】本题可设该正比例函数的解析式为y=kx,然后根据该函数图象过点(﹣2,4),由此可利用方程求出k的值,进而解决问题.
【解答】解:设该正比例函数的解析式为y=kx,根据题意,得
﹣2k=4,
k=﹣2.
则这个正比例函数的表达式是y=﹣2x.
故答案为y=﹣2x.
【点评】此类题目需灵活运用待定系数法建立函数解析式,然后将点的坐标代入解析式,利用方程解决问题.
2.若函数y=﹣2xm+2是正比例函数,则m的值是﹣1.
【考点】正比例函数的定义.
【专题】函数思想.
【分析】根据正比例函数的定义,令m+2=1,解关于m的方程即可.
【解答】解:根据题意,得
m+2=1,解得,m=﹣1;
故答案是:﹣1.
【点评】本题考查了正比例函数的定义.正比例函数y=kx的定义条件是:k为常数且k≠0,自变量次数为1.
3.已知一次函数y=kx+5的图象经过点(﹣1,2),则k=3.
【考点】一次函数图象上点的坐标特征.
【分析】直接把点(﹣1,2)代入一次函数y=kx+5,求出k的值即可.
【解答】解:∵一次函数y=kx+5的图象经过点(﹣1,2),
∴2=﹣k+5,解得k=3.
故答案为:3.
【点评】本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.
4.已知y与x成正比例,且当x=1时,y=2,那么当x=3时,y=6.
【考点】待定系数法求正比例函数解析式.
【专题】待定系数法.
【分析】用待定系数法求正比例函数的解析式.
【解答】解:因为y与x成正比例,所以设正比例函数的解析式为y=kx(k≠0),
把x=1时,y=2代入得:k=2,
故此正比例函数的解析式为:y=2x,
当x=3时,y=2×3=6.
故答案为:6.
【点评】本题考查的是用待定系数法求正比例函数的解析式,比较简单.
5.若点P(a,b)在第二象限内,则直线y=ax+b不经过第三象限.
【考点】一次函数图象与系数的关系;点的坐标.
【分析】点在第二象限的条件是:横坐标是负数,纵坐标是正数,进而判断相应的直线经过的象限.
【解答】解:∵点P(a,b)在第二象限内,
∴a<0,b>0,
∴直线y=ax+b经过第一二四象限.
∴不经过第三象限.
故答案为:三.
【点评】解决本题的关键是掌握好四个象限的点的坐标的特征:第一象限正正,第二象限负正,第三象限负负,第四象限正负;直线经过象限的特征.
6.已知点A(﹣,a),B(3,b)在函数y=﹣3x+4的象上,则a与b的大小关系是a>b.
【考点】一次函数图象上点的坐标特征.
【分析】根据k<0,y随x的增大而减小解答.
【解答】解:∵k=﹣3<0,
∴y随x的增大而减小,
∵﹣<3,
∴a>b.
故答案为:a>b.
【点评】本题考查了一次函数图象上点的坐标特征,利用一次函数的增减性求解更简便.
7.当m<﹣1时,一次函数y=(m+1)x+6的函数值随x的增大而减小.
【考点】一次函数图象与系数的关系.
【分析】直接利用一次函数的性质得出m+1<0,进而求出即可.
【解答】解:∵一次函数y=(m+1)x+6的函数值随x的增大而减小,
∴m+1<0,
解得:m<﹣1.
故答案为:m<﹣1.
【点评】此题主要考查了一次函数的性质,正确记忆一次函数增减性是解题关键.
二、选择题(每小题4分,共24分)
8.下列函数中,是一次函数的有( )
(1)y=πx (2)y=2x﹣1 (3)y= (4)y=2﹣3x (5)y=x2﹣1.
A.4个 B.3个 C.2个 D.1个
【考点】一次函数的定义.
【分析】根据一次函数的定义对各选项进行逐一分析即可.
【解答】解:(1)y=πx是一次函数;
(2)y=2x﹣1是一次函数;
(3)y=是反比例函数,不是一次函数;
(4)y=2﹣3x是一次函数;
(5)y=x2﹣1是二次函数,不是一次函数.
是一次函数的有3个.
故选:B.
【点评】本题考查的是一次函数的定义,即一般地,形如y=kx+b(k≠0,k、b是常数)的函数,叫做一次函数.
9.下面哪个点不在函数y=﹣2x+3的图象上( )
A.(﹣5,13) B.(0.5,2) C.(3,0) D.(1,1)
【考点】一次函数图象上点的坐标特征.
【专题】计算题.
【分析】把每个选项中点的横坐标代入函数解析式,判断纵坐标是否相符.
【解答】解:A、当x=﹣5时,y=﹣2x+3=13,点在函数图象上;
B、当x=0.5时,y=﹣2x+3=2,点在函数图象上;
C、当x=3时,y=﹣2x+3=﹣3,点不在函数图象上;
D、当x=1时,y=﹣2x+3=1,点在函数图象上;
故选C.
【点评】本题考查了点的坐标与函数解析式的关系,当点的横纵坐标满足函数解析式时,点在函数图象上.
10.直线y=kx+b在坐标系中的位置如图,则( )
( http: / / www.21cnjy.com )
A. B. C. D.
【考点】待定系数法求一次函数解析式.
【专题】数形结合.
【分析】由图形可得函数图象过点(2,0)和(0,1),设函数解析式为y=kx+b,运用待定系数法可求出k和b的值.
【解答】解:设函数解析式为y=kx+b,
由图形可得函数图象过点(2,0)和(0,1),
将这两点代入得:,
解得:.
故选B.
【点评】本题考查待定系数法求函数解析式,难度不大,注意数形结合的运用.
11.下列一次函数中,y随x增大而减小的是( )
A.y=3x B.y=3x﹣2 C.y=3x+2x D.y=﹣3x﹣2
【考点】一次函数的性质;正比例函数的性质.
【分析】由一次函数的性质,在直线y=kx+b(k≠0)中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
【解答】解:在y=kx+b中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
A、函数y=3x中的k=3>0,故y的值随着x值的增大而增大.故本选项错误;
B、函数y=3x﹣2中的k=3>0,y的值随着x值的增大而增大.故本选项错误;
C、函数y=3x+2x=5x中的k=5>0,y的值随着x值的增大而增大.故本选项错误;
D、函数y=﹣3x﹣2中的k=﹣3<0,y的值随着x值的增大而减小.故本选项正确;
故选D.
【点评】本题考查了一次函数的性质,属于基 ( http: / / www.21cnjy.com )础题,关键是掌握在直线y=kx+b中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
12.下列语句不正确的是( )
A.所有的正比例函数肯定是一次函数
B.一次函数的一般形式是y=kx+b
C.正比例函数和一次函数的图象都是直线
D.正比例函数的图象是一条过原点的直线
【考点】一次函数的定义;正比例函数的定义.
【分析】分别利用一次函数和反比例函数的定义以及其性质分析得出即可.
【解答】解:A、所有的正比例函数肯定是一次函数,正确,不合题意;
B、一次函数的一般形式是y=kx+b(k≠0),故此选项错误,符合题意;
C、正比例函数和一次函数的图象都是直线,正确,不合题意;
D、正比例函数的图象是一条过原点的直线,正确,不合题意;
故选:B.
【点评】此题主要考查了一次函数和反比例函数的定义,正确把握其性质是解题关键.
13.直线y=ax+b(a<0,b>0)不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】一次函数图象与系数的关系.
【专题】存在型.
【分析】先根据一次函数的图象与系数的关系得出直线y=ax+b(a<0,b>0)所经过的象限,故可得出结论.
【解答】解:∵直线y=ax+b中,a<0,b>0,
∴直线y=ax+b经过一、二、四象限,
∴不经过第三象限.
故选C.
【点评】本题考查的是一次函数的图象与系数的关系,即一次函数y=kx+b(k≠0)中,当k<0,b>0时函数的图象经过一、二、四象限.
三、解答题(共48分)
14.已知一个正比例函数和一个一次函数的图象相交于点A(1,4),且一次函数的图象与x轴交于点B(3,0)
(1)求这两个函数的解析式;
(2)画出它们的图象.
【考点】两条直线相交或平行问题.
【专题】计算题.
【分析】(1)利用待定系数法求两个函数解析式;
(2)利用描点法画出两函数图象.
【解答】解:(1)设正比例函数解析式为y=kx,
把A(1,4)代入得k=4,
所以正比例函数解析式为y=4x;
设一次函数解析式为y=ax+b,
把A(1,4),B(3,0)代入得,
解得,
所以一次函数解析式为y=﹣2x+6;
(2)如图:
( http: / / www.21cnjy.com )
【点评】本题考查了两条直线相交或平行问题: ( http: / / www.21cnjy.com )若直线y=k1x+b1与直线y=k2x+b2平行,则k1=k2;若直线y=k1x+b1与直线y=k2x+b2相交,则由两解析式所组成的方程组的解为交点坐标.也考查了待定系数法求函数解析式.
15.已知y﹣2与x成正比,且当x=1时,y=﹣6
(1)求y与x之间的函数关系式;
(2)若点(a,2)在这个函数图象上,求a.
【考点】待定系数法求一次函数解析式;一次函数图象上点的坐标特征.
【分析】(1)首先设 y﹣2=kx,再把x=1,y=6代入所设的关系式,即可算出k的值,进而得到y与x之间的函数关系式;
(2)把(a,2)代入(1)中所求的关系式即可得到a的值.
【解答】解:(1)设 y﹣2=kx
∵当x=1时,y=﹣6,
∴k=﹣6﹣2,
∴k=﹣8,
∴y与x之间的函数关系式为y﹣2=﹣8x,即y=﹣8x+2.
(2)∵点(a,2)在这个函数图象上,
∴﹣8a+2=2,
∴a=0.
【点评】此题主要考查了待定系数法求一次函数关系式,关键是掌握凡是图象经过的点必能满足解析式.
16.已知一次函数y=kx+b的图象经过点(﹣1,﹣5),且与正比例函数y=x的图象相交于点(2,a),求:
(1)a的值;
(2)k,b的值;
(3)这两个函数图象与x轴所围成的三角形的面积.
【考点】两条直线相交或平行问题.
【专题】计算题;待定系数法.
【分析】(1)由题知,点(2,a)在正比例函数图象上,代入即可求得a的值.
(2)把点(﹣1,﹣5)及点(2,a)代入一次函数解析式,再根据(1)即可求得k,b的值.
(3)由于正比例函数过原点,又有两个函数交点,求面积只需知道一次函数与x轴的交点即可,S=×a×x.
【解答】解:(1)由题知,把(2,a)代入y=x,
解得a=1;
(2)由题意知,把点(﹣1,﹣5)及点(2,a)代入一次函数解析式得:﹣k+b=﹣5,2k+b=a,
又由(1)知a=1,
解方程组得到:k=2,b=﹣3;
(3)由(2)知一次函数解析式为:y=2x﹣3,
y=2x﹣3与x轴交点坐标为(,0)
∴所求三角形面积S=×1×=;
【点评】本题考查了一次函数图象上点的坐标的性质以及正比例函数图象上点的坐标的性质,是基础题型.
17.某市自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费1.8元,超计划部分每吨按2.0元收费.
(1)写出该单位水费y(元)与每月用水量x(吨)之间的函数关系式:
①当用水量小于等于3000吨时:y=1.8x;②当用水量大于3000吨时:y=2x﹣600.
(2)某月该单位用水3200吨,水费是5800 元;若用水2800吨,水费3240 元.
(3)若某月该单位缴纳水费9400元,则该单位用水多少吨?
【考点】一次函数的应用.
【分析】(1)是个分段函数分①当用水量小于等于3000吨时和②当用水量大于3000吨时.
(2)根据给的用水量,然后代入函数值求解.
(3)代入y=9400,从而可求出x的值.
【解答】解:(1)单位水费y(元)和每月用水量x(吨),
当x≤3000吨时;y=1.8x.
当x>3000吨时:y=3000×1.8+2.0(x﹣3000)=2x﹣600.
(2)单位用水3200吨,水费是:y=2×3200﹣600=5800(元).
若用水2800吨,水费:y=1.8×2800=3240(元).
(3)当该单位缴纳水费9400元,则
9400=2x﹣600,
x=5000.
故此时用水5000吨.
【点评】本题考查一次函数的应用,关键是知道是分段函数,且用水量和钱数之间的关系,从而求解.
18.如图,在直角坐标系中,直线y=kx+4与x轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,求这条直线的解析式.
( http: / / www.21cnjy.com )
【考点】待定系数法求一次函数解析式.
【专题】计算题.
【分析】先根据坐标轴上点的坐标特征得到A(﹣,0),B(0,4),再根据三角形面积公式得到 (﹣) 4=10,然后解方程求出k的值即可得到直线解析式.
【解答】解:当y=0时,kx+4=0,解得x=﹣,则A(﹣,0),
当x=0时,y=kx+4=4,则B(0,4),
因为△OAB的面积为10,
所以 (﹣) 4=10,解得k=﹣,
所以直线解析式为y=﹣x+4.
【点评】本题考查了待定系数法求一次函数解析 ( http: / / www.21cnjy.com )式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.
