山东省德州市三校联考2024-2025学年八年级上学期第一次月考数学试题(PDF版,无答案)
文档属性
| 名称 | 山东省德州市三校联考2024-2025学年八年级上学期第一次月考数学试题(PDF版,无答案) | 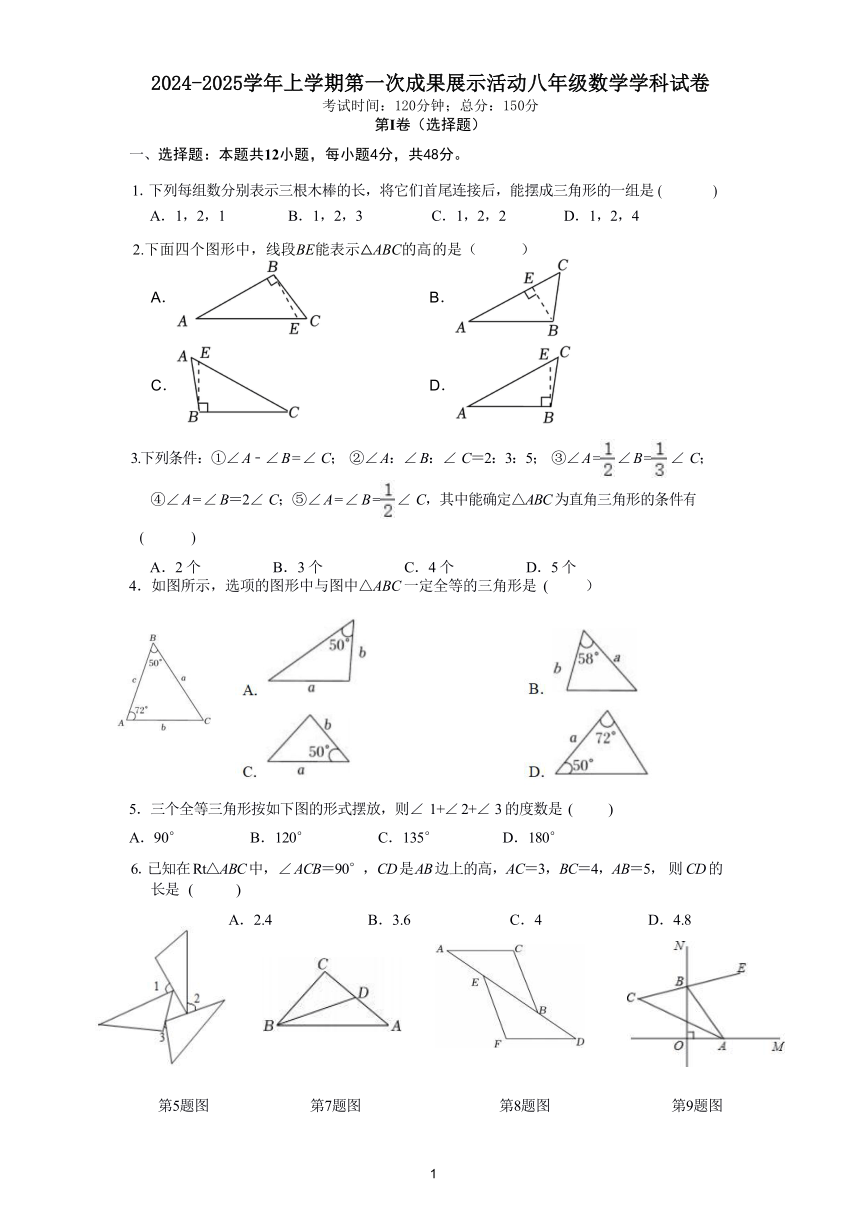 | |
| 格式 | |||
| 文件大小 | 309.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-11 15:44:29 | ||
图片预览


文档简介
2024-2025学年上学期第一次成果展示活动八年级数学学科试卷
考试时间:120分钟;总分:150分
第I卷(选择题)
一、选择题:本题共12小题,每小题4分,共48分。
1.下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是 ( )
A.1,2,1 B.1,2,3 C.1,2,2 D.1,2,4
2.下面四个图形中,线段BE能表示△ABC的高的是( )
A. B.
C. D.
3.下列条件:①∠A﹣∠B=∠ C; ②∠A:∠B:∠ C=2:3:5; ③∠A= ∠B= ∠ C;
④∠A=∠B=2∠ C;⑤∠A=∠B= ∠ C,其中能确定△ABC为直角三角形的条件有
( )
A.2个 B.3个 C.4个 D.5个
4.如图所示,选项的图形中与图中△ABC一定全等的三角形是 ( )
5.三个全等三角形按如下图的形式摆放,则∠ 1+∠ 2+∠ 3的度数是 ( )
A.90° B.120° C.135° D.180°
6.已知在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=3,BC=4,AB=5,则CD的
长是 ( )
A.2.4 B.3.6 C.4 D.4.8
第5题图 第7题图 第8题图 第9题图
1
{#{QQABQQSAgggoAJBAAQhCAwWKCgAQkAAACSgGxFAIIAAAiRNABCA=}#}
7.如图,在△ABC中,AB=15,BC=9,BD是AC边上的中线,若△ABD的周长为 30,则
△BCD的周长是 ( )
A.20 B.24 C.26 D.2
8.如图,在△ABC和△DEF中,点A,E,B,D在同一直线上,AC∥ DF,AC=DF,只添加
一个条件,能判定△ABC≌ △DEF的是 ( )
A.BC=DE B.AE=DB C. ∠A=∠DEF D. ∠ABC=∠D
9.如图,∠MON=90。,点A,B分别在射线OM,ON上运动,BE平分∠NBA,BE的反向延
长线与∠BAO的平分线交于点C,则∠ C的度数是 ( )
A.30° B.45° C.55° D.60°
10.如图,有一个三角形纸片ABC,∠A=65。,∠B=75。,将纸片的一角折叠,使点C落在
△ABC外,若∠2=35。,则∠ 1的度数为 ( )
A.95° B.105° C.115° D.125°
第10题图 第11题图 第12题图
11.两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中 AD=CD,
AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:
①AC丄BD;②AO=CO= AC;③△ABD≌ △CBD;④四边形ABCD的面积= AC×BD
其中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
12.如图,已知线段AB=20米,MA丄AB于点A,MA=6米,射线BD丄AB于B,P点从B点向
A运动,每秒走 1米,Q点从B点向D运动,每秒走 3米,P、Q 同时从B出发,则出发x
秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为 ( )
A.5 B.5或 10 C.10 D.6或 10
第II卷(非选择题)
二、填空题:本题共6小题,每小题4分,共24分。
13.人站在晃动的公共汽车上.若你分开两腿站立,则需伸出一只手去抓栏杆才能站稳,这是利
用了 .
14.已知等腰三角形的三边长为 a,b,c,满足 a - 3 b 7 0,那么三角形周长是
15.如下图,点D,E,F分别是边BC,AD,AC上的中点,若图中阴影部分的面积为 3,则
△ABC的面积是 .
2
{#{QQABQQSAgggoAJBAAQhCAwWKCgAQkAAACSgGxFAIIAAAiRNABCA=}#}
16.如下图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多
边形,则原多边形的边数为 .
17.如下图所示,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE是 度.
18.如图,在△ABC中,∠A=α, ∠ABC和∠ ACD的平分线交于点 A1,得∠ A1;∠ A1BC
和∠ A1CD 的平分线交于点 A2 ,得∠ A2;...∠ A2020BC 和∠ A2020CD 的平分线交于点
A2021,则∠ A2021 = .
三、解答题:本题共7小题,共78分。解答应写出文字说明,证明过程或演算步骤。
19.(10分)已知三角形的两边长为4和 6,第三条边长x最小.
(1)求x的取值范围;
(2)当x为何值时,组成三角形周长最大?最大值是多少?
20.(10分)已知某正多边形的一个内角都比与它相邻外角的3倍还多20。.
(1)求这个正多边形一个内角的度数;
(2)求这个正多边形的内角和.
21.(10分)如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,
∠BAC= 60°,∠ C=50°,求∠DAE及∠BOA的度数.
22.(10分)如图,四边形ABCD中,E点在AD上,∠BAE=∠BCE=90°,且BC=CE,AB
=DE.
(1)求证:△ABC≌ △DEC
(2)求∠DCA的度数.
3
{#{QQABQQSAgggoAJBAAQhCAwWKCgAQkAAACSgGxFAIIAAAiRNABCA=}#}
23.(12分)如图,在△ABC中,点E是AB延长线上一点,且BE=AB.
(1)尺规作图:在∠ CBE内作射线BD,使BD∥ AC.(保留作图痕迹,不要求写作法)
(2)在BD上取点F,使BF=AC,连接EF,求证△ABC≌ △BEF.
23.(12分)如图,在△ABC中,AB=AC,AD丄BC于点D,E为AC边上一点,连接BE与
AD交于点F,G为△ABC外一点,满足∠ ACG=∠ ABE,∠ FAG=∠ BAC,连接EG.
(1)求证:△ABF≌ △ACG;
(2)求证:BE=CG+EG.
25.(14分)在△ABC中,∠BAC=90°,AC=AB,直线MN经过点A,且CD丄MN于D,BE丄
MN于E.
(1)当直线MN绕点A旋转到图 1的位置时,∠ EAB+∠DAC= 度;
(2)在(1)条件下,求证:DE=CD+BE;
(3)当直线MN绕点A旋转到图 2的位置时,试问DE、CD、BE具有怎样的等量关系?请
写出这个等量关系,并加以证明.
4
{#{QQABQQSAgggoAJBAAQhCAwWKCgAQkAAACSgGxFAIIAAAiRNABCA=}#}
考试时间:120分钟;总分:150分
第I卷(选择题)
一、选择题:本题共12小题,每小题4分,共48分。
1.下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是 ( )
A.1,2,1 B.1,2,3 C.1,2,2 D.1,2,4
2.下面四个图形中,线段BE能表示△ABC的高的是( )
A. B.
C. D.
3.下列条件:①∠A﹣∠B=∠ C; ②∠A:∠B:∠ C=2:3:5; ③∠A= ∠B= ∠ C;
④∠A=∠B=2∠ C;⑤∠A=∠B= ∠ C,其中能确定△ABC为直角三角形的条件有
( )
A.2个 B.3个 C.4个 D.5个
4.如图所示,选项的图形中与图中△ABC一定全等的三角形是 ( )
5.三个全等三角形按如下图的形式摆放,则∠ 1+∠ 2+∠ 3的度数是 ( )
A.90° B.120° C.135° D.180°
6.已知在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=3,BC=4,AB=5,则CD的
长是 ( )
A.2.4 B.3.6 C.4 D.4.8
第5题图 第7题图 第8题图 第9题图
1
{#{QQABQQSAgggoAJBAAQhCAwWKCgAQkAAACSgGxFAIIAAAiRNABCA=}#}
7.如图,在△ABC中,AB=15,BC=9,BD是AC边上的中线,若△ABD的周长为 30,则
△BCD的周长是 ( )
A.20 B.24 C.26 D.2
8.如图,在△ABC和△DEF中,点A,E,B,D在同一直线上,AC∥ DF,AC=DF,只添加
一个条件,能判定△ABC≌ △DEF的是 ( )
A.BC=DE B.AE=DB C. ∠A=∠DEF D. ∠ABC=∠D
9.如图,∠MON=90。,点A,B分别在射线OM,ON上运动,BE平分∠NBA,BE的反向延
长线与∠BAO的平分线交于点C,则∠ C的度数是 ( )
A.30° B.45° C.55° D.60°
10.如图,有一个三角形纸片ABC,∠A=65。,∠B=75。,将纸片的一角折叠,使点C落在
△ABC外,若∠2=35。,则∠ 1的度数为 ( )
A.95° B.105° C.115° D.125°
第10题图 第11题图 第12题图
11.两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中 AD=CD,
AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:
①AC丄BD;②AO=CO= AC;③△ABD≌ △CBD;④四边形ABCD的面积= AC×BD
其中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
12.如图,已知线段AB=20米,MA丄AB于点A,MA=6米,射线BD丄AB于B,P点从B点向
A运动,每秒走 1米,Q点从B点向D运动,每秒走 3米,P、Q 同时从B出发,则出发x
秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为 ( )
A.5 B.5或 10 C.10 D.6或 10
第II卷(非选择题)
二、填空题:本题共6小题,每小题4分,共24分。
13.人站在晃动的公共汽车上.若你分开两腿站立,则需伸出一只手去抓栏杆才能站稳,这是利
用了 .
14.已知等腰三角形的三边长为 a,b,c,满足 a - 3 b 7 0,那么三角形周长是
15.如下图,点D,E,F分别是边BC,AD,AC上的中点,若图中阴影部分的面积为 3,则
△ABC的面积是 .
2
{#{QQABQQSAgggoAJBAAQhCAwWKCgAQkAAACSgGxFAIIAAAiRNABCA=}#}
16.如下图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多
边形,则原多边形的边数为 .
17.如下图所示,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE是 度.
18.如图,在△ABC中,∠A=α, ∠ABC和∠ ACD的平分线交于点 A1,得∠ A1;∠ A1BC
和∠ A1CD 的平分线交于点 A2 ,得∠ A2;...∠ A2020BC 和∠ A2020CD 的平分线交于点
A2021,则∠ A2021 = .
三、解答题:本题共7小题,共78分。解答应写出文字说明,证明过程或演算步骤。
19.(10分)已知三角形的两边长为4和 6,第三条边长x最小.
(1)求x的取值范围;
(2)当x为何值时,组成三角形周长最大?最大值是多少?
20.(10分)已知某正多边形的一个内角都比与它相邻外角的3倍还多20。.
(1)求这个正多边形一个内角的度数;
(2)求这个正多边形的内角和.
21.(10分)如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,
∠BAC= 60°,∠ C=50°,求∠DAE及∠BOA的度数.
22.(10分)如图,四边形ABCD中,E点在AD上,∠BAE=∠BCE=90°,且BC=CE,AB
=DE.
(1)求证:△ABC≌ △DEC
(2)求∠DCA的度数.
3
{#{QQABQQSAgggoAJBAAQhCAwWKCgAQkAAACSgGxFAIIAAAiRNABCA=}#}
23.(12分)如图,在△ABC中,点E是AB延长线上一点,且BE=AB.
(1)尺规作图:在∠ CBE内作射线BD,使BD∥ AC.(保留作图痕迹,不要求写作法)
(2)在BD上取点F,使BF=AC,连接EF,求证△ABC≌ △BEF.
23.(12分)如图,在△ABC中,AB=AC,AD丄BC于点D,E为AC边上一点,连接BE与
AD交于点F,G为△ABC外一点,满足∠ ACG=∠ ABE,∠ FAG=∠ BAC,连接EG.
(1)求证:△ABF≌ △ACG;
(2)求证:BE=CG+EG.
25.(14分)在△ABC中,∠BAC=90°,AC=AB,直线MN经过点A,且CD丄MN于D,BE丄
MN于E.
(1)当直线MN绕点A旋转到图 1的位置时,∠ EAB+∠DAC= 度;
(2)在(1)条件下,求证:DE=CD+BE;
(3)当直线MN绕点A旋转到图 2的位置时,试问DE、CD、BE具有怎样的等量关系?请
写出这个等量关系,并加以证明.
4
{#{QQABQQSAgggoAJBAAQhCAwWKCgAQkAAACSgGxFAIIAAAiRNABCA=}#}
同课章节目录
