山东省济南天桥区泺口实验学校2024-2025学年八年级上学期数学第一次月考试卷(含答案)
文档属性
| 名称 | 山东省济南天桥区泺口实验学校2024-2025学年八年级上学期数学第一次月考试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 458.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-11 16:32:00 | ||
图片预览



文档简介
泺口实验学校2024—2025学年度第一学期八年级数学质量检测试题
本试题分第I卷(选择题)和第II卷(非选择题)两部分,共4页.满分150分,考试时间120分钟.
第I卷(选择题 共40分).
一.选择题.(共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一个最符合题目要求。)
1.下列各数中是无理数的是( )
A.3.1415 B. C. D.
2.在平面直角坐标系中,点(3,-4)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列说法中正确的是( )
A.=±4 B.0.09的平方根是0.3 C.1的立方根是±1 D.0的立方根是0
4.根据下列表述,能确定准确位置的是( )
A.万达影城3号厅2排 B.经十路中段 C.南偏东40° D.东经117°,北纬36°
5.下列运算正确的是( )
A.+= B.2×= C.3﹣=3 D.÷=2
6.已知点P在第四象限,且点P到x轴的距离为3,到y轴的距离为4,则点P坐标为( )
A.(3,﹣4) B.(-3,4) C.(-4,3) D.(3,-4)
7.如图,湖的两岸有A,C两点,在与AC成直角的BC方向上的点C处测得AB=15米,BC=12米,则A,C两点间的距离为( )
A.3米 B.6米 C.9米 D.10米
8.已知P点坐标为(3,2a+2),且点P在x轴上,则a的值是( )
A.0 B.-1 C.-2 D.-3
9.已知直线MN∥x轴,M点的坐标为(2,3),并且线段MN=3,则点N的坐标为( )
A.(-1,3) B.(5,3) C.(1,3)或(5,3) D.(-1,3)或(5,3)
10.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)…,那么点A2022的坐标为( )
A.(1011,0) B.(1011,1) C.(2022,0) D.(2022,1)
第II卷(非选择题 共110分)
二.填空题:(每题4分,共20分)
11.如果用有序数对(1,4)表示第一单元4号的住户,那么第二单元8号的住户用有序数
对表示为 。
12.比较大小: 4.
13.在平面直角坐标系内,点(-3,1)关于y轴对称的点的坐标为 。
14.如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴于一点,则这个点表示的实数是 。
(第14题图) (第15题图)
15.实数a、b在数轴上对应点的位置如图,则+的结果是 。
三.解答题:
16.(7分)计算:(1) (2)-+
17.(7分)计算:(1)﹣2 (2)(﹣)2
18.(7分)解方程:(1)(x-4)2-9=0; (2)(x+1)3=-27.
19.(8分)把下列各数的序号填在相应的横线里:
①-3,②0,③,④-,⑤,⑥,⑦0.3,⑧0.101001000…(每两个1之间依次多一个0
整数集合:{ …} 分数集合:{ …}
无理数集合:{ …} 非负有理数集合:{ …}
20.(8分)已知3a+2的立方根是2,3a+b-1的算术平方根是4,c是的整数部分.
(1)求a、b、c的值;
(2)求a+b-c的平方根.
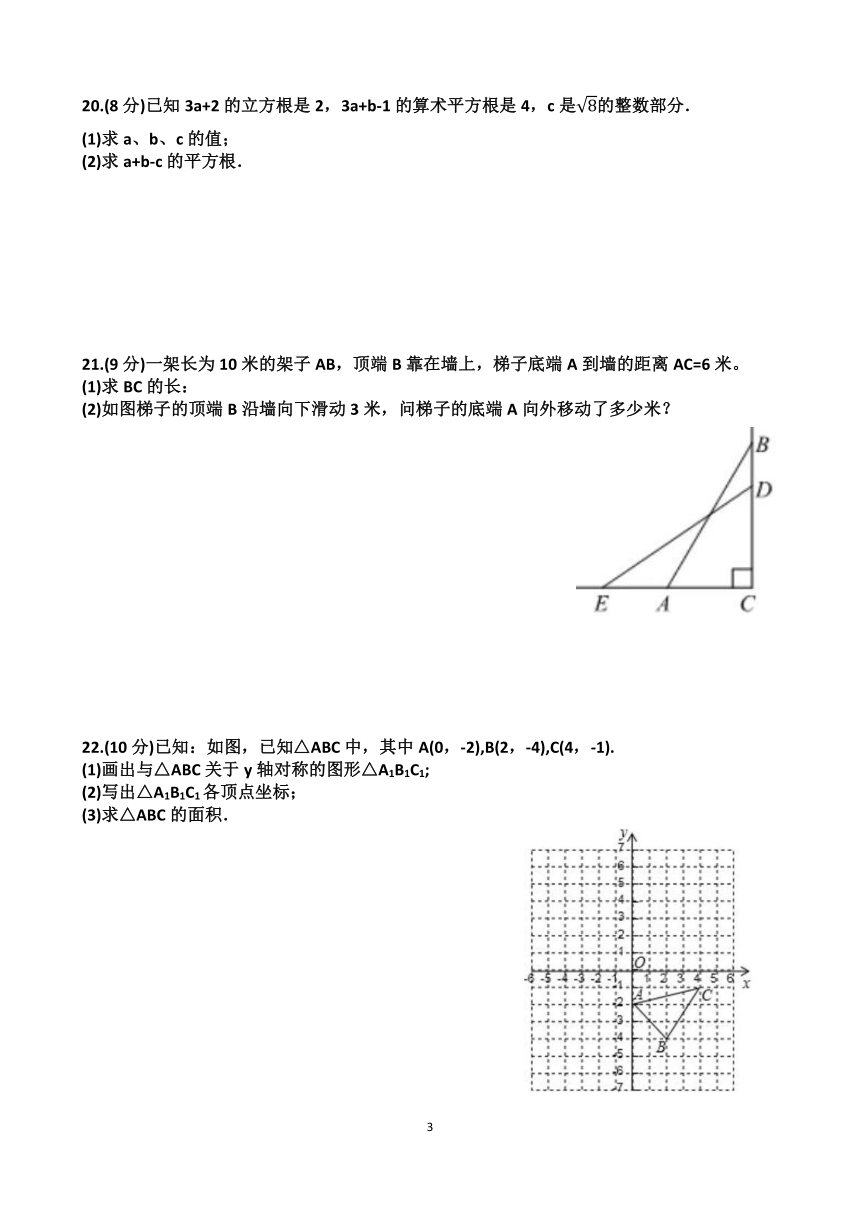
21.(9分)一架长为10米的架子AB,顶端B靠在墙上,梯子底端A到墙的距离AC=6米。
(1)求BC的长:
(2)如图梯子的顶端B沿墙向下滑动3米,问梯子的底端A向外移动了多少米?
22.(10分)已知:如图,已知△ABC中,其中A(0,-2),B(2,-4),C(4,-1).
(1)画出与△ABC关于y轴对称的图形△A1B1C1;
(2)写出△A1B1C1各顶点坐标;
(3)求△ABC的面积.
23.(10分)在如图所示的正方形网格中,每个小正方形的边长为1,格点△ABC(顶点是网格线的交点的三角形)的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A'B'C';
(3)在y轴上存在一点P,满足点P到点A与点B距离之和最小,请直接写出PA+PB的最小值为 .
24.(12分)阅读下面计算过程:
==
==
==
请解决下列问题:
(1)观察上式并填空:= 。
(2)观察上述规律并猜想:当n是正整数时,= 。
(3)请利用(2)的结论并计算:(++...++)×(1)
25.(12分)
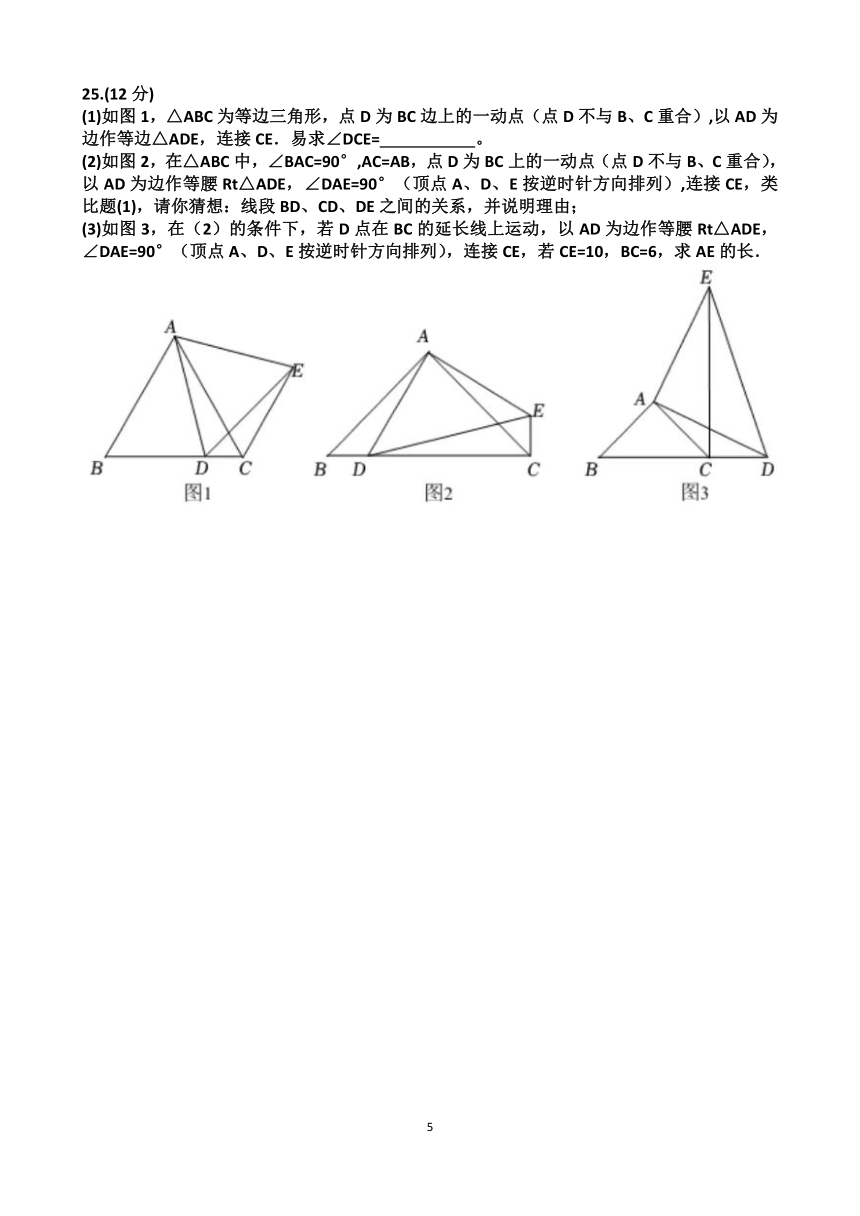
(1)如图1,△ABC为等边三角形,点D为BC边上的一动点(点D不与B、C重合),以AD为边作等边△ADE,连接CE.易求∠DCE= 。
(2)如图2,在△ABC中,∠BAC=90°,AC=AB,点D为BC上的一动点(点D不与B、C重合),以AD为边作等腰Rt△ADE,∠DAE=90°(顶点A、D、E按逆时针方向排列),连接CE,类比题(1),请你猜想:线段BD、CD、DE之间的关系,并说明理由;
(3)如图3,在(2)的条件下,若D点在BC的延长线上运动,以AD为边作等腰Rt△ADE,∠DAE=90°(顶点A、D、E按逆时针方向排列),连接CE,若CE=10,BC=6,求AE的长.
答案
一.选择题.(共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一个最符合题目要求。)
1.下列各数中是无理数的是( B )
A.3.1415 B. C. D.
2.在平面直角坐标系中,点(3,-4)所在的象限是( D )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列说法中正确的是( D )
A.=±4 B.0.09的平方根是0.3 C.1的立方根是±1 D.0的立方根是0
4.根据下列表述,能确定准确位置的是( D )
A.万达影城3号厅2排 B.经十路中段 C.南偏东40° D.东经117°,北纬36°
5.下列运算正确的是( D )
A.+= B.2×= C.3﹣=3 D.÷=2
6.已知点P在第四象限,且点P到x轴的距离为3,到y轴的距离为4,则点P坐标为( D )
A.(3,﹣4) B.(-3,4) C.(-4,3) D.(3,-4)
7.如图,湖的两岸有A,C两点,在与AC成直角的BC方向上的点C处测得AB=15米,BC=12米,则A,C两点间的距离为( C )
A.3米 B.6米 C.9米 D.10米
8.已知P点坐标为(3,2a+2),且点P在x轴上,则a的值是( B )
A.0 B.-1 C.-2 D.-3
9.已知直线MN∥x轴,M点的坐标为(2,3),并且线段MN=3,则点N的坐标为( D )
A.(-1,3) B.(5,3) C.(1,3)或(5,3) D.(-1,3)或(5,3)
10.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)…,那么点A2022的坐标为( B )
A.(1011,0) B.(1011,1) C.(2022,0) D.(2022,1)
第II卷(非选择题 共110分)
二.填空题:(每题4分,共20分)
11.如果用有序数对(1,4)表示第一单元4号的住户,那么第二单元8号的住户用有序数
对表示为 (2,8) 。
12.比较大小: > 4.
13.在平面直角坐标系内,点(-3,1)关于y轴对称的点的坐标为 (3,1) 。
14.如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴于一点,则这个点表示的实数是 。
(第14题图) (第15题图)
15.实数a、b在数轴上对应点的位置如图,则+的结果是 b﹣2a 。
三.解答题:
16.(7分)计算:(1) (2)-+
=× =3﹣2+
=3 =
17.(7分)计算:(1)﹣2 (2)(﹣)2
=2+1﹣2 =5﹣2+2
=1 =7﹣2
18.(7分)解方程:(1)(x-4)2-9=0; (2)(x+1)3=-27.
x﹣4=±3 x+1=﹣3
x=7或x=1 x=﹣4
19.(8分)把下列各数的序号填在相应的横线里:
①-3,②0,③,④-,⑤,⑥,⑦0.3,⑧0.101001000…(每两个1之间依次多一个0
整数集合:{ ①②④ …} 分数集合:{ ⑥⑦ …}
无理数集合:{ ③⑤⑧ …} 非负有理数集合:{ ②⑥⑦ …}
20.(8分)已知3a+2的立方根是2,3a+b-1的算术平方根是4,c是的整数部分.
(1)求a、b、c的值;
(2)求a+b-c的平方根.
(1)∵3a+2的立方根是2,3a+b-1的算术平方根是4
∴3a+2=8,3a+b-1=16
解得:a=2,b=11
∵4<8<9,
∴2<<3
∴的整数部分是2
∴c=2
∴a=2,b=11,c=2
∵a=2,b=11,c=2
∴a+b-c=2+11-2=11
∴a+b-c的平方根是±
21.(9分)一架长为10米的架子AB,顶端B靠在墙上,梯子底端A到墙的距离AC=6米。
(1)求BC的长:
(2)如图梯子的顶端B沿墙向下滑动3米,问梯子的底端A向外移动了多少米?
(1)∵一架长10米的梯子AB,顶端B靠在墙上,梯子底端A到墙的距离AC=6米
∴BC==8(米)
答:BC的长为8米.
(2)∵BD=3,BC=8
∴CD=BC﹣BD=8-3=5
∴CE==5
∴AE=CE﹣AC=(5-6)(米)。
答:梯子的底端A向外移动了(5-6)米.
22.(10分)已知:如图,已知△ABC中,其中A(0,-2),B(2,-4),C(4,-1).
(1)画出与△ABC关于y轴对称的图形△A1B1C1;
(2)写出△A1B1C1各顶点坐标;
(3)求△ABC的面积.
(1)略
(2)A1(0,﹣2) B1(﹣2,﹣4) C1(﹣4,﹣1)
(3)3×4﹣×1×4﹣×2×2﹣×2×3=5
23.(10分)在如图所示的正方形网格中,每个小正方形的边长为1,格点△ABC(顶点是网格线的交点的三角形)的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A'B'C';
(3)在y轴上存在一点P,满足点P到点A与点B距离之和最小,请直接写出PA+PB的最小值为 .
(1)
(2)
(3)2
24.(12分)阅读下面计算过程:
==
==
==
请解决下列问题:
(1)观察上式并填空:= 。
(2)观察上述规律并猜想:当n是正整数时,= 。
(3)请利用(2)的结论并计算:
(++...++)×(1)
(1)
(2)
(3)(++...++)×(1)
=(1)(1)
=2020﹣1
=2019
25.(12分)
(1)如图1,△ABC为等边三角形,点D为BC边上的一动点(点D不与B、C重合),以AD为边作等边△ADE,连接CE.易求∠DCE= 。
(2)如图2,在△ABC中,∠BAC=90°,AC=AB,点D为BC上的一动点(点D不与B、C重合),以AD为边作等腰Rt△ADE,∠DAE=90°(顶点A、D、E按逆时针方向排列),连接CE,类比题(1),请你猜想:线段BD、CD、DE之间的关系,并说明理由;
(3)如图3,在(2)的条件下,若D点在BC的延长线上运动,以AD为边作等腰Rt△ADE,∠DAE=90°(顶点A、D、E按逆时针方向排列),连接CE,若CE=10,BC=6,求AE的长.
∵△ABC和△ADE都是等边三角形
∴AB=AC,AD=AE,∠B=∠ACB=∠BAC=∠DAE=60°
∴∠BAD+∠CAD=∠DAE﹣∠CAD
∴∠BAD=∠CAE
∴△ABD≌△ACE(SAS)
∴∠B=∠ACE=60°
∴∠DCE=∠ACB+∠ACE=120°
故答案为:120°
(2)DE2=CD2+BD2;理由如下:
在Rt△ABC,AB=AC
∴∠B=∠ACB=45°
∵∠BAC=∠DAE=90°
∴∠BAD=∠CAE
∵AD=AE
∴△ABD≌△ACE(SAS)
∴BD=CE,∠ACE=∠B=45°
∴∠BCE=∠ACB+∠ACE=90°
根据勾股定理得,
DE2=CD2+CE2=CD2+BD2
(3)由(2)知,BD=CE
∵CE=10
∴BD=10
∵BC=6
∴CD=BD﹣BC=4
由(2)知,∠BCE=90°
∴∠DCE =90°
根据勾股定理得,DE2=CE2+CD2=116
在Rt△ADE中,DE2=2AE2=116
∴AE=
本试题分第I卷(选择题)和第II卷(非选择题)两部分,共4页.满分150分,考试时间120分钟.
第I卷(选择题 共40分).
一.选择题.(共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一个最符合题目要求。)
1.下列各数中是无理数的是( )
A.3.1415 B. C. D.
2.在平面直角坐标系中,点(3,-4)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列说法中正确的是( )
A.=±4 B.0.09的平方根是0.3 C.1的立方根是±1 D.0的立方根是0
4.根据下列表述,能确定准确位置的是( )
A.万达影城3号厅2排 B.经十路中段 C.南偏东40° D.东经117°,北纬36°
5.下列运算正确的是( )
A.+= B.2×= C.3﹣=3 D.÷=2
6.已知点P在第四象限,且点P到x轴的距离为3,到y轴的距离为4,则点P坐标为( )
A.(3,﹣4) B.(-3,4) C.(-4,3) D.(3,-4)
7.如图,湖的两岸有A,C两点,在与AC成直角的BC方向上的点C处测得AB=15米,BC=12米,则A,C两点间的距离为( )
A.3米 B.6米 C.9米 D.10米
8.已知P点坐标为(3,2a+2),且点P在x轴上,则a的值是( )
A.0 B.-1 C.-2 D.-3
9.已知直线MN∥x轴,M点的坐标为(2,3),并且线段MN=3,则点N的坐标为( )
A.(-1,3) B.(5,3) C.(1,3)或(5,3) D.(-1,3)或(5,3)
10.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)…,那么点A2022的坐标为( )
A.(1011,0) B.(1011,1) C.(2022,0) D.(2022,1)
第II卷(非选择题 共110分)
二.填空题:(每题4分,共20分)
11.如果用有序数对(1,4)表示第一单元4号的住户,那么第二单元8号的住户用有序数
对表示为 。
12.比较大小: 4.
13.在平面直角坐标系内,点(-3,1)关于y轴对称的点的坐标为 。
14.如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴于一点,则这个点表示的实数是 。
(第14题图) (第15题图)
15.实数a、b在数轴上对应点的位置如图,则+的结果是 。
三.解答题:
16.(7分)计算:(1) (2)-+
17.(7分)计算:(1)﹣2 (2)(﹣)2
18.(7分)解方程:(1)(x-4)2-9=0; (2)(x+1)3=-27.
19.(8分)把下列各数的序号填在相应的横线里:
①-3,②0,③,④-,⑤,⑥,⑦0.3,⑧0.101001000…(每两个1之间依次多一个0
整数集合:{ …} 分数集合:{ …}
无理数集合:{ …} 非负有理数集合:{ …}
20.(8分)已知3a+2的立方根是2,3a+b-1的算术平方根是4,c是的整数部分.
(1)求a、b、c的值;
(2)求a+b-c的平方根.
21.(9分)一架长为10米的架子AB,顶端B靠在墙上,梯子底端A到墙的距离AC=6米。
(1)求BC的长:
(2)如图梯子的顶端B沿墙向下滑动3米,问梯子的底端A向外移动了多少米?
22.(10分)已知:如图,已知△ABC中,其中A(0,-2),B(2,-4),C(4,-1).
(1)画出与△ABC关于y轴对称的图形△A1B1C1;
(2)写出△A1B1C1各顶点坐标;
(3)求△ABC的面积.
23.(10分)在如图所示的正方形网格中,每个小正方形的边长为1,格点△ABC(顶点是网格线的交点的三角形)的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A'B'C';
(3)在y轴上存在一点P,满足点P到点A与点B距离之和最小,请直接写出PA+PB的最小值为 .
24.(12分)阅读下面计算过程:
==
==
==
请解决下列问题:
(1)观察上式并填空:= 。
(2)观察上述规律并猜想:当n是正整数时,= 。
(3)请利用(2)的结论并计算:(++...++)×(1)
25.(12分)
(1)如图1,△ABC为等边三角形,点D为BC边上的一动点(点D不与B、C重合),以AD为边作等边△ADE,连接CE.易求∠DCE= 。
(2)如图2,在△ABC中,∠BAC=90°,AC=AB,点D为BC上的一动点(点D不与B、C重合),以AD为边作等腰Rt△ADE,∠DAE=90°(顶点A、D、E按逆时针方向排列),连接CE,类比题(1),请你猜想:线段BD、CD、DE之间的关系,并说明理由;
(3)如图3,在(2)的条件下,若D点在BC的延长线上运动,以AD为边作等腰Rt△ADE,∠DAE=90°(顶点A、D、E按逆时针方向排列),连接CE,若CE=10,BC=6,求AE的长.
答案
一.选择题.(共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一个最符合题目要求。)
1.下列各数中是无理数的是( B )
A.3.1415 B. C. D.
2.在平面直角坐标系中,点(3,-4)所在的象限是( D )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列说法中正确的是( D )
A.=±4 B.0.09的平方根是0.3 C.1的立方根是±1 D.0的立方根是0
4.根据下列表述,能确定准确位置的是( D )
A.万达影城3号厅2排 B.经十路中段 C.南偏东40° D.东经117°,北纬36°
5.下列运算正确的是( D )
A.+= B.2×= C.3﹣=3 D.÷=2
6.已知点P在第四象限,且点P到x轴的距离为3,到y轴的距离为4,则点P坐标为( D )
A.(3,﹣4) B.(-3,4) C.(-4,3) D.(3,-4)
7.如图,湖的两岸有A,C两点,在与AC成直角的BC方向上的点C处测得AB=15米,BC=12米,则A,C两点间的距离为( C )
A.3米 B.6米 C.9米 D.10米
8.已知P点坐标为(3,2a+2),且点P在x轴上,则a的值是( B )
A.0 B.-1 C.-2 D.-3
9.已知直线MN∥x轴,M点的坐标为(2,3),并且线段MN=3,则点N的坐标为( D )
A.(-1,3) B.(5,3) C.(1,3)或(5,3) D.(-1,3)或(5,3)
10.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)…,那么点A2022的坐标为( B )
A.(1011,0) B.(1011,1) C.(2022,0) D.(2022,1)
第II卷(非选择题 共110分)
二.填空题:(每题4分,共20分)
11.如果用有序数对(1,4)表示第一单元4号的住户,那么第二单元8号的住户用有序数
对表示为 (2,8) 。
12.比较大小: > 4.
13.在平面直角坐标系内,点(-3,1)关于y轴对称的点的坐标为 (3,1) 。
14.如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴于一点,则这个点表示的实数是 。
(第14题图) (第15题图)
15.实数a、b在数轴上对应点的位置如图,则+的结果是 b﹣2a 。
三.解答题:
16.(7分)计算:(1) (2)-+
=× =3﹣2+
=3 =
17.(7分)计算:(1)﹣2 (2)(﹣)2
=2+1﹣2 =5﹣2+2
=1 =7﹣2
18.(7分)解方程:(1)(x-4)2-9=0; (2)(x+1)3=-27.
x﹣4=±3 x+1=﹣3
x=7或x=1 x=﹣4
19.(8分)把下列各数的序号填在相应的横线里:
①-3,②0,③,④-,⑤,⑥,⑦0.3,⑧0.101001000…(每两个1之间依次多一个0
整数集合:{ ①②④ …} 分数集合:{ ⑥⑦ …}
无理数集合:{ ③⑤⑧ …} 非负有理数集合:{ ②⑥⑦ …}
20.(8分)已知3a+2的立方根是2,3a+b-1的算术平方根是4,c是的整数部分.
(1)求a、b、c的值;
(2)求a+b-c的平方根.
(1)∵3a+2的立方根是2,3a+b-1的算术平方根是4
∴3a+2=8,3a+b-1=16
解得:a=2,b=11
∵4<8<9,
∴2<<3
∴的整数部分是2
∴c=2
∴a=2,b=11,c=2
∵a=2,b=11,c=2
∴a+b-c=2+11-2=11
∴a+b-c的平方根是±
21.(9分)一架长为10米的架子AB,顶端B靠在墙上,梯子底端A到墙的距离AC=6米。
(1)求BC的长:
(2)如图梯子的顶端B沿墙向下滑动3米,问梯子的底端A向外移动了多少米?
(1)∵一架长10米的梯子AB,顶端B靠在墙上,梯子底端A到墙的距离AC=6米
∴BC==8(米)
答:BC的长为8米.
(2)∵BD=3,BC=8
∴CD=BC﹣BD=8-3=5
∴CE==5
∴AE=CE﹣AC=(5-6)(米)。
答:梯子的底端A向外移动了(5-6)米.
22.(10分)已知:如图,已知△ABC中,其中A(0,-2),B(2,-4),C(4,-1).
(1)画出与△ABC关于y轴对称的图形△A1B1C1;
(2)写出△A1B1C1各顶点坐标;
(3)求△ABC的面积.
(1)略
(2)A1(0,﹣2) B1(﹣2,﹣4) C1(﹣4,﹣1)
(3)3×4﹣×1×4﹣×2×2﹣×2×3=5
23.(10分)在如图所示的正方形网格中,每个小正方形的边长为1,格点△ABC(顶点是网格线的交点的三角形)的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A'B'C';
(3)在y轴上存在一点P,满足点P到点A与点B距离之和最小,请直接写出PA+PB的最小值为 .
(1)
(2)
(3)2
24.(12分)阅读下面计算过程:
==
==
==
请解决下列问题:
(1)观察上式并填空:= 。
(2)观察上述规律并猜想:当n是正整数时,= 。
(3)请利用(2)的结论并计算:
(++...++)×(1)
(1)
(2)
(3)(++...++)×(1)
=(1)(1)
=2020﹣1
=2019
25.(12分)
(1)如图1,△ABC为等边三角形,点D为BC边上的一动点(点D不与B、C重合),以AD为边作等边△ADE,连接CE.易求∠DCE= 。
(2)如图2,在△ABC中,∠BAC=90°,AC=AB,点D为BC上的一动点(点D不与B、C重合),以AD为边作等腰Rt△ADE,∠DAE=90°(顶点A、D、E按逆时针方向排列),连接CE,类比题(1),请你猜想:线段BD、CD、DE之间的关系,并说明理由;
(3)如图3,在(2)的条件下,若D点在BC的延长线上运动,以AD为边作等腰Rt△ADE,∠DAE=90°(顶点A、D、E按逆时针方向排列),连接CE,若CE=10,BC=6,求AE的长.
∵△ABC和△ADE都是等边三角形
∴AB=AC,AD=AE,∠B=∠ACB=∠BAC=∠DAE=60°
∴∠BAD+∠CAD=∠DAE﹣∠CAD
∴∠BAD=∠CAE
∴△ABD≌△ACE(SAS)
∴∠B=∠ACE=60°
∴∠DCE=∠ACB+∠ACE=120°
故答案为:120°
(2)DE2=CD2+BD2;理由如下:
在Rt△ABC,AB=AC
∴∠B=∠ACB=45°
∵∠BAC=∠DAE=90°
∴∠BAD=∠CAE
∵AD=AE
∴△ABD≌△ACE(SAS)
∴BD=CE,∠ACE=∠B=45°
∴∠BCE=∠ACB+∠ACE=90°
根据勾股定理得,
DE2=CD2+CE2=CD2+BD2
(3)由(2)知,BD=CE
∵CE=10
∴BD=10
∵BC=6
∴CD=BD﹣BC=4
由(2)知,∠BCE=90°
∴∠DCE =90°
根据勾股定理得,DE2=CE2+CD2=116
在Rt△ADE中,DE2=2AE2=116
∴AE=
同课章节目录
