(16)垂直于弦的直径—九年级数学人教版上册课前导学(含答案)
文档属性
| 名称 | (16)垂直于弦的直径—九年级数学人教版上册课前导学(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 531.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-11 21:46:00 | ||
图片预览


文档简介
(16)垂直于弦的直径—九年级数学人教版上册课前导学
一、知识预习
1.圆是轴对称图形,任何一条直径所在直线都是圆的对称轴.
2.垂直于弦的直径 弦,并且 弦所对的两条弧.
符号语言:
∵①CD是直径,②CD⊥AB
∴③AE= ,④= ,⑤= .
3.平分弦(不是直径)的直径 于弦,并且 弦所对的两条弧.
符号语言:
∵①CD是直径 ②AE=BE且AB不是直径
∴③CD⊥ ,④= ,⑤=
二、自我检测
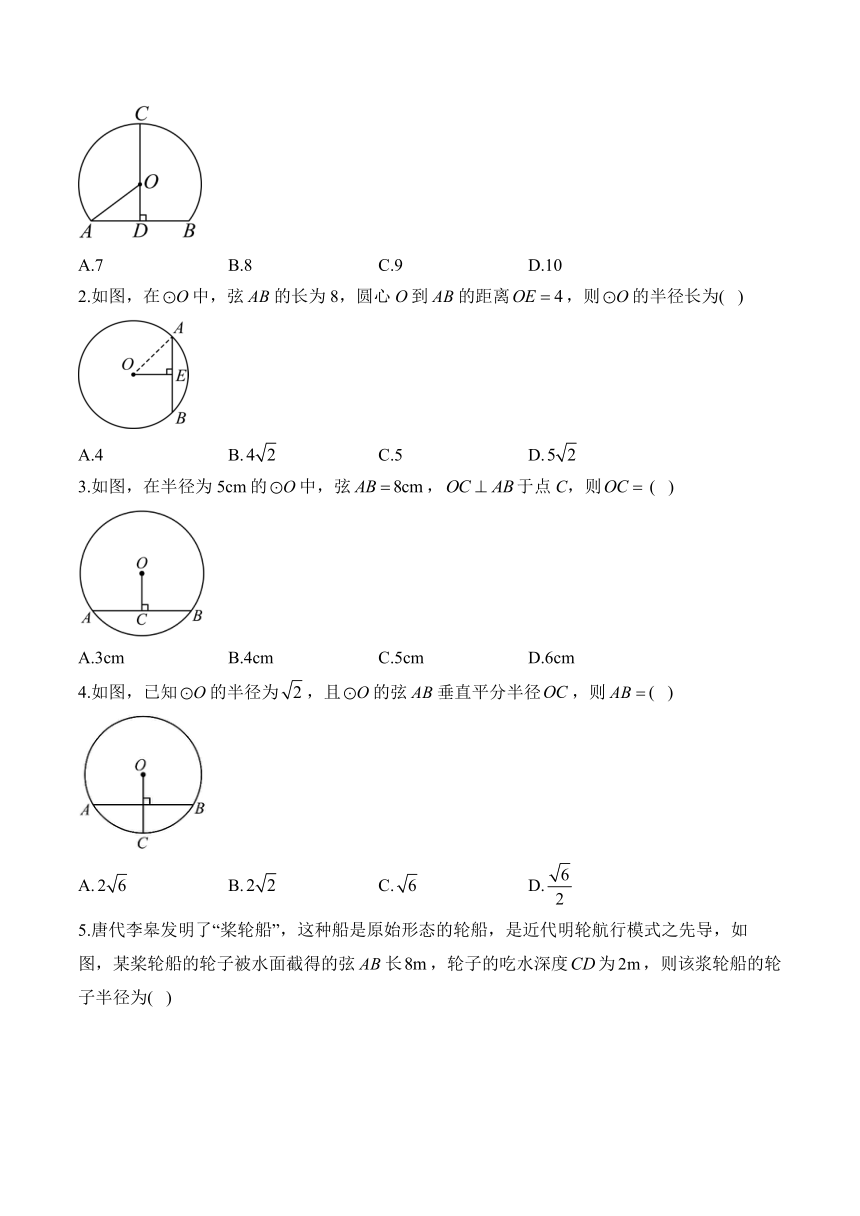
1.如图所示是一个单心圆曲隧道的截面,若隧道单心圆的半径的长是,净高为,则此路面宽为( ).
A.7 B.8 C.9 D.10
2.如图,在中,弦的长为8,圆心O到的距离,则的半径长为( )
A.4 B. C.5 D.
3.如图,在半径为5cm的中,弦,于点C,则 ( )
A.3cm B.4cm C.5cm D.6cm
4.如图,已知的半径为,且的弦垂直平分半径,则( )
A. B. C. D.
5.唐代李皋发明了“桨轮船”,这种船是原始形态的轮船,是近代明轮航行模式之先导,如图,某桨轮船的轮子被水面截得的弦长,轮子的吃水深度为,则该浆轮船的轮子半径为( )
A. B. C. D.
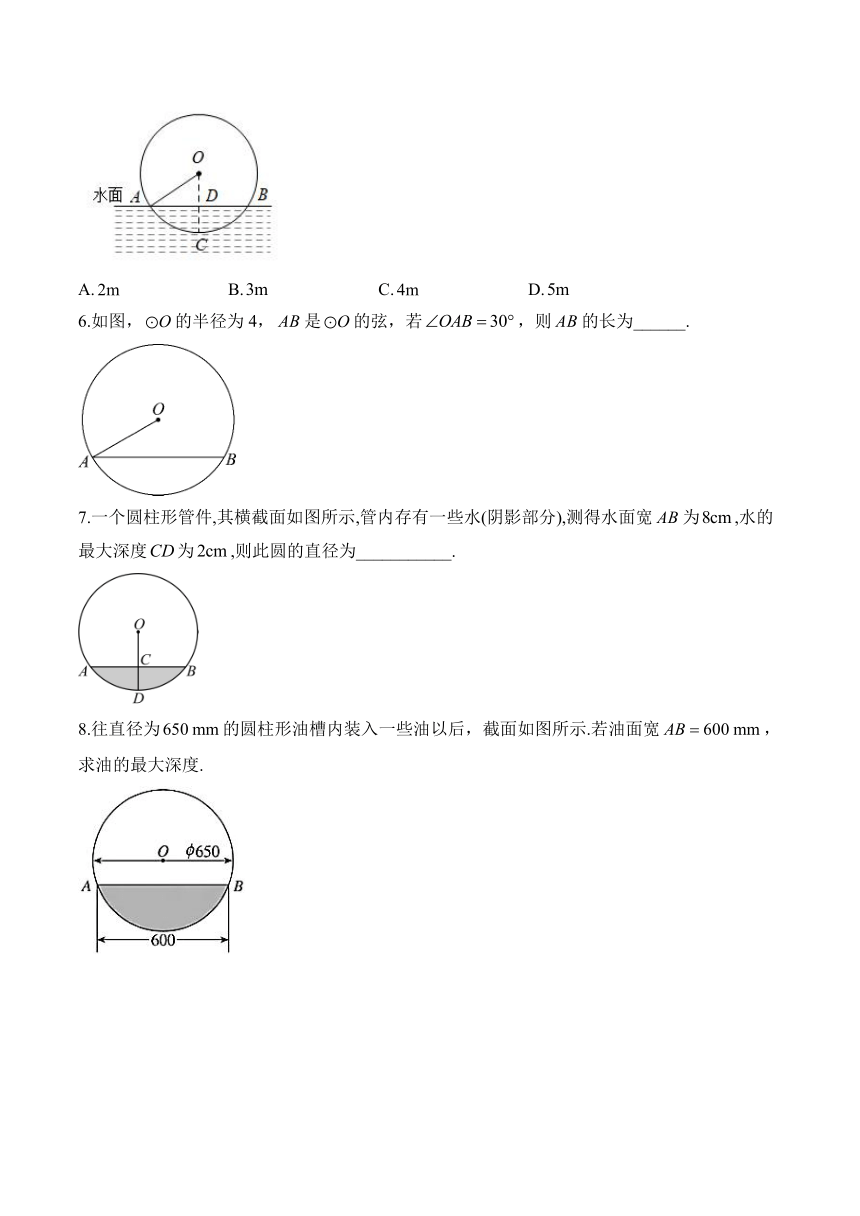
6.如图,的半径为4,是的弦,若,则的长为______.
7.一个圆柱形管件,其横截面如图所示,管内存有一些水(阴影部分),测得水面宽为,水的最大深度为,则此圆的直径为___________.
8.往直径为的圆柱形油槽内装入一些油以后,截面如图所示.若油面宽,求油的最大深度.
答案以及解析
一、知识预习
2. 平分 平分 BE
3. 垂直 平分 AB
二、自我检测
1.答案:B
解析:根据题意得到,
在中,,
,
故选B.
2.答案:B
解析:在中,弦的长为8,圆心O到的距离,
,,
在中,,
故选:B.
3.答案:A
解析:连接,
,
,
,,
在中,,
,.
故选:A.
4.答案:C
解析:如图所示,
∵的半径为,
∴,
∵的弦垂直平分半径,
∴,,
∴,
∴.
故选:C.
5.答案:D
解析:设半径为,则
在中,有,
即
解得
故选:D
6.答案:
解析:作于C,
的半径为4,
,
,
,
在直角中,.
故答案为:.
7.答案:/厘米
解析:连接,如图所示:
由题意知,,,
∵,
∴,
设的半径为,则,,
在中,,
,
解得:,
∴此管件的直径为,
故答案为:.
8.答案:
解析:如图所示,连接AO,过点O作,垂足为C.
,.
.
最大深度为.
答:油的最大深度为.
一、知识预习
1.圆是轴对称图形,任何一条直径所在直线都是圆的对称轴.
2.垂直于弦的直径 弦,并且 弦所对的两条弧.
符号语言:
∵①CD是直径,②CD⊥AB
∴③AE= ,④= ,⑤= .
3.平分弦(不是直径)的直径 于弦,并且 弦所对的两条弧.
符号语言:
∵①CD是直径 ②AE=BE且AB不是直径
∴③CD⊥ ,④= ,⑤=
二、自我检测
1.如图所示是一个单心圆曲隧道的截面,若隧道单心圆的半径的长是,净高为,则此路面宽为( ).
A.7 B.8 C.9 D.10
2.如图,在中,弦的长为8,圆心O到的距离,则的半径长为( )
A.4 B. C.5 D.
3.如图,在半径为5cm的中,弦,于点C,则 ( )
A.3cm B.4cm C.5cm D.6cm
4.如图,已知的半径为,且的弦垂直平分半径,则( )
A. B. C. D.
5.唐代李皋发明了“桨轮船”,这种船是原始形态的轮船,是近代明轮航行模式之先导,如图,某桨轮船的轮子被水面截得的弦长,轮子的吃水深度为,则该浆轮船的轮子半径为( )
A. B. C. D.
6.如图,的半径为4,是的弦,若,则的长为______.
7.一个圆柱形管件,其横截面如图所示,管内存有一些水(阴影部分),测得水面宽为,水的最大深度为,则此圆的直径为___________.
8.往直径为的圆柱形油槽内装入一些油以后,截面如图所示.若油面宽,求油的最大深度.
答案以及解析
一、知识预习
2. 平分 平分 BE
3. 垂直 平分 AB
二、自我检测
1.答案:B
解析:根据题意得到,
在中,,
,
故选B.
2.答案:B
解析:在中,弦的长为8,圆心O到的距离,
,,
在中,,
故选:B.
3.答案:A
解析:连接,
,
,
,,
在中,,
,.
故选:A.
4.答案:C
解析:如图所示,
∵的半径为,
∴,
∵的弦垂直平分半径,
∴,,
∴,
∴.
故选:C.
5.答案:D
解析:设半径为,则
在中,有,
即
解得
故选:D
6.答案:
解析:作于C,
的半径为4,
,
,
,
在直角中,.
故答案为:.
7.答案:/厘米
解析:连接,如图所示:
由题意知,,,
∵,
∴,
设的半径为,则,,
在中,,
,
解得:,
∴此管件的直径为,
故答案为:.
8.答案:
解析:如图所示,连接AO,过点O作,垂足为C.
,.
.
最大深度为.
答:油的最大深度为.
同课章节目录
