(21)正多边形和圆—九年级数学人教版上册课前导学(含答案 )
文档属性
| 名称 | (21)正多边形和圆—九年级数学人教版上册课前导学(含答案 ) |  | |
| 格式 | docx | ||
| 文件大小 | 534.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-11 21:49:33 | ||
图片预览

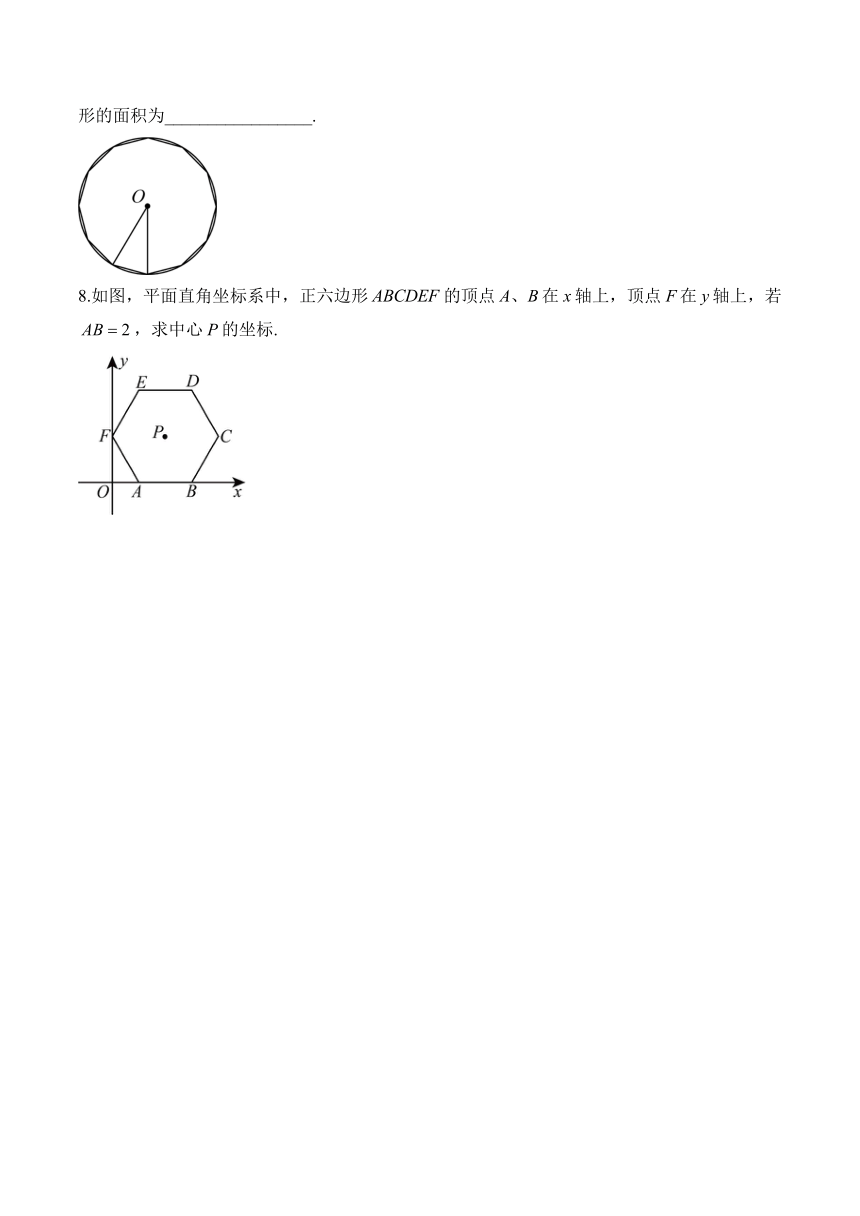
文档简介
(21)正多边形和圆—九年级数学人教版上册课前导学
一、知识预习
1.正多边形:各边 、各角也 的多边形是正多边形.
2.圆内接正多边形:把圆分成等份,依次连接各分点得到的多边形就是这个圆的 ,这个圆就是这个 .
3.与正多边形有关的概念
名称 定义
中心 一个正多边形的外接圆的圆心叫做这个正多边形的中心.
半径 正多边形的 叫做正多边形的半径.
中心角 正多边形每一边所对的 叫做正多边形的中心角.
边心距 正多边形的 到正多边形的一边的距离叫做正多边形的边心距.
二、自我检测
1.若正多边形的一个外角为,则这个正多边形的中心角的度数是( )
A. B. C. D.
2.历史上,我国魏晋时期数学家刘徽(公元263年左右)首创“割圆术”,估算圆周率近似为.实际上,由圆的周长,可得,即求圆周率的问题在某种意义上就可归结为求圆的周长,而圆的周长C是可以用圆内接正多边形的周长来近似代替的,因为当圆的内接正多边形的边数成倍增加时,它的周长就越来越接近圆的周长.如图,的半径为1,若以圆内接正六边形的周长近似估计的周长,可得的估计值为( )
A. B. C. D.3
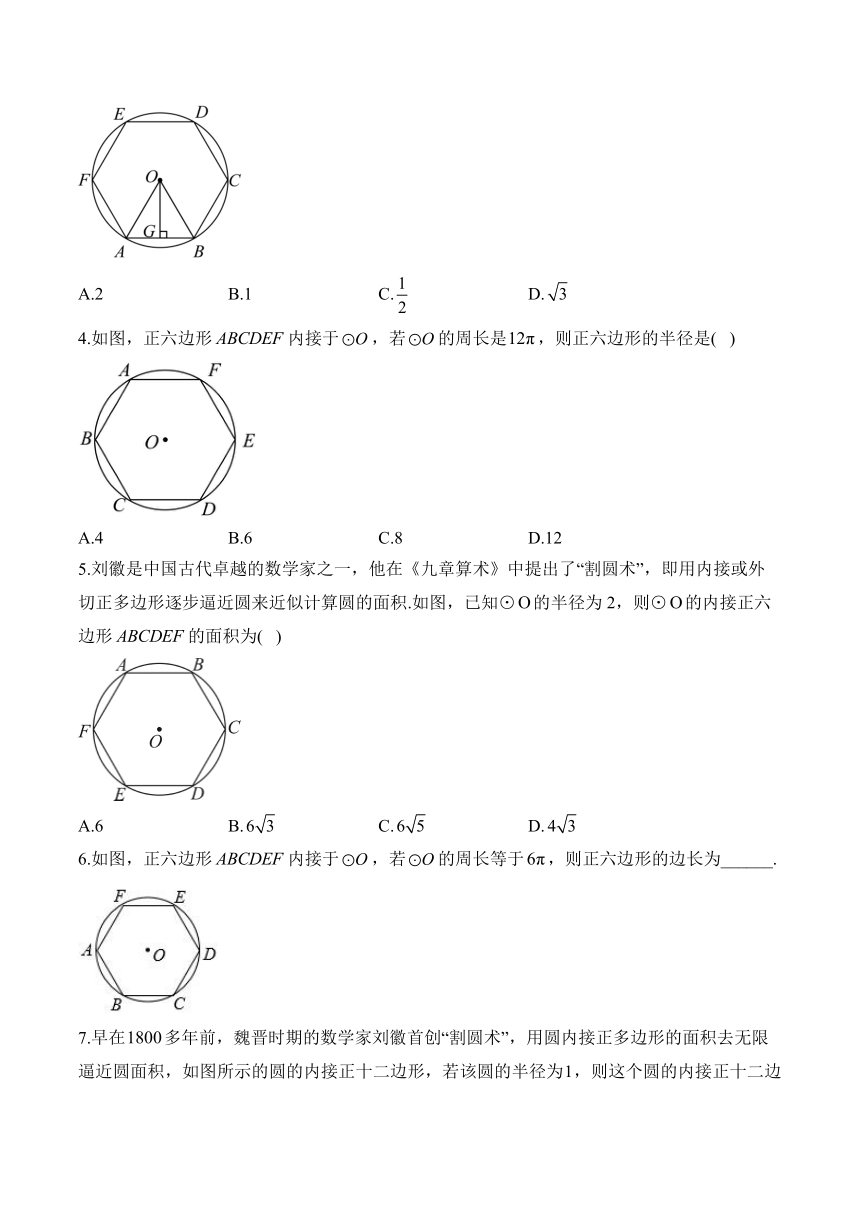
3.如图,的半径为2,正六边形内接于,则这个正六边形的边心距的长为( )
A.2 B.1 C. D.
4.如图,正六边形内接于,若的周长是,则正六边形的半径是( )
A.4 B.6 C.8 D.12
5.刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积.如图,已知⊙的半径为2,则⊙的内接正六边形的面积为( )
A.6 B. C. D.
6.如图,正六边形内接于,若的周长等于,则正六边形的边长为______.
7.早在多年前,魏晋时期的数学家刘徽首创“割圆术”,用圆内接正多边形的面积去无限逼近圆面积,如图所示的圆的内接正十二边形,若该圆的半径为,则这个圆的内接正十二边形的面积为_________________.
8.如图,平面直角坐标系中,正六边形的顶点A、B在x轴上,顶点F在y轴上,若,求中心P的坐标.
答案以及解析
一、知识预习
1.相等 相等
2.内接正多边形 正多边形的外接圆
3.外接圆的半径 圆心角 中心
二、自我检测
1.答案:C
解析:正多边形的一个外角为,
正多边形的边数为,
这个正多边形的中心角的度数是,
故选:C.
2.答案:D
解析:如图,
正六边形的中心角,,
为等边三角形,
,
正六边形的周长为,
,
,
故选:D
3.答案:D
解析:六边形为正六边形,
,
,
为等边三角形,
,
,
,
,
故选:D.
4.答案:B
解析:连接、,如图:
的周长等于,
的半径,
六边形是正六边形,
,
是等边三角形,
,
即正六边形的半径为6,
故答案为:6.
5.答案:B
解析:如图,连接、
由题意可得:
∵
∴为等边三角形,
∴
过点作于点,则
在R中,
∴
∴⊙的面积约为
故选:B.
6.答案:3
解析:连接正六边形的对角线,如图所示:
正六边形内接于,若的周长等于,
直径为,且正六边形的边长为,
的周长等于,解得,
正六边形的边长为,
故答案为:.
7.答案:
解析:如图所示,过点A作的垂线,交于点N.
根据题意可知,,则
.
.
这个圆的内接正十二边形的面积.
故答案为:3.
8.答案:
解析:连接、,过点P作轴于Q,
六边形是正六边形,,
,,,,
,是等边三角形,,
,,,
,
,
中心P的坐标为.
一、知识预习
1.正多边形:各边 、各角也 的多边形是正多边形.
2.圆内接正多边形:把圆分成等份,依次连接各分点得到的多边形就是这个圆的 ,这个圆就是这个 .
3.与正多边形有关的概念
名称 定义
中心 一个正多边形的外接圆的圆心叫做这个正多边形的中心.
半径 正多边形的 叫做正多边形的半径.
中心角 正多边形每一边所对的 叫做正多边形的中心角.
边心距 正多边形的 到正多边形的一边的距离叫做正多边形的边心距.
二、自我检测
1.若正多边形的一个外角为,则这个正多边形的中心角的度数是( )
A. B. C. D.
2.历史上,我国魏晋时期数学家刘徽(公元263年左右)首创“割圆术”,估算圆周率近似为.实际上,由圆的周长,可得,即求圆周率的问题在某种意义上就可归结为求圆的周长,而圆的周长C是可以用圆内接正多边形的周长来近似代替的,因为当圆的内接正多边形的边数成倍增加时,它的周长就越来越接近圆的周长.如图,的半径为1,若以圆内接正六边形的周长近似估计的周长,可得的估计值为( )
A. B. C. D.3
3.如图,的半径为2,正六边形内接于,则这个正六边形的边心距的长为( )
A.2 B.1 C. D.
4.如图,正六边形内接于,若的周长是,则正六边形的半径是( )
A.4 B.6 C.8 D.12
5.刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积.如图,已知⊙的半径为2,则⊙的内接正六边形的面积为( )
A.6 B. C. D.
6.如图,正六边形内接于,若的周长等于,则正六边形的边长为______.
7.早在多年前,魏晋时期的数学家刘徽首创“割圆术”,用圆内接正多边形的面积去无限逼近圆面积,如图所示的圆的内接正十二边形,若该圆的半径为,则这个圆的内接正十二边形的面积为_________________.
8.如图,平面直角坐标系中,正六边形的顶点A、B在x轴上,顶点F在y轴上,若,求中心P的坐标.
答案以及解析
一、知识预习
1.相等 相等
2.内接正多边形 正多边形的外接圆
3.外接圆的半径 圆心角 中心
二、自我检测
1.答案:C
解析:正多边形的一个外角为,
正多边形的边数为,
这个正多边形的中心角的度数是,
故选:C.
2.答案:D
解析:如图,
正六边形的中心角,,
为等边三角形,
,
正六边形的周长为,
,
,
故选:D
3.答案:D
解析:六边形为正六边形,
,
,
为等边三角形,
,
,
,
,
故选:D.
4.答案:B
解析:连接、,如图:
的周长等于,
的半径,
六边形是正六边形,
,
是等边三角形,
,
即正六边形的半径为6,
故答案为:6.
5.答案:B
解析:如图,连接、
由题意可得:
∵
∴为等边三角形,
∴
过点作于点,则
在R中,
∴
∴⊙的面积约为
故选:B.
6.答案:3
解析:连接正六边形的对角线,如图所示:
正六边形内接于,若的周长等于,
直径为,且正六边形的边长为,
的周长等于,解得,
正六边形的边长为,
故答案为:.
7.答案:
解析:如图所示,过点A作的垂线,交于点N.
根据题意可知,,则
.
.
这个圆的内接正十二边形的面积.
故答案为:3.
8.答案:
解析:连接、,过点P作轴于Q,
六边形是正六边形,,
,,,,
,是等边三角形,,
,,,
,
,
中心P的坐标为.
同课章节目录
