(22)弧长和扇形面积—九年级数学人教版上册课前导学(含答案)
文档属性
| 名称 | (22)弧长和扇形面积—九年级数学人教版上册课前导学(含答案) | 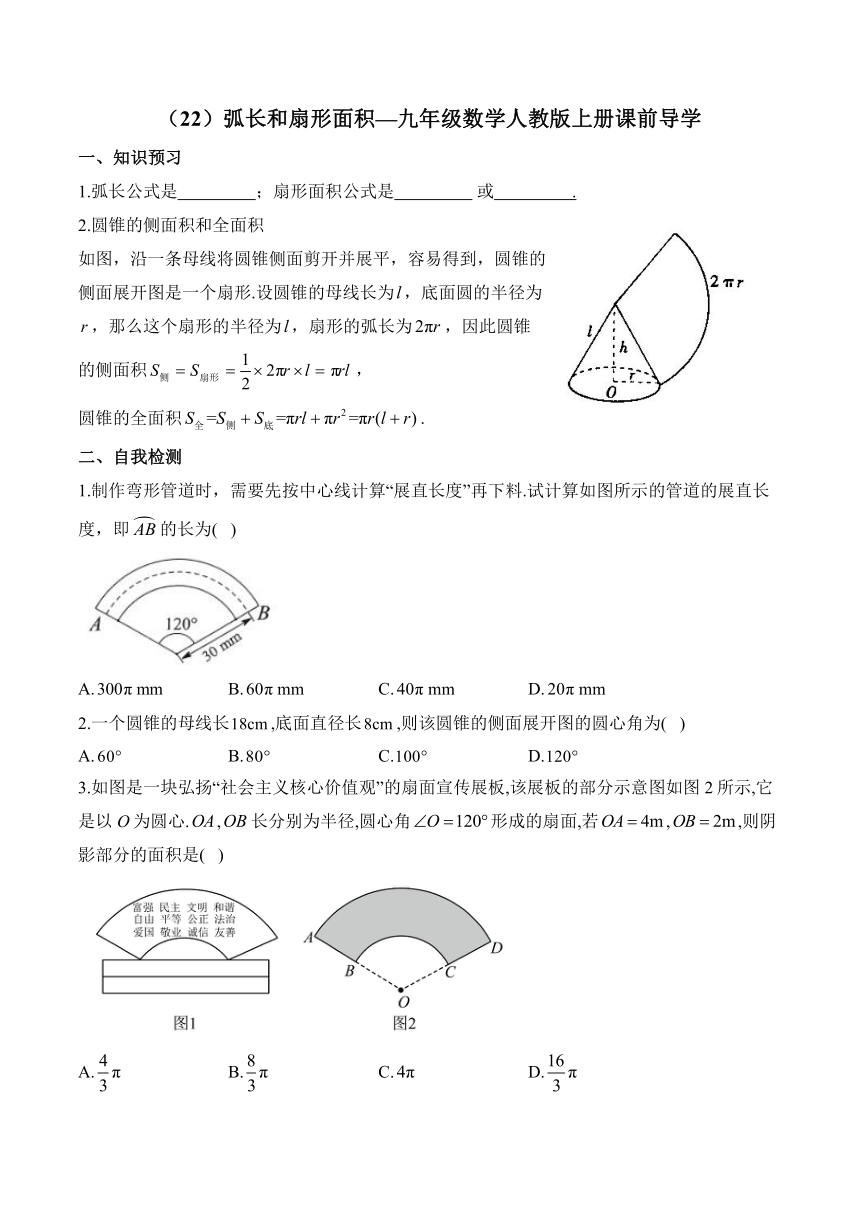 | |
| 格式 | docx | ||
| 文件大小 | 422.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-11 21:50:05 | ||
图片预览


文档简介
(22)弧长和扇形面积—九年级数学人教版上册课前导学
一、知识预习
1.弧长公式是 ;扇形面积公式是 或 .
2.圆锥的侧面积和全面积
如图,沿一条母线将圆锥侧面剪开并展平,容易得到,圆锥的侧面展开图是一个扇形.设圆锥的母线长为,底面圆的半径为,那么这个扇形的半径为,扇形的弧长为,因此圆锥的侧面积,
圆锥的全面积.
二、自我检测
1.制作弯形管道时,需要先按中心线计算“展直长度”再下料.试计算如图所示的管道的展直长度,即的长为( )
A. B. C. D.
2.一个圆锥的母线长,底面直径长,则该圆锥的侧面展开图的圆心角为( )
A. B. C. D.
3.如图是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心.,长分别为半径,圆心角形成的扇面,若,,则阴影部分的面积是( )
A. B. C. D.
4.如图,已知的半径为6,,是的弦,若,则弧的长是( )
A. B. C. D.
5.如图,半径为5的扇形中,,C是上一点,,,垂足分别为D,E,若,则图中阴影部分面积为( )
A. B. C. D.
6.一个扇形的半径为4,圆心角为,则此扇形的弧长为____________.(结果保留)
7.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形.若母线长l为,扇形的圆心角为,则圆锥的底面圆的半径r为______.
8.如图:O点是半圆的圆心,半圆的直径是4厘米,C、D是半圆弧上的三等分点,求图中阴影部分的面积.
答案以及解析
一、知识预习
1.
二、自我检测
1.答案:D
解析:,,所以
的长.
因此,管道的展直长度约为.
故选:D.
2.答案:B
解析:设该圆锥的侧面展开图的圆心角的度数为,
依题意得:,
解得:,
∴该圆锥的侧面展开图的圆心角为.
故选:B.
3.答案:C
解析:圆心角,,,
∴,
∴,
故选:C.
4.答案:C
解析:如图,连接OA,OC,
,
弧AC的长为:,
故选:C.
5.答案:B
解析:如图所示,连接,
∵,,,
∴四边形是矩形,
∵,
∴四边形是正方形,
∴,,
∴图中阴影部分面积,
故选:B.
6.答案:
解析:,
故答案为.
7.答案:2
解析:由题意得:母线长l为,,
,
∴,
故答案为:2.
8.答案:平方厘米
解析:连接、、,
因为C、D是半圆弧上的三等分点,所以圆心角
分析可知,三角形和三角形等底等高,
故阴影部分的面积=扇形的面积(平方厘米)
答:阴影部分的面积是平方厘米.
一、知识预习
1.弧长公式是 ;扇形面积公式是 或 .
2.圆锥的侧面积和全面积
如图,沿一条母线将圆锥侧面剪开并展平,容易得到,圆锥的侧面展开图是一个扇形.设圆锥的母线长为,底面圆的半径为,那么这个扇形的半径为,扇形的弧长为,因此圆锥的侧面积,
圆锥的全面积.
二、自我检测
1.制作弯形管道时,需要先按中心线计算“展直长度”再下料.试计算如图所示的管道的展直长度,即的长为( )
A. B. C. D.
2.一个圆锥的母线长,底面直径长,则该圆锥的侧面展开图的圆心角为( )
A. B. C. D.
3.如图是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心.,长分别为半径,圆心角形成的扇面,若,,则阴影部分的面积是( )
A. B. C. D.
4.如图,已知的半径为6,,是的弦,若,则弧的长是( )
A. B. C. D.
5.如图,半径为5的扇形中,,C是上一点,,,垂足分别为D,E,若,则图中阴影部分面积为( )
A. B. C. D.
6.一个扇形的半径为4,圆心角为,则此扇形的弧长为____________.(结果保留)
7.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形.若母线长l为,扇形的圆心角为,则圆锥的底面圆的半径r为______.
8.如图:O点是半圆的圆心,半圆的直径是4厘米,C、D是半圆弧上的三等分点,求图中阴影部分的面积.
答案以及解析
一、知识预习
1.
二、自我检测
1.答案:D
解析:,,所以
的长.
因此,管道的展直长度约为.
故选:D.
2.答案:B
解析:设该圆锥的侧面展开图的圆心角的度数为,
依题意得:,
解得:,
∴该圆锥的侧面展开图的圆心角为.
故选:B.
3.答案:C
解析:圆心角,,,
∴,
∴,
故选:C.
4.答案:C
解析:如图,连接OA,OC,
,
弧AC的长为:,
故选:C.
5.答案:B
解析:如图所示,连接,
∵,,,
∴四边形是矩形,
∵,
∴四边形是正方形,
∴,,
∴图中阴影部分面积,
故选:B.
6.答案:
解析:,
故答案为.
7.答案:2
解析:由题意得:母线长l为,,
,
∴,
故答案为:2.
8.答案:平方厘米
解析:连接、、,
因为C、D是半圆弧上的三等分点,所以圆心角
分析可知,三角形和三角形等底等高,
故阴影部分的面积=扇形的面积(平方厘米)
答:阴影部分的面积是平方厘米.
同课章节目录
