鲁教版2024-2025学年度第一学期九年级数学 1.2 反比例函数的图像和性质 分层练习(含答案)
文档属性
| 名称 | 鲁教版2024-2025学年度第一学期九年级数学 1.2 反比例函数的图像和性质 分层练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 267.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-12 00:00:00 | ||
图片预览


文档简介
鲁教版2024-2025学年度第一学期九年级数学1.2 反比例函数的图像和性质
同步测试
一、单选题
1.在反比例函数 的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k>1 B.k>0 C.k≥1 D.k<1
2.若A(1,y1),B(2,y2)两点都在反比例函数y= 的图象上,则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.无法确定
3.反比例函数 的图象位于( )
A.第一、二象限 B.第三、四象限
C.第一、象限 D.第二、四象限
4.如图已知双曲线 上有一点 ,过A作AB垂直x轴于点B,连接OA,则 的面积为( )
A.1 B.2 C.3 D.6
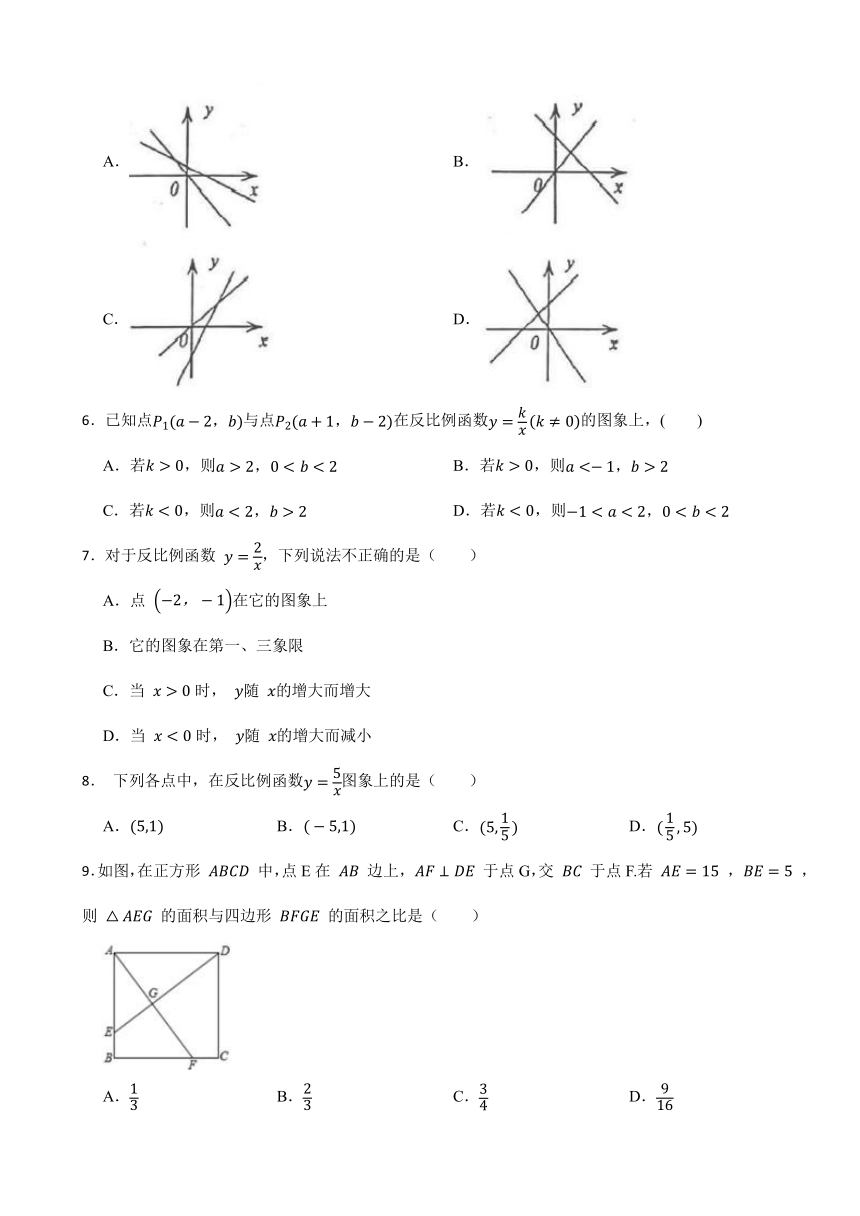
5.一次函数与正比例函数(,是常数,且)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
6.已知点与点在反比例函数的图象上,( )
A.若,则 B.若,则
C.若,则 D.若,则
7.对于反比例函数 ,下列说法不正确的是( )
A.点 在它的图象上
B.它的图象在第一、三象限
C.当 时, 随 的增大而增大
D.当 时, 随 的增大而减小
8. 下列各点中,在反比例函数图象上的是( )
A. B. C. D.
9.如图,在正方形 中,点E在 边上, 于点G,交 于点F.若 , ,则 的面积与四边形 的面积之比是( )
A. B. C. D.
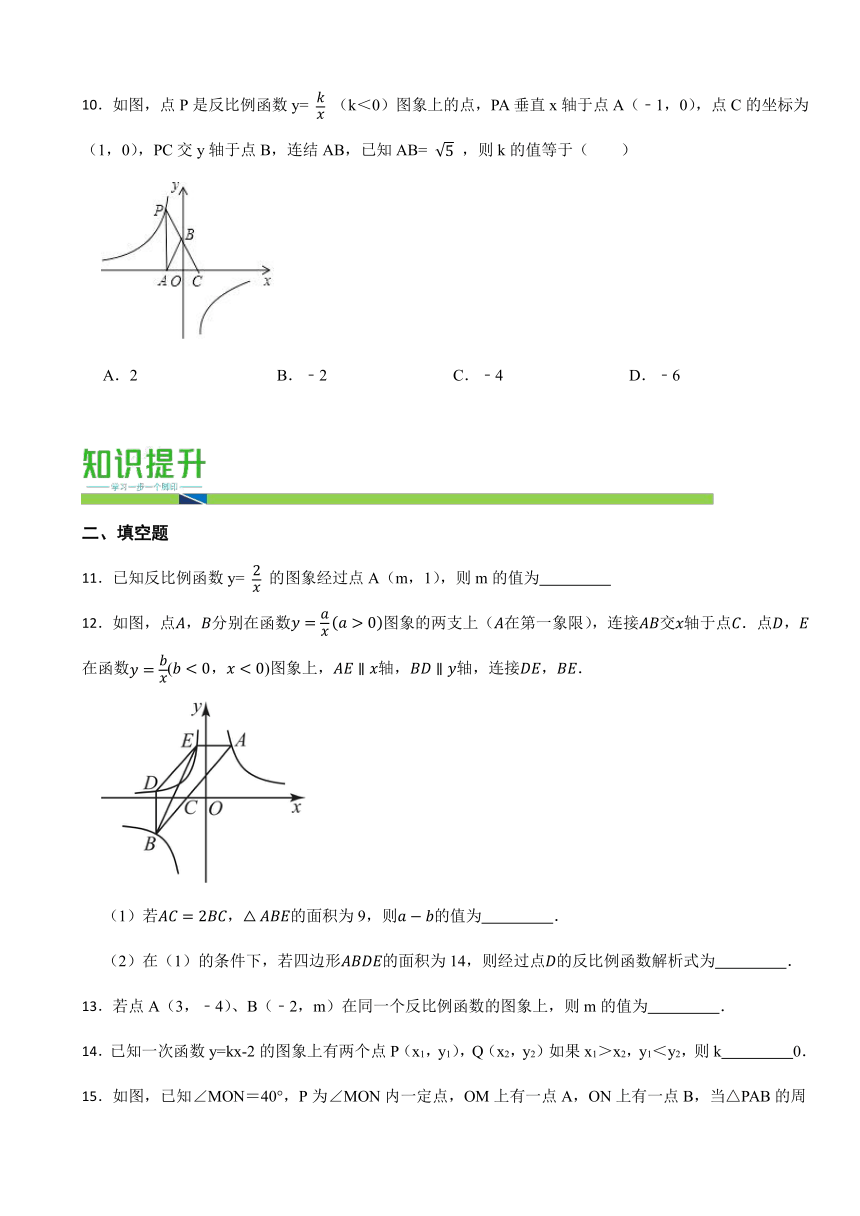
10.如图,点P是反比例函数y= (k<0)图象上的点,PA垂直x轴于点A(﹣1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB= ,则k的值等于( )
A.2 B.﹣2 C.﹣4 D.﹣6
二、填空题
11.已知反比例函数y= 的图象经过点A(m,1),则m的值为
12.如图,点,分别在函数图象的两支上(在第一象限),连接交轴于点.点,在函数(,)图象上,轴,轴,连接,.
(1)若,的面积为9,则的值为 .
(2)在(1)的条件下,若四边形的面积为14,则经过点的反比例函数解析式为 .
13.若点A(3,﹣4)、B(﹣2,m)在同一个反比例函数的图象上,则m的值为 .
14.已知一次函数y=kx-2的图象上有两个点P(x1,y1),Q(x2,y2)如果x1>x2,y1<y2,则k 0.
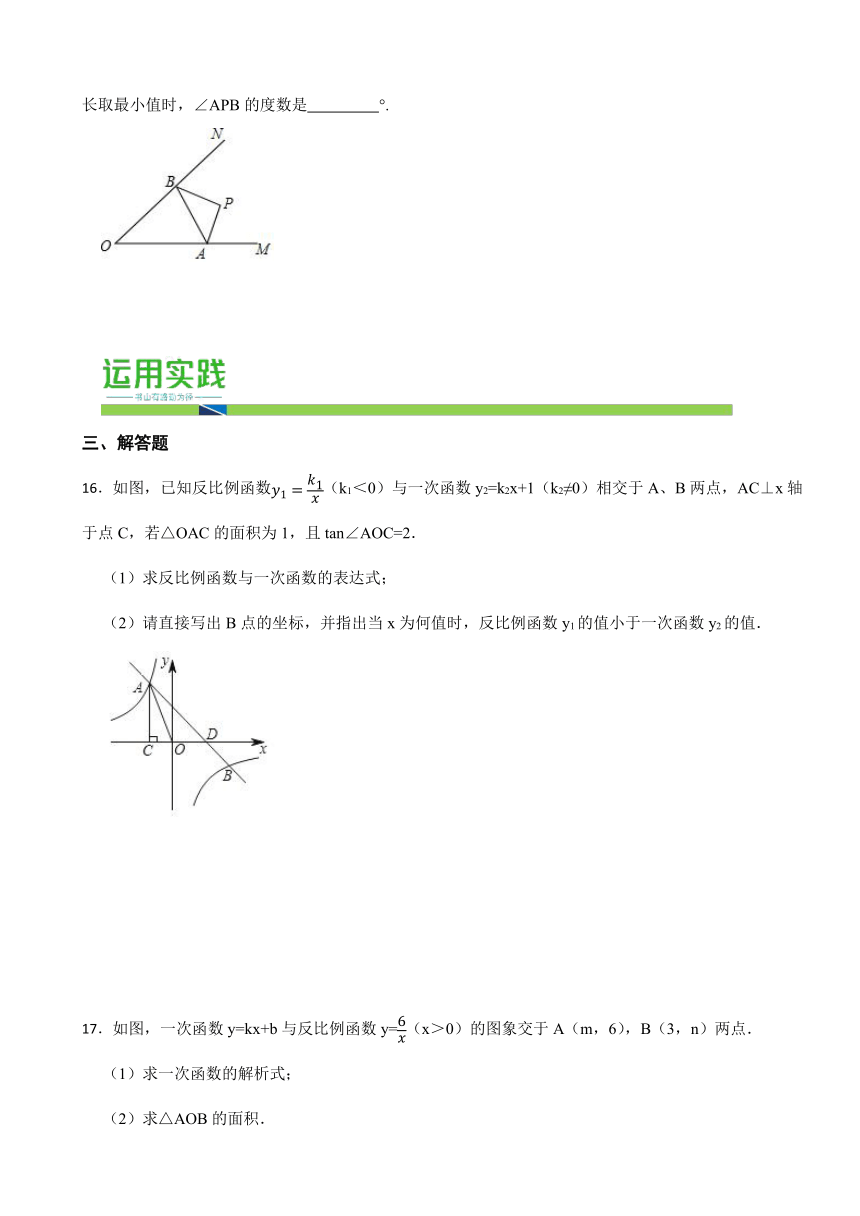
15.如图,已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,∠APB的度数是 °.
三、解答题
16.如图,已知反比例函数(k1<0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C,若△OAC的面积为1,且tan∠AOC=2.
(1)求反比例函数与一次函数的表达式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值小于一次函数y2的值.
17.如图,一次函数y=kx+b与反比例函数y=(x>0)的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)求△AOB的面积.
如图,A为反比例函数(k不为0)上一点,连接OA,过A点作AB⊥x轴于B,若OA=5,AB=4.求该反比例函数的解析式.
已知反比例函数 ,当 时,y随x的增大而减小,求正整数m的值.
20.如图,已知直线y=x与反比例函数y=(k>0)的图象交于A,B两点,且点A的横坐标为4.
(1)求k的值.
(2)若反比例函数y=的图象上一点C的纵坐标为8,求△AOC的面积.
(3)若过原点O的另一条直线l交反比例函数y= (k>0)的图象于P,Q两点(点P在第一象限),以A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.
21.如图是函数 与函数 在第一象限内的图象,点P是 的图象上一动点,PA⊥x轴于点A,交 的图象于点C, PB⊥y轴于点B,交 的图象于点D.
(1)求证:D是BP的中点;
(2)求出四边形ODPC的面积.
22.如图,一次函数y=x+5的图象与反比例函数(k为常数且k≠0)的图象交于A(﹣2,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=S△BOC,求点P的坐标.
(3)直接写出x+5﹣<0的解集.
23.实验数据显示,一般成人喝50毫升某品牌白酒后,血液中酒精含量y(毫克/百毫升)与时间x(时)变化的图象如图(图象由线段与部分双曲线AB组成)所示.国家规定,车辆驾驶人员血液中的酒精含量大于或等于20(毫克/百毫升)时属于“酒后驾驶”,不能驾车上路.
(1)求部分双曲线的函数表达式;
(2)参照上述数学模型,假设某驾驶员晚上在家喝完50毫升该品牌白酒,第二天早上能否驾车去上班?请说明理由.
24.如图:已知A(﹣4,n)、B(2,﹣4)是一次函数y1=kx+b的图象与反比例函数y2=的图象的两个交点.
(1)求反比例函数和一次函数的解折式.
(2)求直线AB与x轴的交点C的坐标及△AOB的面积.
(3)求不等式y1<y2的解集(请直接写出答案).
1.A
2.C
3.D
4.C
5.A
6.D
7.C
8.A
9.D
10.C
11.2
12.12;
13.6
14.<
15.100
16.解:(1)∵点A在的图象上,S△ACO=1,
∴|k1|=2×1=2,
又∵k1<0,
∴k1=﹣2.
∴反比例函数的表达式为 .
设点A(a,),a<0,
∵在Rt△AOC中, ,
∴,
∵a<0,
∴a=﹣1.
∴A(﹣1,2).
∵点A(﹣1,2)在y2=k2x+1上,
∴2=﹣k2+1,
∴k2=﹣1.
∴一次函数的表达式为y2=﹣x+1.
(2)点B坐标为(2,﹣1),
观察图象可知,当x<﹣1或0<x<2时,
反比例函数y1的值小于一次函数y2的值.
17.解:(1)把点(m,6),B(3,n)分别代入y=(x>0)得m=1,n=2,
∴A点坐标为(1,6),B点坐标为(3,2),
把A(1,6),B(3,2)分别代入y=kx+b得,解得,
∴一次函数解析式为y=﹣2x+8;
(2)分别过点A、B作AE⊥x轴,BC⊥x轴,垂足分别是E、C点.直线AB交x轴于D点.
令﹣2x+8=0,得x=4,即D(4,0).
∵A(1,6),B(3,2),
∴AE=6,BC=2,
∴S△AOB=S△AOD﹣S△BOD=×4×6﹣×4×2=8.
18.在中,
过
19.解:∵对于反比例函数 ,当 时,y随x的增大而减小,
∴ ,
解得: ,
∵m为正整数,
∴m=1.
20.(1)8(2)15(3) (2,4)或(8,1)
21.(1)证明:因为点P(x,y)在反比例函数,则可设P(x,).则BP=x.
∵PB⊥y轴,
∴点D的纵坐标与点P的纵坐标相等,则D的纵坐标是,
又∵点D在反比例函数,
∴D(,),
则BD=,
BD=BP,
即D是BP的中点.
(2)解:S四边形ODPC=S四边形OAPB-S△OBD-S△OAC=6--=3.
22.(1)
(2)P(﹣)或()
(3)x<﹣3或﹣2<x<0
23.(1);
(2)第二天早上不能驾车去上班.
24.解:(1)①将B(2,﹣4)代入y2=,可得=﹣4,
解得m=﹣8,
∴y2=,
②当x=﹣4时,y=,
∴A(﹣4,2),
又将A(﹣4,2)、B(2,﹣4)代入y1=kx+b可得:
,
解得,
∴y1=﹣x﹣2;
(2)令y1=0可得:﹣x﹣2=0,
∴x=﹣2,
∴C(﹣2,0),
S△AOB=S△AOC+S△BOC=×2×2+×2×4=2+4=6,
(3)当﹣4<x<0或x>2时,y1<y2.
同步测试
一、单选题
1.在反比例函数 的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k>1 B.k>0 C.k≥1 D.k<1
2.若A(1,y1),B(2,y2)两点都在反比例函数y= 的图象上,则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.无法确定
3.反比例函数 的图象位于( )
A.第一、二象限 B.第三、四象限
C.第一、象限 D.第二、四象限
4.如图已知双曲线 上有一点 ,过A作AB垂直x轴于点B,连接OA,则 的面积为( )
A.1 B.2 C.3 D.6
5.一次函数与正比例函数(,是常数,且)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
6.已知点与点在反比例函数的图象上,( )
A.若,则 B.若,则
C.若,则 D.若,则
7.对于反比例函数 ,下列说法不正确的是( )
A.点 在它的图象上
B.它的图象在第一、三象限
C.当 时, 随 的增大而增大
D.当 时, 随 的增大而减小
8. 下列各点中,在反比例函数图象上的是( )
A. B. C. D.
9.如图,在正方形 中,点E在 边上, 于点G,交 于点F.若 , ,则 的面积与四边形 的面积之比是( )
A. B. C. D.
10.如图,点P是反比例函数y= (k<0)图象上的点,PA垂直x轴于点A(﹣1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB= ,则k的值等于( )
A.2 B.﹣2 C.﹣4 D.﹣6
二、填空题
11.已知反比例函数y= 的图象经过点A(m,1),则m的值为
12.如图,点,分别在函数图象的两支上(在第一象限),连接交轴于点.点,在函数(,)图象上,轴,轴,连接,.
(1)若,的面积为9,则的值为 .
(2)在(1)的条件下,若四边形的面积为14,则经过点的反比例函数解析式为 .
13.若点A(3,﹣4)、B(﹣2,m)在同一个反比例函数的图象上,则m的值为 .
14.已知一次函数y=kx-2的图象上有两个点P(x1,y1),Q(x2,y2)如果x1>x2,y1<y2,则k 0.
15.如图,已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,∠APB的度数是 °.
三、解答题
16.如图,已知反比例函数(k1<0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C,若△OAC的面积为1,且tan∠AOC=2.
(1)求反比例函数与一次函数的表达式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值小于一次函数y2的值.
17.如图,一次函数y=kx+b与反比例函数y=(x>0)的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)求△AOB的面积.
如图,A为反比例函数(k不为0)上一点,连接OA,过A点作AB⊥x轴于B,若OA=5,AB=4.求该反比例函数的解析式.
已知反比例函数 ,当 时,y随x的增大而减小,求正整数m的值.
20.如图,已知直线y=x与反比例函数y=(k>0)的图象交于A,B两点,且点A的横坐标为4.
(1)求k的值.
(2)若反比例函数y=的图象上一点C的纵坐标为8,求△AOC的面积.
(3)若过原点O的另一条直线l交反比例函数y= (k>0)的图象于P,Q两点(点P在第一象限),以A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.
21.如图是函数 与函数 在第一象限内的图象,点P是 的图象上一动点,PA⊥x轴于点A,交 的图象于点C, PB⊥y轴于点B,交 的图象于点D.
(1)求证:D是BP的中点;
(2)求出四边形ODPC的面积.
22.如图,一次函数y=x+5的图象与反比例函数(k为常数且k≠0)的图象交于A(﹣2,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=S△BOC,求点P的坐标.
(3)直接写出x+5﹣<0的解集.
23.实验数据显示,一般成人喝50毫升某品牌白酒后,血液中酒精含量y(毫克/百毫升)与时间x(时)变化的图象如图(图象由线段与部分双曲线AB组成)所示.国家规定,车辆驾驶人员血液中的酒精含量大于或等于20(毫克/百毫升)时属于“酒后驾驶”,不能驾车上路.
(1)求部分双曲线的函数表达式;
(2)参照上述数学模型,假设某驾驶员晚上在家喝完50毫升该品牌白酒,第二天早上能否驾车去上班?请说明理由.
24.如图:已知A(﹣4,n)、B(2,﹣4)是一次函数y1=kx+b的图象与反比例函数y2=的图象的两个交点.
(1)求反比例函数和一次函数的解折式.
(2)求直线AB与x轴的交点C的坐标及△AOB的面积.
(3)求不等式y1<y2的解集(请直接写出答案).
1.A
2.C
3.D
4.C
5.A
6.D
7.C
8.A
9.D
10.C
11.2
12.12;
13.6
14.<
15.100
16.解:(1)∵点A在的图象上,S△ACO=1,
∴|k1|=2×1=2,
又∵k1<0,
∴k1=﹣2.
∴反比例函数的表达式为 .
设点A(a,),a<0,
∵在Rt△AOC中, ,
∴,
∵a<0,
∴a=﹣1.
∴A(﹣1,2).
∵点A(﹣1,2)在y2=k2x+1上,
∴2=﹣k2+1,
∴k2=﹣1.
∴一次函数的表达式为y2=﹣x+1.
(2)点B坐标为(2,﹣1),
观察图象可知,当x<﹣1或0<x<2时,
反比例函数y1的值小于一次函数y2的值.
17.解:(1)把点(m,6),B(3,n)分别代入y=(x>0)得m=1,n=2,
∴A点坐标为(1,6),B点坐标为(3,2),
把A(1,6),B(3,2)分别代入y=kx+b得,解得,
∴一次函数解析式为y=﹣2x+8;
(2)分别过点A、B作AE⊥x轴,BC⊥x轴,垂足分别是E、C点.直线AB交x轴于D点.
令﹣2x+8=0,得x=4,即D(4,0).
∵A(1,6),B(3,2),
∴AE=6,BC=2,
∴S△AOB=S△AOD﹣S△BOD=×4×6﹣×4×2=8.
18.在中,
过
19.解:∵对于反比例函数 ,当 时,y随x的增大而减小,
∴ ,
解得: ,
∵m为正整数,
∴m=1.
20.(1)8(2)15(3) (2,4)或(8,1)
21.(1)证明:因为点P(x,y)在反比例函数,则可设P(x,).则BP=x.
∵PB⊥y轴,
∴点D的纵坐标与点P的纵坐标相等,则D的纵坐标是,
又∵点D在反比例函数,
∴D(,),
则BD=,
BD=BP,
即D是BP的中点.
(2)解:S四边形ODPC=S四边形OAPB-S△OBD-S△OAC=6--=3.
22.(1)
(2)P(﹣)或()
(3)x<﹣3或﹣2<x<0
23.(1);
(2)第二天早上不能驾车去上班.
24.解:(1)①将B(2,﹣4)代入y2=,可得=﹣4,
解得m=﹣8,
∴y2=,
②当x=﹣4时,y=,
∴A(﹣4,2),
又将A(﹣4,2)、B(2,﹣4)代入y1=kx+b可得:
,
解得,
∴y1=﹣x﹣2;
(2)令y1=0可得:﹣x﹣2=0,
∴x=﹣2,
∴C(﹣2,0),
S△AOB=S△AOC+S△BOC=×2×2+×2×4=2+4=6,
(3)当﹣4<x<0或x>2时,y1<y2.
