人教版2019高中物理选择性必修一2.4 单摆(共22张PPT)
文档属性
| 名称 | 人教版2019高中物理选择性必修一2.4 单摆(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 50.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-10-12 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
§2.4 单 摆
构建模型?
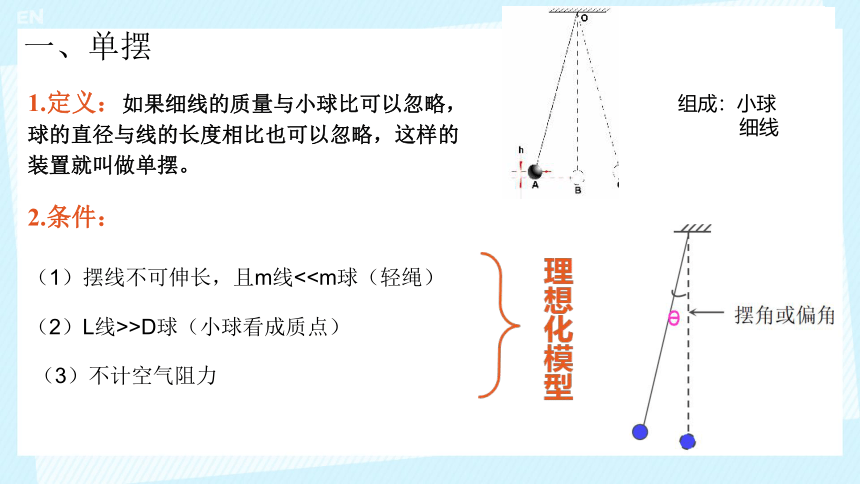
1.定义:如果细线的质量与小球比可以忽略,球的直径与线的长度相比也可以忽略,这样的装置就叫做单摆。
2.条件:
(1)摆线不可伸长,且m线<(2)L线>>D球(小球看成质点)
(3)不计空气阻力
一、单摆
组成:小球
细线
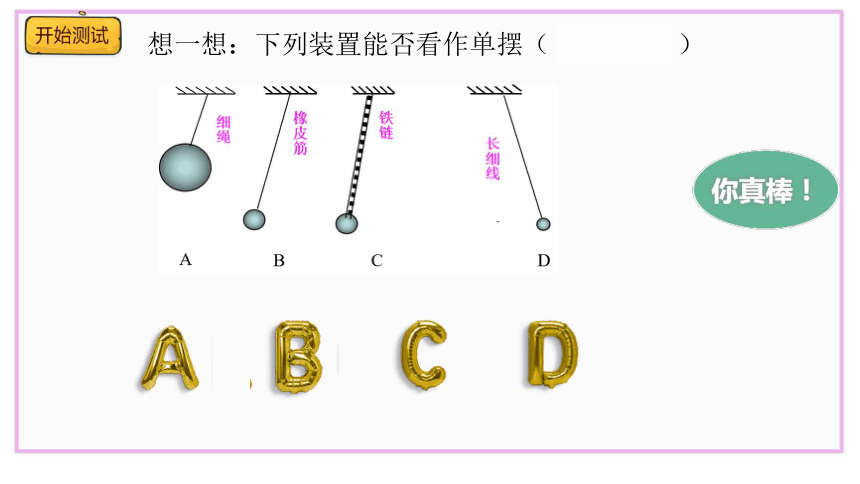
想一想:下列装置能否看作单摆( )
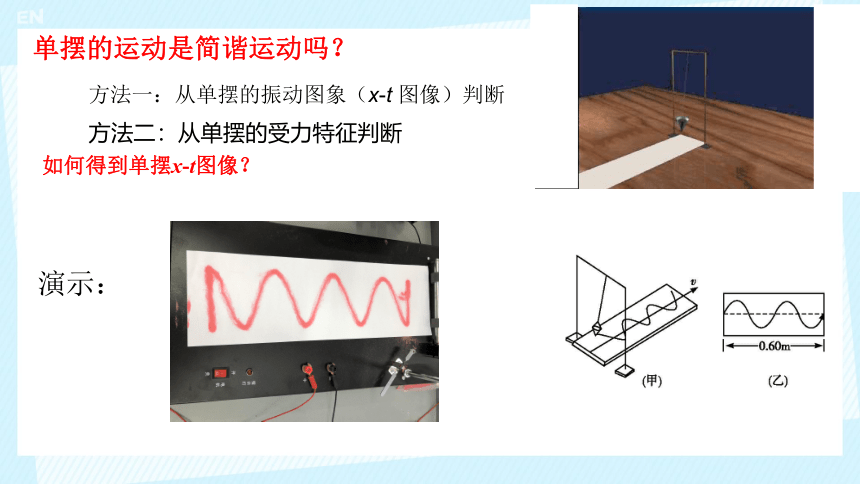
单摆的运动是简谐运动吗?
方法一:从单摆的振动图象(x-t 图像)判断
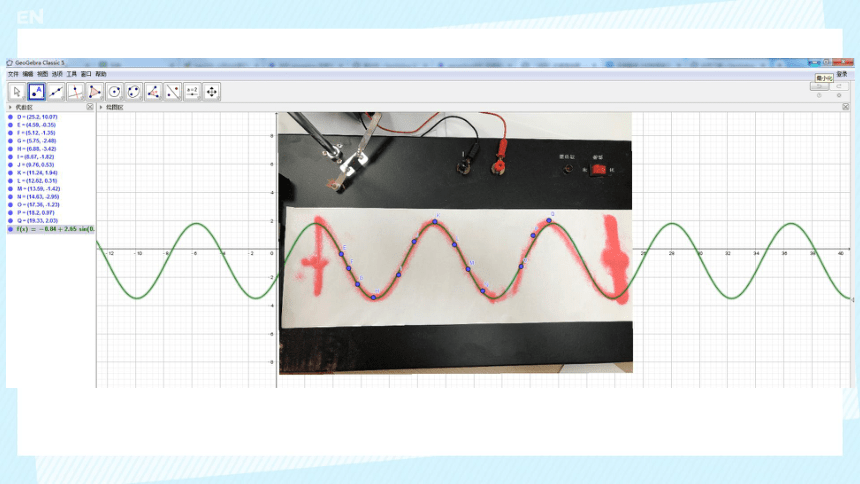
如何得到单摆x-t图像?
演示:
方法二:从单摆的受力特征判断
1.平衡位置:
2.受力分析:
3.回复力来源:
大小:
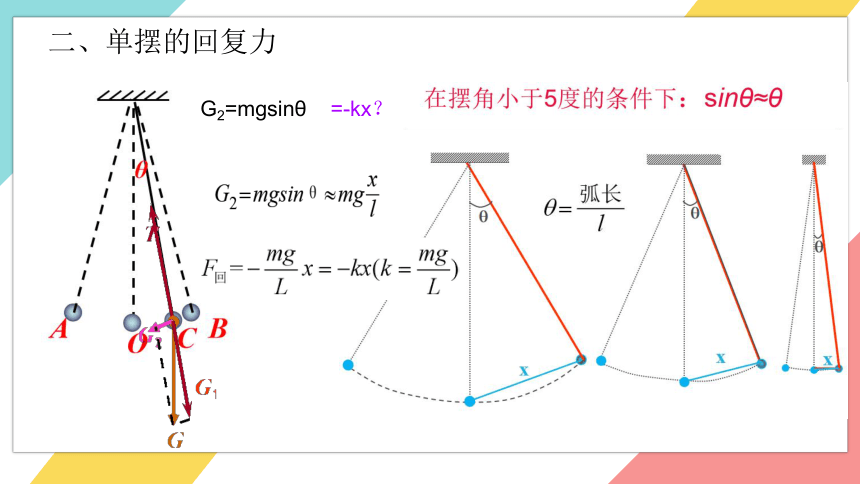
G2=Gsinθ=mg sinθ
方向:
沿切线指向平衡位置
重力沿切线方向的分力G2
最低点O
G2=mgsinθ =-kx?
二、单摆的回复力
猜想?
振幅
质量
摆长
猜想: 单摆摆动的周期与哪些因素有关呢?
三、单摆的周期
单摆的周期
……
控制变量法
单摆周期和振幅、质量、摆长的关系
三、单摆的周期
摆角很小的情况下,单摆做简谐运动的振动周期跟摆长的平方根成正比,跟重力加速度的平方根成反比。与振幅、摆球质量无关。
周期公式:
(1)L为单摆的摆长 L=L 绳+r球
(2)g为当地重力加速度
(3)摆长、重力加速度都一定时周期和频率也一定,通常称为单摆的固有周期和固有频率。
太空中的单摆
摆钟怎么了?
小明家从广州搬到了北京,搬家时把家里的摆钟也带去了。过了几天之后,小明发现摆钟的时间不准确了。校准后,过了几天又出现相同的情况,你知道这是为什么吗?摆钟变快还是变慢了?该怎么调整?
2、如图所示,摆长为L的单摆,原来的周期为T。
现在在悬点O的正下方A点固定一颗钉子,OA=5L/9,
令单摆由平衡位置向左摆动时以A为悬点作简谐振动,
则这个摆完成一次全振动所需的时间是多少?
在摆角很小的条件下:Sinθ≈θ(弧度值)
角度 1° 2° 3° 4° 5° 6° 7° 8° 9° 10°
弧度值 0.0175 0.0349 0.0524 0.0698 0.0873 0.1047 0.1222 0.1396 0.1571 0.1745
正弦值 0.0175 0.0349 0.0524 0.0698 0.0872 0.1045 0.1219 0.1392 0.1564 0.1736
差值 0 0 0 0 0.0001 0.0002 0.0003 0.0004 0.0007 0.0009
§2.4 单 摆
构建模型?
1.定义:如果细线的质量与小球比可以忽略,球的直径与线的长度相比也可以忽略,这样的装置就叫做单摆。
2.条件:
(1)摆线不可伸长,且m线<
(3)不计空气阻力
一、单摆
组成:小球
细线
想一想:下列装置能否看作单摆( )
单摆的运动是简谐运动吗?
方法一:从单摆的振动图象(x-t 图像)判断
如何得到单摆x-t图像?
演示:
方法二:从单摆的受力特征判断
1.平衡位置:
2.受力分析:
3.回复力来源:
大小:
G2=Gsinθ=mg sinθ
方向:
沿切线指向平衡位置
重力沿切线方向的分力G2
最低点O
G2=mgsinθ =-kx?
二、单摆的回复力
猜想?
振幅
质量
摆长
猜想: 单摆摆动的周期与哪些因素有关呢?
三、单摆的周期
单摆的周期
……
控制变量法
单摆周期和振幅、质量、摆长的关系
三、单摆的周期
摆角很小的情况下,单摆做简谐运动的振动周期跟摆长的平方根成正比,跟重力加速度的平方根成反比。与振幅、摆球质量无关。
周期公式:
(1)L为单摆的摆长 L=L 绳+r球
(2)g为当地重力加速度
(3)摆长、重力加速度都一定时周期和频率也一定,通常称为单摆的固有周期和固有频率。
太空中的单摆
摆钟怎么了?
小明家从广州搬到了北京,搬家时把家里的摆钟也带去了。过了几天之后,小明发现摆钟的时间不准确了。校准后,过了几天又出现相同的情况,你知道这是为什么吗?摆钟变快还是变慢了?该怎么调整?
2、如图所示,摆长为L的单摆,原来的周期为T。
现在在悬点O的正下方A点固定一颗钉子,OA=5L/9,
令单摆由平衡位置向左摆动时以A为悬点作简谐振动,
则这个摆完成一次全振动所需的时间是多少?
在摆角很小的条件下:Sinθ≈θ(弧度值)
角度 1° 2° 3° 4° 5° 6° 7° 8° 9° 10°
弧度值 0.0175 0.0349 0.0524 0.0698 0.0873 0.1047 0.1222 0.1396 0.1571 0.1745
正弦值 0.0175 0.0349 0.0524 0.0698 0.0872 0.1045 0.1219 0.1392 0.1564 0.1736
差值 0 0 0 0 0.0001 0.0002 0.0003 0.0004 0.0007 0.0009
