北京市京源学校2024-2025学年第一学期初三数学10月月考试卷(PDF版,无答案)
文档属性
| 名称 | 北京市京源学校2024-2025学年第一学期初三数学10月月考试卷(PDF版,无答案) |

|
|
| 格式 | |||
| 文件大小 | 707.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-10 00:00:00 | ||
图片预览



文档简介
2024-2025 学年初三年级 10 月学科诊断
数学试卷
(满分 120 分,时间 120 分钟)
班级 姓名 学号 成绩
一、选择题(本题共 24 分,每小题 3 分)
第 1- 8 题均有四个选项,符合题意的选项只有一个.
x 2 y x
1.如果 ,那么 的值是( )
y 3 y
1 1 5 5
A. B. C. D.
3 2 3 2
2.抛物线 y=(x﹣1)2 +3的顶点坐标是( )
A.(1,3) B.(﹣1,3) C.(﹣1,﹣3) D.(1,﹣3)
3.如图,线段 BD,CE相交于点 A,DE∥BC,若 AB=8,
AD=4,DE=3,则 BC的长为( )
A.3 B.4 C.5 D.6
4.对于二次函数 y= -(x-1)2的图象的特征,下列描述正确的是( )
A.开口向上 B.经过原点 C.对称轴是 y轴 D.顶点在 x轴上
5.如果将抛物线 y x2向上平移 3个单位长度,向左平移 1个单位,得到新的抛物线的
表达式是( )
A. y x 1 2 3 B. y x+1 2 +3 C. y x 1 2 3 D. y x 1 2 +3
6.已知点 A(﹣3,y1),B(2,y2)均在抛物线 y=-2(x﹣1)2+1 上,则下列结论正确
的是( )
A.1<y1<y2 B.1<y2<y1 C.y1<y2<1 D.y2<y1<1
第 1页(共 11页)
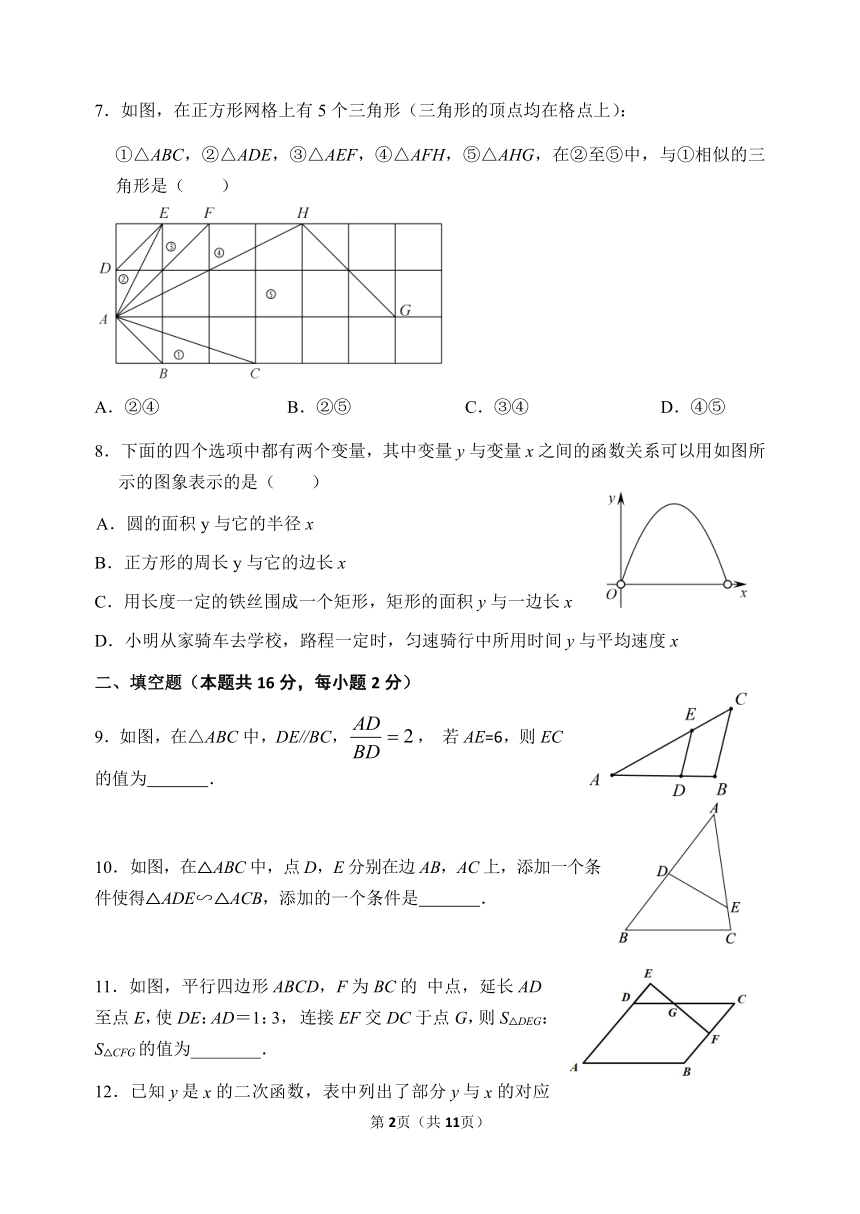
7.如图,在正方形网格上有 5个三角形(三角形的顶点均在格点上):
①△ABC,②△ADE,③△AEF,④△AFH,⑤△AHG,在②至⑤中,与①相似的三
角形是( )
A.②④ B.②⑤ C.③④ D.④⑤
8.下面的四个选项中都有两个变量,其中变量 y与变量 x之间的函数关系可以用如图所
示的图象表示的是( )
A.圆的面积 y与它的半径 x
B.正方形的周长 y与它的边长 x
C.用长度一定的铁丝围成一个矩形,矩形的面积 y与一边长 x
D.小明从家骑车去学校,路程一定时,匀速骑行中所用时间 y与平均速度 x
二、填空题(本题共 16 分,每小题 2 分)
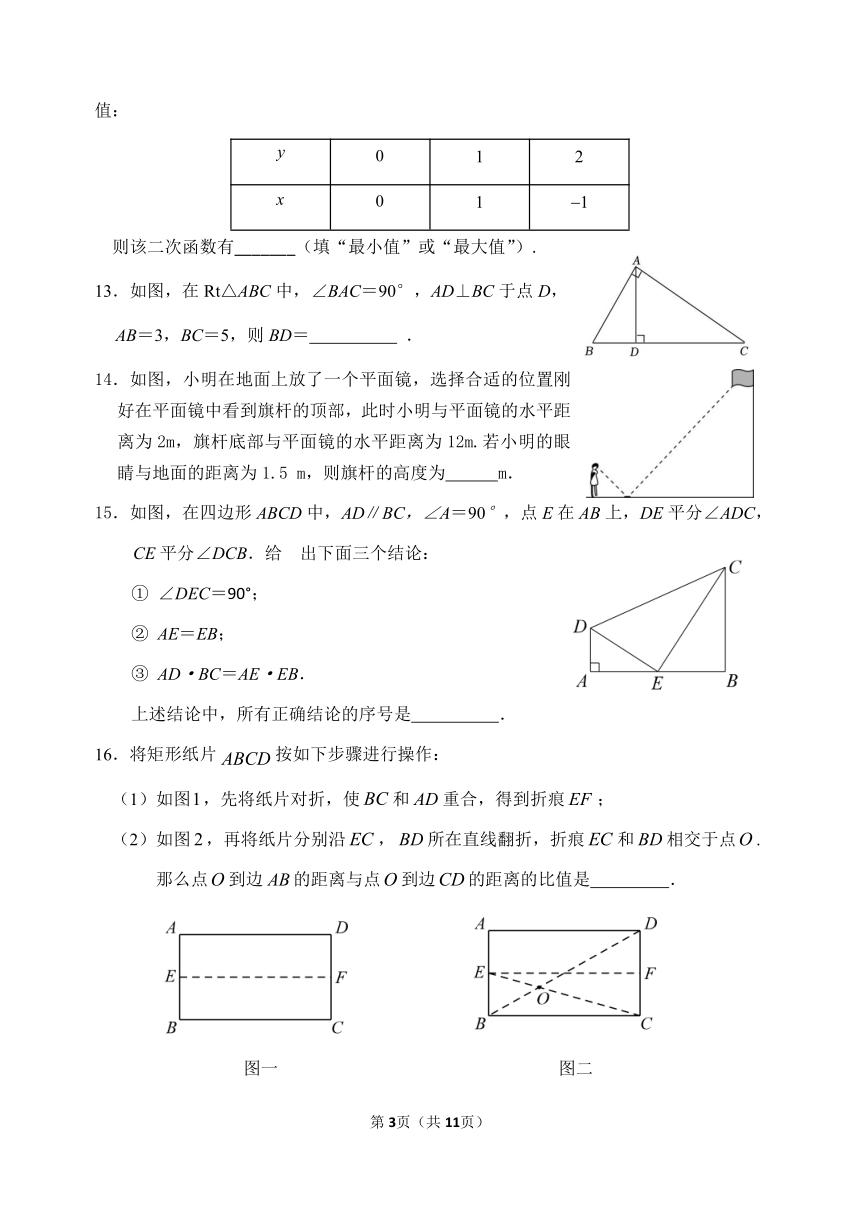
AD
9.如图,在△ABC中,DE//BC, 2, 若 AE=6,则 EC
BD
的值为 .
10.如图,在△ABC中,点D,E分别在边 AB,AC上,添加一个条
件使得△ADE∽△ACB,添加的一个条件是 .
11.如图,平行四边形 ABCD,F为 BC的 中点,延长 AD
至点 E,使 DE:AD=1:3,连接 EF交 DC于点 G,则 S△DEG:
S△CFG的值为________.
12.已知 y是 x的二次函数,表中列出了部分 y与 x的对应
第 2页(共 11页)
值:
y 0 1 2
x 0 1 1
则该二次函数有_______(填“最小值”或“最大值”).
13.如图,在 Rt△ABC中,∠BAC=90°,AD⊥BC于点 D,
AB=3,BC=5,则 BD= .
14.如图,小明在地面上放了一个平面镜,选择合适的位置刚
好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距
离为 2m,旗杆底部与平面镜的水平距离为 12m.若小明的眼
睛与地面的距离为 1.5 m,则旗杆的高度为 m.
15.如图,在四边形 ABCD中,AD∥BC,∠A=90°,点 E在 AB上,DE平分∠ADC,
CE平分∠DCB.给 出下面三个结论:
① ∠DEC=90°;
② AE=EB;
③ AD·BC=AE·EB.
上述结论中,所有正确结论的序号是 .
16.将矩形纸片 ABCD按如下步骤进行操作:
(1)如图1,先将纸片对折,使 BC和 AD重合,得到折痕 EF ;
(2)如图 2,再将纸片分别沿 EC, BD所在直线翻折,折痕 EC和 BD相交于点O .
那么点O到边 AB的距离与点O到边CD的距离的比值是 .
图一 图二
第 3页(共 11页)
三、解答题(本题共 60 分,第 17-23 题每题 5 分,第 24-25 题 6 分,第 26 题 7 分,第
27 题 6 分)解答应写出文字说明,演算步骤或证明过程.
1
17.计算: ( 2)0 2 18 ( ) 1
2
18.解不等式组: 3x 4 2x 1,
5x 3
x. 2
19.已知 x 1是关于 x 的方程 x2 2ax a2 3的一个根,求代数式 a(a 1) a2 5a的
值.
20.如图,在△ABC中,点 D在 AB边上,∠ACD=∠ABC,
求证:(1)△ACD∽△ABC
(2)若 AD=2,AB=5.求 AC的长.
21 1.在平面直角坐标系 xOy中,一次函数 y kx b (k 0)的图象由函数 y x的图象
3
平移得到,且经过点 ( 3, 3) .
(1)求这个一次函数的表达式;
(2)当 x 3时,对于 x的每一个值,函数 y mx (m 0)的值大于函数 y kx b的
值,直接写出m的取值范围.
22.在平面直角坐标系 xOy中,抛物线 y a(x 3)2 1经过点 (2,1).
(1)求该抛物线的表达式;
(2)已知 P( x1,1),Q( x2,1)两点都在该抛物线上,那么 x1 x2 ______ ;
(3)如果点 P(x,y)是此二次函数的图象上一点,若 0≤x≤4 ,则 y的取值范围为_______.
23.为了改善小区环境,某小区决定在一块一边靠墙(墙长 25m)
的空地上修建一个矩形小花园 ABCD,小花园一边靠墙,另三
边用总长 80m 的栅栏围住,如下图所示.若设矩形小花园 AB
边的长为 xm,面积为 ym2.
(1)求 y 与 x之间的函数关系式;
(2)当菜地面积为 600m2时,栅栏的三边长各为多少?
第 4页(共 11页)
24.第二十四届冬季奥林匹克运动会将于 2022年 2 月 4日至 2月 20 日在北京举行,石
景山区作为北京冬奥组委机关驻地和冬奥会滑雪大跳台赛事场地,将迎来作为“双奥之区”
的高光时刻.随着冬奥会的脚步越来越近,石景山教育系统大力普及青少年冰雪运动项
目和知识,越来越多的青少年走向冰场、走进雪场、了解冰雪运动知识.某校在距离冬
奥会开幕倒计时 300 天之际开展了一次冬奥知识答题竞赛,七、八年级各有 200名学生
参加了本次活动,为了解两个年级的答题情况,从两个年级各随机抽取了 20名学生的成
绩进行调查分析,过程如下(数据不完整).
收集数据
七年级 66 70 71 78 71 78 75 78 58 a
63 90 80 85 80 89 85 86 80 87
八年级 61 65 74 70 71 74 74 76 63 b
91 85 80 84 87 83 82 80 86 c
整理、描述数据
七年级成绩统计情况 八年级成绩统计情况
成绩 x/分数
频数 频率 频数 频率
50≤x≤59 1 0.05 0 0
60≤x≤69 2 0.10 3 0.15
70≤x≤79 6 0.30
80≤x≤89 m 10 0.50
90≤x≤100 1 0.05 1 0.05
(说明:成绩 80 分及以上为优秀,60~79 分为合格,60 分以下为不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
年级 平均数 中位数 众数
七年级 77.5 79 80
八年级 77.4 n 74
请根据所给信息,解答下列问题:
(1) a= ,m= ,n= ;
(2)在此次竞赛中,小冬的成绩在七年级能排在前 50%,在八年级只能排在后
50%,那么估计小冬的成绩可能是 ;
(3)估计七年级和八年级此次测试成绩优秀的总人数为 .
第 5页(共 11页)
25. 食用果蔬前,适当浸泡可降低农药的残留.某小组针对同种果蔬研究了不同浸泡方
式对某种农药去除率的影响.
方式一:采用清水浸泡.
记浸泡时间为 t分钟,农药的去除率为 y1%,部分实验数据记录如下:
t(分) 5 8 10 12 15 20
y1(%) 30 50 57 52 37 33
方式二:采用不同浓度的食用碱溶液浸泡相同时间.
记食用碱溶液的浓度为 x%,农药的去除率为 y2%,部分实验数据记录如下:
x(%) 2 5 7 10 12 15
y2(%) 43 52 57 76 57 25
结合实验数据和结果,解决下列问题:
(1)通过分析以上实验数据,发现可以用函数刻画方式一中农药的去除率 y1(%)与浸泡
时间 t(分)之间的关系,方式二中农药的去除率 y2(%)与食用碱溶液的浓度 x(%)之间的关
系,请分别在下面的平面直角坐标系中画出这两个函数的图象:
(2)利用方式一的函数关系可以推断,降低该种农药残留的最佳浸泡时间约
为 分钟.
(3)方式一和方式二的函数关系可以推断,用食用碱溶液浸泡含该种农药的这种果蔬时,
要想不低于清水浸泡的最大去除率,食用碱溶液的浓度 x%中,x 的取值范围可以
是 .
第 6页(共 11页)
26.已知:在平行四边形 ABCD中,AE⊥BC于点 E,DF平分∠ADC,交线段 AE于 F.
(1) 如图 1,若 AE=AD,延长 EA到点 G,使得 AG=BE,连结 DG,依题意补全图形
并证明 DG=AB;
(2) 在(1)的条件下,用等式表示线段 CD,AF,BE之间的数量关系,并证明;
(3) 如图 2,若 AE∶AD=1∶2,用等式表示线段 CD,AF,BE之间的数量关系,直
接写出结果.
第 7页(共 11页)
27.甲、乙、丙三人相约到某游乐园游玩. 该园区在地图上的形状可近似看成等腰直角三
角形,共有三个入口 A,B,C.
图 1 图 2
(1) 园区附近有四个公交车站点,即 1 号、2 号、3 号和 4 号车站. 甲和乙想到园区附
近汇合后一起入园,乙在其中一个站点下车后,两人通过手机共享位置得知甲的位置如
图 1 所示. 两人约定如下:
I. 确定距离自己最近的入口;
II. 如果两人确定的入口相同,则到此入口处汇合并入园;
III. 如果两人确定的入口不同,则到这两个入口的中点处汇合后,再沿逆时针方向绕园区
外围至最近的入口入园.
① 若乙在 4 号车站下车,则甲、乙入园的入口应为 ______________ ;
② 若甲、乙最终在 B 入口处入园,则乙下车的站点可以为______________;
(2)丙从 C 入口先行入园,此时甲、乙还未入园. 丙在地图上建立平面直角坐标系 xOy,
如图 2 所示,其中入口 A,B,C 的坐标分别为(0,4),(-4,0),(4,0). 园区内有行
驶路线为 CG 的摆渡车(乘客可以在路线上任意一点上下车).点 G 坐标为(-3,1). 丙
想乘坐摆渡车和甲、乙汇合,其下车点记为 M,M 到三个入口 A,B,C 的最大距离记为
第 8页(共 11页)
a,到 M 的距离最近的入口记为“理想入口”.
① 如果丙希望在 a 最小处下车,则点 M 的坐标为_______________;
② 若对于摆渡车行驶路线上任意一段长度为 m 的路段,都同时存在“理想入口”分别为
A,B,C 的下车点,则 m的最小值为_______________.
四、附加题(本题共 20 分,每题 5 分)
2 2
28.下列关于二次函数 y (x m) m 1(m为常数)的结论:①该函数的图象与
函数 y x2 的图象形状相同;②该函数的图象一定经过点(0,1);③当 x 0时,y随
x 2的增大而减小;④该函数的图象的顶点在函数 y x 1的图象上,其中所有正确结论
的序号是 .
1 1 1 1 1 1 1 1 1 2 3 4
29. , , ,那么 的值为
x y z 2 y z x 3 z x y 4 x y z
30.在平面直角坐标系 xOy中,矩形 OABC,A(0,3),
B(2,3),C(2,0), 点 M 在边 OA上,OM=1.点 P
在边 AB上运动,连接 PM,点 A 关于直线 PM 的对称
点为 A'. 若 PA=x,MA'+A'B=y, 下列图象能大致反映
y 与 x 的函数关系的是 .
A. B. C. D.
31.如图,在矩形 ABCD中,AB=2BC,点 M是 CD边的中点,点 E ,F分别是边 AB,BC边
上的点,且 AF⊥ME 于点 G,若 EB=2,BF=1,则四边形 BFGE 的面积是 .
第 9页(共 11页)
第 10页(共 11页)
草稿纸
第 11页(共 11页)
数学试卷
(满分 120 分,时间 120 分钟)
班级 姓名 学号 成绩
一、选择题(本题共 24 分,每小题 3 分)
第 1- 8 题均有四个选项,符合题意的选项只有一个.
x 2 y x
1.如果 ,那么 的值是( )
y 3 y
1 1 5 5
A. B. C. D.
3 2 3 2
2.抛物线 y=(x﹣1)2 +3的顶点坐标是( )
A.(1,3) B.(﹣1,3) C.(﹣1,﹣3) D.(1,﹣3)
3.如图,线段 BD,CE相交于点 A,DE∥BC,若 AB=8,
AD=4,DE=3,则 BC的长为( )
A.3 B.4 C.5 D.6
4.对于二次函数 y= -(x-1)2的图象的特征,下列描述正确的是( )
A.开口向上 B.经过原点 C.对称轴是 y轴 D.顶点在 x轴上
5.如果将抛物线 y x2向上平移 3个单位长度,向左平移 1个单位,得到新的抛物线的
表达式是( )
A. y x 1 2 3 B. y x+1 2 +3 C. y x 1 2 3 D. y x 1 2 +3
6.已知点 A(﹣3,y1),B(2,y2)均在抛物线 y=-2(x﹣1)2+1 上,则下列结论正确
的是( )
A.1<y1<y2 B.1<y2<y1 C.y1<y2<1 D.y2<y1<1
第 1页(共 11页)
7.如图,在正方形网格上有 5个三角形(三角形的顶点均在格点上):
①△ABC,②△ADE,③△AEF,④△AFH,⑤△AHG,在②至⑤中,与①相似的三
角形是( )
A.②④ B.②⑤ C.③④ D.④⑤
8.下面的四个选项中都有两个变量,其中变量 y与变量 x之间的函数关系可以用如图所
示的图象表示的是( )
A.圆的面积 y与它的半径 x
B.正方形的周长 y与它的边长 x
C.用长度一定的铁丝围成一个矩形,矩形的面积 y与一边长 x
D.小明从家骑车去学校,路程一定时,匀速骑行中所用时间 y与平均速度 x
二、填空题(本题共 16 分,每小题 2 分)
AD
9.如图,在△ABC中,DE//BC, 2, 若 AE=6,则 EC
BD
的值为 .
10.如图,在△ABC中,点D,E分别在边 AB,AC上,添加一个条
件使得△ADE∽△ACB,添加的一个条件是 .
11.如图,平行四边形 ABCD,F为 BC的 中点,延长 AD
至点 E,使 DE:AD=1:3,连接 EF交 DC于点 G,则 S△DEG:
S△CFG的值为________.
12.已知 y是 x的二次函数,表中列出了部分 y与 x的对应
第 2页(共 11页)
值:
y 0 1 2
x 0 1 1
则该二次函数有_______(填“最小值”或“最大值”).
13.如图,在 Rt△ABC中,∠BAC=90°,AD⊥BC于点 D,
AB=3,BC=5,则 BD= .
14.如图,小明在地面上放了一个平面镜,选择合适的位置刚
好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距
离为 2m,旗杆底部与平面镜的水平距离为 12m.若小明的眼
睛与地面的距离为 1.5 m,则旗杆的高度为 m.
15.如图,在四边形 ABCD中,AD∥BC,∠A=90°,点 E在 AB上,DE平分∠ADC,
CE平分∠DCB.给 出下面三个结论:
① ∠DEC=90°;
② AE=EB;
③ AD·BC=AE·EB.
上述结论中,所有正确结论的序号是 .
16.将矩形纸片 ABCD按如下步骤进行操作:
(1)如图1,先将纸片对折,使 BC和 AD重合,得到折痕 EF ;
(2)如图 2,再将纸片分别沿 EC, BD所在直线翻折,折痕 EC和 BD相交于点O .
那么点O到边 AB的距离与点O到边CD的距离的比值是 .
图一 图二
第 3页(共 11页)
三、解答题(本题共 60 分,第 17-23 题每题 5 分,第 24-25 题 6 分,第 26 题 7 分,第
27 题 6 分)解答应写出文字说明,演算步骤或证明过程.
1
17.计算: ( 2)0 2 18 ( ) 1
2
18.解不等式组: 3x 4 2x 1,
5x 3
x. 2
19.已知 x 1是关于 x 的方程 x2 2ax a2 3的一个根,求代数式 a(a 1) a2 5a的
值.
20.如图,在△ABC中,点 D在 AB边上,∠ACD=∠ABC,
求证:(1)△ACD∽△ABC
(2)若 AD=2,AB=5.求 AC的长.
21 1.在平面直角坐标系 xOy中,一次函数 y kx b (k 0)的图象由函数 y x的图象
3
平移得到,且经过点 ( 3, 3) .
(1)求这个一次函数的表达式;
(2)当 x 3时,对于 x的每一个值,函数 y mx (m 0)的值大于函数 y kx b的
值,直接写出m的取值范围.
22.在平面直角坐标系 xOy中,抛物线 y a(x 3)2 1经过点 (2,1).
(1)求该抛物线的表达式;
(2)已知 P( x1,1),Q( x2,1)两点都在该抛物线上,那么 x1 x2 ______ ;
(3)如果点 P(x,y)是此二次函数的图象上一点,若 0≤x≤4 ,则 y的取值范围为_______.
23.为了改善小区环境,某小区决定在一块一边靠墙(墙长 25m)
的空地上修建一个矩形小花园 ABCD,小花园一边靠墙,另三
边用总长 80m 的栅栏围住,如下图所示.若设矩形小花园 AB
边的长为 xm,面积为 ym2.
(1)求 y 与 x之间的函数关系式;
(2)当菜地面积为 600m2时,栅栏的三边长各为多少?
第 4页(共 11页)
24.第二十四届冬季奥林匹克运动会将于 2022年 2 月 4日至 2月 20 日在北京举行,石
景山区作为北京冬奥组委机关驻地和冬奥会滑雪大跳台赛事场地,将迎来作为“双奥之区”
的高光时刻.随着冬奥会的脚步越来越近,石景山教育系统大力普及青少年冰雪运动项
目和知识,越来越多的青少年走向冰场、走进雪场、了解冰雪运动知识.某校在距离冬
奥会开幕倒计时 300 天之际开展了一次冬奥知识答题竞赛,七、八年级各有 200名学生
参加了本次活动,为了解两个年级的答题情况,从两个年级各随机抽取了 20名学生的成
绩进行调查分析,过程如下(数据不完整).
收集数据
七年级 66 70 71 78 71 78 75 78 58 a
63 90 80 85 80 89 85 86 80 87
八年级 61 65 74 70 71 74 74 76 63 b
91 85 80 84 87 83 82 80 86 c
整理、描述数据
七年级成绩统计情况 八年级成绩统计情况
成绩 x/分数
频数 频率 频数 频率
50≤x≤59 1 0.05 0 0
60≤x≤69 2 0.10 3 0.15
70≤x≤79 6 0.30
80≤x≤89 m 10 0.50
90≤x≤100 1 0.05 1 0.05
(说明:成绩 80 分及以上为优秀,60~79 分为合格,60 分以下为不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
年级 平均数 中位数 众数
七年级 77.5 79 80
八年级 77.4 n 74
请根据所给信息,解答下列问题:
(1) a= ,m= ,n= ;
(2)在此次竞赛中,小冬的成绩在七年级能排在前 50%,在八年级只能排在后
50%,那么估计小冬的成绩可能是 ;
(3)估计七年级和八年级此次测试成绩优秀的总人数为 .
第 5页(共 11页)
25. 食用果蔬前,适当浸泡可降低农药的残留.某小组针对同种果蔬研究了不同浸泡方
式对某种农药去除率的影响.
方式一:采用清水浸泡.
记浸泡时间为 t分钟,农药的去除率为 y1%,部分实验数据记录如下:
t(分) 5 8 10 12 15 20
y1(%) 30 50 57 52 37 33
方式二:采用不同浓度的食用碱溶液浸泡相同时间.
记食用碱溶液的浓度为 x%,农药的去除率为 y2%,部分实验数据记录如下:
x(%) 2 5 7 10 12 15
y2(%) 43 52 57 76 57 25
结合实验数据和结果,解决下列问题:
(1)通过分析以上实验数据,发现可以用函数刻画方式一中农药的去除率 y1(%)与浸泡
时间 t(分)之间的关系,方式二中农药的去除率 y2(%)与食用碱溶液的浓度 x(%)之间的关
系,请分别在下面的平面直角坐标系中画出这两个函数的图象:
(2)利用方式一的函数关系可以推断,降低该种农药残留的最佳浸泡时间约
为 分钟.
(3)方式一和方式二的函数关系可以推断,用食用碱溶液浸泡含该种农药的这种果蔬时,
要想不低于清水浸泡的最大去除率,食用碱溶液的浓度 x%中,x 的取值范围可以
是 .
第 6页(共 11页)
26.已知:在平行四边形 ABCD中,AE⊥BC于点 E,DF平分∠ADC,交线段 AE于 F.
(1) 如图 1,若 AE=AD,延长 EA到点 G,使得 AG=BE,连结 DG,依题意补全图形
并证明 DG=AB;
(2) 在(1)的条件下,用等式表示线段 CD,AF,BE之间的数量关系,并证明;
(3) 如图 2,若 AE∶AD=1∶2,用等式表示线段 CD,AF,BE之间的数量关系,直
接写出结果.
第 7页(共 11页)
27.甲、乙、丙三人相约到某游乐园游玩. 该园区在地图上的形状可近似看成等腰直角三
角形,共有三个入口 A,B,C.
图 1 图 2
(1) 园区附近有四个公交车站点,即 1 号、2 号、3 号和 4 号车站. 甲和乙想到园区附
近汇合后一起入园,乙在其中一个站点下车后,两人通过手机共享位置得知甲的位置如
图 1 所示. 两人约定如下:
I. 确定距离自己最近的入口;
II. 如果两人确定的入口相同,则到此入口处汇合并入园;
III. 如果两人确定的入口不同,则到这两个入口的中点处汇合后,再沿逆时针方向绕园区
外围至最近的入口入园.
① 若乙在 4 号车站下车,则甲、乙入园的入口应为 ______________ ;
② 若甲、乙最终在 B 入口处入园,则乙下车的站点可以为______________;
(2)丙从 C 入口先行入园,此时甲、乙还未入园. 丙在地图上建立平面直角坐标系 xOy,
如图 2 所示,其中入口 A,B,C 的坐标分别为(0,4),(-4,0),(4,0). 园区内有行
驶路线为 CG 的摆渡车(乘客可以在路线上任意一点上下车).点 G 坐标为(-3,1). 丙
想乘坐摆渡车和甲、乙汇合,其下车点记为 M,M 到三个入口 A,B,C 的最大距离记为
第 8页(共 11页)
a,到 M 的距离最近的入口记为“理想入口”.
① 如果丙希望在 a 最小处下车,则点 M 的坐标为_______________;
② 若对于摆渡车行驶路线上任意一段长度为 m 的路段,都同时存在“理想入口”分别为
A,B,C 的下车点,则 m的最小值为_______________.
四、附加题(本题共 20 分,每题 5 分)
2 2
28.下列关于二次函数 y (x m) m 1(m为常数)的结论:①该函数的图象与
函数 y x2 的图象形状相同;②该函数的图象一定经过点(0,1);③当 x 0时,y随
x 2的增大而减小;④该函数的图象的顶点在函数 y x 1的图象上,其中所有正确结论
的序号是 .
1 1 1 1 1 1 1 1 1 2 3 4
29. , , ,那么 的值为
x y z 2 y z x 3 z x y 4 x y z
30.在平面直角坐标系 xOy中,矩形 OABC,A(0,3),
B(2,3),C(2,0), 点 M 在边 OA上,OM=1.点 P
在边 AB上运动,连接 PM,点 A 关于直线 PM 的对称
点为 A'. 若 PA=x,MA'+A'B=y, 下列图象能大致反映
y 与 x 的函数关系的是 .
A. B. C. D.
31.如图,在矩形 ABCD中,AB=2BC,点 M是 CD边的中点,点 E ,F分别是边 AB,BC边
上的点,且 AF⊥ME 于点 G,若 EB=2,BF=1,则四边形 BFGE 的面积是 .
第 9页(共 11页)
第 10页(共 11页)
草稿纸
第 11页(共 11页)
同课章节目录
